基于等离子体的GTS模型气动减阻研究

王靖宇 周申申 胡兴军 惠政

摘   要：为探究等离子体对类厢式货车的气动减阻效果，以GTS模型为研究对象，采用数值仿真的方法，分别研究了当来流风速为20 m/s时，3个位置处等离子体布置角度、激励电压对GTS模型的气动减阻效果并分析其减阻机理，然后进行组合工况的分析. 研究结果表明，等离子体是通过诱导近壁面气体定向流动使流动分离点后移、推迟流动的分离，从而减小GTS模型前后压差阻力、降低整车气动阻力系数，等离子体布置的位置在流动分离点后方并且靠近流动分离点. 单个位置激励时，等离子体布置在GTS尾部两侧时气动减阻效果最好，最大减阻率为5.09%;组合工况时最大减阻率可达6.01%. 当来流风速一定时，等离子体存在最佳布置角度与激励电压.

关键词：等离子体;激励电压;地面运输系统模型;汽车空气动力学;主动流动控制;车辆工程

Abstract：In order to study the aerodynamic drag reduction effect of the plasma on kind of vans， ground transportation system（GTS） model was taken as the research object. Numerical simulation was used to investigate the aerodynamic drag reduction effect of plasma arrangement angle and excitation voltage at three positions on the GTS model when the incoming wind speed was 20 m/s，and the drag reduction mechanism was analyzed. Then， the combined working conditions were analyzed. The results show that plasma can make the separation point of the flow move back and delay the separation of the flow by inducing the directional flow of gas near the wall， so as to reduce the pressure difference between the front and rear of the GTS model and reduce the aerodynamic drag coefficient of the vehicle. Moreover， plasma should be set behind and close to the flow separation point. The aerodynamic drag reduction effect is the best when plasma is applied to both sides of the tail of GTS at a single position， and the maximum drag reduction rate is 5.09%. The maximum drag reduction rate can reach 6.01% under combined condition. When the incoming wind velocity is constant， the plasma has the optimal arrangement angle and excitation voltage.

Key words：plasma;excitation voltage;Ground Transportation System（GTS） model;automobile aerodynamics;active flow control;vehicle engineering

隨着能源问题的日益严峻、燃油价格的不断上涨，如何进一步降低汽车的气动阻力问题已成为研究热点[1]. 厢式货车车身流线型差，气动阻力系数较大，一般为0.6～0.7;当车速达到90 km/h时，发动机功率的80%将用于克服空气阻力[2]. 因此降低厢式货车的气动阻力对于节能减排具有重要意义.

王靖宇等人[3]采用数值模拟的方法，在厢式货车前部加装导流罩，将整车气动阻力降低10%以上;杨小龙等人[4]通过采用尾部上翘角减小货车尾部分离区强度，当上翘角在10°时，整车气动阻力系数降低约6%.

在过去的几年中，主动流动控制概念已经成为流体力学中越来越重要的课题. 等离子体流动控制技术具有结构简单、能耗低、动态响应快等优点[5-6]，受到相关学者的关注与研究.

王靖宇等人[7]应用等离子体对后台阶流动的尾流场进行主动控制，将再附着位置提前45.27%;李正农等人[8]采用数值模拟与风洞试验相结合的方法，对低矮房屋平屋面进行等离子体流动控制，改善屋面的局部风压系数的大小及分布，提高建筑结构抗风能力.

目前对等离子体流动控制的研究多集中在航空领域[9-12]，而本文将等离子体应用到汽车领域. 首先对由美国Sandia国家实验室提出的类厢式货车地面运输系统（GTS）模型进行外流场仿真，分析整车气动阻力系数较大的原因;然后以流场信息为指导布置等离子体的位置，揭示等离子体对流场控制的机理，并探究等离子体最佳布置角度与激励电压及其对应的气动减阻效果. 本文研究结果可对等离子体在汽车上的应用提供参考.

1   等离子体气动激励及能耗分析

1.1   等离子体气动激励

等离子体是除了液态、固态以及气态之外的物质存在第四态.[13] 介质阻挡放电（Dielectric Barrier Discharge，DBD）是產生稳定低温等离子体的有效方法，其基本结构如图1所示.

一方面，在高压电源的作用下，上电极附近空气被电离成电子和离子共同存在的等离子体状态，在电场的作用下，正离子向负极板（下电极）定向运动，伴随着与部分空气分子发生碰撞，整体表现为诱导壁面附近气体向右定向移动;另一方面，等离子体放电过程中也会产生局部温度和压力变化而引发温升及脉冲效应. 二者的共同作用实现等离子体对流场的主动干扰.

1.2   等离子体数值仿真验证

对于介质阻挡放电等离子体模型，采用由Shyy等人[14]提出的等离子体对流场作用方程的简化模型，综合考虑等离子体激励电压、频率、极板几何形状等因素，将试验工况时等离子体的流动控制效果写成如下方程：

选用三维长方体空腔模型进行等离子体数值仿真的验证，将地面作为等离子体布置位置，其几何模型纵向中截面如图2所示. 由于等离子体的产生及在电磁场作用下的运动核心区域大小为3 mm×1.5 mm，因此在产生等离子体处需对网格进行加密，本文在该处最小尺寸取0.1 mm，使该区域内有足够的网格数，以呈现等离子体诱导风速随远离电极板而衰减的趋势. 仿真边界条件如表1所示.

由于等离子体核心作用区域大部分处于边界层内部，故为准确描述等离子体对近壁面流动的控制效果，选取湍流模型为SST k-ω. 经计算得到2 m/s来流风速时纵向中截面仿真速度云图如图3所示.

由图3可以看出，布置等离子体的效果为对近壁面附近空气诱导出水平向右、具有一定速度的气流，并且在等离子体布置位置处诱导速度最大;随着流动向后发展，速度值逐渐衰减. 为检验仿真结果的准确性，在等离子体布置位置右侧3.8 mm处，作垂直于地面纵向中线的一条线，如图2所示虚线AB. 监测各来流风速下此虚线上沿y轴的速度分布，并将本文仿真结果与文献[14]仿真结果进行对比，结果如图4所示.

图4中，u为虚线AB上速度值;V∞为自由来流速度. 由图4可以看出，本文的仿真结果与文献[14]仿真结果基本一致，且各来流风速下诱导最大风速的误差小于3%，由此验证本文对等离子体仿真的准确性.

1.3   能耗分析

等离子体是通过能量的输入改变流动边界层的特性来实现主动流动控制，因此，存在成本与收益问题，这就是等离子体是否具有实用价值的关键所在. 傅鑫[15]以试验研究为手段，探究等离子体消耗电功率与其各放电参数间的相互关系，并得到极板间水平距离为2 mm、激励频率为3 kHz、激励电压小于8 kV时（与文献[14]一致），等离子体消耗功率不超过3 W.

由此可以看出，虽然为获得低温等离子体所需激励电压较高，但其电流值仅为电子撞击上电极的累积效果，因此该值较小，故所消耗功率较小. 消耗电能与气动阻力系数减小量之间的关系为：

2   GTS模型外流场仿真分析

本文所选厢式货车模型为1/14 GTS模型，根据其标准尺寸[16]，建立几何模型如图5所示.

在ICEM-CFD软件中进行计算域的选取及相应网格的划分. GTS模型特征长度L = 0.2 m，取GTS头部到计算域前端为4L，尾部距计算域出口为7L，车身左右距计算域两侧各5L，上部距计算域顶端为6L，由此得到GTS的阻塞比小于1%，利于流动充分发展.

对模型进行相应的网格划分，整体采用三棱柱加四面体的混合网格方案. 经网格无关性验证后发现，GTS车身表面最大网格尺寸取10 mm即可达到仿真精度要求. 为准确计算边界层内部的流动，取第1层网格到圆柱表面量纲化的距离y+=1，在边界层网格划分时，基层厚度取0.015 mm，共15层，由此得到总厚度为0.72 mm的边界层. 整体网格情况如图6所示.

在上述网格方案的基础上，采用双精度的计算方法在Fluent软件中迭代计算. 仿真边界条件如表2所示.

为准确计算边界层内部的流动状态，湍流模型选择SST k-ω. 经迭代后计算结果显示，GTS整车气动阻力系数为0.492 5，与现有试验值[17]误差小于2%，由此验证本文对GTS模型仿真的准确性. 作沿x方向纵向中截面速度矢量图及GTS模型头部压力云图如图7所示.

由图7可以看出，GTS头部两侧出现流动的分离、其尾部后方存在较大面积的负压区，这导致GTS前后压差阻力较大，从而整车气动阻力较大. 因此考虑在GTS头部和尾部流动分离区域布置等离子体来降低整车气动阻力系数. 等离子体具体待布置位置如图8所示，位置1为GTS尾部上方，位置2为尾部左右两侧，位置3为头部竖向两侧.

3   等离子体对GTS模型减阻效果研究

为方便等离子体的布置及改变等离子体流动控制方向，同时尽可能多位置布置等离子体以及考虑到厢式货车装卸货的方便性，对GTS模型尾部上方及左右两侧进行倒圆改型，倒圆半径r=30 mm，下部保持其原有的形状. 改型后的GTS尾部形状如图9所示.

采用与改型前相同的网格策略及数值模拟设置方案对改型后的GTS模型进行仿真，并将此状态作为基础工况. 经迭代计算后得到改型后GTS整车气动阻力系数Cd为0.445 8. 这与改型前的0.492 5相比降低了9.48%.

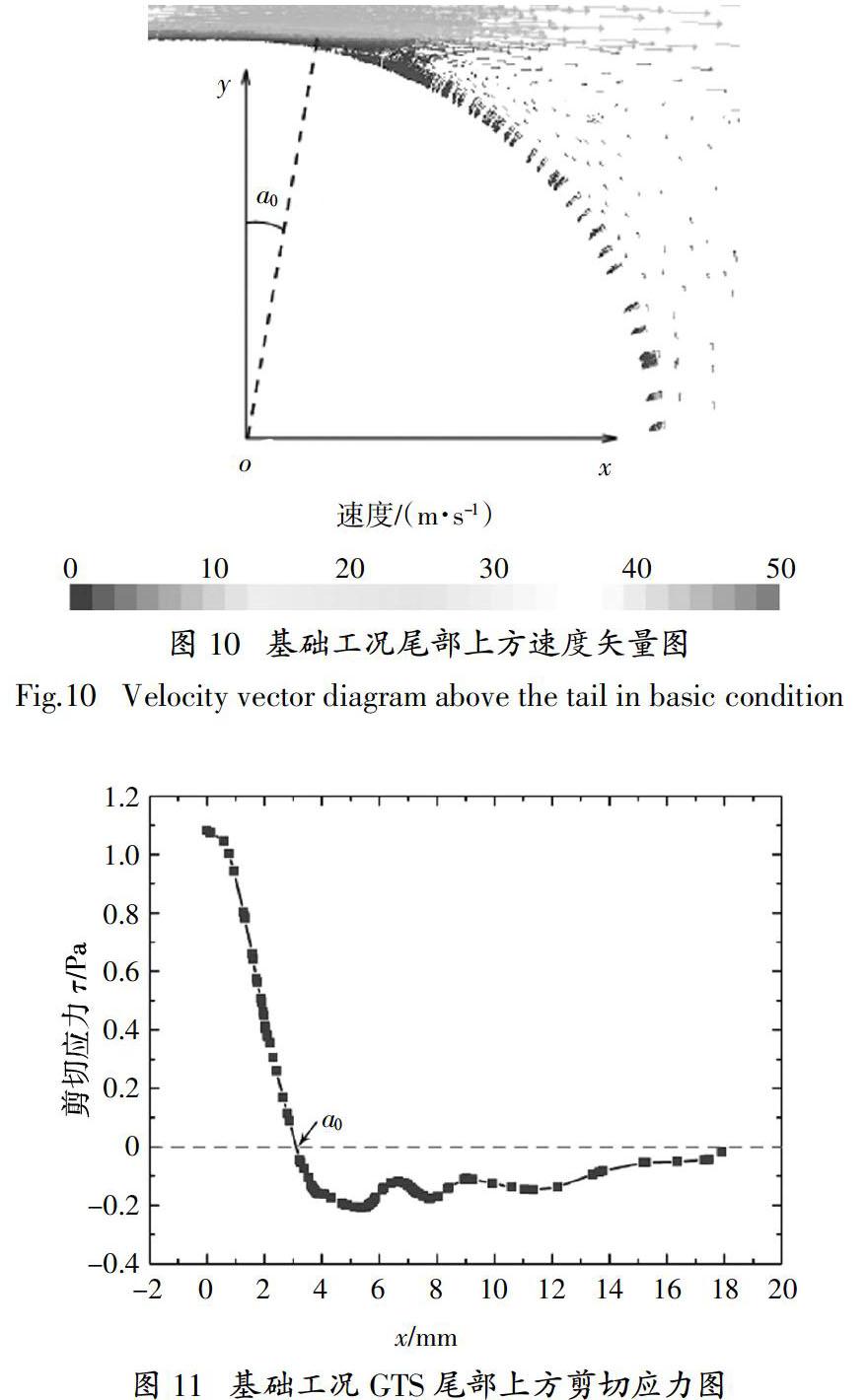
改型后沿x方向基础工况尾部上方速度矢量图和基础工况GTS模型尾部上方剪切应力图分别如图10和图11所示. 由此计算得到基础工况时GTS模型尾部上方流动分离点为a0 = 9.92°.

3.1   位置1处等离子体不同布置角度对GTS模型气动减阻效果

在分离点后部选取a分别为10°、15°、20°、25°、30° 5个等离子体待布置角度，具体位置如图12所示. 由于等离子体的产生及在电磁场作用下運动的核心区域大小为3 mm×1.5 mm，因此在产生等离子体处需对网格进行加密，本文在该处最小尺寸取0.1 mm，使该区域内有足够的网格数，以呈现离子与空气分子作用的体积力随远离电极板而衰减的趋势，其余网格方案与基础工况保持一致. 由此得到的尾部网格方案如图13所示. 在上述网格方案的基础上，采用双精度的计算方法在Fluent软件中迭代计算. 边界条件的设置与基础工况保持一致，将等离子体激励电压改为5 kV，其余与文献[14]保持一致. 计算得到等离子体布置角度与GTS整车气动阻力系数关系如图14所示.

由图14可以看出，随着等离子体布置角度的增大，GTS模型气动阻力系数先减小后增大;并且当在15°处布置等离子体时，整车气动阻力系数最小，仅为0.428 0，与将尾部倒圆时的基础工况0.445 8相比，气动阻力系数降低了3.99%. 在各角度布置等离子体激励时，GTS模型气动阻力系数减小量ΔCd大于0.008 7，可以看出等离子体气动减阻效果远大于其电能消耗.

对比基础工况与在15°布置等离子体时，沿x方向GTS尾部上方基础工况与等离子体激励最佳工况局部速度矢量对比图和GTS尾部上方最佳工况与基础工况剪切应力对比图分别如图15和图16所示.

由图15可以看出，布置等离子体激励后，等离子体诱导近壁面气体定向移动，与初始流动进行耦合，使GTS尾部上方气体流动速度明显增大，且流动分离角度由a0增加至a1;结合剪切应力图计算得出，布置等离子体后流动分离点为a1 = 17.95°，与基础工况的a0 = 9.92°相比后移8.03°. 由此可见，等离子体对GTS模型流动控制机理为通过诱导近壁面气体定向移动来推迟GTS尾部上方流动的分离，使流动分离点后移，从而降低车身尾部负压区大小，降低车身前后压差阻力，降低整车气动阻力系数.

但随着等离子体布置角度的进一步增加，整车气动阻力系数反而升高. a = 30°与基础工况沿x方向GTS尾部中截面剪切应力对比如图17所示.

由图17可以看出，在30°布置等离子体时，尽管等离子体作用区域部分剪切应力为正，但在等离子体作用位置前部仍有较大范围的负压区，说明此时等离子体作用区域完全处于GTS尾部的湍流核心区内部;该工况虽然也可将流动分离点a0向后推移，但与在15°布置等离子体相比减阻效果降低. 由此可见，等离子体的布置位置要在流动分离点后方附近而不能过于远离分离点，使布置等离子体激励后负压区均在等离子体作用区域的后部，这样才能产生最佳气动减阻效果.

3.2   位置1处不同激励电压对GTS模型气动减阻效果

改变等离子体激励电压，进一步研究在位置1处不同激励电压对GTS的减阻效果的影响. 等离子体激励电压分别调整为3、4、5、6、7 kV，网格方案及数值模拟仿真方案均与3.1节相同，并在各激励电压下研究等离子体布置角度与GTS整车气动阻力系数的关系. 限于篇幅，这里仅列出各激励电压下，等离子体最佳布置角度时整车气动阻力系数，如表3所示.

由表3整理得到在各激励电压、最佳布置角度时，GTS整车气动阻力系数如图18所示.

由图18可以看出，当来流风速为20 m/s，等离子体激励电压在5 kV左右时，等离子体对GTS整车气动阻力系数均有一定程度的减小;当激励电压小于5 kV时，随着激励电压的升高，等离子体对GTS气动减阻效果增强;但激励电压超过5 kV时，等离子体的减阻效果减弱. 激励电压分别为5 kV和7 kV时GTS尾部湍流动能云图如图19所示.

由图19可以看出，随着激励电压的进一步增加，等离子体诱导空气定向移动的速度增加，使GTS尾部湍流强度增强，从而整车气动阻力系数略微增高. 由此可见，当来流风速一定时，等离子体对GTS模型气动阻力系数的降低存在最佳激励电压.

3.3   位置2处等离子体不同布置角度对GTS模型气动减阻效果

与在GTS尾部上方布置等离子体激励的方法类似，在其尾部两侧、分离点后部选取a分别为10°、15°、20°、25°、30° 5个等离子体待布置位置. GTS尾部两侧加密后网格方案如图20所示. 采用双精度的计算方法在Fluent软件中迭代计算. 边界条件的设置与基础工况保持一致，等离子体激励电压取5 kV，通过计算得到等离子体布置角度与GTS整车气动阻力系数关系如图21所示.

由图21可以看出，当在GTS尾部两侧15°处布置等离子体时为最佳工况，整车气动阻力系数仅为0.423 3，与基础工况的0.445 8相比，降低了5.09%. 且当等离子体布置在最佳激励位置15°附近时，均有较好的减阻效果. 对比基础工况与在15°布置等离子体时，GTS模型尾部两侧基础工况与最佳工况x方向速度云图如图22所示.

由图22可见，在15°位置布置等离子体激励时，GTS模型尾部负压区大小及强度明显减小，从而整车前后压差阻力较小，整车气动阻力系数较低.

与在GTS尾部上方布置等离子体激励相似的是，当等离子体布置在30°位置时，整车气动阻力为0.463 7，这与基础工况相比反而增加了4.02%. 对比基础工况与激励角度为30°时，沿x方向GTS尾部横向中截面剪切应力对比如图23所示.

由图23可以看出，等离子体作用区域之前也出现了部分负压区，此时等离子体作用区域整体处于尾部湍流核心区内部. 并且由图20所示工况计算得出：基础工况时，GTS尾部左右两侧流动分离点为a0 = 9.92°;在30°布置5 kV激励时，流动分离点为a1 = 8.96°;说明此时由于等离子体处于湍流核心区内部，其作用效果反而使流动分离点进一步前移，GTS尾部湍流区域进一步增大，从而整车气动阻力系数升高.

进一步说明等离子体的位置需要布置在流动分离点后方附近，从而推迟流动的分离，降低整车气动阻力;但不能过于远离流动分离点，这样会使等离子体的作用区域整体处于分离区内部，降低等离子体气动减阻能力，甚至增加整车气动阻力系数.

3.4   位置2处不同激励电压对GTS模型气动减阻效果

调整等离子体激励电压U分别为3、4、5、6 kV，分别在各激励电压下研究等离子体布置角度与GTS整车气动阻力系数的关系. 这里也仅列出各激励电压下，等离子体最佳布置角度时整车气动阻力系数，结果如表4所示. 由表4整理得到各激励电压下、最佳作用角度时激励电压与GTS整车气动阻力系数关系，如图24所示. 由图24可以看出，当来流风速为20 m/s，等离子体激励电压为4 kV时，等离子体对GTS整车气动减阻效果最好，对应的减阻率为5.18%;激励电压在4 kV附近时，等离子体对GTS均有较好的减阻效果;但激励电压超过5 kV时，GTS模型气动阻力系数增加.

3.5   位置3处不同激励电压对GTS模型气动减阻效果

在GTS头部等离子体待布置位置进行网格的加密，最小网格尺寸取0.1 mm，其余网格方案不变. 加密后GTS头部网格方案如图25所示. 与前文计算方法一致，经过计算得到在位置3处等离子体激励电压与GTS整车气动阻力系数Cd关系如图26所示.

由图26可以看出，当激励电压U = 3 kV时，整车气动阻力系数最低，为0.425 5，与基础工况相比减阻4.55%. 基础工况与等离子体最佳激励电压时GTS头部压力云图如图27所示.

由图27可以看出，等离子体在GTS头部两侧推迟流动的分离，减小头部两侧负压区大小，进而降低整车气动阻力系数. 当激励电压略大于3 kV时，均有不同程度的减阻效果;但当激励电压小于3 kV时，由于等离子体激励能量较小，其控制结果并没有将流动分离点推迟至控制区域后方，而是其作用区域整体处于流动分离区内部，这样反而增大分离区大小，增加整车气动阻力系数.

4   组合工况时等离子体对GTS模型的减阻效果

由于GTS头部离尾部较远，对尾部流动情况影响较小;尾部上方与左右两侧流动方向相互垂直，经预试验发现二者相互干扰也较小. 那么在20 m/s的来流风速下，分别取上文所述3個位置的最佳减阻工况进行组合计算，即对于位置1，在a = 15°处布置等离子体，激励电压U = 5 kV;对于位置2，在a = 15°处布置等离子体，激励电压U = 4 kV;位置3处等离子体激励电压取U = 3 kV. 由此仿真得到等离子体对GTS组合工况的减阻效果，结果如表5所示. 由表5可以看出，各位置组合工况均有较好的减阻效果;对于在两个位置布置等离子体激励来讲，在各来流风速下，位置1与位置3的组合方案比另两种组合方案气动减阻效果更优;且当3个位置的最优工况进行组合时，整车气动阻力系数为0.419 0，与基础工况相比减阻率达6.01%.

5   结   论

本文应用Fluent软件，探究等离子体对类厢式货车GTS模型的气动减阻效果. 首先探究单独位置处、不同激励电压下等离子体的最佳布置位置及其气动减阻效果，并揭示等离子体对流场控制的机理;然后探究组合工况时等离子体的气动减阻效果. 通过研究得到以下结论：

1）等离子体对GTS模型流动控制机理是通过诱导近壁面气体定向流动来推迟流动的分离、使流动分离点后移，降低车身尾部负压区大小，降低车身前后压差阻力从而降低整车气动阻力系数.

2）等离子体的布置位置应在流动分离点后部并且靠近流动分离点，这样等离子体才能起到推迟流动分离的作用，进而降低整车气动阻力系数;如果过于远离流动分离点，会降低等离子体流动控制的效果，甚至增大整车气动阻力系数.

3）随着等离子体激励电压的增加，等离子体对流场控制效果增强;但激励电压过大，会使激励位置后部湍流强度增加，使等离子体的气动减阻效果减弱.

4）当来流风速一定时，等离子体存在最佳激励电压与作用角度;且单个位置激励时，等离子体布置在GTS尾部两侧时气动减阻效果最好，最大减阻率为5.09%;组合工况时最大减阻率可达6.01%.

参考文献

[1]    张英朝，曹惠南，朱会. MIRA阶背式模型的瞬态流动结构分析[J]. 湖南大学学报（自然科学版），2019，46（8）：51—58.

ZHANG Y C，CAO H N，ZHU H. Instantaneous flow structure analysis of MIRA notchback model[J]. Journal of Hunan University（Natural Sciences），2019，46（8）：51—58. （In Chinese）

[2]    PATEL N，HE M，HEMIDA H，et al. Large-eddy simulation of the airflow around a truck[J]. Journal of Wind Engineering and Industrial Aerodynamics，2019，195：104017.

[3]    王靖宇，胡兴军，田华，等. 导流罩对轻型厢式货车气动特性影响的数值模拟[J]. 吉林大学学报（工学版），2008，38（1）：14—18.

WANG J Y，HU X J，TIAN H，et al. Numerical simulation of influence of guide cowl on light-duty van aerodynamic characteristics[J]. Journal of Jilin University（Engineering and Technology Edition），2008，38（1）：14—18. （In Chinese）

[4]    杨小龙，胡凯耀. 一种厢式货车被动减阻技术研究[J]. 湖南大学学报（自然科学版），2012，39（3）：33—37.

YANG X L，HU K Y. Study of a passive drag reduction technology for trucks[J]. Journal of Hunan University（Natural Sciences），2012，39（3）：33—37.（In Chinese）

[5]    BOEUF J P，PITCHFORD L C. Electrohydrodynamic force and aerodynamic flow acceleration in surface dielectric barrier discharge[J]. Journal of Applied Physics，2005，97（10）：103307—103316.

[6]    JEYANGEL A S S，JANCIRANI J. Experimental investigation and ANN prediction on the underbody drag minimization in truck model using DC pulsed DBD plasma actuator as an active flow control device[J]. Journal of Applied Fluid Mechanics，2019，12（1）：195—205.

[7]    王靖宇，周申申，胡兴军. 等离子体控制下后台阶流动的数值模拟[J]. 重庆理工大学学报（自然科学版），2019，33（2）：56—61.

WANG J Y，ZHOU S S，HU X J. Numerical simulation of backward-facing step flow controlled by plasma [J]. Journal of Chongqing Institute of Technology（Natural Sciences），2019，33（2）：56—61.（In Chinese）

[8]    李正农，王鹏，张学文. 等离子体流动控制试验与仿真对比研究[J]. 湖南大学学报（自然科学版），2019，46（7）：86—95.

LI Z N，WANG P，ZHANG X W. Comparative study of experiment and simulation on plasma flow control [J]. Journal of Hunan University （Natural Sciences），2019，46（7）：86—95. （In Chinese）

[9]    JAYARAMAN B，THAKUR S，SHYY W. Modeling of fluid dynamics and heat transfer induced by dielectric barrier plasma actuator [J]. Journal of Heat Transfer，2007，129 （4）：517—525.

[10]  姚軍锴，何海波，周丹杰，等. 等离子体激励对飞翼布局飞行器增升及流态影响[J]. 西北工业大学学报，2018，36（5）：963—969.

YAO J K，HE H B，ZHOU D J，et al. Effects of plasma actuator discharge on lift-enhancement and flow patterns of flying wing aircraft[J]. Journal of Northwestern Polytechnical University，2018，36（5）：963—969. （In Chinese）

[11]  ROY S，GAITONDE D V. Force interaction of high pressure glow discharge with fluid flow for active separation control[J]. Physics of Plasmas，2006，13（2）：23503—23513.

[12]  龙玥霄，刘国政，孟宣市，等.飞翼布局纵向气动特性的等离子体激励控制[J]. 高电压技术，2018，44（9）：3049—3057.

LONG Y X，LIU G Z，MENG X S，et al. Longitudinal aerodynamic control over flying wing using plasma actuators [J]. High Voltage Engineering，2018，44（9）：3049—3057.（In Chinese）

[13]  吴云，李应红. 等离子体流动控制研究进展与展望[J]. 航空学报，2014，36（2）：381—405.

WU Y，LI Y H. Progress and outlook of plasma flow control [J]. Acta Aeronautica et Astronautica Sinica，2015，36（2）：381—405. （In Chinese）

[14]  SHYY W，JAYARAMAN B，ANDERSSON A. Modeling of glow discharge-induced fluid dynamics [J]. Journal of Applied Physics，2002，92（11）：6434—6443.

[15]  傅鑫. 一种基于低温等离子体的流动控制技术研究[D]. 南京：南京理工大学理学院，2007：15—19.

FU X. Investigation of flow control technology based on plasma[D]. Nanjing：School of Science，Nanjing University of Science and Technology，2007：15—19. （In Chinese）

[16]  CHOI H，LEE J，PARK H. Aerodynamics of heavy vehicles[J]. Annual Review of Fluid Mechanics，2014，46（1）：441—468.

[17]  刘畅. 重型载货汽车的空气动力特性研究[D]. 长春：吉林大学汽车工程学院，2008：30—37.

LIU C. Research on aerodynamic characteristics of heavy-duty truck [D]. Changchun：College of Automotive and Engineering，Jilin University，2008：30—37. （In Chinese）