两嵌段共聚物在扁长形受限空间的相行为研究

郭坤琨 吴凯 韩文驰

摘   要：应用自洽场方法模拟计算了本体结构为柱状相的AB两嵌段共聚物在球形和扁长形三维受限空间下的自组装行为. 通过改变受限空间的尺寸，系统总结了AB两嵌段共聚物在球形和扁长形受限下的相形态、自由能、构象熵和相互作用能的变化规律并做了比较研究. 结果表明，在受限体系中，嵌段共聚物会呈现出多样的相形态;在球形受限中，嵌段共聚物的相形态由于在不同方向上受限程度相同而表现出较好的结构对称性;而在扁长形受限中，共聚物分子链在不同维度方向上会受到不同程度的伸展取向限制，从而其相结构的对称性会被破坏.

关键词：自洽场理论;嵌段共聚物;扁长形;球形;受限尺寸;相结构

Abstract：In the present study， the phase behaviors of the bulk columnar phase AB diblock copolymers under spherical and prolate confinements are studied by the self-consistent field theory. By changing the size of the confined spaces， the developing law of phase morphology， free energy， conformational entropy and interaction energy of AB diblock copolymers are systematically summarized and compared. The results show that，in the confined spaces， diblock copolymers possess various phases. In the spherical confinement， the phase structures of diblock copolymers exhibit better symmetrical characteristics due to the identical frustration suffered from different dimensions. However， because the different frustrations and orientations of polymer chain in different dimension directions are introduced by prolate confinements， the phase structural symmetry of diblock copolymers was significantly broken.

Key words：self-consistent field theory;diblock copolymer;prolate;sphere; confined sizes;phase behavior

嵌段共聚物是由两种或两种以上不同性质的高分子链通过共价键连接形成的聚合物. 由于各嵌段间的物理和化学性质不同会发生微相分离形成不同的相结构，从而在传感器[1-2]、药物缓释材料[3-5]、光学材料[6]等诸多领域有着很大的应用前景. 为了更好地控制嵌段共聚物的相结构与性能，实验与理论上都对嵌段共聚物在受限空间内的丰富自组装行为进行了广泛研究. 受限空间能够打破嵌段共聚物本体相结构的对称性，并且受限空间的尺寸和内在物理性质对共聚物自组装行为也有着显著影响[7].

按受限空间的维度可以分为一维、二维及三维受限. 一维受限的研究主要集中在平行板受限方面，实验[8-10]和理论[11-13]的研究都表明嵌段共聚物的相结构会由于空间受挫而形成不同于本体的取向，从而呈现出多样的相形态. 如Yang等[14]采用自洽场理论模拟了本体为柱状相结构的AB两嵌段共聚物在平行板间的受限行为，由于嵌段共聚物与平行板间的相互作用，共聚物除了柱状相之外，還获得了穿孔层状、平直层状等更复杂的相形态;Li等[15]给出了相对完善的AB两嵌段共聚物在平行板受限时的自组装相图. 二维受限通常指圆柱形受限，在实验[16-18]与理论[19-22]上也已经有了较为广泛的研究. 结果表明受限壁的性质和尺寸大小都会对嵌段共聚物的自组装行为产生很大影响[23-24]. Yu等[25]用退火性蒙特卡罗方法分别模拟本体为层状相和柱状相AB两嵌段共聚物在圆柱形受限下的自组装行为，得到了螺旋结构、同心穿孔结构、堆叠环形等复杂结构. 如果进一步增加受限空间的维度，三维受限空间内几何结构将会变得更加复杂多样. 其中，球形受限是当前研究的一种典型的三维受限体系. 实验研究[26-31]观察到嵌段共聚物纳米颗粒会表现出独特的内部结构，如洋葱状同心层薄片结构、螺旋状结构或Janus型结构等丰富的相形态. 理论计算和模拟也预测了本体为层状相的嵌段共聚物也可表现出螺旋状结构、垂直结构和同心层薄片结构等[32-33];而本体相为柱状相的嵌段共聚物则表现出更加复杂的相结构，如单螺旋、双螺旋、堆叠环形等结构[25，34-35]. 椭球形受限[25]和软受限[36-37]等三维受限空间下共聚物相行为的研究近年也逐渐受到研究人员的关注. Yu等[25]通过退火性蒙特卡罗方法模拟发现本体为柱状相的AB两嵌段共聚物在椭球形受限空间中可表现出交叉柱状相、扁柱状相、单螺旋柱状以及细长球形等相结构. Yan等[37]应用实验和蒙特卡罗模拟方法研究了本体为柱状相的AB两嵌段共聚物在软受限情况下的相行为，得到了Janus状结构以及三角状结构等.

嵌段共聚物在三维受限中会严重受挫，它的定向结构不能像其本体一样得到很好的取向和松弛. 目前三维受限空间的研究主要集中于球形受限，而对于其他受限空间几何结构的研究较少，我们将在本文中初步考察在不同维度具有不同尺度的受限空间下嵌段共聚物的复杂相行为. 基于Helfrich形态方程[38]，可以计算出一系列具有轴对称的三维受限空间. 本文选取了不同约束空间但是具有相同约化体积的扁长形体作为三维受限空间，应用自洽场理论方法研究本体为柱状相时AB两嵌段共聚物的相行为.

1   理论与模型

考虑体积V中具有不可压缩性AB两嵌段共聚物的体系，设定A嵌段和B嵌段具有等效的链段长度b，聚合物总链长为N，A和B嵌段的链长分别为NA和NB，A嵌段的体积分数为fA = NA /N，而B嵌段的体积分数为1 - fA，两种不同嵌段单体之间的相互作用参数为χAB. 为了描述AB两嵌段共聚物在空间分布的尺寸大小，选取聚合物链的链段长度b作为单位长度. 基于理想高斯链模型的自洽场理论，体系的自由能可写为：

AB两嵌段共聚物的自由能是由聚合物不同组分之间的相互作用能U、构象熵-TS以及聚合物与受限壁之间的相互作用能H组成，即F=U-TS+H. 从而，AB两嵌段共聚物的各部分能量表达式分别为：

式中：H、K和c0分别为曲面的平均曲率、高斯曲率以及自发曲率;λ和ΔP分别为限制膜泡面积和体积的Langrange因子;κ为弯曲刚性模量. 通过求解普适形状方程可以得到球形和扁长形两种具有轴对称的二维封闭曲线. 通过旋转对称轴，我们可以得到不同形状的三维封闭曲面，从而可以得出受限界面的密度分布函数?W（r），其中，空间位置r位于三维封闭曲面内部时，?W（r） = 0，而r位于三维封闭曲面外部时?W（r）=1. 在不改变三维受限空间约化体积v的基础上，改变三维受限空间的体积以获得不同空间约束下柱状相AB两嵌段共聚物的自组装相行为，其中约化体积是指三维受限空间的体积V与该三维受限空间具有相同表面积A0的球形空间体积之比，v=6V/A3/20   ，球形的约化体积为1，本文选取的扁长形的约化体积均为0.81.

2   结果与讨论

对于扁长形三维受限和球形受限，本文只讨论受限壁性质为中性条件，即χAW = χBW = 0时，本体为柱状相AB两嵌段共聚物的自组装行为，见图1，选取聚合物的链长为N = 128，链段离散为ds = 1/128，空间大小为Lx × Ly × Lz = 32 × 32 × 64，离散大小为Nx × Ny × Nz = 32 × 32 × 64. 对于受限壁为中性的球形受限来说，随着嵌段共聚物各嵌段之间的相互作用参数χAB N的变化，嵌段共聚物的自组装行为也会发生变化，当柱状相AB两嵌段共聚物为弱相分离时，倾向于形成穿孔球层状结构和空心球层状结构;而柱状相AB两嵌段共聚物为强相分离时，则倾向于形成整体分散性液滴状结构或者是内层空心球层状结构[34-35].本文中A嵌段和B嵌段的相互作用参数为χAB N = 30（强分凝区）. FA = 0.25时本体相为六角排列的柱状相结构，其相周期L = 3.8Rg，这与Li等[35]计算结果一致. 假定链段长度b约为6 nm，聚合物链的回旋半径Rg和本体相周期L分别为27.7 nm和105.3 nm，这是在实验中非常容易获得的微纳尺度的受限空间.

图2给出了计算得到不同形状的体积V/R3g和所对应的假定为球体时直径D/Rg的关系.从图中可以看出它们完全满足球形的标准关系式V/R3g =π（D/Rg）3/6. 因此，本文中将以不同形状所对应球体的直径D/Rg定义为受限空间长度来描述柱状相AB两嵌段共聚物的受限程度.

为了比较球形和扁长形三维空间受限，图3给出了不同受限空间长度下球形和扁长形受限的相結构，图中只显示A嵌段，光滑的封闭曲线为受限空间的简化二维图. 从图3中可以看出，这些相结构和本体柱状相呈现出明显差别，而且随着受限空间尺寸变大，得到的相结构变得越复杂.

在球形受限中，当D/Rg ≤ 5.0时，即受限空间直径约为一个本体相周期（L = 3.8Rg）长度，计算得到的相结构为水滴状结构（类似Janus相结构），这和已有用自洽场理论模拟柱状相AB两嵌段共聚物在球形受限下得到的相结构相似[35]，而实验研究也表明嵌段共聚物PS-b-P4VP在软受限中的自组装行为也呈现出相似的相结构[41];当5.2 ≤ D/Rg ≤ 5.4时，计算结果得到4个液滴状的结构，这和以前采用自洽场理论模拟柱状相AB两嵌段共聚物在球形受限下的研究中得到的相结构相似[34]，实验中也观察到PS-b-P4VP共聚物在软受限中的自组装行为中会呈现出类似的相结构[42].这些相结构都属于单层相结构. 当受限空间直径进一步增大至5.6≤D/Rg≤6.6时，计算得到的相结构均为双层相结构. 其中，当5.6≤D/Rg≤6.0时，计算得到的相结构，表现为球中央为一个球状结构，而球外围呈现出两个液滴状结构;当6.2≤D/Rg≤6.6时，相结构表现为球中央具有一个球状结构，而球外围呈现出3个对称的液滴状结构. 这些双层结构与已有自洽场理论计算得到柱状相AB两嵌段共聚物在球形受限下的相结构非常相似[34-35].

在扁长形三维受限中，当2.2≤D/Rg≤2.8时，其相结构为液滴状结构，而当受限大小D/Rg增大至3.0时，计算得到的相结构为对称的双液滴状结构，这些结果都和球形受限中得到的相结构类似，其原因主要是由于受限空间尺寸较小，嵌段共聚物受到强烈受挫从而造成高分子链伸展被过度限制的缘故. 图4给出了AB两嵌段共聚物在D/Rg =3.0时扁长形受限下的自组装示意图. 随着受限空间增大至3.2≤D/Rg≤3.8，相结构表现为处于受限空间中央位置的弯曲层状结构，类似结构在蒙特卡罗模拟ABA三嵌段共聚物软受限时被观察到[42]. 当受限尺寸进一步增大至4.0≤D/Rg≤4.8时，相结构表现为处于受限空间中央的封闭层状环形结构，这与实验中AB两嵌段共聚物在椭球形受限中得到的相结构类似[37].当5.0≤D/Rg≤5.4时，相结构表现为扁长形受限中央呈现出一个环形结构，环形结构的两边各分布一个液滴状结构，这与已报道的柱状相AB两嵌段共聚物在软受限空间中得到的相结构相似[36].当受限尺寸D/Rg进一步增大至5.6≤D/Rg≤5.8时，相结构具体表现为受限中央形成一个弯曲的片状结构，而受限空间两极各有一个液滴状的结构;这种结构与采用蒙特卡罗模拟ABA三嵌段共聚物软受限时的结构具有一定相似性，最主要的差别是中央的弯曲片状结构变成了弯曲的柱状结构[41]. 当6.0≤D/Rg≤6.2时，计算得到的相结构和在5.6≤D/Rg≤5.8时得到的相结构类似，中间弯曲的片状结构转变成曲率半径和长度都变大的片状结构;这是由于随受限空间尺寸的增大，A嵌段可以得到较为良好的取向伸展的缘故. 随着受限空间的进一步增大至D/Rg = 6.4，体系相结构表现为一个中间弯曲的片状结构和分散在两极的3个液滴状结构，此时受限空间最大的曲率半径约为3.9Rg，接近于嵌段共聚物的本体相周期L. 当D/Rg高达6.6时，扁长形受限的相结构则出现了与球形受限相似的结构，具体表现为受限空间中央有一个球状结构以及球外围两极呈现出对称的3个液滴状结构.

本文中得到的球形受限下的相结构和受限程度的变化趋势与以前的研究结果基本一致[34].   对于球形受限和扁长形三维受限，当受限空间尺寸较小时，嵌段共聚物链均受到强受挫效应，相同体积的不同受限空间所得到的相结构具有一定相似性;而当受限空间尺寸增大到一定程度时，相同体积的不同受限空间得到的相结构完全不同，这表明受限空间形状会对嵌段共聚物的自组装行为产生较大影响[25].

图5为本体柱状相AB两嵌段共聚物在球形和扁长形三维受限空间中的自由能随受限空间尺寸D/Rg的变化. 从图中可以看出，不同受限空间下的AB两嵌段共聚物的自由能都随着受限空间的增大而减小，如果受限尺寸无限大，则高分子链无限接近其本体的相行为，高分子链的受挫程度不断减弱. 同时，图5结果还表明，受限空间尺度相同时，AB两嵌段共聚物在扁长形受限下的自由能均大于球形受限下的自由能. 因为扁长形的约化体积为v = 0.81，这说明当受限空间尺度相同时，扁长形受限空间的短轴尺寸小于受限空间尺寸D/Rg，即高分子链在扁长形受限空间中受挫程度更强烈，分子链会受到更严重的伸展取向限制.

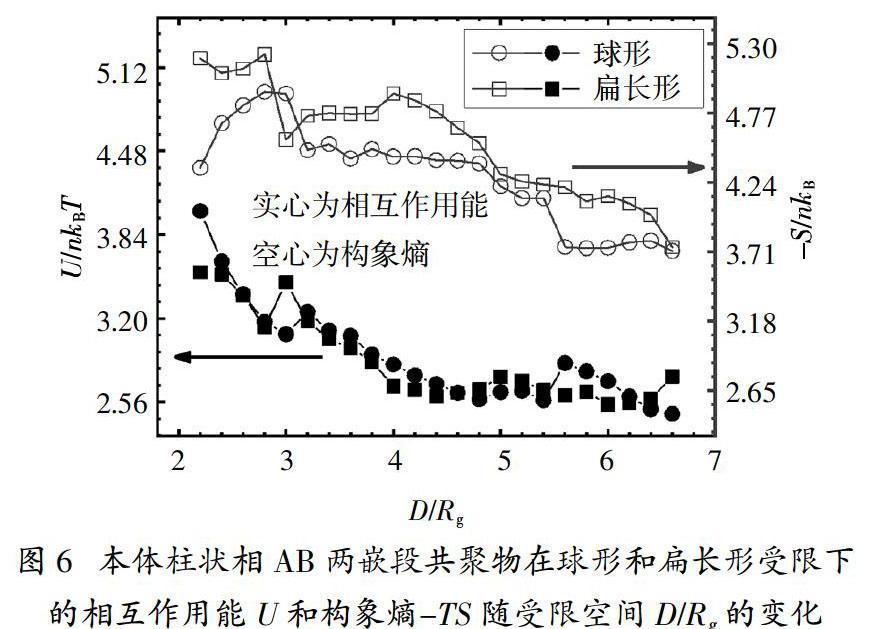
为了进一步理解在这两种三维受限空间中本体柱状相AB两嵌段共聚物相行为随受限空间尺寸变化的原因，我们分别从体系构象熵和相互作用能的变化角度做出解释. 图6给出了在这两种受限空间中本体柱状相AB两嵌段共聚物的相互作用能U和构象熵-TS随受限空间尺寸D/Rg的变化. 从图6中可以看出，本体柱状相AB两嵌段共聚物在球形受限中的构象熵大部分都小于扁长形受限的构象熵，这也进一步说明聚合物链在扁长形受限中的伸展取向限制更强烈，导致构象熵增大;而两种受限空间下柱状相AB两嵌段共聚物的相互作用能则差别较小，随着受限空间的变大，相互作用能的趋势都是逐渐减小. 当D/Rg分别为3.0、5.0、6.6时，扁长形受限下的柱状相AB两嵌段共聚物的构象熵和相互作用能都呈现出明显的波动，而相应的相形态也呈现出明显的变化，如从单个液滴状到两个对称液滴状相结构的转变等;在球形受限中，当D/Rg分别为3.2、5.0、5.6时，柱状相AB两嵌段共聚物的构象熵和相互作用能也表现出明显的波动，其相应的相形态也表现出明显的结构转变.

3   结   论

基于求解Helfrich形态方程可获得球形和扁长形两种具有轴对称的二维封闭曲线，通过旋转其对称轴，可得到三维轴对称球形受限空间和扁长形受限空间的密度分布函数. 本文采用自洽场理论模拟研究了本体为柱状相的AB两嵌段共聚物在受限壁为中性的球形受限以及扁长形受限下的自组装行为. 研究结果表明，三维空间受限下AB嵌段共聚物的相行为明显不同于本体柱状相. 改变球形受限以及扁长形受限空间尺度的大小，可得到本体为柱状相AB两嵌段共聚物的相形态和能量随受限程度的变化规律. 计算结果显示柱状相AB两嵌段共聚物在扁长形受限下会表現出更强烈的受挫和取向限制. 从相形态的演变中，我们发现在扁长形受限下，由于共聚物分子链在不同维度方向上会受到不同程度的伸展取向限制，共聚物相形态的对称性被明显破坏;而在球形受限中，嵌段共聚物的相形态由于在不同方向上受限程度相同而表现出较好的结构对称性. 此外，在扁长形受限和球形受限下，本体柱状相AB两嵌段共聚物的自由能随着受限空间的增大均变小，但是嵌段共聚物在扁长形受限下的自由能要大于球形受限下的自由能. 本研究不仅可以提高人们对嵌段共聚物在三维空间受限下相行为的认知，还有助于指导实验中的设计方案以获得具有更丰富内部结构的不同形态微纳粒子.

参考文献

[1]    LARSSON E M，ALEGRET J，MIKAEL K，et al. Sensing characteristics of nir localized surface plasmon resonances in gold nanorings for application as ultrasensitive biosensors[J].  Nano Letters，2007，7（5）：1256—1263.

[2]    WANG Y，DENG J J，DI J W，et al. Electrodeposition of large size gold nanoparticles on indium tin oxide glass and application as refractive index sensor[J]. Electrochemistry Communications，2009，11（5）：1034—1037.

[3]    SILVA A K A，RICHARD C，BESSODES M，et al. Growth factor delivery approaches in hydrogels[J]. Biomacromolecules，2009，10（1）：9—18.

[4]    JUNG J，LEE I H，LEE E，et al. pH-sensitive polymer nanospheres for use as a potential drug delivery vehicle[J]. Biomacromolecules，2007，8（11）：3401—3407.

[5]    ZHANG C Y，YANG Y Q，HUANG T X，et al. Self-assembled pH-responsive MPEG-b-（PLA-co-PAE） block copolymer micelles for anticancer drug delivery[J]. Biomaterials，2012，33（26）：6273—6283.

[6]    HUTTER E，FENDLER J H. Exploitation of localized surface plasmon resonance[J]. Advanced Materials，2004，16（19）：1685—1706.

[7]    JIN Z，FAN H. Self-assembly of nanostructured block copolymer nanoparticles[J]. Soft Matter，2014，46（10）：9212—9219.

[8]    HARRISON C，PARK M，CHAIKIN P，et al. Depth profiling block copolymer microdomains[J]. Macromolecules，1998，31（7）：2185—2189.

[9]    BUSCH P，POSSELT D，SMILGIES D M，et al. Lamellar diblock copolymer thin films investigated by tapping mode atomic force microscopy：molar-mass dependence of surface ordering[J]. Macromolecules，2003，36（23）：8717—8727.

[10]  TSARKOVA L，KNOLL A，KRAUSCH G，et al. Substrate-induced phase transitions in thin films of cylinder-forming diblock copolymer melts[J]. Macromolecules，2006，39（10）：3608—3615.

[11]  MENG D，WANG Q. Complex morphologies in thin films of symmetric diblock copolymers as stable and unstable phases [J]. Soft Matter，2010，6（23）：5891—5906.

[12]  MISHRA V，FREDRICKSON G H，KRAMER E J. SCFT simulations of an order-order transition in thin films of diblock and triblock copolymers [J]. Macromolecules，2011，44（13）：5473—5480.

[13]  KIM H，KANG B G，CHOI J，et al. Morphological behavior of A2B block copolymers in thin films[J]. Macromolecules，2012，51（3）：1181—1188.

[14]  YANG Y，QIU F，ZHANG H，et al. Cylindrical phase of diblock copolymers confined in thin films. A real-space self-consistent field theory study[J]. Polymer，2006，47（6）：2205—2216.

[15]  LI W H，LIU M J，QIU F. Phase diagram of diblock copolymers confined in thin films[J]. Journal of Physical Chemistry B，2013，117（17）：5280—5288.

[16]  XIANG H，SHIN K，KIM T，et al. Block copolymers under cylindrical confinement[J]. Macromolecules，2004，37（15）：5660—5664.

[17]  DOBRIYAL P，XIANG H，KAZUYUKI M，et al. Cylindrically confined diblock copolymers[J]. Macromolecules，2009，42（22）：9082—9088.

[18]  MA M，TITIEVSKY K，THOMAS E L，et al. Continuous lamellar block copolymer nanofibers with long range order[J]. Nano Letters，2009，9（4）：1678—1683.

[19]  LI W H，WICKHAM R A，GARBARY R A. Phase diagram for a diblock copolymer melt under cylindrical confinement[J]. Macromolecules，2006，39（2）：806—811.

[20]  LI W H，WICKHAM R A. Influence of the surface field on the self-assembly of a diblock copolymer melt confined in a cylindrical nanopore[J]. Macromolecules，2009，42（19）：7530—7536.

[21]  LAACHI N，DELANEY K T，KIM B，et al. Self-consistent field theory investigation of directed self-assembly in cylindrical confinement[J]. Journal of Polymer Science Part B：Polymer Physics，2015，53（2）：142—153.

[22]  WANG Y，HAN Y，CUI J，et al. Monte carlo study of degenerate behavior of AB diblockcopolymer/nanoparticle under cylindrical confinement[J]. Langmuir，2016，32（33）：8484—8493.

[23]  CHEN P，HE X，LIANG H. Effect of surface field on the morphology of a symmetric diblock copolymer under cylindrical confinement[J]. The Journal of Chemical Physics，2006，124（10）：104906.

[24]  LI S，WANG X，ZHANG L，et al. Concentric lamella structures of symmetric diblock copolymers confined in cylindrical nanopores[J]. Polymer，2009，50（21）：5149—5157.

[25]  YU B，LI B，JIN Q，et al. Confined self-assembly of cylinder-forming diblock copolymers：effects of confining geometries[J]. Soft Matter，2011，7（21）：10227—10240.

[26]  ARSENAULT A C，RIDER D A，TETREAULT N，et al. Block copolymers under periodic，strong three-dimensional confinement[J]. Journal of the American Chemical Society，2005，127（28）：9954—9955.

[27]  HIGUCHI T，MOTOYOSHI K，SUGIMORI H，et al. Three-dimensional observation of confined phase-separated structures in block copolymer nanoparticles[J]. Soft Matter，2012，8（14）：3791—3797.

[28]  HIGUCHI T，AJIMA A，MOTOYOSHI K，et al. Frustrated phases of block copolymers in nanoparticles[J]. Angewandte Chemie International Edition，2010，47（42）：8044—8046.

[29]  AVALOS E，HIGUCHI T，TERAMOTO T，et al. Frustrated phases under three-dimensional confinement simulated by a set of coupled Cahn-Hilliard equations[J]. Soft Matter，2016，12（27）：5905—5914.

[30]  HIGUCHI T，PINNA M，ZVELINDOVSKY A V，et al. Multipod structures of lamellae-forming diblock copolymers in three-dimensional confinement spaces：experimental observation and computer simulation[J]. Journal of Polymer Science Part B：Polymer Physics，2016，54（17）：1—8.

[31]  RAHIKKALA A，SOININEN A J，RUOKOLAINEN J，et al. Self-assembly of PS-b-P4VP block copolymers of varying architectures in aerosol nanospheres[J]. Soft Matter，2013，9（5）：1492—1499.

[32]  YU B，LI B，JIN Q，et al. Self-assembly of symmetric diblock copolymers confined in spherical nanopores [J]. Macromolecules，2007，40：9133—9142.

[33]  SHI A C，LI B. Self-assembly of diblock copolymers under confinement[J]. Soft Matter，2013，9：1398—1413.