基于稳健估计的硫酸钙光谱值抗差能力分析
2020-07-03刘暑明董元杨华文
刘暑明,董元,杨华文
(华北理工大学 矿业工程学院,河北 唐山 063210)
0 引言
光谱数据的拟合分析可以反映光谱反射率与化合物质量之间的线性关系,拟合得准确与否会影响化合物的定性与定量的数据分析结果,在光谱数据的采集过程中,由于测量时间较长、加之外部环境的干扰等,会导致测量出来的光谱数据存在粗差。在不含粗差的情况下,一般使用最小二乘法回归分析进行处理,拟合的效果较好;在含有粗差的情况下,一般使用稳健估计法来削弱粗差对结果的影响,获得最接近真实值的最佳估值。国内学者在应用稳健估计处理光谱数据方面研究较少,董元等采用稳健估计和最小二乘回归分析的方法,分别对水泥的胶砂试块光谱值进行抗差能力分析,结果表明,在含有噪声时,稳健估计的抗差效果较好[1],除此之外,稳健估计在其它领域有广泛应用。曹兰杰等在GNSS高程拟合的粗差探测中应用了稳健估计,通过与最小二乘法求解的精度进行比较,结果表明,稳健估计在抗差方面有更大的能力[2]。赵晓囡等以3个具有不同观测值数量和未知数数量的水准网为例,通过仿真实验比较了13种常用稳健估计方法的稳健性。结果表明,无论是具有独立等权观测值的水准网还是具有独立不等权观测值的水准网,L1法、Danish法、German-McClure法和IGGIII方案比其他常用稳健估计方法能更有效地消除或减弱粗差的影响[3]。从以上的研究中可以发现,稳健估计法有很好的抗差效果,应用于硫酸钙模型的建立效果更好。
硫酸钙的光谱值存在粗差,为了研究硫酸钙浓度和反射率的线性关系,提取3 g、6 g、9 g硫酸钙在572.5 nm、1 487.9 nm、1 935 nm、2 100.6 m、2 337.7 nm 5个波段处去除包络线的反射率,分别采用最小二乘回归分析和稳健估计进行比较分析,构建相应的线性回归模型,以此对比存在粗差和剔除粗差时2种方法的拟合效果。
1 2种方法的应用原理
硫酸钙特征曲线图像如图1所示,由图1可以看出,硫酸钙有6个明显的吸收位置,分别为387.4 nm,572.5 nm,1 487.9 nm,1 935 nm,2 100.6 nm,2 337.7 nm。通过对6个吸收位置的相关性分析,能够得出最能代表与硫酸钙浓度变化相关的吸收位置。
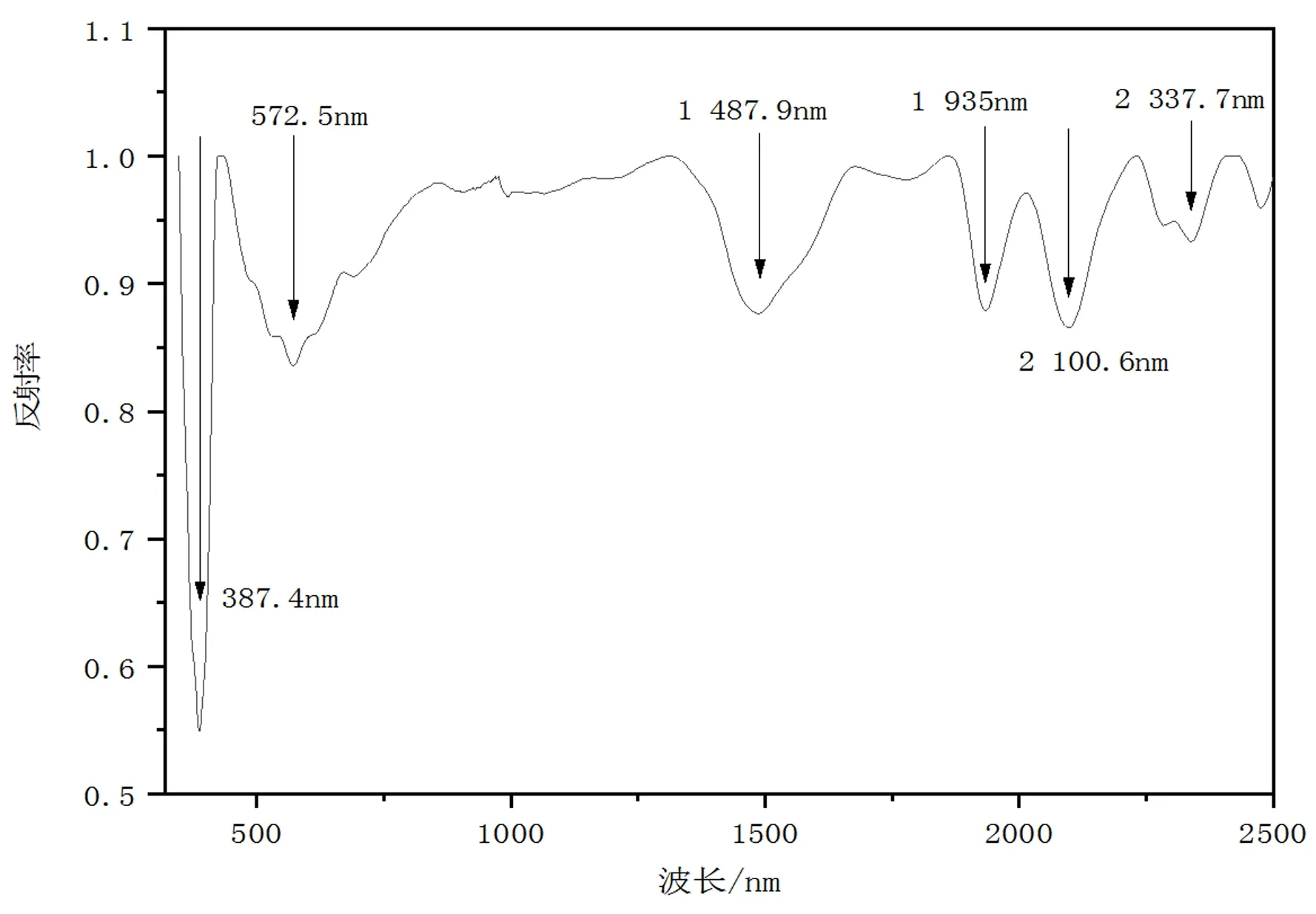
图1 硫酸钙特征曲线
光谱数据是在6个吸收位置上硫酸钙的光谱值及与之对应的浓度值,结合吸收位置建立模型,该模型所用到回归方程如下:
Y=β0+β1X1+β2X2+β3X3+β4X4+β5X5+β6X6
(1)
其中X1、X2、X3、X4、X5、X6为不同吸收位置对应的光谱值,β0、β1、β2、β3、β4、β5、β6为回归系数,Y为浓度。
一般情况下使用最小二乘法进行回归分析,对数据进行拟合,并且拟合结果较为精准,但当测量的光谱数据存在噪声时,拟合结果不再准确,因此一般采用稳健估计法进行拟合,拟合效果更精准。本研究拟采用2种方法分别获得结果,通过中误差和残差平方和来对比两者的不同。
1.1 原理对比
表1所示为最小二乘法和稳健估计法原理。

表1 原理对比
最小二乘法是假设观测值中只含有偶然误差,不含粗差,正因如此,从以上最小二乘法和稳健估计法的原理对比中可以看出,两者的最大区别在于权的选取,最小二乘法中每个自变量的权是相等的,即等权;稳健估计也叫抗差估计,正是针对最小二乘法的缺陷提出的,稳健估计对“权重”进行了改进,对于粗差,稳健估计分配较小的权,且逐次缩小权,最终使粗差的权重达到最低,减弱对结果的影响。稳健估计不追求绝对意义上的最优,而是在抗粗差前提下的最优或接近最优。
1.2 实验流程图
2种方法流程图如图2所示:
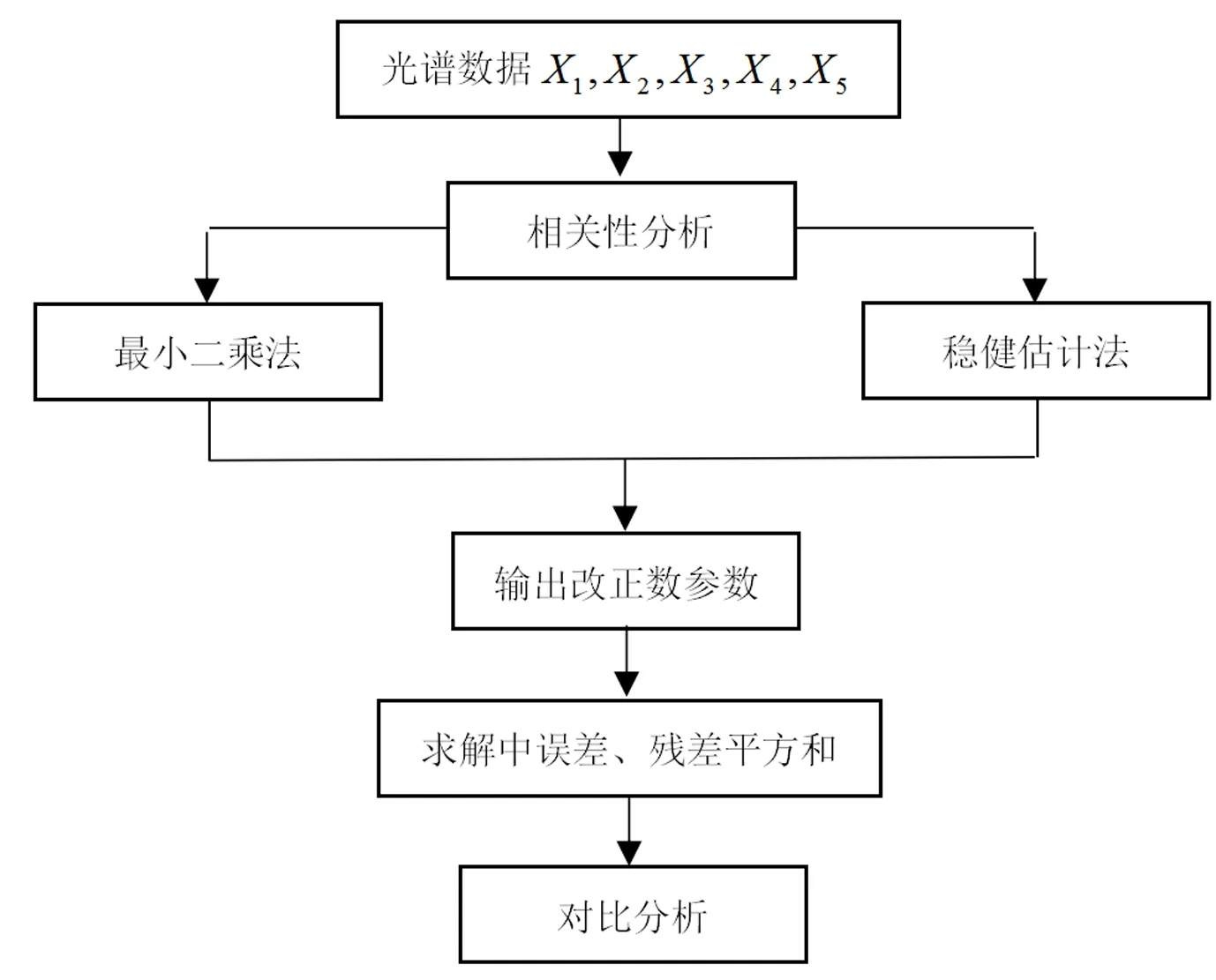
图2 流程图
本研究采用了最小二乘法和稳健估计法分别对光谱数据进行处理,对比2种方法求解的中误差、残差平方和,得出稳健估计在抗差方面的优点。
2 实验方案
2.1 原料
该项研究使用的光谱仪为SR2500,实验原料来源于天津市福晨化学试剂厂生产的分析纯硫酸钙。实验时,操作人员处于暗室以减弱其他光源的影响;测量枪应与被测物体所在水平面的法线的夹角保持在±10°左右,将硫酸钙粉末放置于黑色的小盒子中,将粉末均匀铺平于盒子底部。分析纯硫酸钙的主要性状如表2所示。

表2 分析纯硫酸钙的主要性状
2.2 光谱分析
经过测量,采集到不同波长下的光谱值,使用ENVI进行包络线去除,得到不同浓度光谱反射率图像,如图3所示。
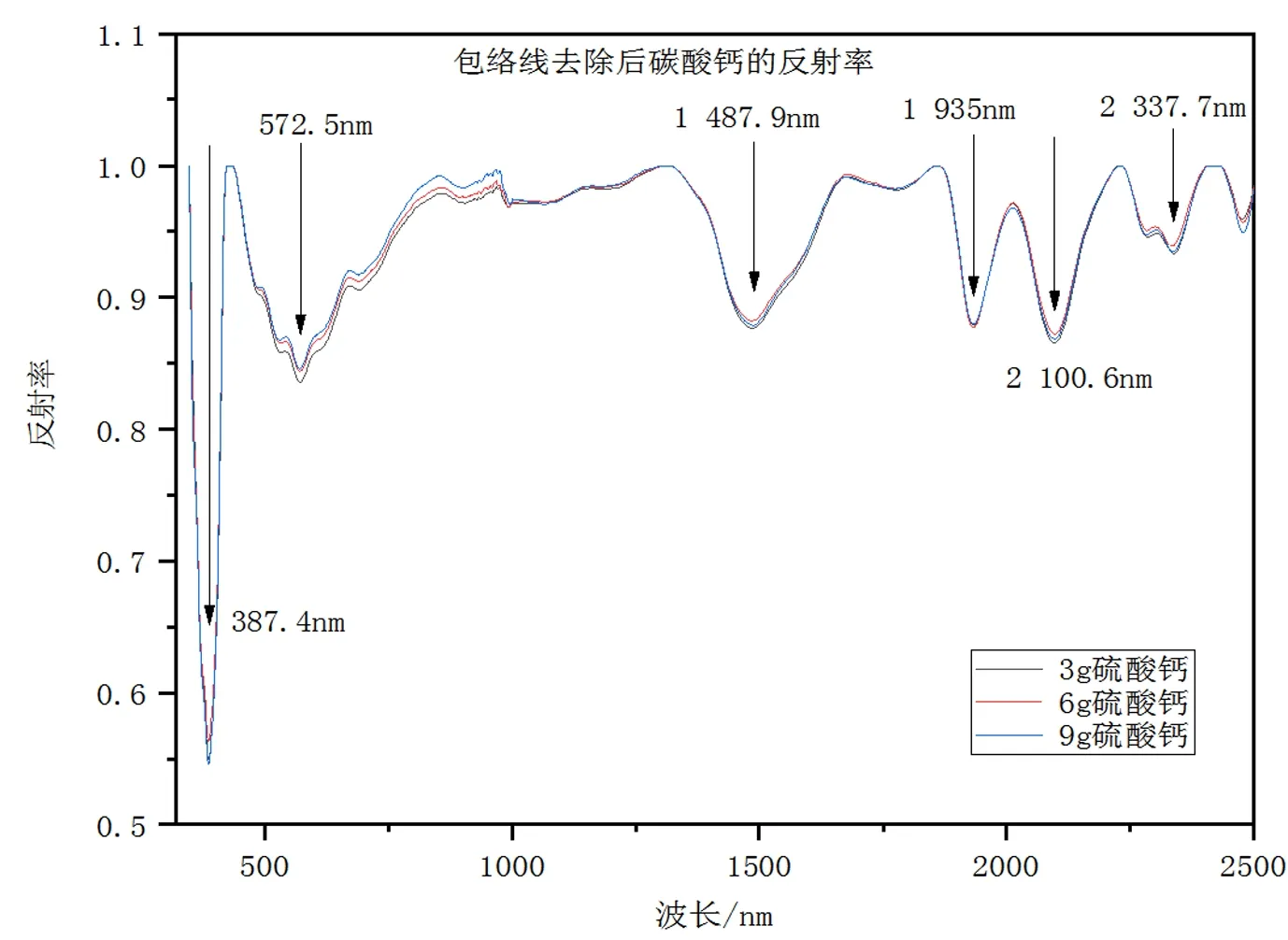
图3 3 g、6 g、9 g硫酸钙包络线去除后的光谱反射率图像
从以上的图像可以看出,3 g、6 g、9 g浓度的硫酸钙分别有6个明显的吸收位置,这是硫酸钙曲线的特征。在保证数据结果更为精确以及保证数据量足够大的情况下,同时也为了方便后期的数据分析,故选取5个波谷位置的反射率数据。本研究选取的5个吸收位置分别为:572.5 nm、1 487.9 nm、1 935 nm、2 100.6 nm、2 337.7 nm。
3 结果分析
处理后的数据存在明显的数据量较小,无法得出显著结果的问题,因此将处理后的光谱数据进行次样条插值,扩充数据量,插值后的数据如表2所示。对插值后的结果进行相关性分析,选取与硫酸钙浓度Y相关性最大的自变量X,分别进行最小二乘回归分析和稳健估计分析,以此来对结果进行对比分析。
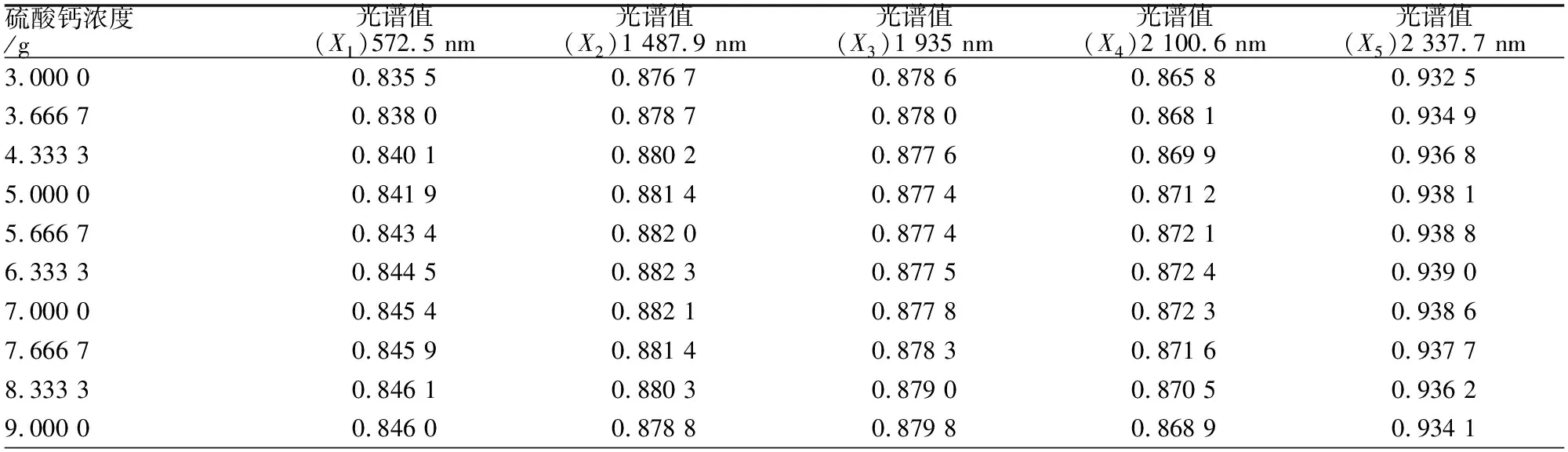
表2 原始数据
3.1 相关性分析

表3 相关性分析结果
在相关性分析的结果中,相关系数r的绝对值越接近1表示两者的相关性越高,p的值越小表示变量间相关性的显著性越高。从硫酸钙浓度和光谱反射率的相关性分析中可以得出,自变量X1的相关系数为r1=0.94,显著性p1=,因此在波长572.5 nm处的反射率X1和硫酸钙的浓度Y相关性最高,故选取X1与Y进行分析。
从原始数据可以看出,数据相差不大,为了使稳健估计的效果更加突出,故人为在变量X1中第6个至第8个数据里加入7倍中误差,使之成为较大的粗差,加入粗差后数据的结果为X1=[0.835 5, 0.838 0, 0.840 1, 0.841 9, 0.843 4, 0.845 4, 0.846 3, 0.846 8, 0.846 1, 0.846 0]。
3.2 数据分析
图4所示为原始数据残差图。
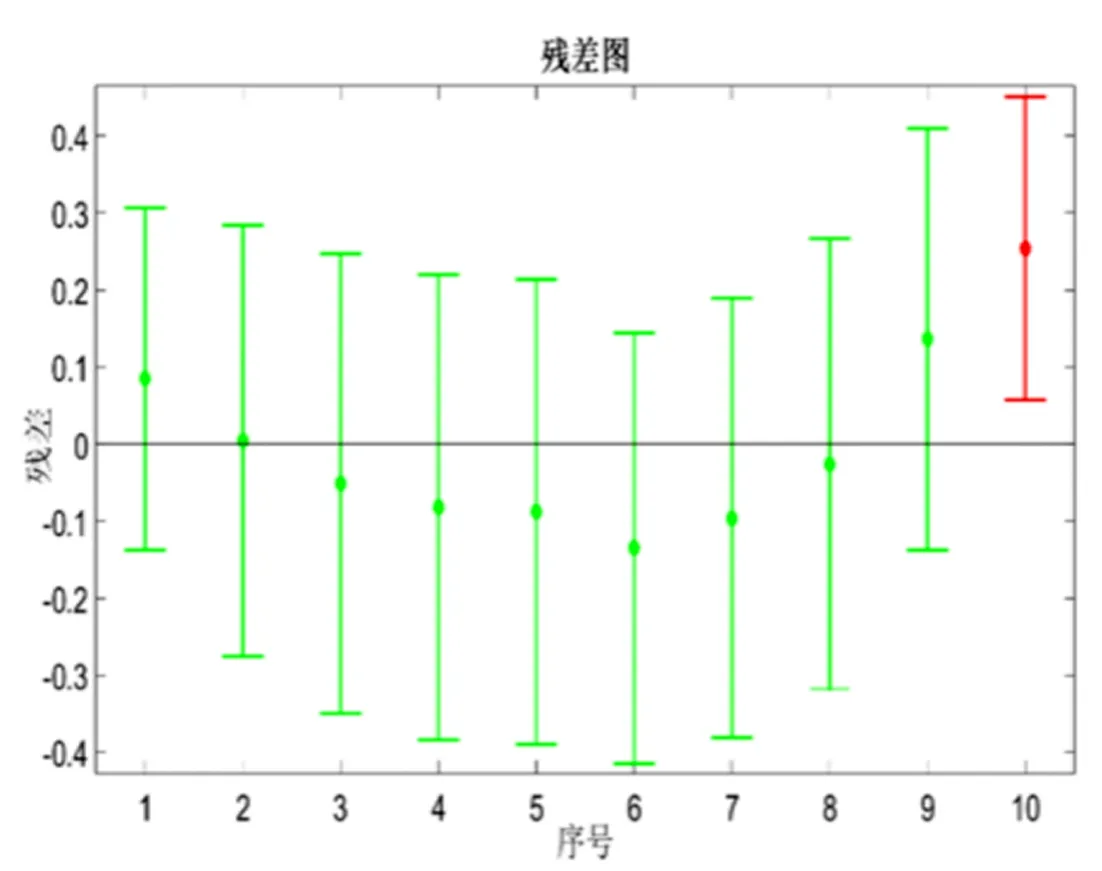
图4 原始数据残差图
从图4原始数据残差图可以看出,原始数据中的第10组数据出现明显的粗差,需要将其剔除。最小二乘法回归分析得到的系数为a1=0.889 08,b1=-0.097 43,所以得到的一元线性回归方程为:
Y1=0.890 13X-0.083 356
(2)
同理可得到稳健估计方程的系数a2=0.872 96,b2=-0.092 622,所以得到的一元线性方程为:
Y2=0.839 63X-0.070 348
(3)
式子中的Y1、Y2仅是为了区分不同的方程结果。表4表示存在残差时中误差和残差平方和的对比。

表4 存在残差时中误差和残差平方和
从表4的结果可以看出,2个方程的差异明显,在存在粗差时2种方法的中误差分别为s1=0.016 924,s2=0.011 167。通过中误差的对比可明显看出,利用稳健估计求得的中误差远小于利用最小二乘法,表明稳健估计法效果更好;另外,从残差平方和也能明显看出,稳健估计法的残差平方和小于最小二乘法得到的残差平方和;因此,结合中误差和残差平方和的对比可知,稳健估计的效果更佳。
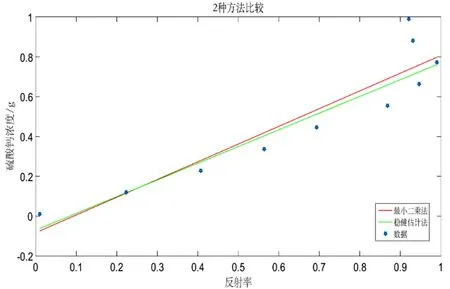
图5 数据结果图
从图5所示的2种方法的方程拟合图可以看出,原始数据散点分布较为均匀,第9个和第10个点的值偏离方程直线较远,认定为粗差,对拟合的直线有一定影响。从图5可以看出,最小二乘法的拟合直线受粗差的影响较大,并且直线向粗差方向偏移,而稳健估计法拟合的直线相对来说,受粗差影响较小,更加接近真实值。
4 结论
(1)在含有光谱数据噪声的情况下,稳健估计法计算的中误差和残差平方和小于最小二乘法,并且拟合的直线相对稳定,更接近真实值。
(2)稳健估计法能有效削弱粗差对光谱数据的影响,起到抗差的作用,并以此可以反演出硫酸钙的浓度。
