不同倒角形式对空腹梁受力性能影响的试验研究

徐宏广,冯庆兴,端木雪峰,徐铮弢,林皇诚

(1.浙江科技学院 土木与建筑工程学院,杭州 310023;2.中国联合工程有限公司,杭州 310052)

在满足强度要求的前提下,提高梁的截面高度可有效减小梁在荷载作用下的挠度。为节省材料、减轻结构自重、方便梁底管线布置并合理利用空间,可采用空腹梁替代实腹梁,空腹梁与楼板组合成组合空腹板。组合空腹板的下层通常采用型钢或焊接型钢形成双向肋,上层则采用钢筋混凝土双向带肋板或钢肋-混凝土薄板[1]。组合空腹板按上层体系的不同划分为第一类和第二类,与之对应的空腹梁也划分为第一类和第二类。杨期柱等[2]对第一类组合空腹梁在静力作用下的受力性能进行了研究，给出了上下肋的弯矩和轴力分布规律。黄勇等[3]在第一类组合空腹板基础上提出了将组合板上层的双向带肋板直接用较厚的钢筋混凝土平板代替,并进行了足尺模型试验和有限元分析，研究表明，对简支组合空腹梁，其下层钢肋处于拉-弯、上层混凝土板处于压-弯的受力状态。刘卓群等[4-6]对第二类组合空腹梁空腹段上下肋的内力计算进行了数值模拟和理论推导，分析表明，基于修正的空腹桁架理论计算方法能较为准确地计算出钢空腹梁关键截面的应力分布状况，计算方法可用于工程实践。陈强等[7-10]对组合空腹梁中受力比较复杂的部位——抗剪键节点处的受力性能进行了有限元分析，指出节点区域内各构件的接触面附近存在较大的应力集中现象，同时认为节点刚域对空腹梁整体的挠度影响较大，在简化计算时应考虑节点刚域的影响。随着组合空腹板在工程中运用日渐增多与技术的成熟,张华刚等[11-14]以组合空腹板楼盖整体为研究对象进行了试验并做数值分析，结果表明，此类结构具有刚度大、用钢量少等特点，有推广应用价值。姜岚等[15]通过对影响空腹梁挠度的跨高比、空腹率、网格尺寸等因素进行有限元分析,给出了T型钢空腹梁挠度的实用计算方法。

空腹梁作为组合空腹板的重要组成单元,有时也作为单独构件使用,其承载力、挠度、破坏形态等受诸多因素的影响,而目前单独对它进行研究的尚不多见，因此有必要通过专门的试验对这些影响因素进行分析研究。在前人研究成果的基础上,本文以上下肋均为T形的空腹梁为研究对象,通过设置倒角与否、倒角形式、孔洞长高比、开孔大小、孔洞分布等影响因素,研究空腹梁在静荷载作用下的承载力、挠度、等效刚度与各影响因素之间的关系。

1 试验设计

1.1 试件制作

空腹梁在倒角(无倒角时为抗剪键)与梁肋交接处受力较为复杂,容易出现应力集中现象,针对这一现象,我们设计了5根试验梁。梁B1为实腹梁,梁B2～B5均为有开孔的空腹梁。5根梁全长均为3 000 mm,梁横截面尺寸均为300、75、5、7 mm(高、宽、腹板厚度、翼缘厚度)。在抗剪键与上下肋交接处，梁B2和B3设置长50 mm、厚5 mm的等腰直角三角形倒角,梁B4设置半径50 mm、厚5 mm的1/4圆弧倒角,梁B5不设置倒角。试件制作时,将HN150×75×5×7型钢(试验前经实测,腹板厚4.8 mm、翼缘板厚6 mm)沿梁长在腹板处对称剖分成2个75×75×5×7 T形截面钢,分别作为梁的上下肋。实腹梁B1腹板处采用-5×150×3 000钢板加高,空腹梁端部抗剪键采用-5×150×200钢板,中部采用-5×150×100钢板，用E43型焊条将各组件焊接组合成空腹梁。试验梁所有部位材料均采用Q235钢。图1为试件加工图,图2为试件尺寸。

图1 试件加工图(单位:mm)Fig.1 Processing diagram of test specimen (unit: mm)

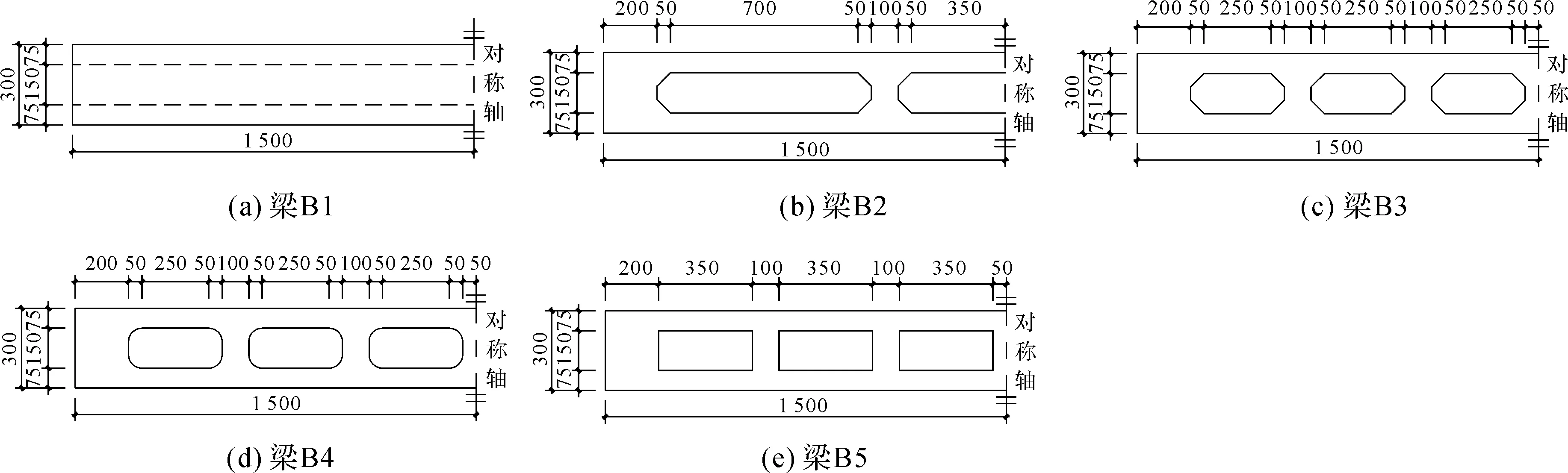
图2 试件尺寸(单位：mm)Fig.2 Size of test specimen (unit: mm)

1.2 试验方案

试验使用的主要仪器有:应变片,BX120-5AA(5×3)型电阻应变片;数据采集装置,DH3816N型静态应变测试系统;加载装置,MAS-500/2Q型电液伺服垂向加载作动器;位移计,成量川牌百分表,分度值0.01 mm,测量范围0～10 mm;自制抗倾覆装置,在距左右支座中心800 mm处对称设置抗倾覆装置,装置中间竖向槽宽85 mm,梁宽75 mm,梁翼缘板与竖向槽壁左右两侧各留有5 mm的间隙,并在竖向槽壁上涂抹机械润滑油脂,确保试验梁在加载过程中能在竖向平面内自由变形,且不至于过早出现平面外倾覆。

梁B2、B3的应变片布置如图3所示,梁B4、B5应变片分布与梁B3完全相同,梁B1应变片分布与梁B3基本上相同。

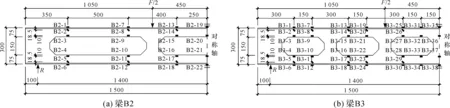
图3 梁B2、B3的应变片布置(单位：mm)Fig.3 Arrangement plan of beam B2, B3 strain gauge(unit: mm)

梁B5的加载位置及位移计布置如图4所示,以测量梁在各分级荷载作用下的挠度值。其余4根梁加载位置、位移计布置点均与梁B5相同。

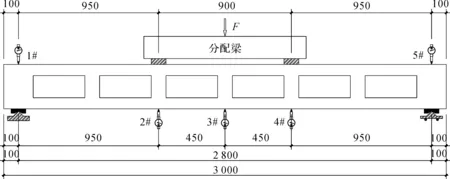
图4 梁B5加载位置及位移计布置(单位：mm)Fig.4 Arrangement of beam B5 loading position and displacement meter(unit: mm)

1.3 试验过程

图5 空腹梁的静力试验Fig.5 Static test of hollow beams

按简支梁工况进行试验,梁的左右支座中心距梁端均为100 mm,梁的计算长度l可取2 800 mm。通过分配梁对试件进行加载。按前述试验方案将试件安置在加载平台上,在预设测点处安装位移计,记录试件在其自重作用下各测点处的位移计初始值,放置分配梁后按单调静力加载方式进行加载,图5为试验过程。对梁进行分级加载,每级加载值为5 kN(指施加在分配梁上的总荷载值),加载速率2 kN/min。每级加载结束后,记录各测点处位移计读数。每级加载结束后持荷2 min,再进行下一级加载。试验过程中随时观察梁的变化,以梁加载至产生较大局部变形或整体失稳破坏作为终止加载条件。

2 试验结果及分析

2.1 空腹梁受力形态分析

由图2可知,梁B2与梁B3、B4、B5相比,除倒角设置和抗剪键数量不同外,主要区别在于孔洞尺寸不同。梁B2孔洞尺寸较大,使得孔洞四角处的倒角与上下梁肋交接处的破坏形态更加明显,图6为梁B2破坏后的变形形态。如图6(a)所示,梁B2在荷载作用下,破坏最早出现在等边直角三角形倒角与梁肋交接处,1#、4#点处呈现受拉破坏,2#、3#点处呈现局部受压破坏。按照GB 50017—2017 《钢结构设计标准》[16],取Q235钢屈服强度fy=235 N/mm2,弹性模量E=2.06×105N/mm2。弹性状态极限应变

(1)

图6 梁B2破坏后变形形态Fig.6 Deformation pattern of destroyed beam B2

据图3梁B2应变片布置并查梁B2应变片实测数据后发现:当加载至28 kN时,应变片B2-3(2#点)实测值最先到达-1 140×10-6,应变值为负,说明2#点受压破坏;加载至30 kN时,应变片B2-9(1#点)实测值达到+1 140×10-6,应变值为正,说明1#点受拉破坏;加载至36 kN时,应变片B2-10(3#点)实测值达到-1 140×10-6,说明3#点受压破坏;应变片B2-4(4#点)实测值虽没有达到+1 140×10-6,但应变值为正,说明4#点受拉。可见,应变片实测值与试验观察的梁变形形态相符。梁B2右端孔洞的变形如图6(f)所示,由矩形变为四边形,两组对角分别受拉与受压。空腹段在同一横截面处,上下梁肋受力性能呈现出独立性,与实腹梁在同一横截面上表现出的平截面假定不同。按图4加载时,实腹梁B1在支座附近处的弯矩值较小,使得此处应变值也较小,实测值也显示,梁B1最大应变发生在跨中的最下缘处。空腹梁B2支座附近,尽管此处梁整体弯矩值较小,但2#、4#点处应变值却较其他位置处大,梁上肋(下肋)在梁肋端部受力较大,在空腹段中间部位受力较小,空腹段梁肋受力显示不均匀性,这说明空腹梁的受力形态有别于实腹梁。倒角(无倒角时为抗剪键)与梁肋交接处是薄弱部位,受力复杂,应重点关注。

为验证试验结论的合理性,对试验梁采用Abaqus建模模拟分析。Abaqus建模时,取梁实测截面厚度,5根梁的网格划分近似全局尺寸取5 mm。梁体倒角采用楔形单元形状,单元体属性为C3D6,六结点线性三棱柱单元。梁体其他部位均采用六面体单元形状,单元体属性为C3D8R,八结点线性六面体单元,减缩积分。各梁试验变形和Abaqus模拟变形形态如图7所示。由图7所示的Abaqus模拟分析可知,梁B2在孔洞四角处的倒角与上下梁肋交接处应力值最先达到强度极限,与试验结果一致。其余3根空腹梁受力形态分析与梁B2相同。梁B2呈现出局部屈曲破坏,在空腹段,T形截面上肋(下肋)腹板由于开孔而处于无支状态(或悬挑状态)且腹板较薄,其无支长度与腹板厚度的比值较大,故在压力作用下容易发生局部屈曲破坏。梁B1呈现出整体失稳破坏,梁B3、B4、B5也出现了局部屈曲破坏,但破坏形态较梁B2弱,主要呈现出整体失稳破坏。由于梁B3、B4、B5的孔洞长高比减小,T形截面上肋(下肋)腹板沿梁长方向的无支长度减小,且梁肋在空腹段的受力较梁B2要均匀,故局部屈曲破坏形态减弱,但与梁B1相类似,试验梁受压上翼缘无平面外支撑而处于自由状态,使得梁横截面绕弱轴的长细比值较大,梁的稳定系数降低,故容易发生整体失稳。

图7 梁试验变形与模拟变形形态对比Fig.7 Comparision of beam deformation form between test and simulation

2.2 设置不同形式倒角时梁的受力性能

由2.1节分析可知,倒角与上下肋交接处是薄弱部位,最先出现局部屈曲破坏。为研究设置倒角与否及不同形式倒角对薄弱部位受力性能的影响,在其他条件均相同时,以梁B3、B4、B5为研究对象,利用试验实测值和Abaqus模拟值从承载力、挠度等角度对比分析梁的力学性能。

2.2.1 承载力

取试件产生较大局部变形或整体失稳破坏时的加载值作为试验最大加载值Fmax。以应变实测值达到±1 140×10-6作为梁达到弹性极限状态的限值,与之对应的加载值为Fe。在Abaqus模型中,找出与应变片实际粘贴位置相同的结点,对结点处的应力、应变值与实测值采取相同的方法进行分析。试件最大加载值Fmax、弹性加载值Fe见表1。

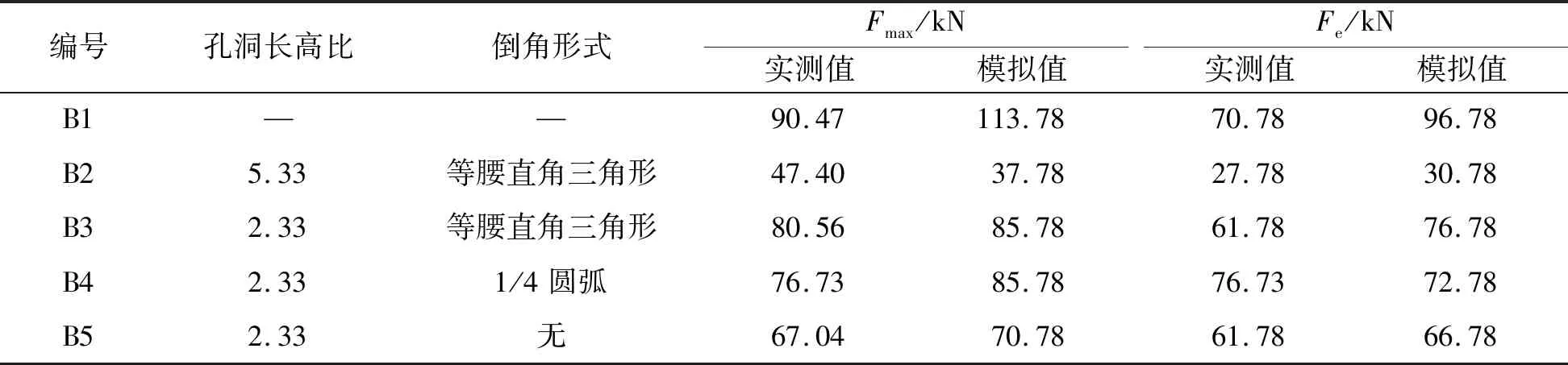
表1 梁最大加载值和弹性极限状态加载值Table 1 Maximum loading values and elastic limit state loading values of beams

梁B1的最大应变值出现在梁跨中,符合事实。梁B4的局部屈曲正好发生在倒角与梁肋交接点处,梁肋在空腹段中间部位的应力值较小,处于非均匀受力状态,即两端大中间小。试验时应变片的粘贴位置距离倒角与梁肋交接点50 mm,应变片长度5 mm,50 mm的距离正好使应变片避开了应力集中区域,故梁B4实际的Fe应小于76.73 kN。梁B5没有设置倒角,应变片粘贴位置距离抗剪键与梁肋交接点100 mm,避开了应力集中区域,故梁B5实际的Fe应小于61.78 kN。可同理分析梁B2、B3。

由表1可知:实腹梁的弹性承载力要高于空腹梁;其他条件均相同时,梁B3(6孔,孔长350 mm)的承载力约为梁B2(3孔,孔长800 mm)的2倍,这说明承载力受孔长、孔洞分布的影响较大;其他条件均相同时,梁承载力高低与倒角形式有关,设置等腰直角三角形倒角时最高,设置1/4圆弧倒角时次之,不设置倒角时最低;孔洞长高比对承载力的影响程度要显著高于设置倒角与否。

2.2.2 挠 度

按图4布置位移计,记录梁上各测点在分级荷载作用下的挠度值。5根试验梁在各级荷载作用下实测值、Abaqus模拟值所得的荷载-挠度曲线如图8、图9所示。

空腹梁B2(3孔,孔长800 mm)与B3(6孔,孔长350 mm)除开孔数与孔长不同外其余条件完全相同。由图8可知,空腹梁B2、B3在相同荷载作用下的挠度值明显大于实腹梁B1,梁B2挠度值明显大于梁B3,这说明集中开孔对梁挠度的影响较分散开孔大,并与前述关于承载力的分析一致。

梁B3、B4、B5除倒角形式和是否设置倒角有区别外其他条件完全相同。由图9可知,在相同荷载作用下,无倒角梁B5挠度值明显大于设置倒角的梁B3、B4。实测值和Abaqus模拟值荷载-挠度曲线均体现出梁B3、B4的荷载-挠度曲线非常接近,这说明设置等腰直角三角形倒角与设置1/4圆弧倒角对挠度的影响不大。

按照《钢结构设计标准》[16],楼(屋)盖主梁由永久和可变荷载标准值产生的挠度容许值

(2)

查荷载-挠度记录表,取梁跨中3#测点处挠度f=7 mm时所对应的加载值为F0,5根梁弹性加载值Fe、F0的实测值与Abaqus模拟值见表2。

图8 梁B1、B2、B3的2#、3#测点处荷载-挠度曲线Fig.8 Load-deflection curves at measuring point 2#,3# of beam B1,B2,B3

表2梁弹性加载值Fe与达到挠度容许值时的加载值F0
Table2Fe(elastic loading value) andF0(load value when reaching the allowable defletion value) of each beam

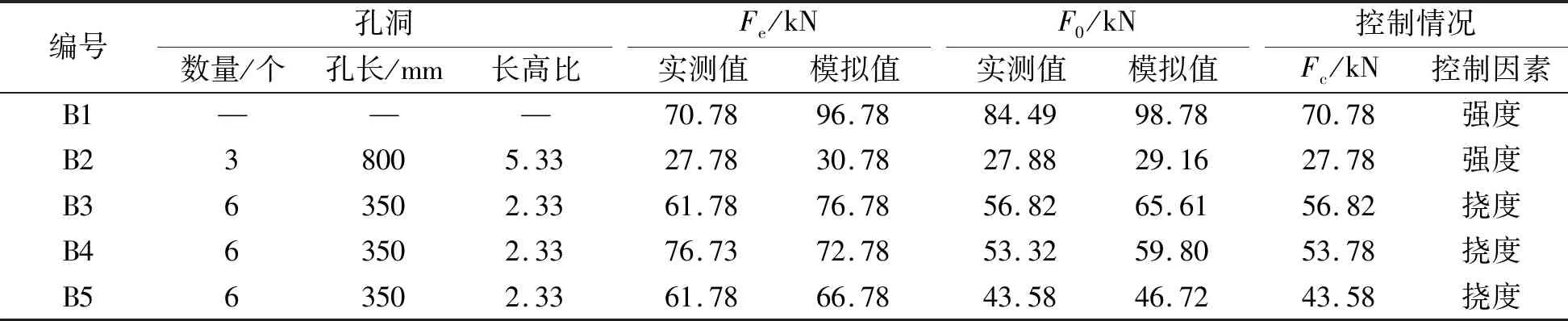
编号孔洞数量/个孔长/mm长高比Fe/kN实测值模拟值F0/kN实测值模拟值控制情况Fc/kN控制因素B1———70.7896.7884.4998.7870.78强度B238005.3327.7830.7827.8829.1627.78强度B363502.3361.7876.7856.8265.6156.82挠度B463502.3376.7372.7853.3259.8053.78挠度B563502.3361.7866.7843.5846.7243.58挠度

由表2可知,实腹梁B1的F0值最大,开孔长度较大的梁B2的F0值最小,梁B3(等腰直角三角形倒角)、梁B4(1/4圆弧倒角)、梁B5(无倒角)的F0值依次减小。梁B3与梁B4的F0值相差不大,这说明设置等腰直角三角形倒角与设置1/4圆弧倒角对梁挠度达到容许值时的承载力影响不大。不设置倒角梁B5与设置1/4圆弧倒角梁B4相比,当达到挠度容许值时,梁B5的承载力比梁B4小20%左右,这说明设置倒角与否对梁挠度的影响较大。

由表2所列的实测值可知,梁B2由强度控制,梁B3、B4、B5均由挠度控制,这说明当空腹梁开孔长度较小,孔洞长高比约为2、孔洞沿梁长均匀分布时,梁的承载力受挠度控制。

如前述,当孔洞设置较为合理时,空腹梁承载力受挠度控制,为便于初步设计时估算梁的抗弯刚度,以挠度容许值为参考,对空腹梁的等效截面惯性矩I值进行分析。按试验方案加载时梁在荷载作用下的挠度

(3)

采用图乘法计算试验梁在荷载作用下的挠度值f，如图10所示。

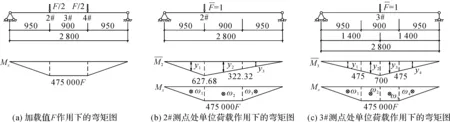
图10 用图乘法计算的梁挠度(单位：mm)Fig.10 Beam deflection calculation by diagrammatic multiplication method(unit: mm)

(4)

(5)

由图10(b)、(c)可得2#(或4#)测点处∑(ωiyi)=345 958 333.3F;3#测点处∑(ωiyi)=394 052 083.3F。

设相邻分级加载值为Fi、Fi+1,与之对应的挠度值为fi、fi+1,本试验Fi+1-Fi=5 kN、E=2.06×105N/mm2,由式(5)可得,2#、4#测点处所对应的梁横截面等效惯性矩

(6)

3#测点处所对应的梁横截面等效惯性矩

(7)

式(6)～(7)中,挠度f的单位为mm,惯性矩I的单位为mm4。

据表2,对梁B1、B2取弹性承载力Fe及与之对应的挠度值fe,对梁B3、B4、B5取挠度容许值及与之对应的承载力F0。以各梁在挠度f=0～7 mm(或fe)区段内各级加载值Fi及其对应的挠度值fi为分析对象,按式(6)、式(7)分别计算各梁在2#(或4#)、3#测点处所对应的梁横截面等效惯性矩I值,再对各梁取横截面等效惯性矩I的平均值(表3)。按实测截面厚度,实腹梁横截面惯性矩理论值为It=29.006×106(mm4)。

表3 梁横截面等效惯性矩平均值Table 3 Mean value of equivalent inertia moment of each beam cross section

由表3可知:梁B1由于加工时梁高沿长度方向的不均匀性、焊接时存在初始翘曲及H型钢的制造误差,使得实腹梁等效I值比理论值偏小;孔洞长高比较大的梁B2受弹性极限状态承载力限制,局部屈曲过早发生,梁的整体性无法充分发挥,等效I值约为理论值的25%,应避免使用,或对薄弱部位采取构造措施加强后使用;梁B5没有设置倒角,其等效I值只有理论值的40%左右,远低于设置了倒角的梁B3、B4;梁B3(设置等腰直角三角形倒角)与梁B4(设置1/4圆弧倒角)的等效I值相差不大,可根据需要选用;对孔洞长高比在2左右,孔洞沿梁长均匀分布的空腹梁,可取等效I值为实腹梁理论I值的55%进行挠度试算。

3 结 论

通过试验结果和数值模拟分析可得出如下结论:1)倒角(无倒角时为抗剪键)与梁肋交接点处为空腹梁的薄弱部位,应重点关注和校核,必要时可采取加强措施。2)孔洞长高比是影响空腹梁承载力的一个重要因素,孔洞长高比取2左右为宜,当孔洞长高比大于2较多时,应对倒角与梁肋交接点处采取构造措施加强。3)空腹梁抗剪键与梁肋交接点处应设置倒角,在相同条件下,当达到挠度容许值时,不设置倒角空腹梁的承载力只有设置倒角空腹梁的80%左右。4)抗剪键与梁肋交接点处设置三角形与圆弧形倒角对空腹梁承载力的影响不大,可根据实际需要选用。5)当空腹梁采取较为合理的构造措施时,如孔洞长高比在2左右、孔洞沿梁长均匀分布、设置倒角等,空腹梁的承载力受挠度控制,可取空腹梁的等效I值为实腹梁理论I值的55%进行挠度试算。