基于卡尔曼滤波的AGV惯性导航仿真研究
2020-07-02王伟博贾兆远韩林廷
袁 斌,王 辉,王伟博,贾兆远,韩林廷
(浙江科技学院 机械与能源工程学院,杭州 310023)
自动引导小车(automated guided vehicle,AGV)作为一种柔性智能搬运设备,在制造车间、快递物流等场所应用越来越广泛,对中国制造业带来重要影响[1]。AGV常见的导航方式有视觉导航、激光导航、磁条导航、惯性导航等。近年由于机器视觉技术的发展,于亦奇等[2-3]提出一种视觉导航,它可以完成粗略的导航定位,但很难满足现实需求。导航精度能满足实际需求的有车菲[4]提出的激光导航和刘娟[5]、李玉琪[6]提出的磁条导航,但它们很难符合目前所提倡的柔性制造。在生产制造中我们既要导航精度也要轨迹柔性,虽然惯性导航兼顾了两者,但它存在无法消除的累积误差,杨玉明[7]针对惯性导航存在的累积误差对AGV机械机构进行改进和导航算法优化,但惯性导航的定位精度在很大程度上取决于惯性元件。为了在短距离室内导航中能使AGV定位达到较高精度且成本较低,本文展开了基于卡尔曼滤波(Kalman filter)[8]的惯性导航研究,将惯性元件解算得到AGV的姿势进行卡尔曼最优估计,得到最优姿势,再通过PID控制(proportional-integral-derivative control,比例-积分-微分控制)进行姿势调节,并且引入偏置量弥补系统存在的未知偏置误差。
1 AGV轨迹误差分析
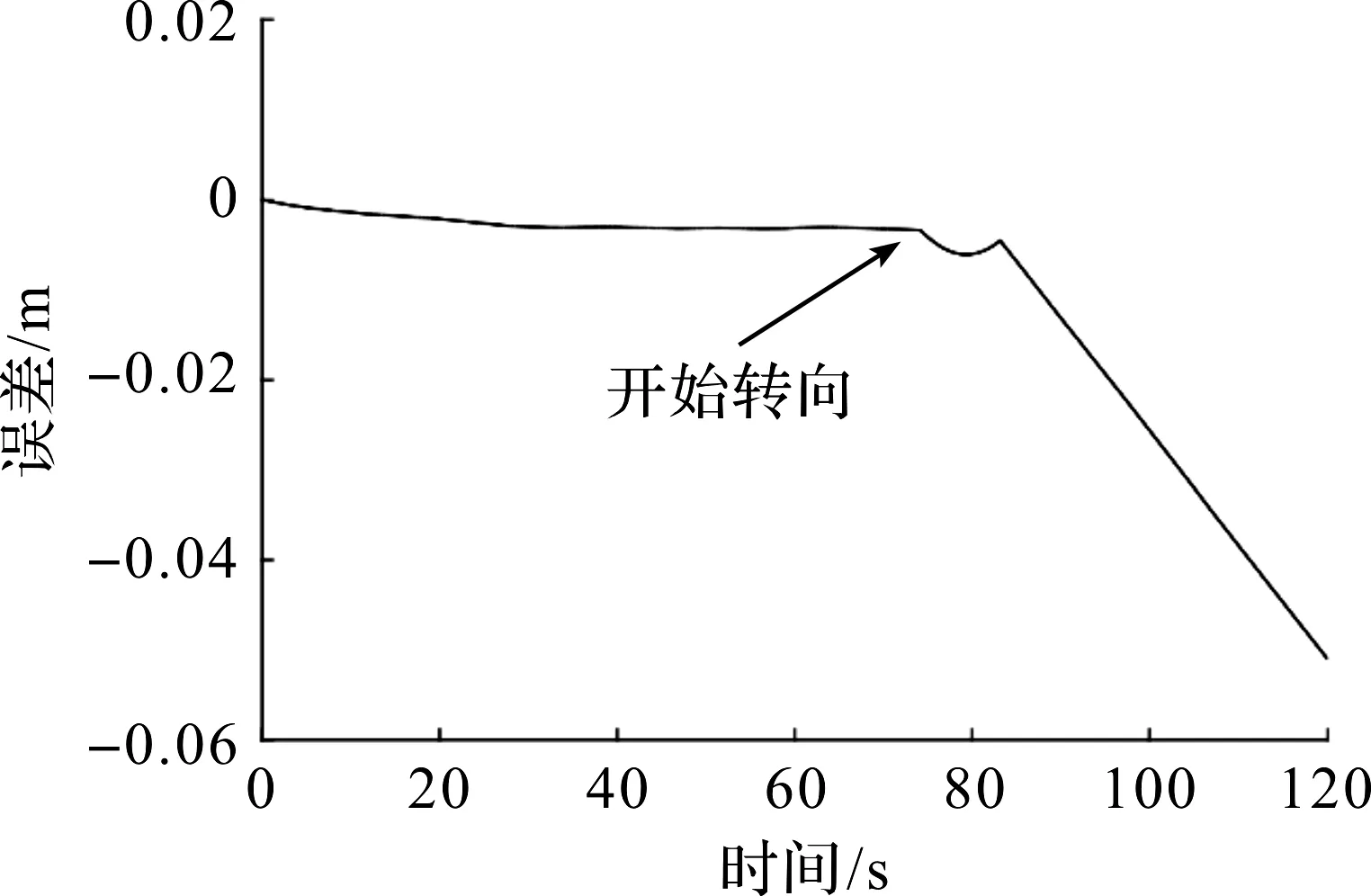
图1 AGV轨迹误差仿真Fig.1 AGV trajectory error simulation
AGV在直线行驶过程中存在累积误差、过程噪声和观测噪声,这些都对AGV的导航产生一定的影响。传统控制方式的AGV在直线运动过程中轨迹误差累积较缓慢,但转向处误差出现突变,由于传统控制方式无法消除累积产生的误差,因此,随着AGV继续运行,误差越来越大。AGV轨迹误差仿真结果如图1所示。
经过Δt时间后,AGV角度误差ωe和轨迹误差de[9]可表示为
(1)
式(1)中:Δω为角度误差增量;VL、VR为左右轮线速度;L为两轮之间距离;Δd为轨迹误差增量。
根据图1和式(1)可知,当转角存在误差时,转角误差对后续轨迹运动影响较大,基于此,开展基于卡尔曼滤波定位及转角滤波研究,对AGV姿势进行实时最优估计并及时调整姿势。
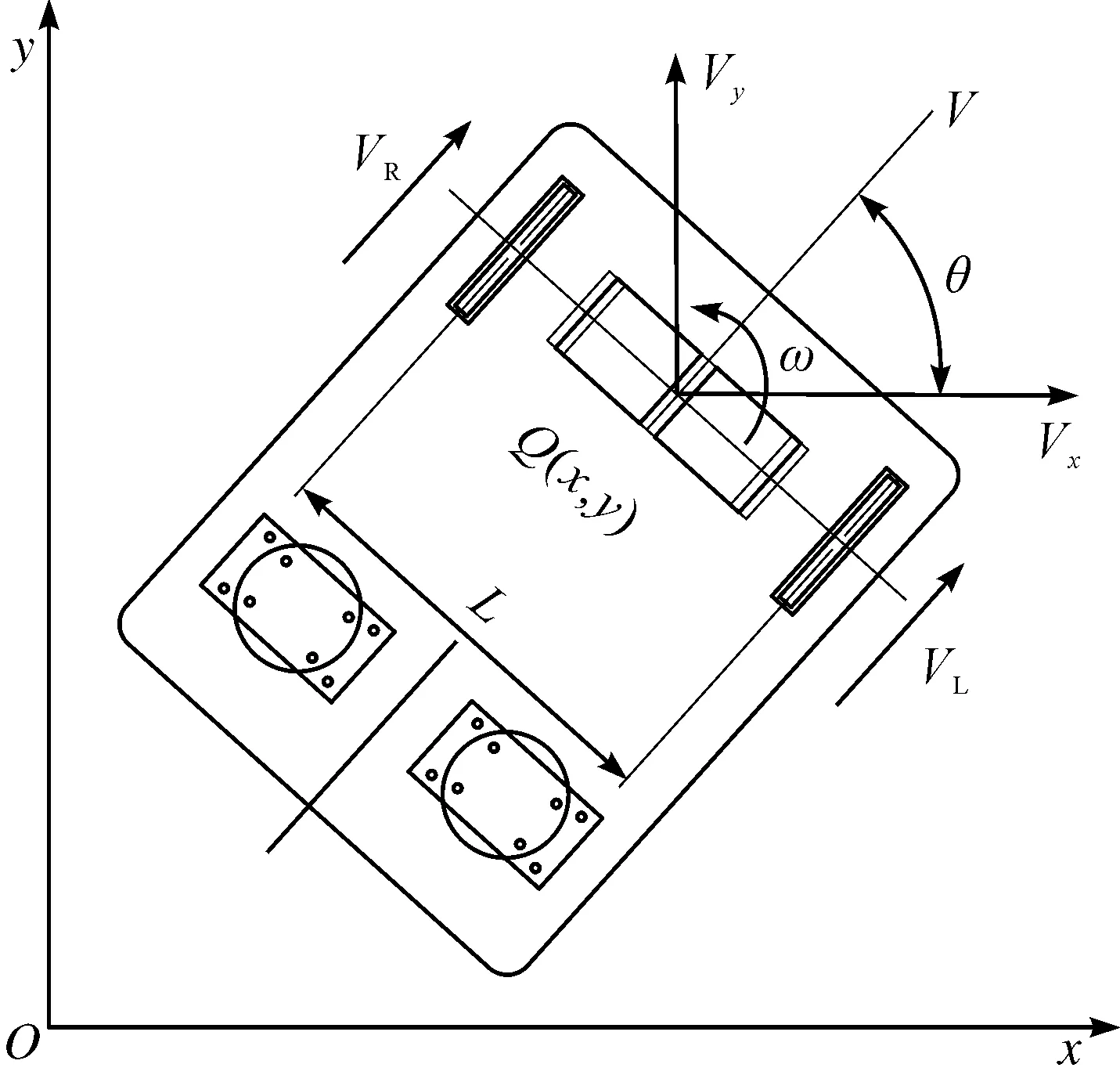
图2 AGV运动模型Fig.2 AGV motion model
2 AGV定位纠偏控制模型
2.1 AGV运动学模型
AGV在行驶过程中,由卡尔曼滤波算法对AGV姿势做出最优估计,从而得出最优姿势,并发送给控制器,控制器通过脉冲宽度调制(pulse width modulation,PWM)控制电机驱动器,从而控制电机调整AGV姿势。本研究建立如图2所示的AGV运动模型。
AGV在Q点坐标为(x,y),转角为θ,因此Q点姿势Q可以表示为[x,y,θ]T。AGV采用差速轮驱动,左右两轮线速度VL、VR可以由电机转速nR、nL表示为
(2)
AGV的线速度V和角速度ω定义如下:
(3)
AGV姿势Q离散化后表示为
(4)
式(2)~(4)中:r为轮子半径;T为采用周期;ux(k)、uy(k)、uθ(k)分别为x、y、θ的控制量。
2.2 惯性系统误差及卡尔曼滤波定位原理
由于惯性元件的误差会随时间变化,严重影响惯性导航在AGV上的应用发展,因此,我们需要分析、估计误差。惯性元件主要由陀螺仪和加速度计组成,陀螺仪是一种角运动元件,它的准确性对AGV的转角产生直接的影响。陀螺仪的误差主要由刻度系数误差和漂移组成,刻度系数是一个随机常数,可通过标定消除,因此,陀螺仪误差[10]333、加速度计误差[10]334(主要包括偏置误差和随机误差)可以表示为
(5)
式(5)中:εbi(t)为逐次启动漂移;εri(t)为慢变漂移(可忽略);ωgi(t)为陀螺仪白噪音;βbi为偏置误差;ωai为加速度计白噪音。为了简化误差模型可以将惯性元件误差看成白噪音和偏置误差组成。
从表1看出,油研11号在钾肥施用量为20公斤/亩时的产量最高,达210.09公斤/亩,以不施钾肥处理的产量最低,为194.57公斤/亩。而三北98则是钾肥施用量为25公斤/亩时的产量最高,为205.3公斤/亩,不施钾肥和施用5公斤/亩钾肥处理的产量较低,两者相差不大。方差分析表明,品种间和处理间产量差异均未达显著水平。各处理产量平均油研11号为200.67公斤/亩,三北98为201.12公斤/亩。
为了消除惯性元件的偏置误差,在观测上引入偏置,AGV在动态过程用一般隐马尔科夫模型(hidden Markov model)表示出系统状态A和观测值Z:

(6)
式(6)中:F为状态转移矩阵;Γ为噪声驱动矩阵;W为过程噪声;H为观测矩阵;V(k)为观测噪声;b(k)为测量偏置。
在观测方程中引入测量偏置并利用逆威沙特(normal-inverse-Wishart)分布拟合估计出偏置值[11]。卡尔曼滤波算法主要包括预测和更新两个过程,预测根据上一次状态和控制量进行预测,更新根据本次状态和传感器数据进行高斯混合(Gaussian mixture)得到最优数据。卡尔曼滤波式子[12]36如下:
(7)
最后将经过卡尔曼滤波的角速度进行四元数解算,可以将翻滚角φ、俯仰角θ、偏航角ψ[13]用四元数表示如下:
(8)
通过一阶龙格库塔法(Runge-Kutta)迭代,可以将惯性元件测得的角速度来表示四元数,从而求得欧拉角(Euler angle):
(9)
式(8)~(9)中:q0、q1、q2、q3为四元数;ωx、ωy、ωz分别为三个方向的角速度。
为了便于观察AGV的定位误差,在MATLAB软件中进行直线行走和转弯的仿真。图3为卡尔曼位置观测及误差,图4为卡尔曼角度观测及误差。
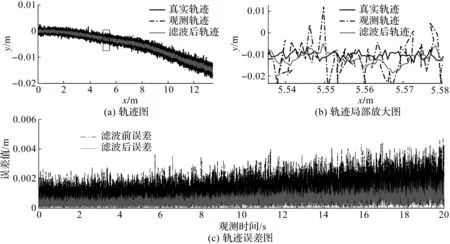
图3 卡尔曼位置观测及误差Fig.3 Kalman positioning observation and error

图4 卡尔曼角度观测及误差Fig.4 Kalman angle observation and error chart
2.3 AGV纠偏模型建立
通过MATLAB中的Simulink建立AGV纠偏控制模型,如图5所示。模型主要由AGV控制器模块、直流无刷电机模块[14]、姿势解算模块、卡尔曼滤波器模块[12]160和其他模块组成,并且电机控制采用MATLAB中的power_brushlessDCmotor模块为基本单元。AGV在运行过程中,卡尔曼滤波器采集惯性元件的数据进行最优估计,然后将最优姿势与控制器的目标姿势进行比对得到偏差,最后通过PID控制器调整AGV姿势。
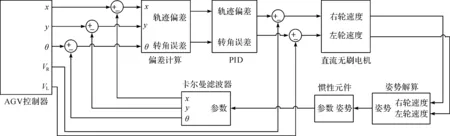
图5 AGV纠偏控制模型Fig.5 Control model of AGV correction
3 仿真与结果分析
3.1 模拟AGV转弯运动数据
AGV小车先匀速直线行驶,然后进行90°转弯。模拟直线行驶距离为10 m,转弯后再行驶3 m。AGV行驶速度、方向角初始值都为0。模拟运动局部轨迹如图6所示,其行驶轨迹误差如图7所示。
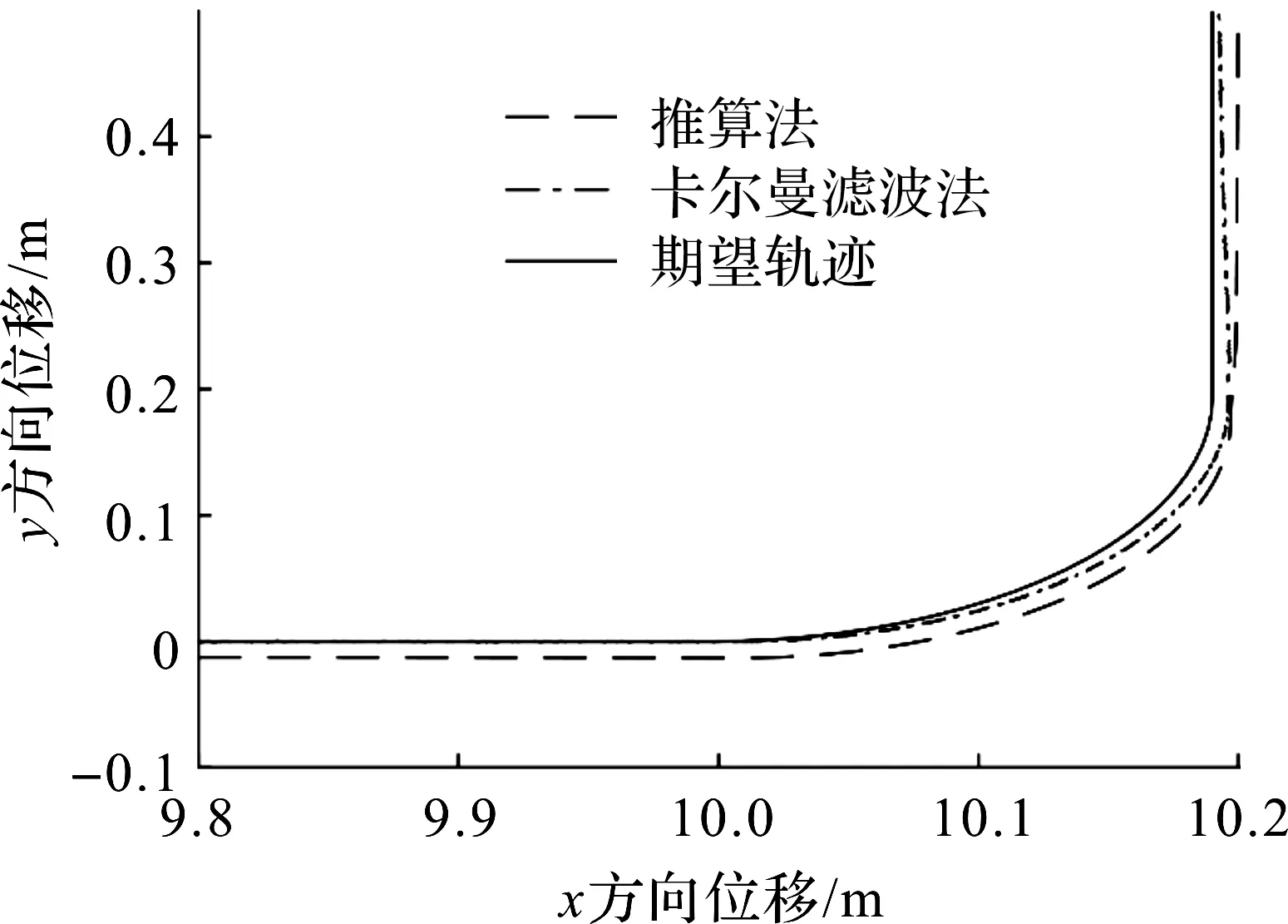
图6 模拟运动局部轨迹Fig.6 Local trajectory of simulation motion
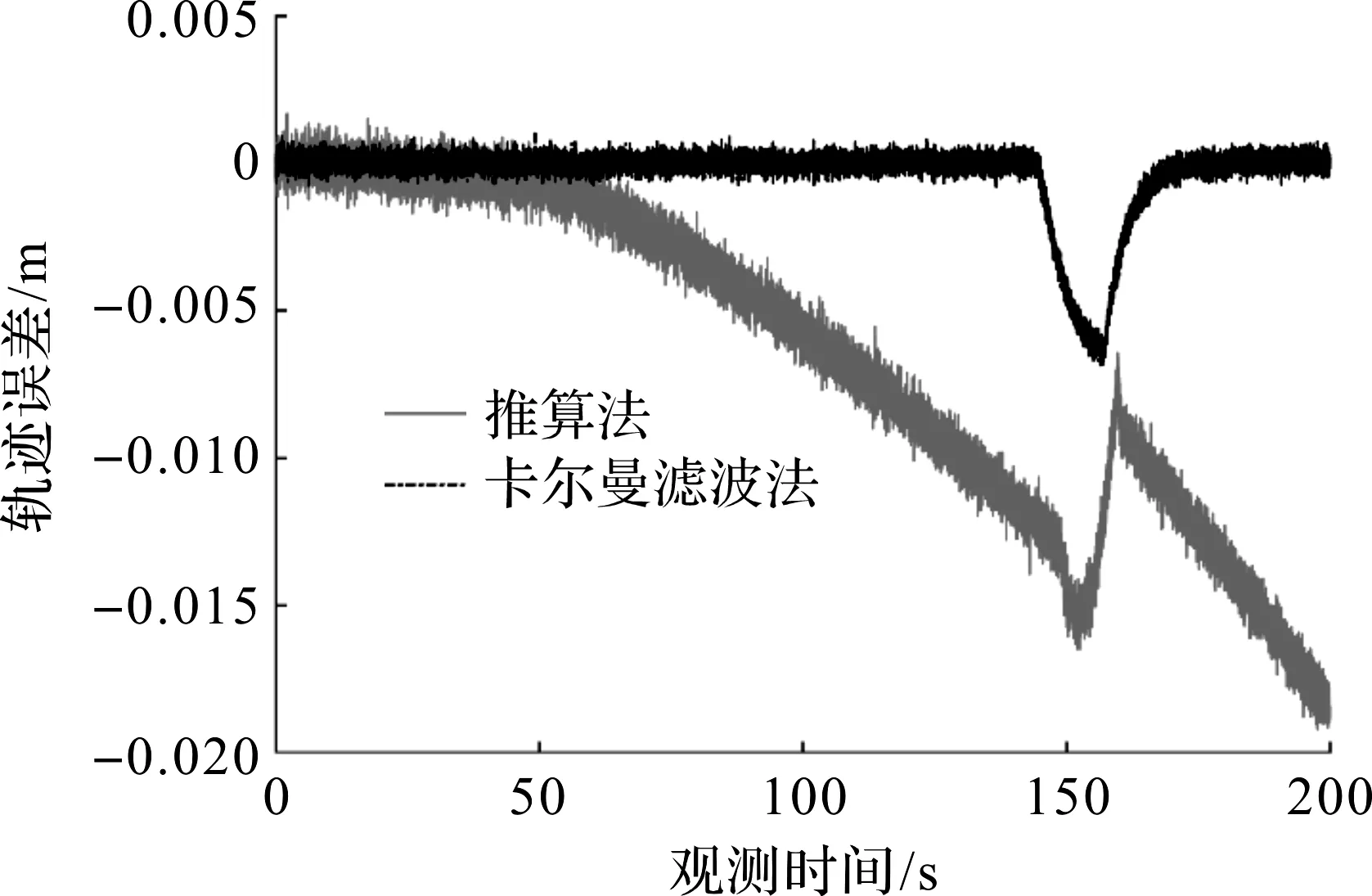
图7 AGV轨迹误差Fig.7 AGV track error
3.2 结果分析
通过两种控制方式的仿真比较,经过计算得出,在短距离内卡尔曼滤波定位惯性导航方式的轨迹均值误差为0.000 58 m,而传统推算法为0.004 69 m,前者导航精度比后者提高了8倍左右。
AGV在运动过程中由于两轮转速存在偏差,需要不断调整自身姿势。由于卡尔曼滤波算法具有较好的实时性,因此,对于控制量频繁改变的AGV具有较好的适应性。
4 结 语
卡尔曼滤波定位惯性导航方式控制简单、实用,在一般场所中能满足所需的精度和稳定性要求。本文通过在惯性导航中加入带偏置的卡尔曼滤波进行轨迹预测和角度滤波,提高了惯性导航的室内定位导航能力,通过Simulink仿真验证了这一方法的有效性,从而为AGV的定位导航问题提供了一定的理论参考。
