早期预警信息解算方法探究*
2020-07-02汪东海周智亮刘伯阳田志宇
汪东海,周智亮,刘伯阳,田志宇
(1.中国人民解放军63611部队,新疆 库尔勒 841000;2.中国人民解放军63610部队,新疆 库尔勒 841000)
0 引言
关于早期预警雷达相关技术研究成果,从国内各个学术期刊数据库中检索中,可以发现研究人员的主要研究方向是早期预警雷达部署[1-2]、预警信息处理系统[3]和雷达数据融合[4],但是对于从早期预警雷达跟踪数据中进一步提取的具体预警信息没有详细论述。早期预警信息要实现战略预警的功能,应满足如下2个特性:①实时性,即若有导弹或者飞机侵入我方领空,应立即发送预警信息,这个要求预警雷达应实现全天24 h战备值班和数据解算应该保证实时性;②预警信息内容尽可能全面和详细,为指挥员做出准确地防御和攻击计划提供数据依据。本文主要探讨利用早期预警雷达跟踪定位弹道数据完成对来袭目标的精确定位,并利用定位弹道信息实时计算出早期预警信息相关方法。
1 早期预警信息及解算过程
通过靶场不断地摸索试验,早期预警信息一般要包括以下几个要素:来袭导弹的发射点经纬度、发射时间、发射射向、导弹发动机是否关机、落点的经纬度和时间。早期信息解算是有一个数据处理流向过程,如下图1所示,首先要对雷达测得的四元素(时间T、测距R、方位角A、俯仰角E)中的测距R和俯仰E进行电波折射修正[5-6]、测元检择、针对非线性系统采用不敏卡尔曼滤波(unscented Kalman filter,UKF)进行滤波处理并完成对目标状态估计,对获取的弹道位置、速度进行数据积累和拟合平滑处理。然后将平滑处理后的地心地固坐标系下的7个参数值弹道值(t,x,y,z,vx,vy,vz),作为解算早期预警信息输入值。在导弹发射起始阶段,存在多次机动加速,综合考虑到数据处理模型的解算的实时性和精确度问题,本文选择较为成熟的CS-UKF滤波模型,下一节将具体介绍。

图1 早期预警信息解算过程Fig.1 Process of early warning information
2 弹道估计
导弹在主动段火箭推力情况复杂,且先验弹道轮廓信息很少,为建立精确的导弹目标运动模型带来了极大的困难。机动目标建模不仅是滤波器的重要组成,也是从运动学机理上解决目标机动问题的方法。关于几种机动目标模型优缺点比较,可以参考文献[7],本文状态方程采用运动学建模,选择基于“当前”统计(current statistical,CS)模型。
2.1 CS模型
关于“当前”统计(CS)模型[8-9]是我国学者周宏仁在Singer模型的基础上提出的一种统计模型。该模型采用非零均值和修正瑞利分布来表征机动加速度的特性,因而更加切合目标的实际机动情况,是目前较好的实用模型。该模型用修正的瑞利分布来描述机动加速度的“当前”概率密度,均值为“当前”加速度预测值,随机加速度在时间轴上仍符合一阶时间相关过程,即

(1)

(2)


(3)
(4)
将式(3)和式(4)写为状态方程,即为CS模型:


(5)
2.2 UKF滤波
在使用“当前统计”目标机动模型使得在计算过程中呈现非线性,而不敏卡尔曼滤波器(UKF)可以很好地解决这种非线性问题,它是对状态向量的概率密度函数(PDF)进行近似化,表现为一系列选取好的δ采样点。这些δ采样点完全体现了高斯分布的真实均值和协方差。当这些点经过任何非线性系统的传递后,得到的后验均值和协方差都能够精确到二阶(即对系统的非线性强度不敏感)。由于不需要对非线性系统进行线性化,并可以很容易地应用于非线性系统的状态估计。

(6)
i=1,2,…,nx,
(7)

3 关键要素计算方法
目前实际数据处理应用中无论发射点估计,还是落点估计[11],或者导弹关机状态判别,均使用四阶龙格库塔积分方法,它是用于非线性常微分方程的解的重要的一类隐式或显式迭代法。通用的积分方法模型,可用下述几个公式进行描述:
(8)
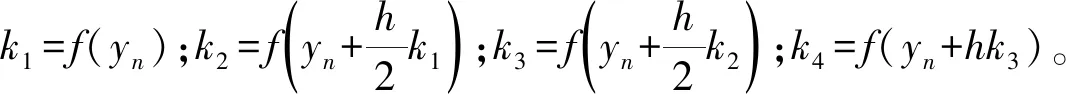
需要说明的是积分弹道位置和速度所用函数f(yn)不同。以第n点x方向的位置和速度分别为例,则函数可表示为
f1=hg1(xn),
(9)
f2=h[g2(xn,yn,zn)+g3(xn,yn,zn)+
g4(xn,yn,zn)],
(10)
式中:g1为为第n点x位置对应的速度函数;g2为第n点对应空间位置在x方向的引力加速度函数;g3为第n点对应空间位置在x方向由地球自转引起的哥氏加速度函数;g4为第n点对应空间位置在x方向由地球自转引起的牵连加速度函数。若考虑空气阻力的影响,则需要引入3个方向的空气阻力加速度,式中h代表是积分步长,其他方向类似。在主动段还受火箭推力和控制力影响,受力情况复杂难以建模,一般采用运动学模型建模。在自由段空气阻力加速度可以不考虑。
3.1 发射点经纬度及发射时间
发射点信息精准计算是一个难点问题,弹道导弹先是垂直起飞,达到一定高度进行程序转弯向预定射向飞行,而通过预警雷达测量弹道一般是程序转弯之后的弹道,因此是无法判别程序转弯点在具体哪个空间位置点上。对于给定一段弹道,反向计算发射点位置会有很多种可能性。提高发射点计算精度方法,在于预警雷达能否尽早跟踪到弹道导弹主动段飞行过程,越早跟上发射点经纬度及时间估算就越准确。
通过接收一段早期预警雷达测量弹道,来计算发射点信息,目前采用方法是对雷达测量数据按照本文第二节介绍内容进行相关预处理,获取跟踪目标的弹道值(t,x,y,z,vx,vy,vz),以该弹道作为积分初值进行龙格库塔逆向积分直至地面(或者逆向积分到一定高度后,进行地面投影),将积分后弹道进行坐标转换到大地系,即获取发射点经纬度以及发射时间。记录每一次的积分步长-hi,每积分一次,t=t-hi,当出现过零点时,t=t+86 400。如果具备完整的地球表面地理信息数据支持,可对发射点海拔高度做出估计,同时可提高经纬度参数估计精度。在雷达跟踪稳定及弹道估计比较平滑后,应该尽早固定估计的发射点参数,这个主要因为用时间靠后累积的弹道进行计算,精度会变得更差。
3.2 发射射向
发射射向采用东北天坐标系(ENU),以发射点为视角得到的导弹发射射向,其解算不涉及到速度和加速度参数计算,只需要知道目标地心地固系下2点的位置弹道坐标值即可。发射射向解算问题,可以概括为:2点地心系A(tA,xA,yA,zA),B(tB,xB,yB,zB),计算A→B方向的发射射向Φ。首先要对2点地心系坐标做大地系转换[2],假设转换后A,B2点的大地系坐标(经、纬、高)分别为A(LA,BA,HA),B(LB,BB,HB),在选取2点的时间间隔上一般要求大于10 s,若2点离得太近会导致每个点的位置误差引起计算发射射向有较大的偏差。公式(11)给出了初始射向A的计算方法:
(11)
式中:
cosc=sinBBsinBA+
cosBBcosBAcos(LB-LA).
发射射向因采用的东北天坐标系,它的值范围为[0,360),对于求出初始射向A的弧度值还需进行区间检择,才可以得到发射射向Φ的值。当BA≥BB时,Φ=180°-A;当BA 对弹道导弹关机状态的判断正确与否,影响着弹道预报准确性,若导弹已经关机,则导弹飞行轨迹只受重力方程约束,基于某一点精确估计的弹道参数进行弹道积分,可以获取精度较高的预报弹道及落点信息;若导弹未关机,则仍受到推力影响,预报弹道与实际飞行弹道误差很大。特别是针对多级导弹,判断各级关机点时间会变得更加困难。 若雷达测量数据精准且误差扰动较小,则可以通过2个参数共同判断:①合加速度值进行判断,下图2为某型号导弹关机之后的GPS数据计算出的合加速度值,可以看出加速度范围在10 m/s2以下,加速度最低点便是弹道最高点位置,程序解算时,合加速度值可以放宽为9.8±1 m/s2这个范围;②要对y方向的加速度值或者z方向的加速度值是否为负值进行判断,自由段飞行时,这2个方向的值均为负,即导弹合加速度处于9.8±1 m/s2这个区间且y方向或者z方向的加速度值为负,则可认为导弹已经处于关机状态。 然而在实际跟踪过程中,雷达在导弹动力飞行段,特别是导弹关机点前后,跟踪测量数据精度较差,且很难连续稳定跟踪,估计的弹道各方向速度和加速度误差很大,此时拿加速度值做导弹关机判断条件错误概率很大,因此考虑不通过加速度和速度具体数值来进行判断,而只是通过加速度和速度值的正负性来进行判断。图3为导弹飞行阶段的曲线图,仔细观察图型可以将导弹飞行阶段划分成4个阶段:动力飞行段、关机点阶段、自由上升阶段和自由降落阶段。 图2 合加速度曲线Fig.2 Curve chart of combinatorial acceleration 图3 导弹飞行阶段Fig.3 Curve chart of missile trajectory stage 这4个阶段可以用滑窗积累各个点的合加速度和z方向加速度值的正负来唯一确定,数据实时处理软件在应用上也很容易实现。如表1所示,其中a1,a2,…,an为数据滑窗中每个点对应的合加速度,az1,az2,…,azn为数据滑窗中每个点对应的z方向的加速度值。 表1 全程弹道特点Table 1 Full-course trajectory characteristic 对于导弹是否关机,还可通过弹道预报曲线进行直观判断。图4为每次向后预报20个弹道点,每个点相隔10 s,总共向后预报200 s弹道情况。这种弹道预报模式对每一次预报采用弹道初始值精度要求非常高,尤其是对速度要求异常苛刻,上述的CS-UKF滤波模型是不合适作为弹道预处理的方法,只能采用高精度弹道预报模型[12]才可以。按照自由飞行段动力学模型对弹道进行外推并画出各个时间点的预报弹道,结果若导弹已经关机,则2次预报弹道曲线是大部分重合在一起的;若导弹仍处于主动飞行段,上一次预报点数组成的曲线和下一次预报点数组成的曲线没有一点重合。图4画出的曲线图为用某次导弹飞行时实时预报的结果,可以看出没有关机时预报终点位置相差较大,各预报曲线成散开状,关机之后,曲线重叠在一起,如图4深蓝色曲线所示。 图4 弹头预报曲线Fig.4 Curve chart of warhead forecast 落点经纬度及时间的3个参数估计是基于弹道导弹关机之后,进行弹道积分外推预报,外推的方法仍采用四阶龙格库塔数值积分法,积分外推到地面。利用早期预警雷达跟踪测量数据进行落点预报有一定局限性,主要有以下2个方面的原因:①弹道导弹再入段飞行,除了自由段所考虑受力情况还受空气阻力和高空风影响。目前虽然有较好的空气阻力模型,但是阻尼系数的计算和估计存在一定困难,不能实时获取高空气象参数,且获取气象参数高度有限、代价较高;②现在的弹道导弹会有末端机动,来突防对方导弹拦截系统,若只用上述的落点预报方法,会有很大误差。因此早期预警中,落点经纬度及时间的预报只能作为参考值,要实现落点准确预报,需要末端预警雷达实时跟踪,并采用相应处理方法[13-15],将捕获到导弹弹道数据进行分析处理才行。 早期预警雷达是建立预警系统不可缺少的地基传感器,本文详细叙述了从早期预警雷达原始数据中提取早期预警信息要素、处理早期预警信息过程,及各个要素处理方法,对预警系统建设中雷达数据实时处理有一定帮助和指导意义,要想获得更高精度早期预警信息,还需要不断从敌方武器本身特点、雷达传感器性能指标及预警中心数据处理方法等方面摸索出制约因素,建立更优化的模型。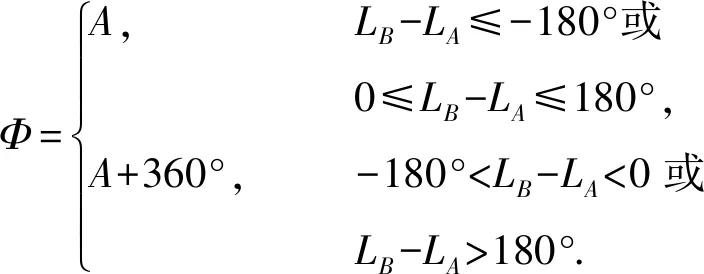
3.3 导弹关机状态




3.4 落点经纬度及时间
4 结束语
