相邻优属度熵权在地面防空部署评估中的应用*
2020-07-02张文博李孝军张景盛
张文博,李孝军,张景盛
(空军工程大学a.研究生院;b.防空反导学院,陕西 西安 710051)
0 引言
防空部署是各级指挥员对防空作战力量的任务区分、力量编组和配置作出的安排,是防空作战决心的重要内容[1]。科学合理的防空部署,能够充分发挥防空兵力、火力的效能,能够满足不同情况、战法的需要。在实际作战中,防空部署受空袭威胁、阵地条件、兵力情况、掩护目标等多因素限制,而且有些因素又具有相当的不可控性,对防空部署的影响具有一定程度的随机性和模糊性,因此,如何贴近地面防空作战的实际需求,对部署方案进行全面、客观、准确地评估,在众多部署方案中进行科学有效地优选,一直是防空作战中亟待解决的难点。
目前,对于地面防空部署方案的评判有两类方法:一类如文献[2],将部署指标分为动、静态指标,以静态指标为约束条件、动态指标为目标函数,利用多目标规划的方法评价;另一类,对多因素进行赋权转化为单目标求解,在对各因素权重进行确定时,多采用主观赋权的方法,如在文献[3-5]采用多属性决策、层次分析法、德尔菲法等主观方法确定权重。前者往往求解困难,后者由于主观赋权受主观人为因素影响多,导致所得权重结果主观性大,影响评价方案的真实性和可靠性,若仅仅采用客观赋权的方法,会受到样本随机误差影响,也不能很好地反映指挥员的主观倾向。鉴于此,本文提出基于相邻优属度熵权确定权重的方法,将专家的主观赋权与数据样本得出的客观权重相结合,利用二级模糊综合模型评判,能较好地实现对防空部署方案进行评判优选。
1 地面防空部署方案评估指标体系构建
防空部署体现的强对抗性、多约束性,决定了确定部署方案是一个多因素共同作用影响的过程。防空部署主要考虑的因素包括:上级的作战意图、地空导弹武器的数量和性能、杀伤区的重叠、易受攻击区、地域特征、对抗干扰、被掩护对象性质和面积、与其他防空武器配合、射击后转移等。因此,在分析部署方案时,需要多维度设立指标,依据简单性、独立性、完备性、客观性将因素进行归类。在借鉴前人的研究成果基础上,本文提出采用符合上级意图、抗击效率、自身生存能力、方案易行度4个主要指标构建指标体系。符合上级意图,反映防空部署方案符合上级最基本部署指标要求的程度;抗击效率,综合反映抗击空袭兵器突防的概率,防空部队对要地保卫的情况;自身生存能力,反映地面防空部队在对抗中生存能力的大小;方案易行度,反映部署方案在实际作战中执行的难易程度。具体的指标体系如图1所示。
对于指标的量化,前人已做过大量工作,如在文献[4-7]中对部署火力区大小、杀伤区重叠次数、火力密度等都已做了研究。对于定性指标,可采用多级比例法等进行量化,在此不再赘述。
2 防空部署评估优选方法
2.1 两级模糊综合评判模型
由于防空部署影响因素较多,若采用一层模糊综合评价模型,各因素的相对权重会偏小,会与隶属度矩阵不匹配,容易造成评价出现模糊现象,结果区分率差,因此,采用两级模糊综合评判。

图1 地面防空部署方案评价指标体系Fig.1 Evaluation index system of ground air defense deployment scheme
(1) 评语集与因素集确定
评语集V表示对部署指标效果等级划分的集合,V={vj},j=1,2…,m。可将防空部署的效果分为5级:差、一般、较好、很好、极好,分别用Ⅰ,Ⅱ,Ⅲ,Ⅳ,Ⅴ表示。即:V={Ⅰ,Ⅱ,Ⅲ,Ⅳ,Ⅴ}。
因素集U表示评价因素的集合U={ui},i=1,2,3,4。ui为一级因素,又可将其划分为相应的子因素ui={uik},k=1,2,…,ni,Uik为ui中的二级子因素。
(2) 模糊评价矩阵确定
模糊集合是通过隶属度函数来表达的,隶属度函数表达形式不唯一,没有统一规律可循。隶属度函数的确定方法众多,常见方法有:集合套法、样板法、模糊统计法、相对比较法、带信任度的德尔菲法、构造隶属函数的参考函数法等[8]。在对防空部署方案数据分析的基础上,选用梯形分布作为隶属度函数,通过将各因素数据代入,计算模糊评价矩阵R。对于评价标准值越来越大的参数选用偏大型函数,即式(1);标准值越来越小的选用偏小型函数,即式(2)。
(1)
(2)
(3) 模糊综合运算及结果分析
在进行评估运算时,首先从每个因素集ui的子因素层进行评估,模型为
bi=W∘ri,i=1,2,3,4,
(3)
式中:“∘”取第Ⅳ类模糊算子M(.,+);W为ui中各子因素的权重集;ri为ui中各子因素对评价语集V的模糊关系矩阵;bi为得到的最底层因素的模糊评价结果集,也构成了上一层因素集ui的评语等级隶属度,各bi构成ui层的等级评价矩阵R=(b1,b2,b3,b4)T。然后再对ui层进行模糊综合评判,可以得到最终评价结果B,即:B=W*R,式中W为U中各ui的权重集。
评价结果B表示部署方案对各等级模糊子集的隶属度,采用最大隶属度原则即可对部署方案的等级作出评判。为了对部署方案进行优选,可对评价等级赋予相应分值,进一步对B处理,计算每个部署方案的综合分值,依据各方案得分大小可完成对部署方案的优选。
2.2 基于相邻优属度熵权的权重确定
2.2.1 相邻优属度确定主观权重
基于相邻目标相对优属度的权重确定方法,是在有限二元比较法的基础上提出的一种求取权重的方法。该方法克服了层次分析法两两比较的缺陷,但需要专家给出相邻目标的相对重要性的排序,本质上是一种主观赋权法。相邻优属度确定权重的步骤[9-12]:
第1步:对目标集O={o1,o2,…,om}中m个评估指标进行重要性降序进行排序,假设o1≻o2≻…≻om。
第2步:定义当ok≻ol时,βkl=1;Ok=Ol时,βkl=1;特别自身比较时,即βkk=0.5,且βlk=1-βkl,其中,k,l=1,2,…,m。考察βk,k+2与βk,k+1及βk+1,k+2之间关系,可得出统一递推公式:
βk,l=βk,l-1+2(1-βk,l-1)(βl-1,l-0.5).
(4)
第3步:求指标相对重要性的有序二元比较矩阵。可由相邻指标的相对重要性模糊度值,求得任意2个指标的相对模糊度值。从而,得到指标相对重要性的二元比较矩阵:
矩阵β的每行之和(不含自身比较)代表指标相对重要性,进行归一化:
(5)
得到指标权重向量:W=(w1,w2,…,wm)T。
2.2.2 熵权确定客观权重
熵的概念来源于热力学,后被应用于信息论中反映系统的无序程度、数据提供的有效信息量。运用信息熵确定权重的基本思想:当信息熵小,反映评价对象在该项指标上提供的有效信息量大,指标的权重应该大;反之,信息熵大,则该指标的权重应该较小。熵权确定的是客观权重,是在客观的信息中得到各指标的权重信息。熵权法确定客观权重步骤[13-15]:
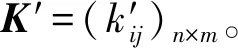
当指标为效益型指标时:
当指标为成本型指标时:
第2步:计算第j个评价指标熵值
指标熵值的定义为
(6)
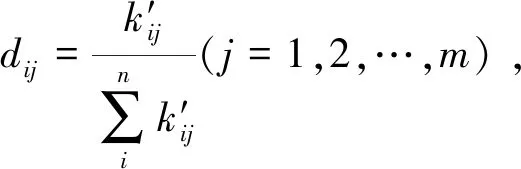
第3步:求第j个指标的熵权
(7)
即各指标的权重集θ={θ1,θ2,…,θm}。
2.2.3 综合权重

(8)
此方法确定部署指标权重的优点在于,即能体现指挥员主观意志,又能较好地反映部署各指标客观信息。
3 实例分析
现针对某次地面防空作战筹划中提出的4个部署方案进行评估,从中选出部署效能最好的方案。表1为对4个部署方案在筹划软件上数据的采集,其中对生存能力、方案易行度等指标请10位专家打分,并进行无量纲化和归一化处理。

表1 部署方案原始数据Table 1 Deployment schema raw data
3.1 指标组合权重的确定
(1) 计算二级指标权重
第1步:计算主观权重。根据专家意见,符合上级意图U1下的各因素重要程度排序为:u11≈u13≻u12≻u14,对其作相邻指标的重要程度比较认为,u11与u13基本同样重要,u13比u12稍微重要,u12比u14较为重要。根据表2语气算子得相邻指标相对重要性模糊度值:β12=0.5,β13=β23=0.6,β34=0.8,则二元比较矩阵

表2 语气算子与模糊标度值对应关系表Table 2 Corresponding relation between mood operator and fuzzy scale value

同理可对抗击能力、生存能力、方案易行度因素集求得各子因素的权重集。抗击能力U2下的各因素重要程度排序为u23≻u21≻u22,认为u23比u21稍微重要,u21比u22较为重要,求得各因素主观权重集w2=(0.377 8,0.191 1,0.431 1)。生存能力U3下的各因素重要程度排序为u32≻u31,认为u32比u31较为重要,求得各因素主观权重集w3=(0.35,0.65)。方案易行度U4下的各因素重要程度排序为u42=u41,比较认为u42与u41基本同样重要,求得各因素主观权重集w4=(0.5,0.5)。
第2步:计算客观权重、综合权重。对原始数据矩阵K进行处理。注意方案易行度因素为成本型指标,全都归一化处理成在[0,1]上的效能型指标,得到矩阵K′。


分别对符合上级意图因素集U1、抗击能力因素集U2、生存能力因素集U3、方案易行度因素集U4归一化处理,利用式(6)~(8)计算熵值、熵权、综合权重,计算结果如表3。

表3 二级因素权重计算结果Table 3 Calculation results of secondary factor weight
(2) 计算一级指标权重
再次利用相邻优属度熵权计算一级指标权重。根据专家意见,对一级指标因素重要程度排序为:U1≻U2≻U3≻U4,比较认为:U1比U2,U2比U3都是稍微重要,U3比U4较为重要,并进行计算主观权重。将各一级因素Ui的子因素的综合权重计算结果作为一级因素计算客观权重的原始数据,如表4,使用相同方法计算出各一级因素Ui的主观权重、客观权重、组合权重列入表5。

表4 部署方案一级指标计算熵权数据Table 4 Entropy weight data calculated by first-level indexes of deployment plan

表5 一级指标因素权重Table 5 Weight of level-1 index factors
3.2 计算模糊关系矩阵
根据表6部署因素分类评价标准,将样本原始数据矩阵K代入式(1),(2)计算得各因素集的模糊综合评价矩阵,进行模糊综合评判。下面以方案S1为例,进行二级模糊综合评判:
(1) 计算方案S1的二级模糊评价b1j
b11=[0.184 3,0,0.113 8,0.470 4,0.231 5],
b12=[0,0.141 7,0.817 5,0.040 8],
b13=[0,0,0.741 9,0.258 1,0],
b14=[0,0.708 5,0.291 5,0,0].
(2) 计算方案S1的一级因素的模糊评价B1
B1=W*R=[0.024 1,0.159 1,0.615 8,
0.170 8,0.030 2].
同理可对部署方案S2,S3,S4进行二级模糊综合评判,可得
B2=[0,0.261 7,0.494 0,0.140 8,0.103 5],
B3=[0,0.303 7,0.439 5,0.087 7,0.169 1],
B4=[0.024 1,0.207 9,0.408 6,0.251 2,0.030 2].
Bi表示每个部署方案对评判等级隶属程度的描述,根据最大隶属度原则可以得出各部署方案等级评判都为Ⅲ级,从结果Bi中也可看出各部署方案的部署特点。如方案S1,S4在Ⅰ级上有分布,表明部署指标上有明显部署短板,S2,S3各项部署指标在Ⅰ级上没有分布,各部署指标都在一般以上,部署得比较均衡。
为了进一步对部署方案优选,可以对每个评价等级赋予参考分值(见表7),进行加权求和计算每个部署方案的得分,根据得分结果对部署方案进行排序优选。从表8可以看出,方案S3为最优的部署方案,这与指挥员的主观判断一致:方案S3各项部署指标都集中在Ⅱ级以上,部署上没有突出的短板。
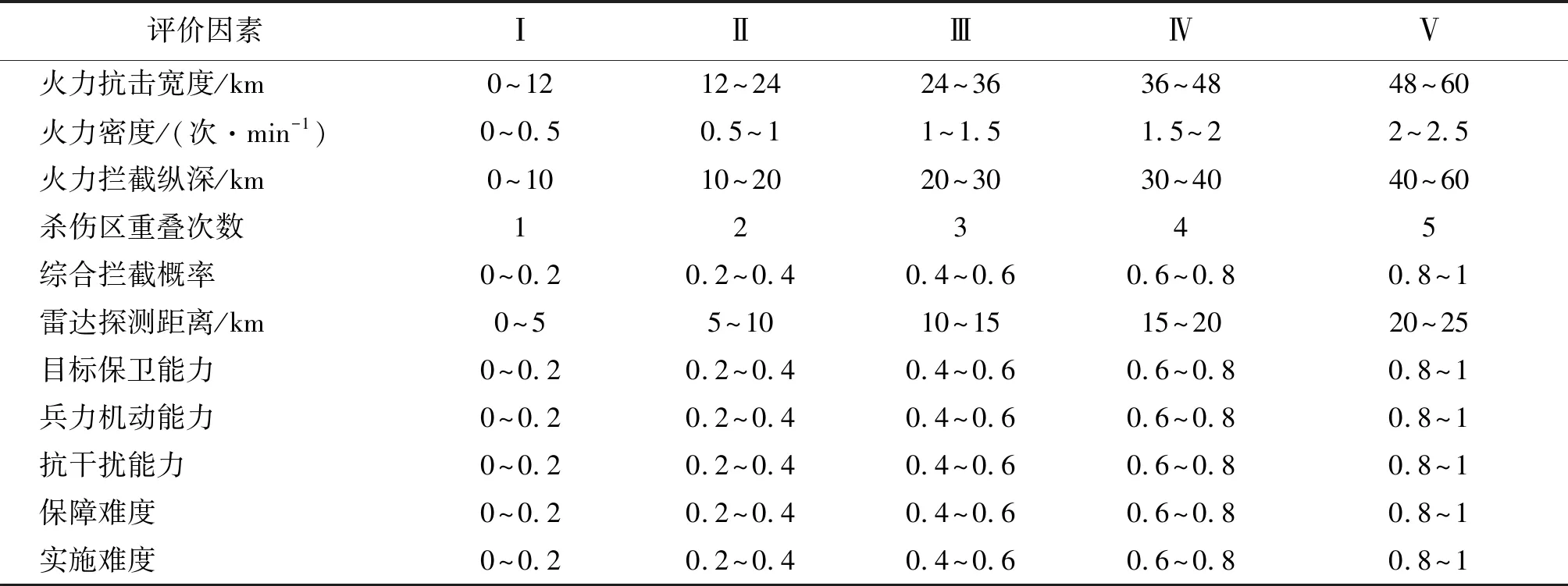
表6 部署因素分类评价标准Table 6 Classification and evaluation criteria of deployment factors

表7 评价等级赋分关系Table 7 Evaluation grade assignment relationship

表8 部署方案评判结果及优选排序Table 8 Evaluation results and optimization ranking of deployment schemes
4 结束语
本文提出基于相邻优属度熵权的模糊综合评判模型能够很好地解决地面防空部署评估及优选的过程中影响因素多,权重难以确定的问题。利用模糊综合评判自身的特点,和相邻优属度熵权确定权重的优点,避免了传统模糊综合评判方法、AHP法、专家调查法等主观性强或只考察一种不确定性的缺点,做到了主观判断与客观计算相结合,使部署方案评估优选更具有科学性。
