杀爆战斗部破片和冲击波对目标的耦合作用
2020-07-02侯俊亮蒋建伟李应波肖辉朗
侯俊亮 ,蒋建伟 ,李应波 ,刘 瀚 ,肖辉朗,肖 晗
(1.四川航天系统工程研究所,四川 成都 610100;2.北京理工大学 爆炸科学与技术国家重点实验室,北京 100081)
引 言
现有的杀爆战斗部目标毁伤理论一般是先将破片和冲击波对目标的作用单独考虑,再代数叠加作为最终综合毁伤结果[1-3]。这种基于单一毁伤元毁伤简单叠加方法,在一定程度上满足了战斗部设计和威力评价要求,但往往导致战斗部质量过大或威力半径过大等问题,在武器系统射击精度较低的条件下增加设计余量保证毁伤效果。然而随着武器射击精度的提高,对战斗部小型化和高效率提出强烈需求,研究人员需着力建立更精确的描述战斗部威力的理论模型。首先两种毁伤元一般不是同时作用于目标,其次一种毁伤元对目标的作用必然影响后次序毁伤元的作用效果,两者是耦合的而不是完全孤立的。
多年来国内外学者对冲击波和破片耦合作用下目标的动态响应问题进行了大量的研究,但由于机理复杂,不易建立准确的分析模型。往往采用试验方法,对特定条件下特定结构的耦合毁伤进行试探性研究。美国弹道研究试验室的Joshua E.等[1]提出破片、冲击波对飞机目标有耦合毁伤作用,并开展了相关的耦合毁伤试验。美国空军工程服务中心Marchand等[2]对平板目标在破片、冲击波单独作用下及耦合作用下的响应进行了试验研究。瑞典Chalmers工程大学的Ulrika等[3]利用AUTODYN对两端固支混凝土梁结构在破片与冲击波耦合作用下的动态响应问题进行了数值模拟,结果均表明破片冲击波具有耦合作用且远大于单独作用的简单叠加。研究并应用先进的战斗部毁伤元设计理论,是战斗部领域亟待解决的问题。
考虑到杀爆战斗部对付的许多军事目标如车辆、雷达等多为平板型结构,在目标易损性研究中,往往采用一定厚度的平板替代真实目标进行毁伤效应分析[4-5]。本研究选取平板作为典型目标,分析了破片先穿孔、冲击波再作用的情况下破片和冲击波的耦合作用并给出了量化计算方法,以期为破片杀伤战斗部的设计和威力评估提供参考。
1 模型及量纲分析
冲击波初始速度高、衰减快,破片初始速度相对较低但衰减慢。两种毁伤元对目标的作用一般有先后顺序,当战斗部距目标非常近时,冲击波先作用于目标,破片后作用,此时耦合作用不明显;当距离目标相对远时,破片先对目标作用,冲击波随后对有预损伤结构作用,为本研究耦合毁伤的研究范围。
物理模型如图1所示,一定质量的装药在周向约束的平板中心点上方H处起爆,在冲击波的作用下,平板凹陷产生塑性变形。中心点挠度是平板动态响应的重要参数,选取其作为评估冲击波对目标毁伤效果的参考指标。为了方便得到孔参数对多孔平板挠度的影响规律,对物理模型做如下假设:
(1)由于塑性变形过程非常短暂,忽略了热效应;
(2)常温下材料为应变率不敏感材料,忽略应变率效应;
(3)假设破片穿孔在平板上均匀分布;
(4)选取方形平板作为研究对象。

图1 物理模型示意图Fig.1 Diagram of the physical model
破片穿孔对平板的结构造成了预破坏,在冲击波载荷作用下结构更容易变形,强度的减弱情况与孔的形状、大小、密度及分布情况相关。以下将选取多孔平板在冲击波作用下的挠度Df相对于无孔平板挠度D0的增益作为破片冲击波耦合作用因子进行研究。
选定影响Df的独立物理量为:冲击波载荷冲量i+、材料弹性模量E、材料密度ρ、平板边长l,平板厚度h、孔直径df和无量纲参数孔密度nf,对其进行量纲分析,结果如下:
(1)
定义挠度增益系数Kf如下:

(2)
无孔和预制孔受到冲击波作用时,假设平板的强度削弱系数与冲击波载荷无关。孔的面积与平板相比小得多,孔对平板承受载荷冲量的影响可以忽略,而平板一般厚度尺寸远小于边长,代入式(2)后式(1)中第一项和第三项可认为是常数,式(2)可简化为:
(3)
可以看出,Kf只是平板厚度、材料性能、破片穿孔密度和穿孔直径的函数。
2 数值模拟及试验验证
2.1 数值模拟
根据量纲分析的结果,为了获得预制孔参数、平板材料及厚度对平板挠度的影响规律,结合物理模型确定计算模型如下:装药设计为1kg、截面长径比为1的圆柱形TNT,装药单点起爆不考虑爆轰产物对平板的作用。选择平板长宽尺寸为400mm×400mm,2mm厚Q235钢和4mm厚2A12铝板两种材料及无孔、4孔、9孔、16孔和25孔的预制孔方案,用AUTODYN软件对问题进行建模和求解,冲击波场采用Remap映射方式模拟以提高效率。数值模拟模型及参数见文献[6],计算模型如图2所示(图中为无孔平板1/4模型)。

图2 数值计算模型Fig.2 Simulation model
典型时刻Q235无孔靶板和16孔Φ8mm靶板应力云图见图3(考虑到对称性,为1/4模型)。
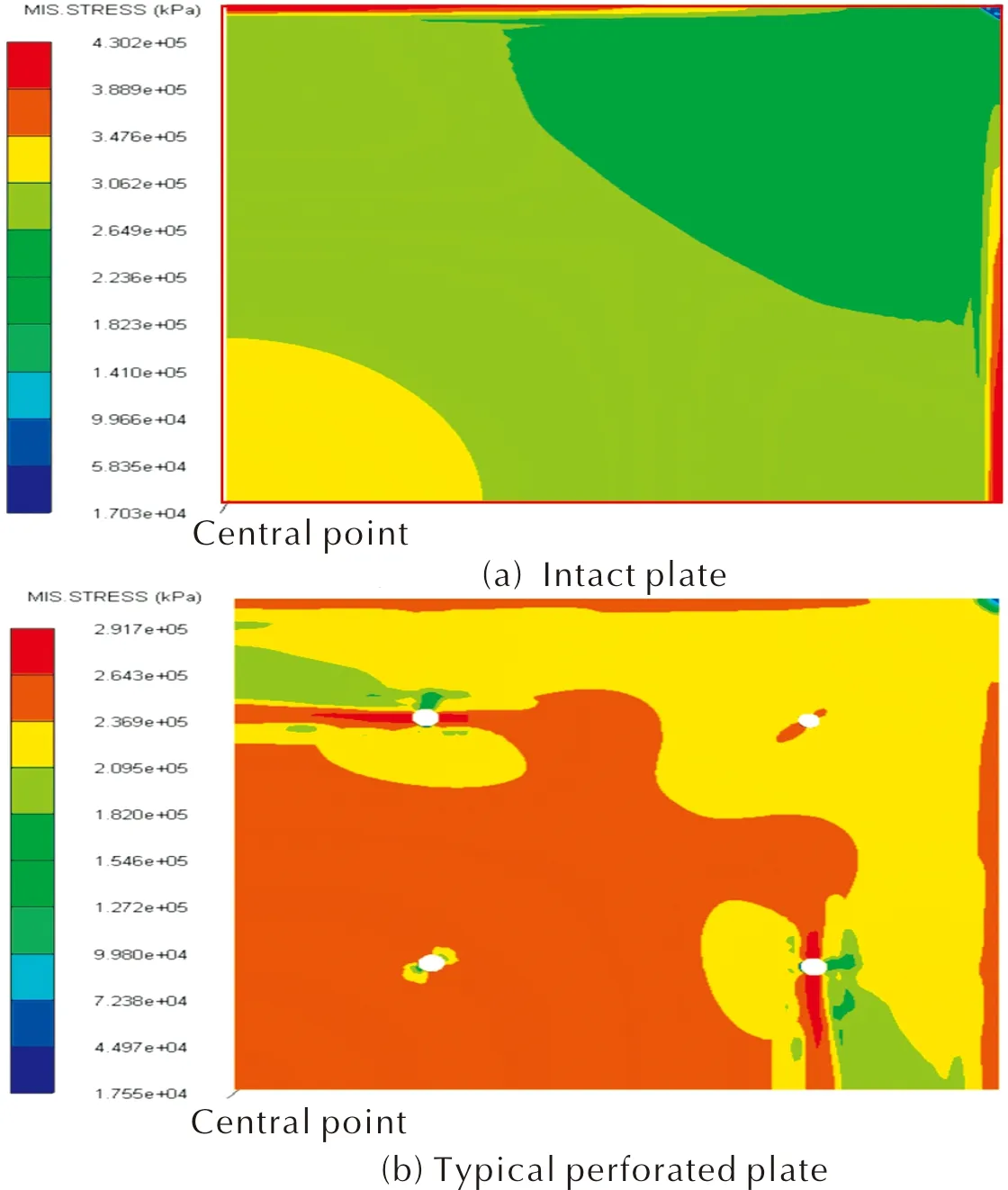
图3 典型时刻靶板应力状态Fig.3 Stress state of the target plate at typical time
从应力极值看,所有工况平板的应力极值均出现在约束边界处,无孔平板极值最高,随着预制孔密度的增加极值呈递减趋势,可见预制孔处冲击波能量的泄露对平板受到的冲击载荷大小有一定影响。
从应力区域分布看,预制孔的存在使得平板上应力分布复杂而凌乱,平板上也出现了很多高应力值区域,预制孔附近也有明显的应力集中,因此有孔平板最终体现出更大的挠度变形。
典型工况Q235靶板中心点挠度D数值计算结果见图4。

图4 典型工况Q235靶板中心点挠度模拟曲线Fig.4 Deflection simulation curves of Q235 target center point under typical working condition
从图4结果看,随着孔密度的增加,有孔平板的挠度明显增加。
2.2 试验验证
试验现场见图5。试验选择在开阔平整场地进行,与计算模型尺寸1∶1布置。靶板材料、厚度与数值模拟一致,靶板设无孔和预制孔两种,预制孔靶板孔数有均布4、9、16个孔3种,孔径分别为4、6和8mm。1kg TNT炸药位于靶板中心正上方,药柱底面距靶板中心点高度H为1m。

图5 试验现场布置[7]Fig.5 Layout of the test site
部分靶板试验结果见图6。钢和铝两种材质靶板周边可靠约束,在爆炸载荷作用下中心点出现较大挠度变形,现象与数值模拟一致。


图6 部分靶板试验结果Fig.6 Part of the plate experiment results
2.3 试验结果与数值模拟结果对比
试验与数值模拟结果见表1和表2。

表1 2A12铝靶板中心点挠度的试验值与模拟值对比
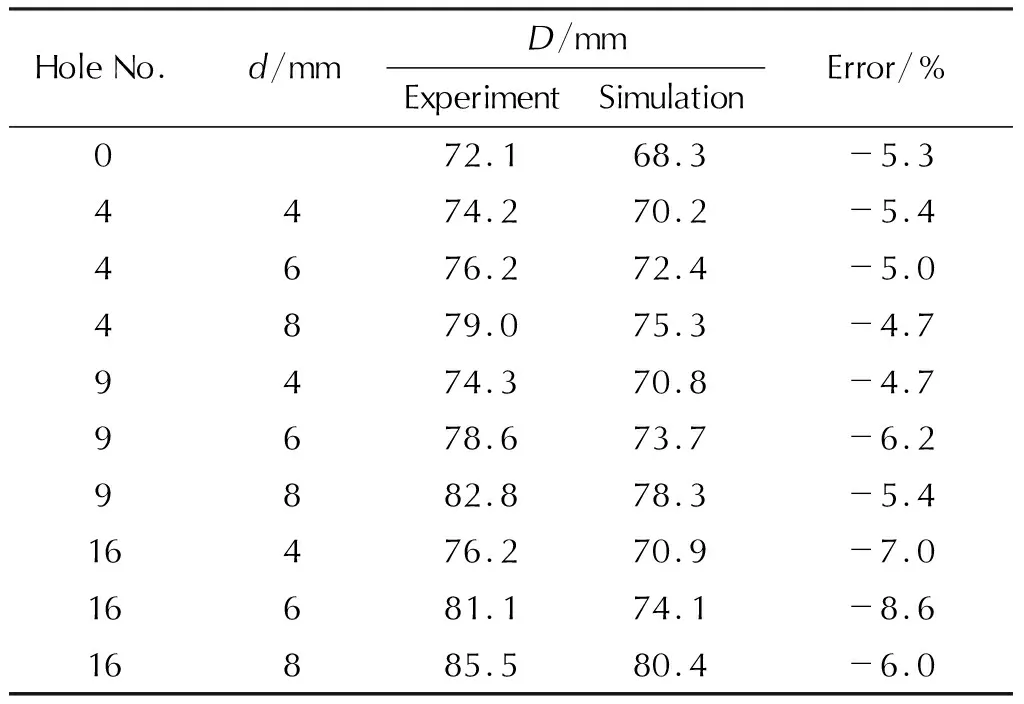
表2 Q235钢靶板中心点挠度的试验值与数值模拟值对比
由表1和表2可知,两种方法获得的结果有较好的一致性,在相同冲击波载荷作用下,两种材料的预制孔靶板表现为更大的挠度,随着孔密度和孔径的增大,预制孔靶板的挠度增益逐渐增大。
由于数值模拟中对靶板四边节点完全约束,而实验中采用有限个螺钉对靶板四边固定,实验后靶板螺钉约束处有明显的扩孔现象,受此影响中心点挠度值有所增加,试验结果与数值模拟方法相对误差(绝对值)均小于9%,数值模拟结果可信,可用于模型构建。
3 破片冲击波耦合作用模型
破片冲击波耦合作用是以有孔平板相对于无孔平板的挠度变形增量来表征。公式(2)和公式(3)给出了与无孔平板相比,预制孔平板在爆炸冲击波作用下中心点挠度增益系数。
首先根据公式(2)自变量取x1=σs/E×103,x2=nf,x3=df/h,采用共轭梯度法将Kf作三元函数拟合获得两种材料归一化模型:
Kf=f(x1,x2,x3)=
(4)
其中,Q={0 拟合获得参数:p0=-2.304×10-5,p1=67.83,p2=-5.15,p3=0.0135,t1=-0.944,t2=1.413,t3=0.618,b0=1.0221。 Kf的三元函数拟合曲线见图7。由图7可看出曲线存在零点非零、拟合误差太大及数据重叠等问题,无法用于工程计算。 图7 Kf的三元函数拟合曲线Fig.7 Fitting curves of the ternary function of Kf 分别对两种材料参数进行二元拟合,假设孔密度和孔径为独立变量,规定x1=nf,x2=df/h,分别给出Q235钢和2A12铝材料平板的Kf二元函数形式为: (5) 拟合Q235钢的Kf获得参数t1=1.953,t2=0.003,t3=-5.832×10-6,b1=0.472,b2=0.0196,b3=-0.00165。自变量取值范围0 拟合2A12铝板的Kf获得参数t1=0.217,t2=0.000281,t3=-7.905×10-7,b1=4.325,b2=0.165,b3=0.00907。自变量取值范围0 图8 Q235钢板及2A12铝板的Kf二元函数拟合曲线Fig.8 Fitting curves of the binary function of Kf Q235 and Kf 2A12 二元函数拟合获得的两公式的相对误差均在3.5%以内,拟合点的平均相对误差为1%~2%,精度可满足使用要求。 根据已建立的破片与冲击波耦合毁伤模型,采用C++编制了计算程序。以某型相控阵雷达为典型目标,对不同弹目交会条件下某型“百舌鸟”反辐射导弹战斗部对目标的毁伤情况进行计算。相控阵雷达天线阵面长2.4m、宽2.4m,共有5161个天线阵元。“百舌鸟”导弹战斗部为预制破片杀爆战斗部,质量66.7kg,主装药为Octol、装药量23kg,破片为边长4.8mm的钢立方体破片,总质量16kg[9]。冲击波载荷计算时对带壳装药战斗部进行了裸装药等效折算。 破片穿孔后造成天线面元结构预损伤,冲击波更容易对周边面元进行毁伤,破片冲击波有耦合作用,假定其与本研究提出的增益系数呈线性关系,可利用本研究成果进行算例对比。根据毁伤判定,当雷达毁伤面积达15%以上,即超过775个天线单元被毁伤时,雷达功能才会受到影响。破片对天线面元的毁伤按照交会后每个破片毁伤一个天线单元计算,冲击波对每个天线单元毁伤判定按照PI准则进行[9],遍历整个天线阵面便获得冲击波毁伤的百分比。 分别定义破片、冲击波耦合毁伤模型及独立毁伤模型计算得到战斗部的杀伤半径为rc和ri。利用计算程序对给定的不同破片着角及破片穿孔密度条件进行计算,得到破片冲击波耦合毁伤及独立毁伤简单叠加模型下的战斗部杀伤半径曲线,为了便于对比,数据处理时对破片穿孔密度nf取自然对数,计算结果如图9所示。 图9 不同工况下不同毁伤模型毁伤半径计算结果Fig.9 Calculation results of the damage radius under different damage models and different working conditions 由图9可见,将破片和冲击波毁伤效应独立处理时,战斗部的毁伤半径ri随着破片穿孔密度的增加变化不明显,而考虑了破片穿孔造成结构弱化的耦合毁伤模型获得的杀伤半径rc则随着破片穿孔密度nf的增加逐渐提高,且nf越高rc提高的幅度越明显,算例中杀伤半径最大提高幅度9.5%。破片与雷达面的不同着角对应不同的穿孔直径,随着角的增大,穿孔直径呈增大趋势,因此耦合毁伤半径随着角的增大也呈增大趋势。 当穿孔密度较低时,耦合毁伤效果并不明显,模型计算获得的杀伤半径值与独立毁伤模型计算基本相同,随着破片穿孔密度的增加,耦合毁伤模型计算的杀伤半径逐渐远大于独立模型杀伤半径。可见,在一定范围内控制弹目交会条件,在目标形成一定的穿孔,由于破片与冲击波的耦合作用,能有效提高毁伤效果。 综上,耦合毁伤模型与单独毁伤模型相比,其特点是考虑了破片先作用后结构的预损伤,将冲击波与破片耦合作用量化。应用耦合毁伤模型对杀爆战斗部的毁伤半径评估时,当装药量不变时,评估得到的杀伤半径有所提高;当规定杀伤半径不变时,毁伤目标所需的装药量减少。这对战斗部的精确化和小型化设计具有一定的现实意义。 (1)根据破片对平板先穿孔、冲击波后作用的特点,提出了冲击波作用下以有孔平板相对于无孔板的挠度增益表征破片与冲击波耦合作用的毁伤评价模型。 (2)利用试验验证过的数值模拟结果数据,采用共轭梯度法对模型参数进行了拟合获取,拟合误差低于3.5%。 (3)应用建立的耦合毁伤模型对典型目标进行了毁伤计算,结果显示相同工况下,耦合毁伤评估获得的杀伤半径较独立毁伤叠加模型有所提高,最大幅度达9.5%。 (4)提出的模型可作为杀爆战斗部对典型目标的耦合毁伤量化评估方法,可为破片杀伤战斗部对典型目标的工程设计和威力评估提供一定的参考。

4 应用算例

5 结 论
