Explosion Test and Power Evaluation on Non-ideal Explosives

XU Qi-peng , ZHANG Yu-lei, LI Zhi-rong, SU Jian-jun ,LIU Yan,HUANG Feng-lei

(1.State Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology, Beijing 100081, China; 2.Xi′an Modern Chemistry Research Institute, Xi′an 710065, China)

Abstract:The explosion experiments of cyclotetramethylene tetranitramine (HMX) based aluminized explosive (AE) were carried out in free filed. The shock wave parameters and heat effect data were obtained through theoretical calculation and instrument acquisition. Based on the explosion effects, a method for evaluating the power of AE was proposed. Results show that, in the experimental range, the overpressure (Δp) and impulse (I) of AE increase by 33.1% and 28.9% respectively compared with those of TNT in the largest position. The explosion fireball temperature and dimension are also much higher and greater, in high temperature range(greater than 2000℃), and the duration of AE is 7 times that of TNT. The method for evaluating the power of AE is more accurate to express its comprehensive power and helpful to compare the power of other similar non-ideal explosives.

Keywords:explosion mechanics; aluminized explosive; non-ideal explosive; shock wave; heat effect; power evaluation

Introduction

Aluminized explosives(AEs) as typical non-ideal explosives have attracted a lot of interest over the years since they are highly destructive in confined or semi-confined spaces such as field fortifications, weapons and ammunition warehouse, tunnels, ship cabin, and aeroshed[1-4]. Compared it with conventional high-explosive powder, instead of armor or fragmentation penetrating, its damage effects focus more on high heat and pressure[5-8].

The study on topic of AE could be categorized into two types, formulation and blast power. In AE formulations[9], a large proportion of Al fuels are usually used to generate the heat in a post combustion process after the detonation of the main charge. Due to its high ignition temperature or partial sluggishness during detonation, the optimum amount of Al might differ, depending on the type and content of the explosive fillers. One such example is the use of micrometer-sized Al that may agglomerate, resulting in lower combustion efficiency[10]. The use of nano-sized Al may improve the combustion performance and reduce the particle size of the final agglomerated products[11]. In order to improve the heat releases and combustion efficiency of Al in AE, many strategies have been developed. Such as, energetic blends of Al particles with liquid perfluoropolyethers oxidizers were prepared[12]. In this way, the reactivity of Al particle is improved, leading to a significant increase in the heat speed. In addition to fluoropolymer, the activation of Al could also be achieved by combining with the other metals. For instance, the equiatomic Al-Ni mixtures after milling can reduce exothermic onset by as much as 300℃[13].

On aspect of blast power, the shock wave and fireball data attracted full attention.Danica[14-15]initiated her study with the effect of different binders and oxidants on the shockwave parameters of AE through experiments. And then the effect of different size and quality of charge was studied as well. Maiz[16-17]devoted himself to studying the effect of different formulations of AE on the fireball temperature and shock wave data in finite space. Trzcinski[18-19]conducted varied experiments under different atmospheres to discuss the degree of afterburning effect and variety of quasi-static pressure of AE with coarse aluminium oxide or lithium fluoride particles. Later, the shock wave and quasi-static pressure effect of AE with diverse particle size in an open space and steel chambers were also considered. Our group once used detonation heat to calculate the peak air pressure of AE in free field, but the calculated value was 48% higher than the experimental data[20]. This is because detonation heat characterizes the heat released by explosive, the generative heat especially the secondary combustion of AE does not form the blast wave. In general, at present, researchers are mainly concerned about the formulation of AE and the influence of composition variety on blast performance, including heat, quasi-static pressure, and blast wave effects. However, there is no unified criterion to evaluate the power of AE. In this paper, we carried out blast experiments using aluminized HMX-based explosive, and obtained the shock wave and heat effect data. The blast performance was analyzed, and a method to evaluate the power of AE was proposed, which could also be applied to other non-ideal explosives.

1 Experiment

1.1 Sample characteristic and instrumentations

The charges are 5kg cylindrical AE, which were composed of three pellets of HMX/Al /binder (mass ratio of 58∶32∶10) composition. The pellets had a density of 1.86g/cm3and were glued together. The thickness of Al has two sizes of 20 μm and 2μm.

The PCB 211B series pressure transducers buried underground were used to record the reflection pressure time history. Data acquisition instrument Genesis 986A05151, was used to deal with the captured signal. Infrared thermometer SC3000 (50Hz sampling frequency and 1.1mrad spatial resolution) and high speed camera Phantom V7.3 were used to observe the temperature and size of the fireball.

1.2 Experimental method

In the test, the charges were placed vertically on a trestle in the air 1.5m above the ground. The booster used was JH-14, and the initiating agent was 8# detonator. Two lines of pressure transducers with an angle of 60° were distributed around the blast center. Each line had nine measuring points designated as No.1-9 to monitor the shock wave pressure-time history. The stand-off distance of two lines from the measuring points to the explosion center are 2.73,3.62, 4.54, 5.5, 6.36, 7.3, 9.1, 11.0 and 12.8m, respectively. The high speed camera and infrared thermometer were placed 100 meters away from the explosion center, to record fireball evolutions and its surface temperature. Fig.1 shows the layout between experimental device and explosion center.

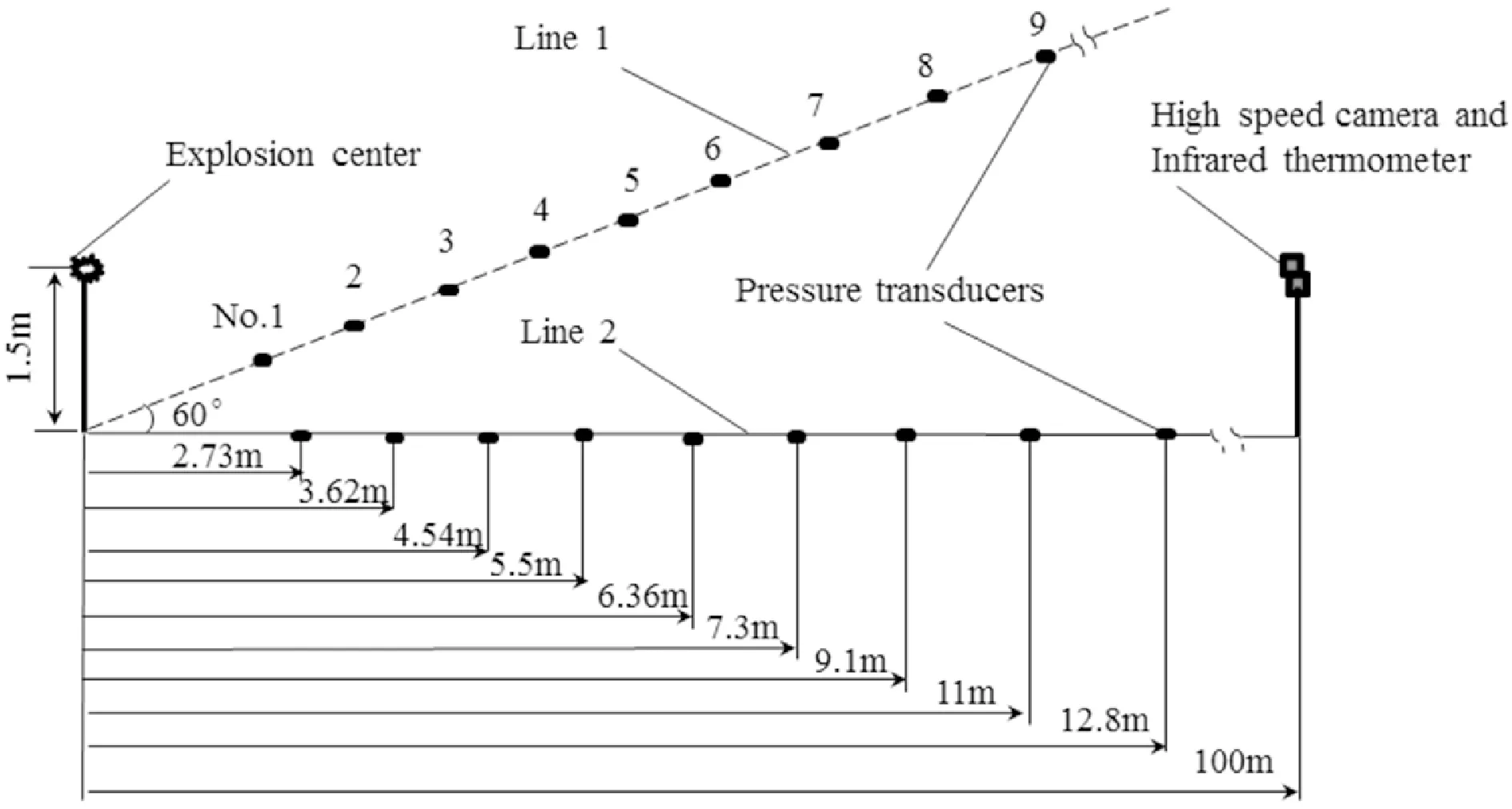
Fig.1 Diagram of layout between experimental device and explosion center

2 Results and discussions

2.1 Shock wave parameters

The pressure transducers measure the voltage valueΔU, which is converted into the peak air pressureΔpby Eq.(1), and then calculates the impulseIwith Eq.(2). Values ofΔpandIdetermined on the basis of two pressure histories are summarized in Table 1. Fig.2 shows the blast wave pressure-time curves of TNT at stand-off distance of 3.62m and 6.36m on two contrast lines. It can be seen that the arrival times of the blast wave peak pressure at the same distance are basically the same, and the peak pressures are in slightly different, which may be caused by the flatness of the ground in the experimental site.

(1)

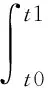
(2)

Wheresis the transducer sensitivity;t0andt1are start time and end time of positive pressure, respectively;Δpis the peak air pressure.

From Table 1, we see that the peak pressure and impulse of AE at different stand-off distances are both significantly higher than those of TNT. The peak pressureΔpand impulseIimproved by 33.1% and 28.9% at No.1 position (2.73m), respectively. The results of experimental overpressure and impulse data in Table 1 are shown in Figs.3 (a) and (b). As shown, the fitted curves in each figure have the similar trends. The overpressureΔpand impulseIof AE are always higher than those of TNT in the near field, however, the gap is very small in the far field. This is because the shock wave is a spherical wave, which is gradually clouded and rapidly attenuated during propagation.

Fig.2 The shock wave pressure-time curves at stand-off distance of 2.73m and 5.5m on two contrast lines

Table 1 Values of Δp and I obtained from the overpressure histories

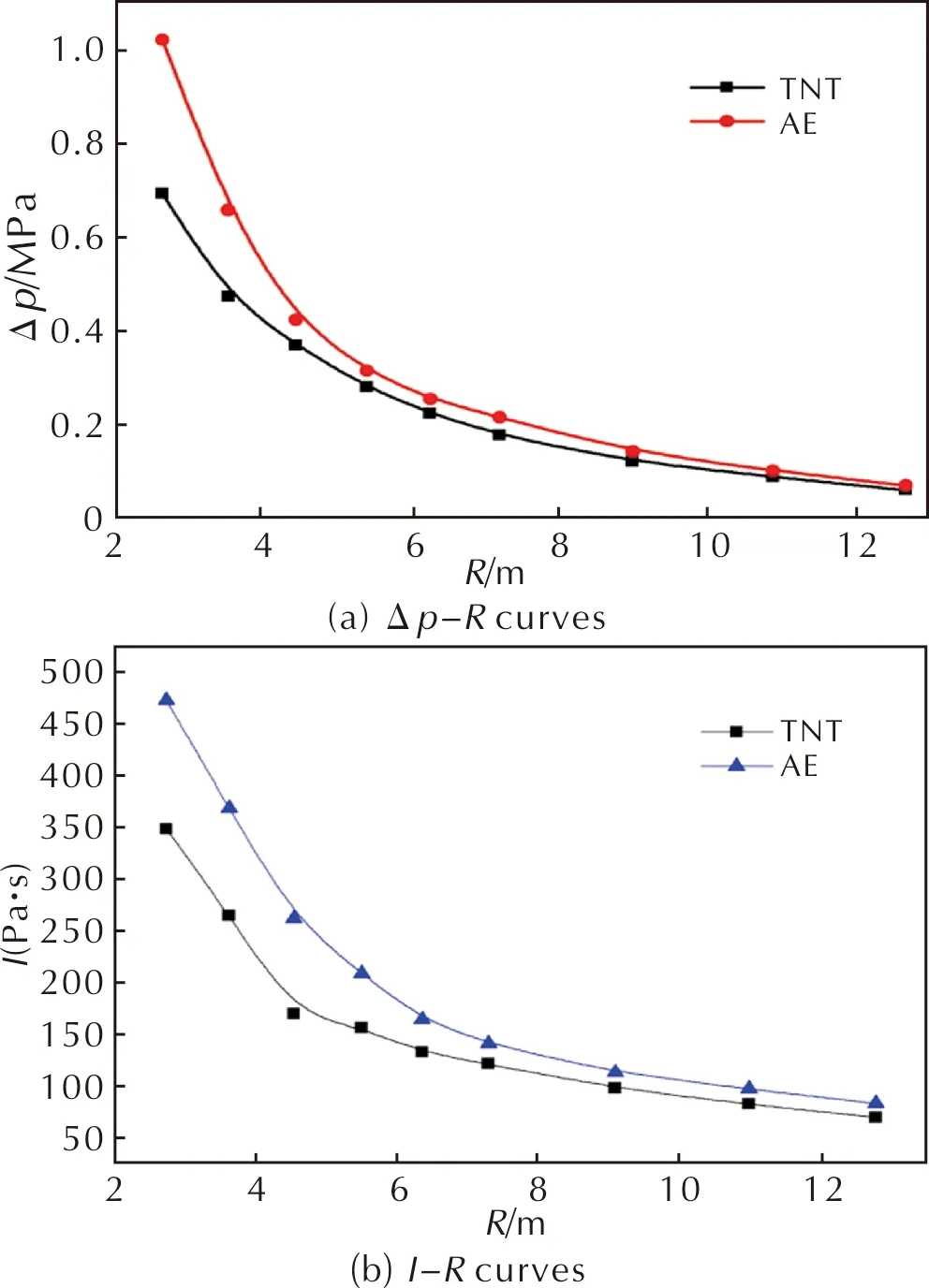
Fig.3 The fitted curves of shock wave data along the stand-off distance

2.2 Heat effect parameters

For most objects, heat effect may change properties of the targets as theirs internal temperature rise, even creep orbuckling[21-22]. Obtaining the heat effect data is of great importance to study the power of AE. The infrared thermometer was used to measure the surface brightness of the fireball, and its surface temperature could be evaluated by means of the following expression[23].

L=ε(T)T4σ/π

(3)

WhereLstands for the brightness of the object;ε(T) means the total emissivity of the object, generally is among 0.3-0.45, which was taken 0.35 here[23-24]; Stephen boltzmann's constant 5.67×10-8W/(m2·K4).Trefers to the absolute temperature of the object.

Temperature higher than 1000℃ were plotted in Fig.4.

Fig.4 The fitted curves of temperature histories

From Fig.4 we can see that duration is 320ms for AE, but 260ms for TNT. When temperature higher than 2000 ℃, the duration is 140ms for AE, but only 20ms for TNT, the former value is 7 times that of the latter, AE are more effective at high temperatures. Besides, after the temperature reaches its maximum value, it begins to decay, but the attenuation curve of AE is slower than that of the examined TNT charge due to the combustion of Al particles included only in AE. The set of images captured by the high speed camera are presented in Fig.5. The image analysis was employed to quantify the fireball size, as well as its characteristic features with time. It could be seen that the fireball shape of AE is flatter than TNT, and AE owning a larger fireball volume at the same moment. Both fireball temperatures of the two explosives have the feature of high center temperature and low surrounding temperature, even though there are also differences, the TNT fireball temperature decays monotonously from the center to the periphery, and there are several high temperature zones scattered in AE explosive fireball. After 100ms, under the action of ground reflected pressure and rarefaction wave, the fireball begins to gradually exhibit ineffectiveness. When the fireball temperature decay to 1000℃, the size of the fireball of AE attained its maximum diameter 4.8m , and TNT is only 4m, the former is 1.2 times the latter.

Fig.5 Flame propagation after explosion of TNT and AE in the open field before 100ms by a high speed camera

2.3 Power evaluation of the AE

Through experiments presented in the previous section and analysis, one can observe that the main destructive effects of AE in the free field are shock wave and heat effect[15-16,18]. When assessing the power of AEs, it is inaccurate to take blast pressure or detonation heat as the object of comparison. As we had confirmed when assessing the power of AE only with detonation heat, the calculated overpressure data was 48% higher than the experimental data[20]. On the other hand, a large proportion of Al power included in AE are used to generate the heat, the explosion characteristics of AE cannot be fully manifested only by the comparison of overpressure.

Theblast wave effects are not only related to the magnitude of peak air pressure, but also to the impulse.p-Idamage criterion is applicable to most of the impacted targets. So, the shock wave power of non-ideal explosive (Eq.(4) ) is expressed as a function of the overpressure and impulse.

Heat effects are mainly reflected in diameter, duration and surface temperature of the fireball. If we agreed the diameter and duration data of the fireball are those of the surface temperature higher than a certain value(take 1000℃ here), the parameters of the heat effects could be reduced to two reference values (diameter and duration). The power of the heat effects of AE can be expressed by Eq.5.

qshock=α1qΔp+α2qI

(4)

qheat=β1qD+β2qt

(5)

whereqΔp，qI，qDandqtstand for TNT equivalent of overpressure, impulse, fireball diameter and fireball duration, respectively.qshockandqheatrefer to TNT equivalentof shock wave and heat effect, respectively.α1,α2,β1,β2are weight coefficients.

According tothe dimensional analysis[25], the shock wave overpressure and impulse of TNT can be described as Eqs.(6) and (7), the diameter and duration of the fireball can be fitted by using the following Eqs.(8) and (9)[26].

(6)

(7)

D=d·m0.32

(8)

t=f·m0.32

(9)

Wheremandrrefers to the quality of TNT and the distance from the measuring points to the blast center, kg and m;Dandtstand for the diameter and duration of the fireball, m and s;a,b,c,A,d,fare correction factors.

The shock wave data and fireball data of TNT obtained from the experiments were substituted into Eqs. (6)-(9) respectively. The coefficients contained in the Eqs. were determined by fitting with the software of Matlab, and the results are as follows:

(10)

(11)

D=2.255×m0.32

(12)

t=0.147×m0.32

(13)

The overpressure and impulse data of AE obtained from the experiment were put into Eqs. (10) and (11), respectively, the value ofminverse solved were then divided by the quality of AE, the corresponding TNT equivalents of shock wave overpressure and impulse of AE at different measuring points were gained. And then, with Eqs. (14) and (15), the averaging TNT equivalent of overpressure and impulse were solved, the results are1.38 and 1.37 respectively. Bring the maximum fireball diameter of AE into Eq. (12), the TNT equivalentqDconverted from the maximum diameter of the fireball was obtained 1.76. The fireball duration of AE was substituted into Eq. (13), and the TNT equivalentqtembodied the fireball duration equals to 1.88.

(14)

(15)

whereqΔPiandqIjstand for TNT equivalent of overpressure and impulse at different gauge points.nrefers to the total gauge numbers, here, it equals to 9.

The comprehensive explosion power of AE should be the weighted average of TNT equivalent of shock wave effect and heat effect, described as Eq. (16).

qTNT=ε1qshock+ε2qheat

(16)

WhereqTNTstands for the power of AE;ε1,ε2are weight coefficients.

When we use Eqs.(4)-(16) to evaluate the blast power of AE, considering the damage effects are attributes of AE itself, ignoring the diversity of damage modes sensitiveness to different targets, the shock wave overpressure, impulse, diameter and duration of fireball are on equal footing. So, we takeα1,α2,β1,β2,ε1,ε2all equal to 0.5. By calculating with the above Eqs., we finally get the explosive power of this kind AE is 1.56 times TNT.

3 Conclusions

(1) The detonation experiments performed in free field showed that the strong thermobaric effects (blast wave and heat effects) could be generated by aluminized explosive. In the experimental range, compared with TNT, the overpressureΔpand impulseIof AE increased by 33.1% and 28.9% in the largest position respectively. The explosion fireball temperature and dimension are also much higher and greater. In high temperature range(greater than 1000℃), the fireball duration and size of AE are 1.23 and 1.2 times that of TNT successively.

(2)As the intense secondary combustion after detonation of AE, it is inaccurate to evaluate the power of AE only considering blast pressure or detonation heat. A calculating model described as a weighted average of TNT equivalent of shock wave effect and heat effect for evaluating the power of AE is proposed, which is better to revealing the explosion characteristics of AE. Considering the shock wave overpressure, impulse, fireball diameter and duration as a attribute of explosive itself, the weight coefficients are simplified to a specific value. And finally we get the explosive power of AE tested is 1.56 times TNT. The model provides a method for comparing the power of AE and other similar non-ideal explosives.