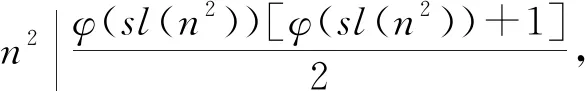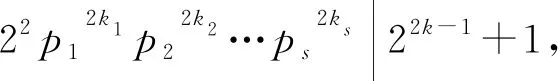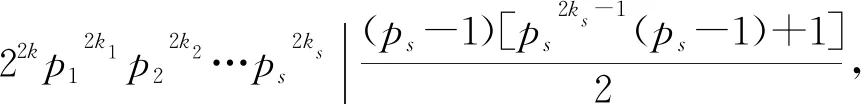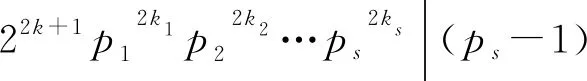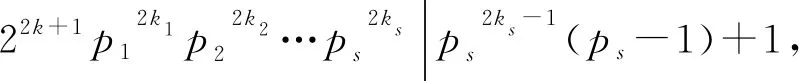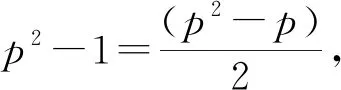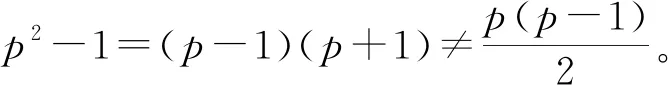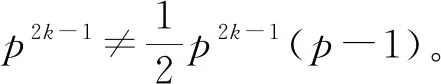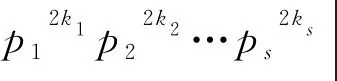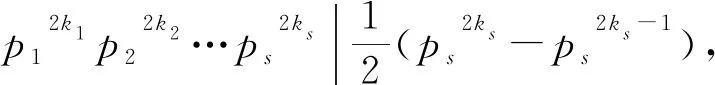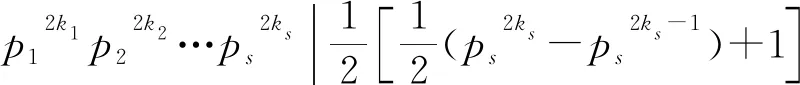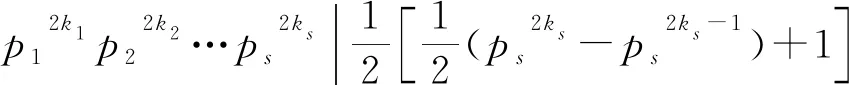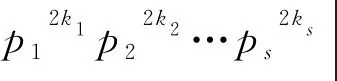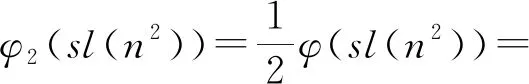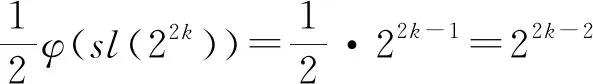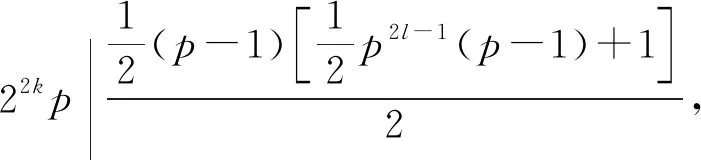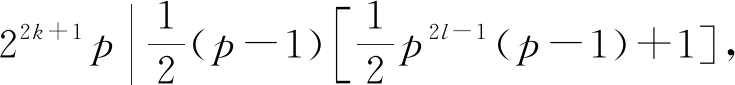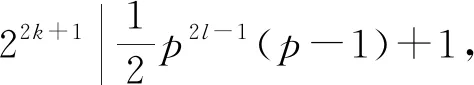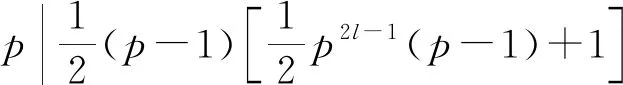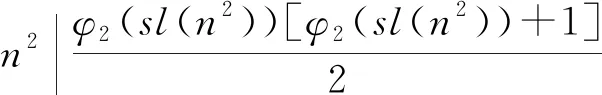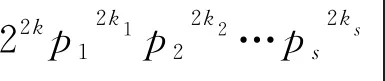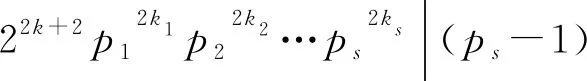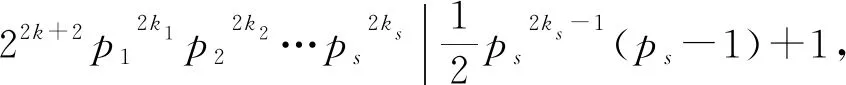包含Smarandache LCM函数的两个方程的正整数解

高 倩，高 丽，梁晓艳

(延安大学 数学与计算机科学学院，陕西 延安 716000)

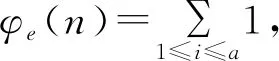
本文基于上述文献并在此启发下，讨论了数论函数方程z(n2)=φe(sl(n2)),(e=1,2)的可解性，并给出其所有的正整数解，结论丰富了有关函数的研究内容。

1 基本定义及相关引理

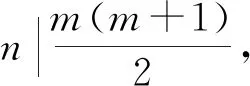
定义2[10]对任意正整数n，有

sl(n)=max{piαi}(1≤i≤k)，

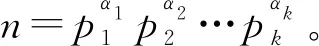
引理1[11]Euler函数为积性函数，即对于任意互素的正整数m，n，有φ(mn)=φ(m)φ(n)。

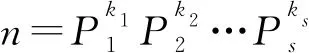
引理3[11]对于素数p与k≥1，则有

φ(pk)=pk-pk-1。

引理4[11]对任意素数p≥3,z(p)=p-1。

引理5[11]对任意素数p≥3及k∈N，z(pk)=pk-1。当p=2时，则有z(2k)=2k+1-1。

引理6[11]z(n)是不可加的，即

z(m+n)≠z(m)+z(n)；

z(n)也不是可乘的，即z(mn)≠z(m)z(n)。

2 主要结论及证明

定理1 方程z(n2)=φ(sl(n2))仅有正整数解n=1。

证明利用初等的方法给出定理的证明。

对于正整数n进行分类讨论。

(I)当n为奇数时，我们分以下几种情况进行讨论：

(i)n=1,z(12)=1=φ(sl((12))，所以n=1是方程的解。

(ii)n=p，其中p为素数，且p≥3，由于z(p2)=p2-1，而φ(sl(p2))=p2-p。

要使z(p2)=φ(sl(p2))，即p2-1=p2-p，显然p2-1=(p+1)(p-1)≠p(p-1)。

所以n=p不是方程的解。

(iii)n=pk，其中p为素数，且k>1,

z(p2k)=p2k-1，φ(sl(p2k))=p2k-p2k-1。

显然p2k-1≠p2k-1(p-1)。

所以n=pk不是方程的解。

φ(sl(n2))=φ(ps2ks)=ps2ks)-ps2ks-1。

若z(n2)=φ(sl(n2))，则由z(n)的定义可得

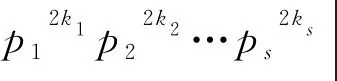
(1)

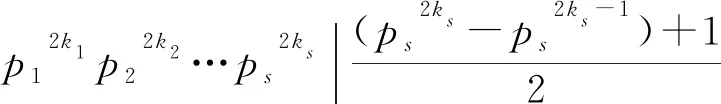
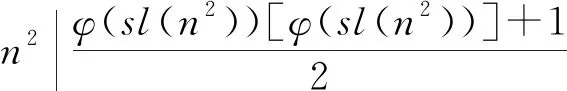
所以n=p1k1p2k2…psks不是方程的解。

(II)当n为偶数时

(i)n=2k其中k>0，显然z(2k)=2k-1为奇数，而φ(sl(n2))=φ(sl(22k))=22k-1为偶数，所以n=2k不是方程的解。

(ii)n=2kpl其中k>0，p为奇素数，l≥1。

(a)当sl(22kp2l)=22k时，

φ(sl(22kp2l))=φ(22k)=22k-1。

若z(n2)=φ(sl(n2))，则由z(n)的定义可得

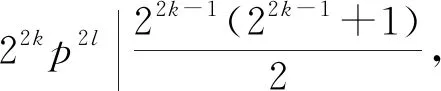
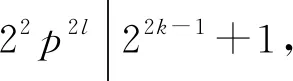
(b)当sl(22kp2l)=p2l时，

φ(sl(22kp2l))=φ(p2l)=p2l-1(p-1)，

若z(n2)=φ(sl(n2))，则由z(n)的定义可得

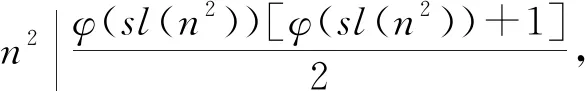
而(22k,p)=1，

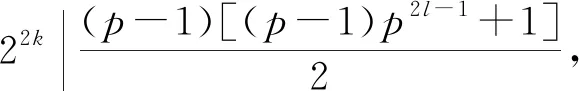
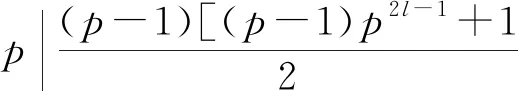
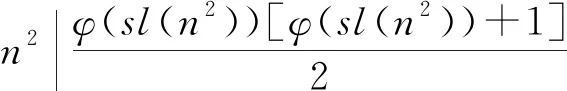
所以结合(a)(b)，此种情况不是方程的解。

(iii)当n=2kp1k1p2k2…psks其中p1,p2，…ps，均为大于2的奇素数，且p1k1

(a)当sl(22kp12k1p22k2…ps2ks)=22k时，

φ(sl(22kp12k1p22k2…ps2ks))=φ(sl(22k))=

φ(22k)=22k-22k-1=22k-1。

若z(n2)=φ(sl(n2))，则由z(n)的定义可得

(b)当sl(n2)=max{pi2ki}，(1≤i≤s)时记sl(n2)为ps2ks。

此时φ(sl(n2))=φ(ps2ks)=ps2ks-1(ps-1)。

若z(n2)=φ(sl(n2))，则由z(n)的定义可得

结合(a)(b)得n=2kp1k1p2k2…psks不是方程的解。

综上所述，方程z(n2)=φ(sl(n2))只有n=1这一个正整数解。

定理2 方程z(n2)=φ2(sl(n2))无正整数解。

证明(Ⅰ)当n为奇数时，

(i)n=1，z(12)=1,φ2(sl(12))=0，0≠1，所以n=1不是方程的解。

(ii)n=p，其中p为素数，且p≥3，由于

z(p2)=p2-1,

所以n=p不是方程的解。

(iii)n=pk，其中p为素数且k>1,

z(p2k)=p2k-1，

所以n=pk不是方程的解。

(iiii)n=p1k1p2k2…psks，其中p1，p2，…ps，均为大于2的奇素数，且p1k1

若z(n2)=φ2(sl(n2))，则由z(n)的定义可得

不成立。

即n=p1k1p2k2…psks不是方程的解。

(Ⅱ)当n为偶数时，

所以n=2k不是方程的解。

(ii)n=2kpl，其中k>0，p为奇素数，l≥1。

(a)当sl(22kp2l)=22k时，

若z(n2)=φ2(sl(n2))，则由z(n)的定义可得

亦即23p2l|22k-2+1，显然不成立。

所以n=2kpl不是方程的解。

(b)当sl(22kp2l)=p2l时，

若z(n2)=φ2(sl(n2))，则由z(n)的定义可得

结合(a)(b)两种情况，n=2kpl不是方程的解。

(iii)当n=2kp1k1p2k2…psks，其中p1,p2，…ps，均为大于2的奇素数，且p1k1

(a)当sl(22kp12k1p22k2…ps2ks)=22k时，

φ2(sl(22kp12k1p22k2…ps2ks))=

若z(n2)=φ2(sl(n2))，则由z(n)的定义可得

即22kp12k1p22k2…ps2ks|22k-3(22k-2+1)，

即23p12k1p22k2…ps2ks|22k-2+1，显然不成立。

所以此种情况不是方程的解。

(b)当sl(n2)=max{pi2ki}，(1≤i≤s)时记sl(n2)为ps2ks。此时

若z(n2)=φ2(sl(n2))，则由z(n)的定义可得

所以此种情况不是方程的解。

结合(a)(b)两种情况，n=2kp1k1p2k2…psks不是方程的解。

综上所述，该方程无正整数解。