水平管气液段塞流流动特征模拟

吴 晓，王兆婷，史 瑶

（1.中国石油大学胜利学院，山东东营257061；2.中国石油大学（华东）储运与建筑工程学院，山东青岛266580；3.中国石油新疆油田分公司工程技术研究院，新疆克拉玛依834000）

水平管气液两相段塞流广泛存在于石油、化工和核能等领域。段塞流流动带来的压力和流量波动对一些生产设备的设计具有重要影响，所以深入研究水平管段塞流的流动特性具有重要的学术意义和应用价值。由于段塞流流动的复杂性，对其流动特性的研究多采用实验平均测量的手段，其只能给出宏观规律特征，而CFD更能细致地捕捉到瞬态流动特征、起塞机理及气液段塞流相界面结构特征，选取准确的模型能够保障多相流管道的安全设计和操作。

目前已有的气液段塞流的计算模型可以分为稳态模型和瞬态模型两类。段塞流的稳态模型使用较为广泛但存在一些缺陷，使用段塞流稳态模型前需要进行流型判断，段塞流稳态模型只能给出段塞流的平均特征参数；同时Y.Taitel等[1]研究表明，稳态模型在计算下倾管段塞流时常出现非物理解。

段塞流瞬态模型大致可以分为一维双流体模型、液塞跟踪模型和界面捕捉模型。一维双流体模型一般都基于M.Ishii[2]推导的一维双流体模型框架基础上建立的。但针对不同流型建立的守恒方程和方程的本构关系却有很大的差异。M.Lu[3]通过实验和模拟相结合方法对水平管段塞流的起塞、成长及合并的过程进行研究，并对六种CFD软件进行对比分析，发现TRIOMPH下的一维双流体模型对段塞流瞬态特征的模拟存在以下问题：只能捕捉由K‐H模型不稳定产生的长波，不能考虑到界面扰动带来的短波影响。一维双流体模型具有较好的适用性，但存在很多缺点：计算范围具有局限性，超出范围出现数值发散、病态无解情况；界面阻力的本构方程不够成熟；能够预测管道内压力波动特征，对液塞演化过程的预测不理想；一维模型不能模拟入口几何条件，无法模拟入口扰动带来的影响及三维下的液塞演化过程。

G.Zheng等[4]较早提出了液塞跟踪模型，该模型是通过对每个液塞头尾位置的Lagrangian追踪，模拟液塞的运动、成长和消失的演化过程，能够较好地模拟段塞流的瞬态特征。但液塞跟踪模型存在如下缺陷：计算时必须在入口处给定液塞长度分布，不能从根本上模拟追踪液塞的自然演化过程；模型中气弹移动速度与前方液塞长度的关系式是基于低气液速度的实验得到的，对于高气液速的工况计算有待验证。

最近发展起来的界面捕捉模型具有如下优点：不同流型可采用相同的控制方程和本构关系式；通过数值求解自动捕捉液塞的自然演化过程，不需引入额外扰动；能够真实地反映出起塞机理、段塞流的瞬态流动特性及相界面结构特征。

目前段塞流模拟多数依靠一维、二维模型，不能很好地反映实际情况下相界面结构和瞬态流动特征，M.Lu[3]、S.C.K.De Schepper[5]、M.Abdulkadir[6]等通过 Ansys、Fluent、STAR‐CD 等商业软件建立三维模型对段塞流进行模拟，结果并不理想。作为开源软件，OpenFoam拥有强大的底层类库，充分利用了C++封装、继承、多态等特点，减小二次开发难度，用户可以自由的对算法、边界条件、求解器等进行研究开发，根据模拟情况选择最适合自己的模型，为CFD领域的研究者们提供了一个强大的开源平台。

综上所述，本文基于OpenFoam[7]开源软件，利用界面捕捉方法建立统一的两相流流动三维数值模型，无需外加扰动，对段塞流的自然起塞机理和液塞的成长、演化过程进行深入细致的研究，并与理论、实验相比较验证模型的有效性。

1 两相流数值模型

基于三维两相流数值模拟的复杂性，对其进行假设：气、液相为不可压缩流体；两相之间无传热和传质现象；气、液相与管壁之间为无滑移边界条件。

1.1 VOF模型

VOF模型最早由C.V.Hirt等[8]提出，之后由E.Berberovi'c等[9]针对两相流进行改进，通过求解单独的动量方程和关于流体体积函数的微分方程，间接实现单元体的界面追踪，基本原理如图1所示。

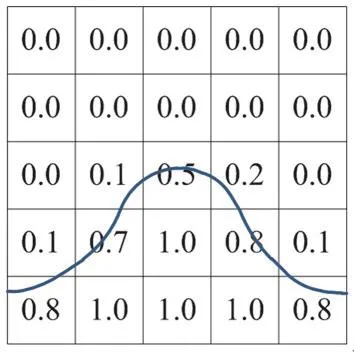
图1 VOF界面追踪原理Fig.1 Schematic diagram of VOF interface tracking

函数α守恒方程为：

体积分数守恒对于流动来说非常重要，微小的体积分数误差都会导致界面位置的较大变化，为了减少气液相界面之间的模糊边界，对α的传输方程加入人工压缩项，改进后方程为：

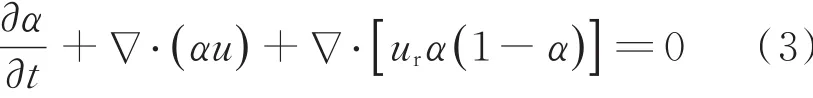
式中，u为瞬时速度，ur为压缩界面的速度场，即气、液相的相对速度，限制了α的求解区间为0～1，即人工压缩项仅对相界面有作用，对气液相内部不产生影响。局部流体物理性质，如ρ、μ通过体积分数对两种流体加权得到。

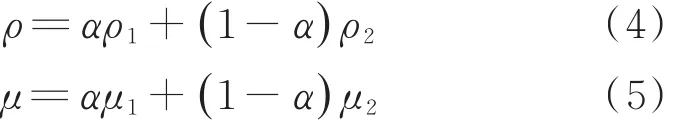
1.2 控制方程

模型采用单流体法，气、液共用一套质量、动量方程，与体积分数传输方程组成封闭方程，控制方程为：

式中：P为压强；g为重力加速度；ρ为密度；δ为表面张力系数；κ为交界面曲率；τ为黏性力，本文采用牛顿流体黏度模型。动量方程最后一项为界面张力源项，采用J.U.Brackbill[10]连续界面力模型(CFS)。

1.3 几何模型、数值方法和边界初始条件

几何模型采用笛卡尔坐标系对内径50 mm，长16 m的三维水平圆管进行模拟，其中壁厚极薄忽略不计，与顾汉洋[11]实验条件相一致，几何模型如图2所示。

图2 几何模型Fig.2 Geometric model

图2 中，入口分层高度比为0.5，空气、水分别通过图中的蓝、红色入口截面恒流速进入水平管道；出口压力控制恒为大气压；对可编译的算例文件进行α、u、初场压强以及空气、水物性的设置，参考王鑫[12]的液塞追踪模型，定义单位长度的相界面张力为0.07 N/m，湍流模型的k、ε设置根据不同工况通过下式计算得到。湍流模型的选择将在后面进行详细讨论。

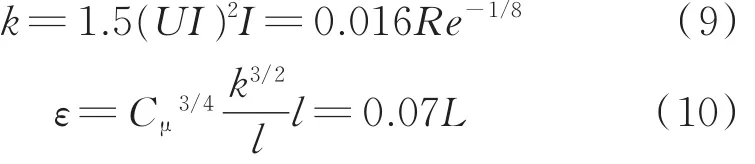
式中，I为湍流强度，l为湍流尺度；L为水力直径；Cμ值为0.09；U为平均速度。

在模型中，时间的离散格式采用一阶隐式欧拉格式；梯度格式采用有限元高斯线性插值；对流项格式采取高斯迎风和高斯线性格式，这些是二阶插值格式，可以保证计算的精度和稳定性；扩散项格式采用二阶高斯守恒格式；表面插值采用中心差分格式；压力的计算采用PCG预处理共轭梯度对称矩阵求解器；速度、湍动能、耗散率的计算采用PBiCG预处理共轭梯度非对称矩阵求解器；体积分数采用光顺求解器下的高斯赛德尔迭代计算。

本文模型采用了OpenFoam独有的PIMPLE算法，即在每个时间步内用SIMPLE稳态算法求解，将每个时间步内看成稳态流动，而时间步长的步进用PISO算法来完成。外循环的压力修正次数设为2，内循环体积分数求解次数设为4，相界面人工压缩项设为保守压缩。

1.4 湍流模型

DNS、LES湍流模型计算效率低，两相流模拟计算中常用的湍流模型有标准k‐ε模型、RNGk‐ε模型、可实现k‐ε模型、k‐ωSST 模型。以Usg=5 m/s、Usl=1 m/s为例(Usg为气相表观速度，Usl为液相表观速度），在相同的网格数和时间步长下对这四种湍流模型进行模拟，得到起塞距离、液塞频率与顾汉洋[12]实验对比，如图3、4所示。从图3、4可以看出，可实现k‐ε模型下的算例与顾汉洋[12]的实验结果最为接近，且符合程度较好，故选可实现k‐ε模型和壁面函数法相结合作为湍流模型。

图3 界面起塞位置模拟与实验值比较Fig.3 Comparision between simulated and experimental value of forming slug position

图4 模拟与实验的液塞频率沿流动方向变化比较Fig.4 Comparision between simulated and experimental value of slug frequency along the fow direction

1.5 网格、时间步长独立性分析

为了在计算中捕捉气液界面的瞬态特征，保证Courant数小于0.5，空间步长Δx为一个定值，根据每个计算时层得到的最大相速度Umax自动调整时间步长Δt。

以Usg=5 m/s、Usl=1 m/s为例，在相同的空间步 长 下对 Courant数 分别 为 0.125、0.250、0.325、0.500进行模拟，如图5所示。从图5中可以看出，时间步长对模拟结果影响不大，为提高计算效率，故选择Courant数为0.500时的时间步长。

采用边界层加密的六面体网格对模型进行划分，为了排除网格稀疏程度对模拟结果的影响，以Usg=5 m/s、Usl=1 m/s为例，分别对空间步长为0.002 0、0.002 5、0.003 0、0.004 0 m 的算例进行模拟，结果如图6所示。由图6可知，网格越小，与实验值越接近，考虑计算效率的影响，最终选择空间步长为0.003 0 m。

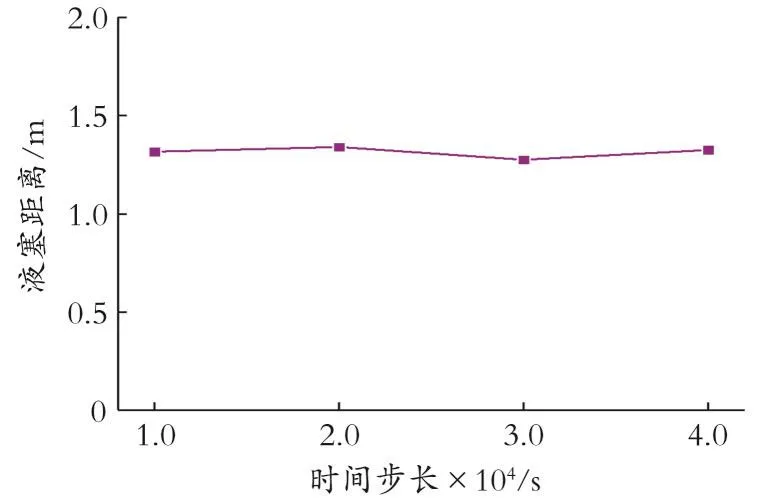
图5 界面起塞位置随时间步长的变化Fig.5 Variation of forming slug position with time step

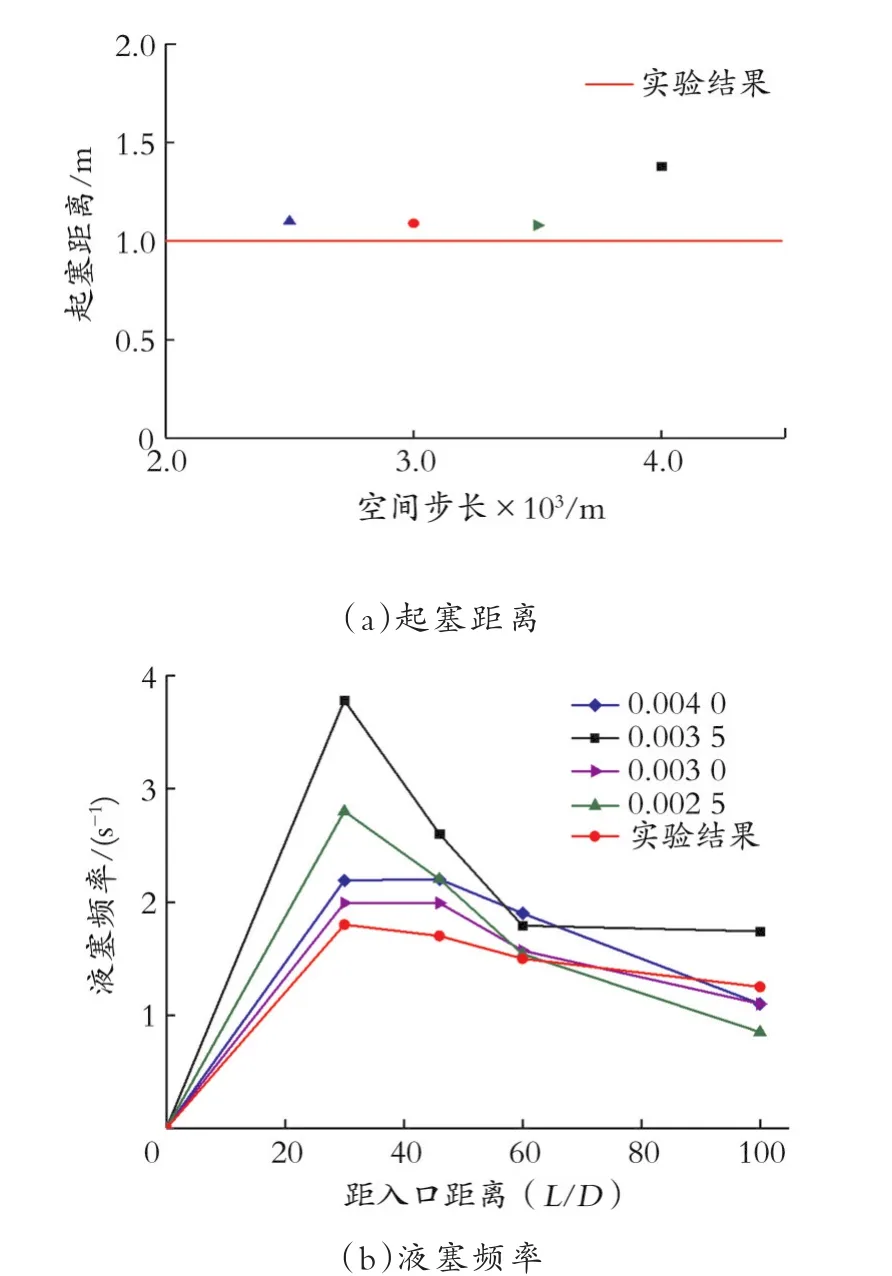
图6 起塞距离、液塞频率随空间步长的变化Fig.6 Variation of forming slug position and slug frequency with space step

2 计算与模型验证

通过上述选定的两相流数值模型，对内径为50 mm的管道进行不同气、液速条件下的气、水两相流模拟。表1为模拟捕捉到的5种不同流型与实验流型的对比。由表1可以看出，模拟的流型与实际较为一致，能很好地反映两相流在不同气液速下的相界面结构特征。

根据表1对不同气液速下的流型进行判断，以气相表观流速为横坐标、液相表观流速为纵坐标，取对数坐标系作流型图，与Mandhane（1974）流型图进行对比，如图7所示。Mandhane流型图以水‐空气的实验数据为基础，适用范围为：管径12.7～165.1 mm，液相密度 705～1 009 kg/m3，气相密度0.8～50.5 kg/m3，液相黏度 3～900 mPa⋅s，气相黏度0.10～0.22 mPa⋅s，表面张力24～103 mN/m，本文的计算模型完全符合条件，且模拟结果基本与Mandhane流型图相一致，验证了该模型对两相流流型模拟的可靠性。

表1 5种流型模拟与实验对比Table 1 Comparison between simulation and experiment of five flow patterns

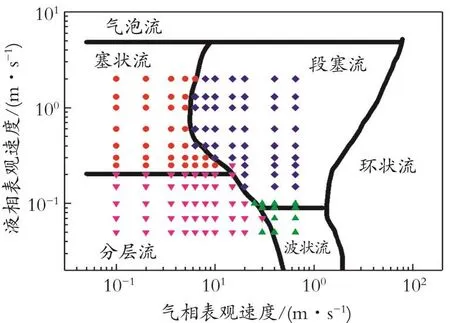
图7 流型模拟结果与Mandhane流型图比较Fig.7 Comparison between of flow pattern simulation and Mandhane flow pattern

图 8为Usg=5 m/s、Usl=1 m/s时，模拟与顾汉洋[11]实验的液塞频率沿流动方向变化的比较。

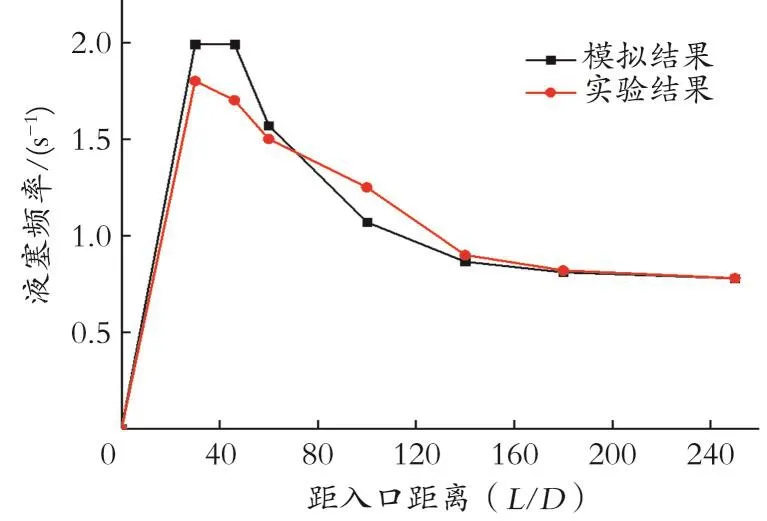
图8 模拟与实验的液塞频率沿流动方向演化比较Fig.8 Comparison between simulation and experiment of slug frequency along the flow direction

从图8中可以看出，模型从定量上得到了模拟与实验相一致的结果，真实地反映了起塞、液塞合并、液塞趋于稳定的现象，证明了该模型对段塞流模拟的有效性。

3 模拟与结果分析

图9为Usg=5 m/s、Usl=1 m/s时管道入口处的起塞过程，在较快流速的气体带动下，形成频率大、振幅小的一系列界面波，气、液之间的动量传递引发界面不稳定，使波迅速增长并相互合并，最终导致界面波频率变小，波长、振幅增大，这与顾汉洋[10]结论相一致。当气体上层流动空间变小，在入口恒流量的情况下，气体加速通过界面波最高点处，由于伯努利效应导致界面波上面空气压力减小，当压差的作用克服了界面张力和重力时，界面波被抬高，界面波的波峰阻塞管道时即产生起塞现象。

图9 Usg=5 m/s、Usl=1 m/s的起塞过程Fig.9 Plugging process ofUsg=5 m/s andUsl=1 m/s

模拟中得到液塞头部向前抛出并卷吸气体的现象与实际高速摄像拍到的液塞头部结构相一致。图10为某一液塞局部的速度矢量、水体积分数和压力分布云图。分析其原因，液体桥塞管道后，液塞后面压力陡升，在液塞前后压差的作用下，液塞顶部液体被快速推出，形成液塞头部向前抛出，在重力的作用下下落，液塞体的动能大于前方液膜区动能，如图10（a）矢量箭头的颜色所示。当液塞吸收液膜中液体时，液膜中液体被加速到液塞速度，在液塞前端形成涡流区，由于涡流的存在，液塞会卷吸部分气体，最终在液塞头部形成一个具有涡流和高动能的气液混合区。这与A.E.Dukler等[13]提出的最短液塞长度物理模型相一致，即液塞速度大于液膜速度，假设液塞静止不动，相当于前方液膜射流进入液塞，在液膜分离点和回流点之间形成涡流，并伴有大量气泡的卷吸，这个区域即为液塞混合区。

表 2分别为Usg=5 m/s、Usl=1 m/s和Usg=3 m/s、Usl=1 m/s时，一个发展中液塞随时间变化的运动过程。从表2中可以看出，气液速差越小，液位越高，液塞长度越长，导致两种工况下的液塞发展过程有所差异。气液速度差较小时，液塞头部抛出现象不明显，液塞在气体推动下速度均衡向前发展，吸收前面液膜，液膜液位波动不大；气液速度差较大时，液塞有明显的抛出现象，液塞通过抛出、下落的周期性运动向前推进吸收液膜。这是因为气、液速度差较大时，液位偏低，发生桥塞的液量较小，在高速气流的推动下液塞头部向前抛出，液体与管子上部出现空隙，气体加速通过，液体再次被抬起，液塞以此种方式循环向前运动。而气、液速度差较小时，液位较高，液塞体长，在气体的推动下，液塞体较均匀向前运动。

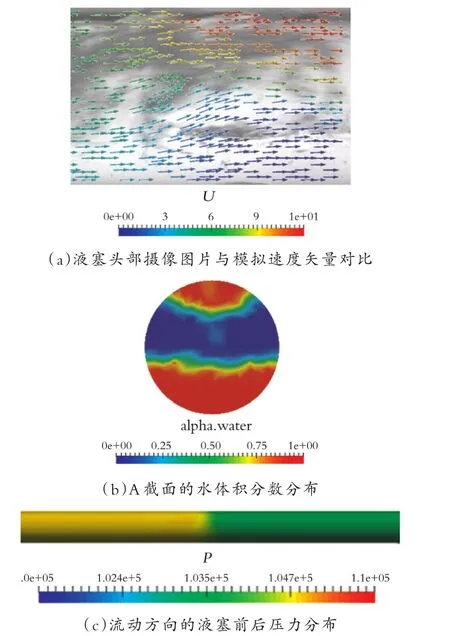
图10 液塞局部的速度矢量、水体积分数和压力分布Fig.10 Distribution of the velocity vector,water volume

表2 不同气、液速度差下某一发展中液塞随时间的变化Table 2 Variation of a developing slug with time at diffie⁃rent gas⁃liquid speed difference

图11为Usg=5 m/s、Usl=1 m/s时某一液塞不同截面处速度分布云图和径向速度曲线。图11可知，液塞顶部液体速度大于底部液体速度，液塞头平均速度大于液塞尾平均速度，很好解释了液塞是通过头部的液体卷吸和尾部的液体流出不断向前运动的。

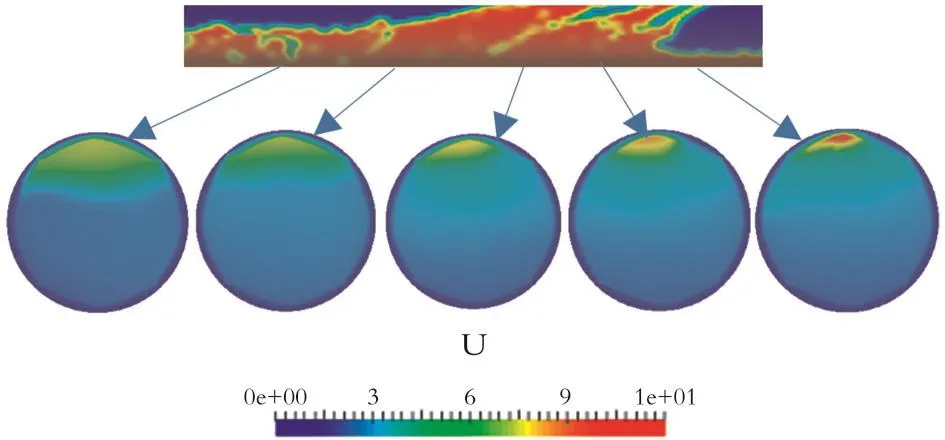
图11 液塞不同截面处速度分布Fig.11 Cloud chart of velocity distribution at different sections of liquid plug

气体的推动使液塞上半部分速度接近气速，而下半部分由于受液体和壁面剪切力控制，液速略大于液膜速度，因此可以说明，液塞运动速度主要由液塞头部和上半部分的液体速度决定，这与波的传播方式极为相似，液塞的形成、发展和运动过程可以看作管道入口的气液速度差引起的扰动形成界面波，界面波进行合并、增长，由于受封闭空间限制，最终桥塞形成液塞，液塞以一种变相波的方式向前运动。

4 结 论

本文建立的模型能够有效预测气、液两相流流型及相界面结构特征，对于流动较为复杂的段塞流流型，能够真实地反映出起塞、液塞的成长、演化过程以及段塞流的瞬态流动特性，从定性、定量两个角度证明了该模型的有效性。

在气体的带动下，管道入口形成频率大、振幅小的一系列界面波，界面不稳定使波迅速增长并相互合并，最终导致界面波频率变小，波长、振幅增大，当界面波的波峰阻塞管道时即产生起塞现象。在气体推动下，液塞头部速度大于前方液膜速度，液塞头向前抛出并下落，在液膜、液塞交界处形成涡旋，卷吸大量气体形成液塞混合区。

气液速度差较小时，液塞头部抛出现象不明显，液塞在气体推动下速度均衡向前发展吸收前面液膜，液膜液位波动不大；气液速度差较大时，液塞有明显的周期抛出现象，液塞通过抛出、下落的周期性运动向前推进吸收液膜。

液塞顶部液体速度大于底部液体速度，液塞头平均速度大于液塞尾平均速度，液塞以头部液体卷吸和尾部液体流出不断向前运动。液塞上半部分速度接近气速，而下半部分速度略大于液膜速度，液塞运动速度主要由液塞头部和上半部分的液体速度决定，并以一种变相波的方式向前运动。