储层岩石的三维逾渗模型研究

苏 崭，李 玮，黄红亮，王旭东，郑智冬

（1.东北石油大学石油工程学院，黑龙江大庆163318；2.渤海钻探工程有限公司第五钻井分公司，河北河间062465；3.中海油研究总院有限责任公司海洋石油高效开发国家重点实验室，北京100028；4.渤海钻探第三钻井工程公司，天津300280）

储层中流体的流通状况是制定油田开发方案的重要依据，它对提高采收率具有重要作用。裂缝性地层中的裂缝是流体流动的主要通道，研究裂缝连通情况对储层渗流特性的影响，一直是油田开采领域的一个难点。随着时代的发展，计算机技术在油田中的应用也愈加广泛。许多在现实中难以实现的实验、难以验证的猜想，都可以用计算机进行模拟。计算机模拟已成为除实验外解决问题最为有效的手段。

随着介质中的孔隙被随机堵塞，孔隙度减小，渗透率变差。当孔隙度下降到某一临界值Pc时，介质由可渗透转变为不可渗透，这种现象被定义为逾渗。逾渗模型是一种描述流体在无序介质中随机流动的数学模型。彭自正等[1]利用计算机建立了岩石的二维逾渗模型。冯增朝等[2]详细研究了二维条件下带裂缝介质的逾渗机制，建立了二维逾渗规律研究模型。朱大勇等[3]基于二维逾渗模型，用相同尺寸的均匀网格划分岩石，并使每个连接节点的键具有相同的连通概率，研究逾渗模型中渗透概率递推矩阵。康志勤等[4]基于显微CT技术研究了三维孔隙结构的逾渗规律。以上研究运用不同方法建立了逾渗模型，从不同角度研究逾渗规律。现实中的逾渗发生在三维物体中，二维模型模拟结果不够直观、精确。目前三维逾渗模型的建模方式较少，对逾渗规律的认识也不够深入。

本文运用MATLAB建立三维逾渗模型，将储层岩石理想地看作由均匀网格划分的规则多孔介质。与传统的研究方法不同，它从多孔介质的微观角度出发，将其视为键和节点组成的网络体。此模型能够模拟裂缝连通团的分布情况，得出均匀多孔介质的逾渗规律；描述岩石的形状、大小对其内部流体流动的影响，对高效开发油藏具有重要的意义。

1 三维逾渗模型的建立

1.1 构建模型的思路

逾渗理论研究的是多孔介质由于内部连接程度的改变所引起的渗透状态的改变，即多孔介质由不渗透到渗透的过程。裂缝被视为流体流通的通道，裂缝之间的相互连接使其“丛集”最终达到“贯通”[5]。建立三维逾渗模型，首先将所研究的储层岩石理想化为一个规则的长方体，然后用均匀网格划分长方体。将储层中的裂缝视为逾渗网格中的节点，裂缝之间的连接情况用逾渗网格中的键来表示。每个键都有一定的“连通概率（P）”，被键连接到一起的节点构成一个簇，即逾渗集团。

由逾渗的定义可知，流体在多孔介质中流动时，若介质被随机堵塞，一旦被堵塞的比例达到某个值，多孔介质就会由可渗透转变为不可渗透。也就是说，存在着一个临界值，使模型是否可渗透的状态发生改变，这个临界值被称为逾渗阈值。

1.2 构建模型的方法

逾渗主要分为键逾渗和点逾渗。键逾渗是指所有的节点都是通的，每条键以概率P连通；点逾渗是指所有的键都是连通的，节点有可能通有可能不通，通过的点叫作被占据的点。本文中的模型以键逾渗理论为基础。

三维点阵的节点之间的键有两种状态：连通或不连通，每个键连通的概率是P，不连通的概率是（1-P），每个键的连通状况与相邻的键无关。在三维点阵上，每个节点周围有六个节点与之相邻，假设每个节点代表相同的裂缝，可以认为每个簇的大小仅由内部的节点数量确定，这样就建立了三维逾渗模型[6]。当连通概率达到某个值时（即逾渗阈值），三维点阵上就会形成使模型可渗透的簇，即渗流集群。

假设模型中键的连通概率（P）取值0.01～0.90，模型的长、宽、高分别用n1、n2、n3表示。设计五种不同尺寸的模型N1-N5进行模拟，如图1所示。其中，N1、N2、N3的尺寸等比例增大，N2、N4、N5的节点数相近，几何形态分别为长方体、正方体和扁长方体。

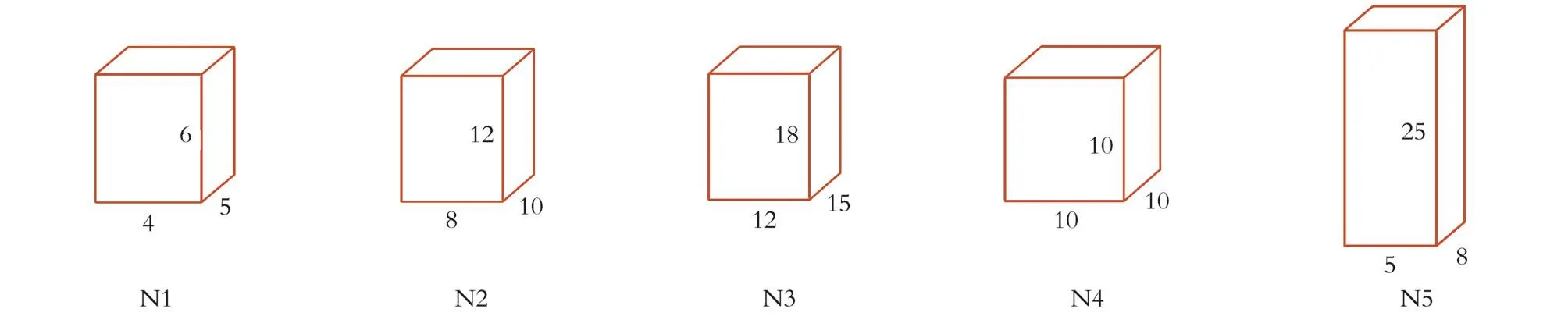
图1 五种不同尺寸模型Fig.1 Five different size models

随着连通概率（P）的改变，N1、N2、N3模型的簇的分布情况如图2所示，其中蓝点代表节点，黑色、绿色、红色的线分别代表节点之间x、y、z三个方向的键。模型能较直观地反映多孔介质的内部连接情况，还能得到不同连通概率下，每个模型中各个尺寸的簇的数量和最大簇。

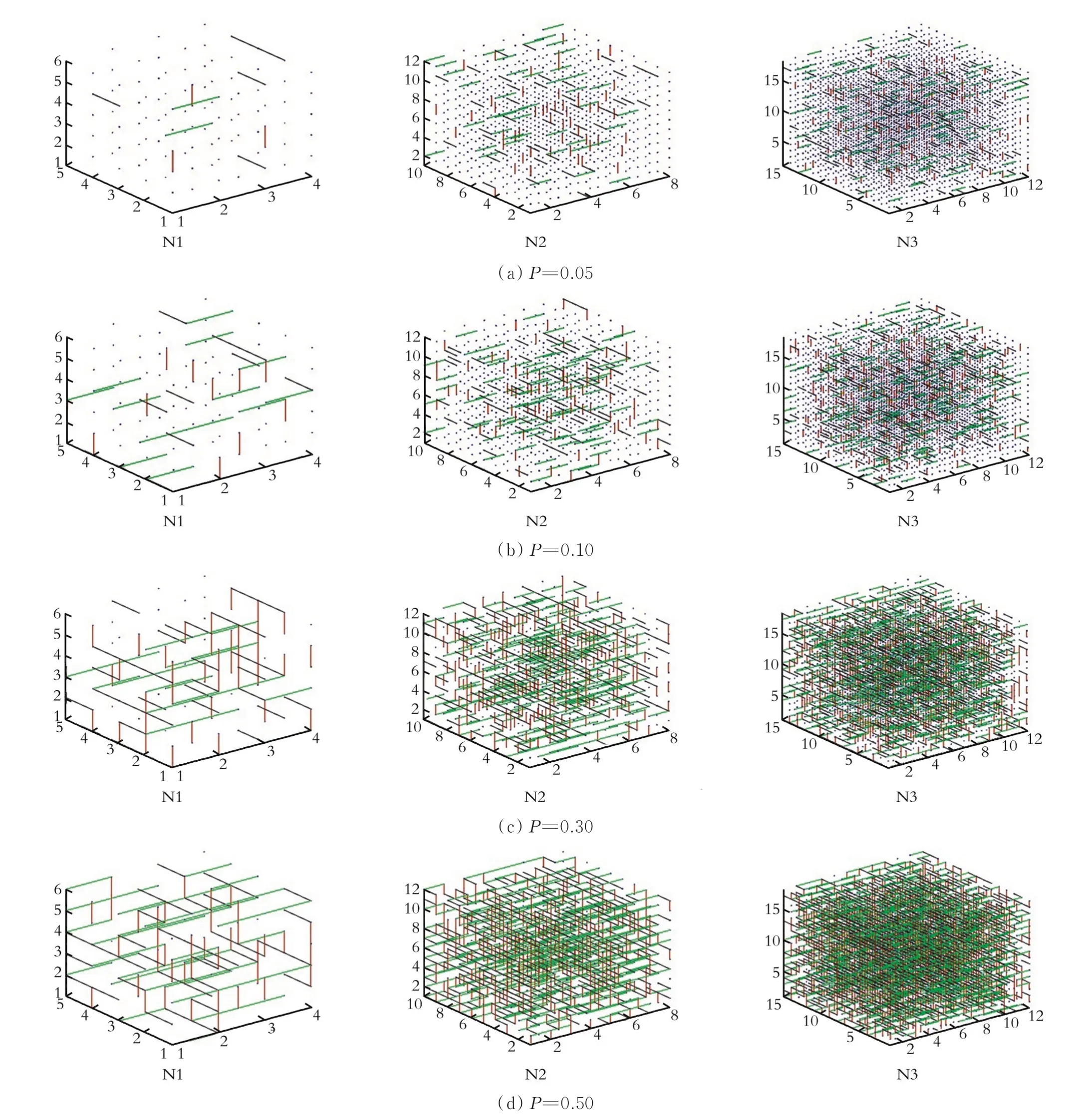
图2 不同尺寸模型的簇分布情况Fig.2 Cluster distribution of different size models

由不同尺寸的簇的数量可以计算出孔隙率和平均簇，计算孔隙率的公式为：

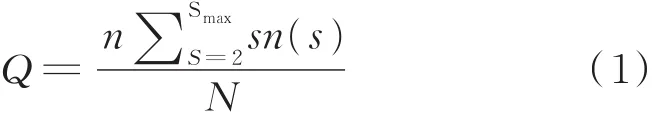
式中，Q 为孔隙率；s为簇的大小；Smax为最大簇；n（s）为簇大小为s的簇的个数；N为模型总节点数。

计算平均簇的公式为：

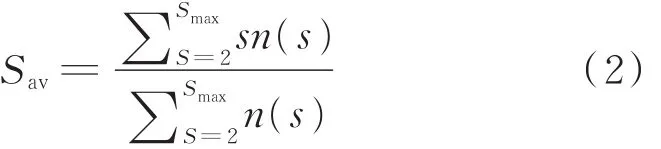
式中，Sav为平均簇。

相互连接的节点形成的集团称为簇，一个簇至少包含两个节点，节点数最多的簇为最大簇[7]。逾渗概率为最大簇节点数与总节点数的比值，它可以作为判断多孔介质渗透性优劣的依据，是逾渗问题的一个重要概念。

计算逾渗概率的公式为：

式中，Yg为逾渗概率；Nmax为最大簇节点数。

2 模型模拟结果的分析

2.1 连通概率对总簇数的影响

模型可以模拟得出多孔介质中的总簇数。在不同尺寸的模型中，改变连通概率进行模拟，其对应的总簇数如表1所示，两者的关系如图3所示。

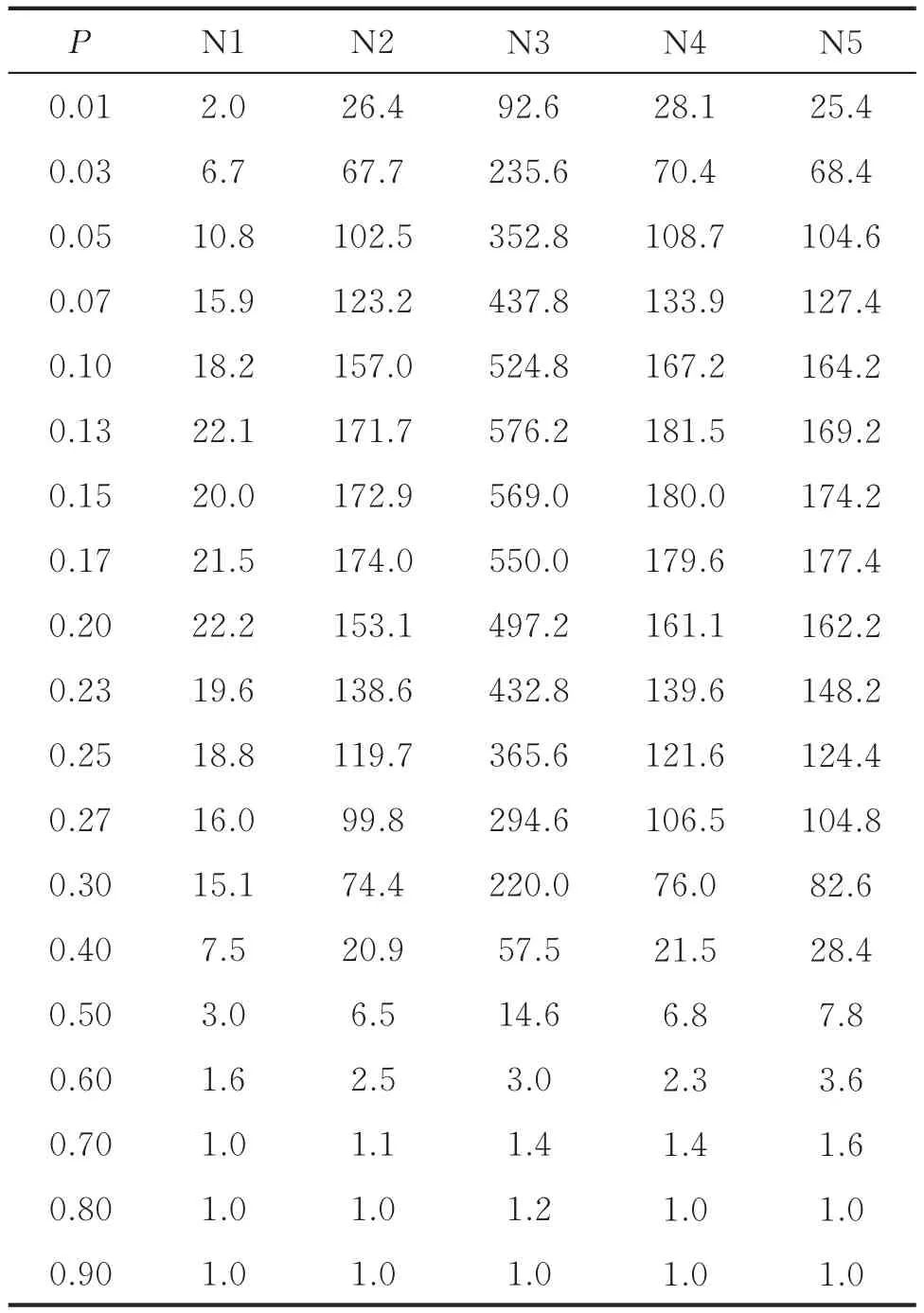
表1 总簇数Table 1 Total number of clusters

图3 不同尺寸模型总簇数与连通概率的关系Fig.3 Relationship between total cluster number and P of different size models

由图3可知，当连通概率较小时，相互连接的节点少，聚集程度低，难以形成簇。随着连通概率增加、模型尺寸增大，总簇数增加得越快。此时节点之间快速连接形成簇，虽然已经形成的簇有可能会连接成一个新簇，使总簇数减少，但总体来说，总簇数还是呈增加趋势。此时连通概率继续增加，已经形成的簇相互连接，总簇数的增长变缓[7]。当连通概率达到一定值时，总簇数开始随连通概率的增加而减少，这是因为簇之间连接的趋势初始阶段大于单个节点之间连接的趋势。

N1、N2、N3模型尺寸不同，其总簇数与连通概率的关系曲线有较大差别，但曲线峰值对应的连通概率相同，均为0.17。N2、N4、N5的曲线基本重合，说明总簇数只与模型的尺寸有关，与模型的形状无关。

2.2 孔隙率与逾渗概率的关系

孔隙率可以用式（1）计算，当可渗透的多孔介质被随机堵塞时，多孔介质的孔隙率下降，多孔介质由可渗透转变为不可渗透[8]。用孔隙率可以粗略评价介质的渗透性。不同连通概率下，N1-N5模型的孔隙率如图4所示。

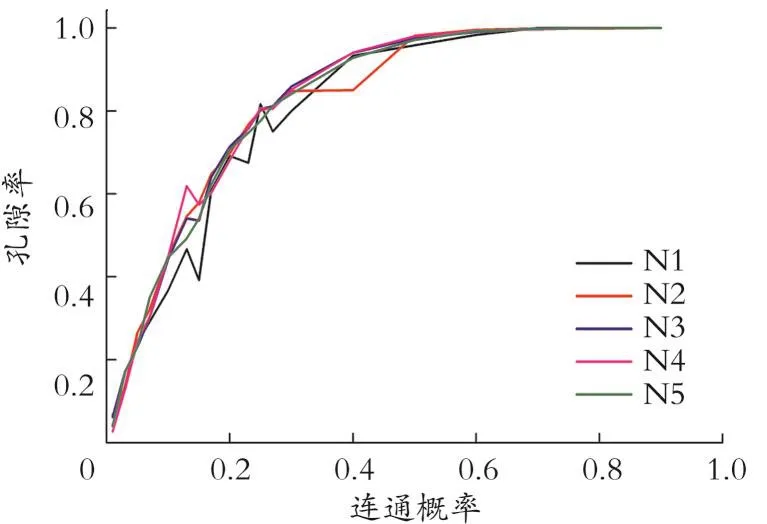
图4 不同尺寸模型孔隙率与连通概率的关系Fig.4 Relationship between porosity and P of different size models

对不同尺寸的模型，在不同连通概率下进行模拟，得到最大簇，运用式（3）计算逾渗概率。同一连通概率下，孔隙率和逾渗概率的关系如图5所示。

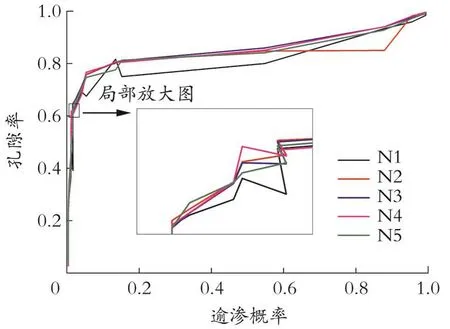
图5 孔隙率和逾渗概率的关系Fig.5 Relationship between porosity and percolation probability

由图5可知，连通概率小于0.20时，孔隙率和逾渗概率之间的关系没有规律性。逾渗概率的大小反映了多孔介质内部最大簇的分布程度，可避免因过多统计对渗透性无贡献的“小级别死端及封闭裂缝”而造成的对多孔介质渗透性优劣的误判[8]。逾渗概率可以对多孔介质的渗透性进行判断，比孔隙率更为准确。

2.3 连通概率对逾渗概率的影响

不同连通概率下，N1-N5模型的逾渗概率如图6所示。由图6可知，不同尺寸、不同形状的模型，其逾渗概率随连通概率的变化呈现相同的趋势。当连通概率较小时，逾渗概率增加比较缓慢，对N1、N5模型来说，当连通概率超过第一临界值0.30时，逾渗概率突然大幅度增加，当连通概率超过第二临界值0.70时，逾渗概率再次开始缓慢增加并最终趋近于1。

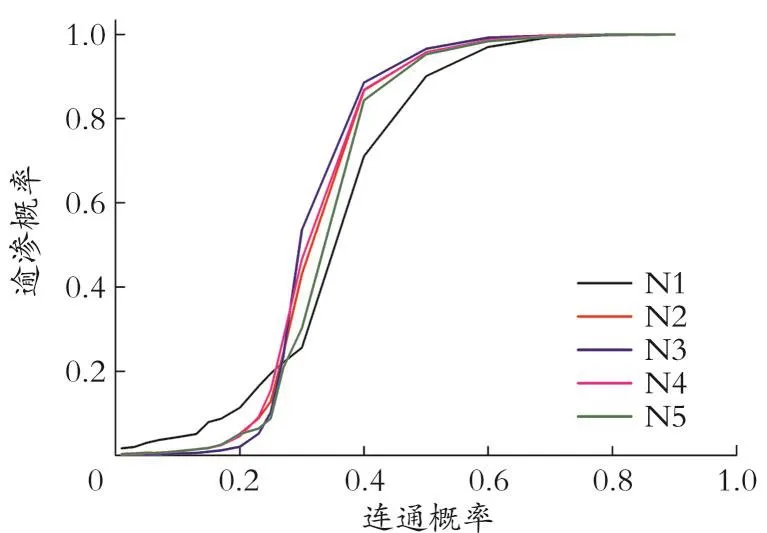
图6 不同尺寸模型逾渗概率与连通概率的关系Fig.6 Relationship between percolation probability and P of different size models

对N2、N3、N4模型来说，当连通概率超过第一临界值0.25时，逾渗概率突然大幅度增加，当连通概率超过第二临界值0.60时，逾渗概率再次开始缓慢增加并最终趋近于1。

当连通概率小于第一临界值时，单个节点之间连接的趋势较小，逾渗概率的增长率较小；当连通概率在第一、第二临界值之间时，簇与簇之间迅速连接形成更大的簇；当连通概率大于第二临界值时，节点与簇的连接状态比较稳定，逾渗概率增加较为缓慢，最终趋向于 1[9‐10]。

2.4 连通概率对渗流集群的影响

在实际应用中，用逾渗概率判断多孔介质是否可渗透存在一定误差。本模型提出了渗流集群的概念，渗流集群是可以使多孔介质渗透的簇，它可以准确判断介质是否可渗透，精准捕捉逾渗阈值。本模型中，逾渗阈值指的是当多孔介质由不渗透转变为渗透时对应的连通概率，即渗流集群≥1时对应的连通概率。不同连通概率下，N1-N5模型的渗流集群如图7所示。渗流集群等于0时，模型不可渗透；渗流集群在0～1时，模型有渗透的可能，且渗透的可能性随着渗流集群数值的增大而增大；渗流集群等于或大于1时，模型一定可渗透。

图7 不同尺寸模型渗流集群数与连通概率的关系Fig.7 Relationship between the number of seepage clusters and the P of different size models

由图7可以看出，N1-N5模型的渗流集群开始大于0时对应的连通概率分别是0.05、0.10、0.17、0.10、0.07，即五个模型各自的逾渗阈值。对于N1、N2、N3来说，模型尺寸越大，逾渗阈值就越大；对于N2、N4、N5来说，N5的几何形状较为特殊，有一个较小的面，因此其逾渗阈值小于N2、N4。

五条曲线的最大值都不相同，N3最大，N1最小，N2、N4、N5相近可看作一类。可知模型尺寸越大，节点越多，可形成渗流集群的上限越高，反映到图像中就是曲线的最大值越大。

随着连通概率的增加，不管是何种尺寸、何种形状的模型，渗流集群的数量最终都会趋向于1。因为当连通概率达到一定值时，模型内的节点连接状况趋于稳定，最终会形成一个渗流集群。

在图线波动阶段，尺寸越小的模型波动得越剧烈。因为尺寸小的模型节点少，由连通概率所导致的连接不确定性比较明显[11‐12]。

2.5 平均簇与连通概率之间的关系

对N1-N5模型进行模拟，可以得出各个尺寸的簇的个数，将得到的数据代入式（2），可计算平均簇，绘制图8。由图8可以看出，连通概率小于0.5时，平均簇比较小且增长缓慢；连通概率在0.5～0.8时，平均簇的增长率突然变大，这是因为簇与簇之间迅速连接，使簇的尺寸变大，簇的个数变少；当连通概率大于0.8时，节点之间的连接状况趋于稳定，平均簇大小的增长率有所缓和。

2.6 对错误逾渗规律的否定

对N1-N5模型在相同的连通概率下多次模拟，可以明确一些容易误判的逾渗规律。

2.6.1 最大簇与平均簇的关系 在同一模型、同一连通概率下多次模拟，得到图9所示结果。

图8 模型平均簇大小与连通概率的关系Fig.8 Relationship between model average cluster size and P

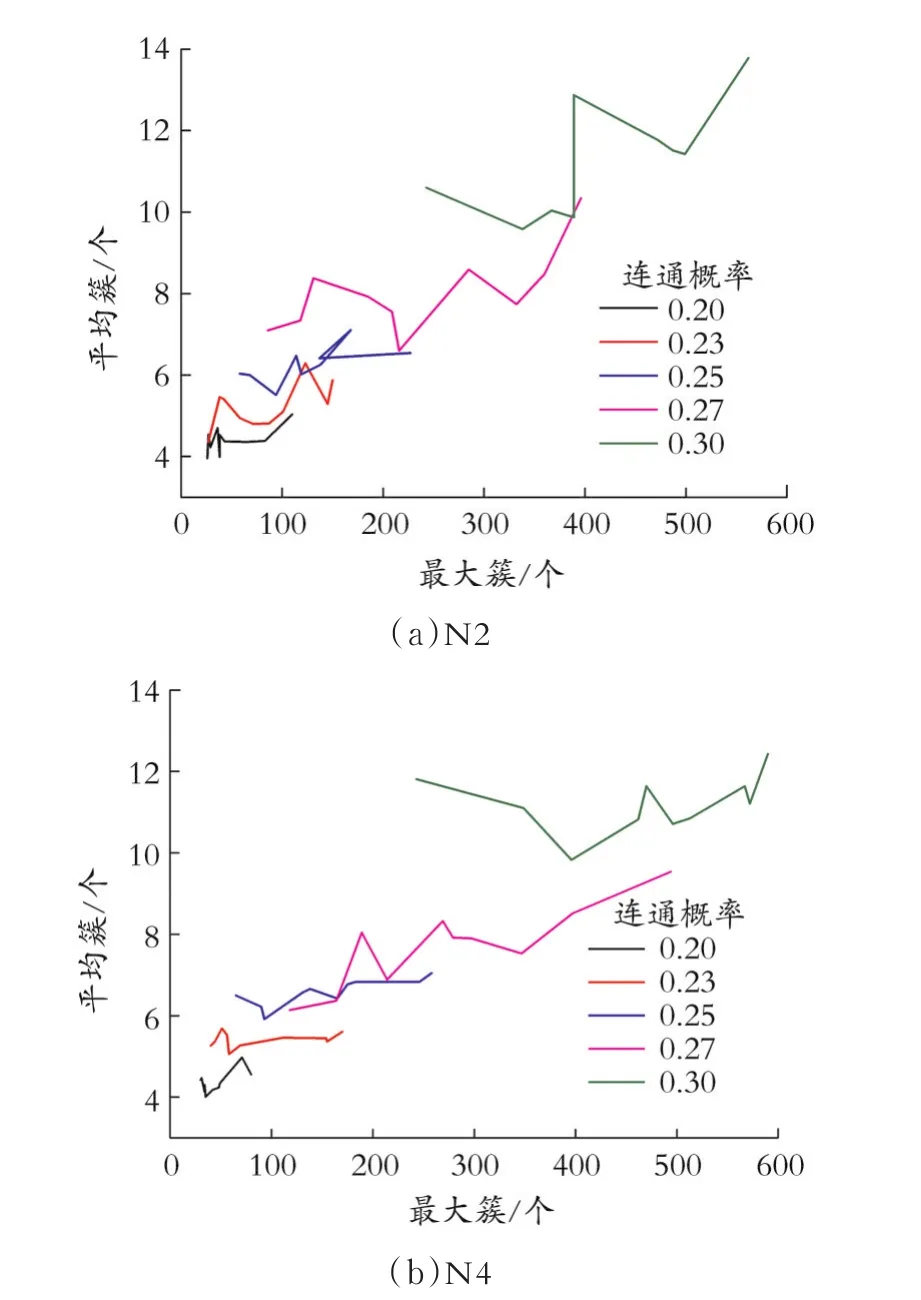
图9 最大簇与平均簇间的关系Fig.9 Relationship between the largest cluster and the average cluster size

由图9可以看出，平均簇和最大簇的大小随着连通概率的增加总体呈增加趋势。在同一模型，同一连通概率下多次模拟，可以得知最大簇和平均簇之间的关系没有明显的规律性。

2.6.2 最大簇与总簇数的关系 在同一模型、同一连通概率下多次模拟，得到的结果如图10所示。由图10可以看出，最大簇的大小随着连通概率的增加总体呈增加趋势，总簇数随着连通概率的增加总体呈减少趋势。在同一模型，同一连通概率下多次模拟，可以得知最大簇和总簇数之间没有明显的规律性。

图10 最大簇与总簇数的关系Fig.10 Relationship between the largest cluster and the total number of clusters

3 结 论

（1）本文所建立的三维逾渗模型能够模拟多孔介质中由于连通概率变化所引起的长程联结性突变。它能模拟裂缝连通团的分布情况，得出均匀多孔介质的逾渗规律、逾渗阈值，并判断其是否可渗透，模型模拟的结果与其它模型模拟结果及实验结果基本一致并有了一定的优化。

（2）在连通概率从0开始增加的初期，随着连通概率增加，单个节点之间相互连接形成簇，总簇数增加。当连通概率增加到0.17后，总簇数开始减少。总簇数的变化规律只与介质的尺寸有关，与介质的形状无关。

（3）孔隙率、逾渗概率都可以作为判断多孔介质渗透性的依据，逾渗概率可避免过多统计对渗透性无贡献的“小级别死端及封闭裂缝”，因此更为准确。当连通概率较小时，逾渗概率随着连通概率的增加而缓慢增加，当连通概率超过第一临界值时，逾渗概率的增加幅度突然增大，当连通概率超过第二临界值时，逾渗概率再次开始缓慢增加且最终趋近于1。

（4）渗流集群可以准确地判定多孔介质是否可渗透，精准捕捉逾渗阈值。N1-N5模型的渗流集群开始大于0时对应的连通概率分别是0.05、0.10、0.17、0.10、0.07，即五个模型各自的逾渗阈值。逾渗阈值的大小与介质的尺寸和形状都有关，尺寸越大，逾渗阈值就越大；当尺寸相同时，若介质有一个较小的面，逾渗阈值就会较小。

（5）最大簇与平均簇、最大簇与总簇数的关系之间没有明显的规律性。