周向波纹圆柱壳屈曲特性试验研究
2020-06-30吴海建张山李胜秋
吴海建 张山 李胜秋

摘 要:本文研究了在均布外压作用下,周向波纹圆柱壳的非线性屈曲问题,以及波纹幅值对屈曲的影响。首先,采用3D打印技术制作了6个树脂波纹圆柱壳,相同幅值的模型均打印了2个,测量了其真实壁厚和真实圆柱壳的几何形状,并进行静水压力试验,然后用专业软件对真实圆柱壳体进行非线性分析。有限元计算和试验结果一致表明,随着波纹幅值的增大,圆柱壳抵抗屈曲变形的能力也随之增大,并且真实圆柱壳的后屈曲失稳模式与试验模型的破坏形式一致。
关键词:柱形壳 周向波纹 屈曲 静水压力试验 有限元分析
中图分类号:P755.2 文献标识码:A 文章编号:1674-098X(2020)03(c)-0089-03
Abstract: The paper focuses on the nonlinear buckling of circumferentially corrugated cylindrical shells under uniform external pressure, along with the effects of corrugation form and amplitude on the buckling. First, 6 resin corrugated cylindrical shells are produced using 3D printing technology, two models of the same amplitude are printed, the true wall thickness and the geometry of the real cylindrical shell are measured, and hydrostatic pressure tests is performed.. Then, then the nonlinear analysis of the real cylindrical shell is carried out by professional software. The results of finite element calculation and experiment consistently show that as the amplitude of the corrugation increases, the ability of resisting buckling deformation of cylindrical shell increases, and the post-buckling instability mode of the real cylindrical shell is consistent with the failure mode of the experimental model.
Key Words: Circular cylindrical shell;Circumferential corrugation;Buckling;hydrostatic test;Finite element analysis
潜水器是深海探测重要科学工具,耐压壳是潜水器的关键部件,其重量占潜水器总重的1/4-1/2[1],它能承受海水的巨大压力,为工作人员提供安全的工作环境,使设备正常工作。柱形壳是一种常用的耐压结构,其特点是空间利用率高、流体运动阻力小、制造方便。但是这些圆柱壳在承受外压时容易发生屈曲,往往导致无法恢复的坍塌。
一般来说,存在许多提高圆柱壳屈曲能力的方法。首先,改变子午线形状是一种有效的方法。例如,Blachut和其同事研究发现等质量的桶形壳具有比未加筋圆柱壳更高的屈曲能力[2-3]。最近,張建等人,研究了卵形壳及其在海洋工程中的应用[4-5],发现长卵形压力壳对屈曲行为具有有效的抵抗。另一种方法是添加加强筋或波纹来提高圆柱壳的屈曲能力[6-7]。在这些加强方法中,波纹加强是最优的选择,其不需要额外的加强筋就能够提高柱形壳的屈曲能力。Ross等[8]对周向波纹圆柱形耐压壳的非线性屈曲进行了理论、数值和试验研究,Ghazijahani等[7]采用试验法研究了波纹个数对周向波纹圆柱壳屈曲特性的影响。但是,上述研究都是基于相同幅值的波纹柱壳,对不同幅值的波纹柱壳研究较少。
因此,本文讨论了静水压力作用下波纹圆柱壳的幅值对其屈曲特性的影响。采用3D打印技术制作了6个树脂波纹圆柱壳,用三维扫描技术获得真实的波纹柱壳三维模型,并测量壳体的壁厚;然后进行静水压力试验,并采用有限元法计算真实柱壳的非线性屈曲特性;结果表明,试验结果与有限元计算吻合良好。
1 试验研究
1.1 选择材料与加工方法
考虑到模型的加工便捷,试验模型采用3D打印技术,选择树脂作为波纹圆柱壳的打印材料,弹性模量:E=2122.92MPa,泊松比μ=0.3284;密封盖材料:弹性模量E=207GPa、泊松比μ=0.3。如图1所示,模型的直径D=160mm,高度H=230mm,壁厚t=2mm,正弦波纹均匀的分布在柱壳上,波纹幅值h=0,2.5,5(当h=0时柱壳是光柱),波纹跨距S=20mm,密封盖厚度T=10mm。如图2,为了证明试验的可重复性,相同参数的模型均打印了2个,一共打印了6个模型。选择金属板材作为柱壳的密封盖,用高强度胶水将柱壳与密封盖粘结在一起。
1.2 厚度测量与轮廓测量
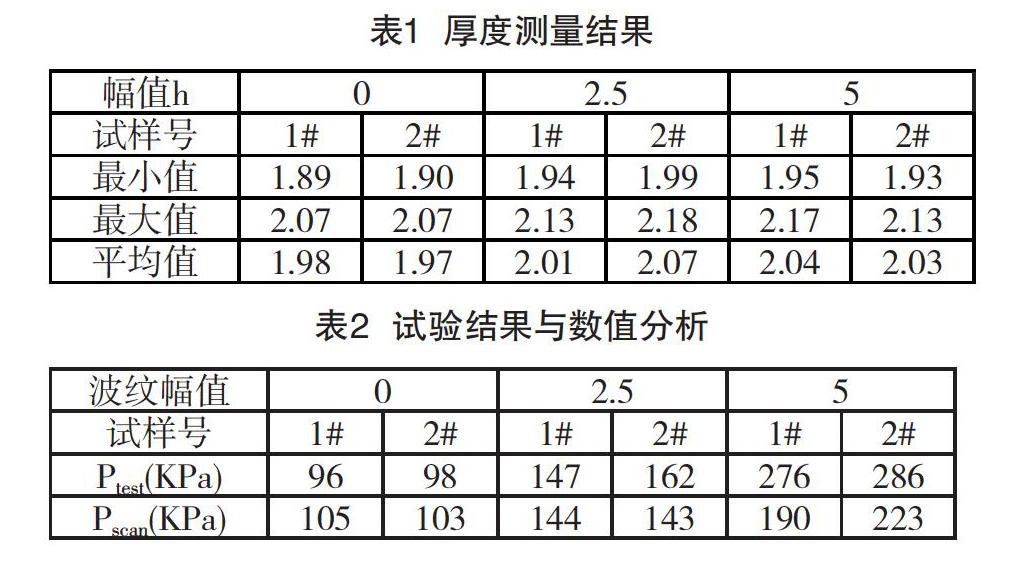
使用超声波测厚仪,对制作好的6个柱壳进行厚度测量,为了保证数据的准确性,每个柱壳测量200个数据点,结果如表1所示,相同幅值下的柱壳平均厚度比较相近,说明同种类型的柱壳打印出来的试样精度很高,波纹幅值相同柱壳在试验中具有相互参考性。
利用手动三维扫描仪,对已经制作好的6个柱壳进行手动扫描,获取圆柱壳外轮廓的真实三维模型。
1.3 静水压力试验
厚度测量与轮廓测量完成后,将模型放入压力舱中,将压力舱密封起来,进行静水压力试验。用水作为加压介质,手动液压泵为加载装置。考虑到试验的对象为树脂圆柱壳,破坏压力很小,要用手动加压泵缓慢加压,待听到因模型破裂而发出声音后停止加压,打开压力舱上的密封盖取出被测模型。
试验获得各个模型破坏载荷Ptest列于表2中;由表2可知,当波纹幅值h=0,2.5,5时,柱壳的试验破坏载荷Ptest分别为96kPa、98kPa,147kPa、162kPa,276kPa、286kPa;相同参数柱壳的试验破坏载荷之间误差很小,这直接证明模型制作精度高、可重复性好;试验破坏载荷随波纹幅值增大而增大,波纹幅值h=0,5时,试验破坏载荷分别为最小值、最大值。如图3所示,试样的破坏位置均中间部位。
2 有限元分析
2.1 划分网格
ANSA是一款通用CAE前处理软件,它具有强大的有限元网格前处理功能。将1.2节中扫描获得的真实外轮廓模型导入到ANSA软件中进行网格划分。因扫描获得的模型是由多个曲面拼接而成,所以使用自由划分网格的方式,网格类型以四边形壳单元S4为主,会出现少量的三角形壳单元S3。
2.2 有限元模型建立
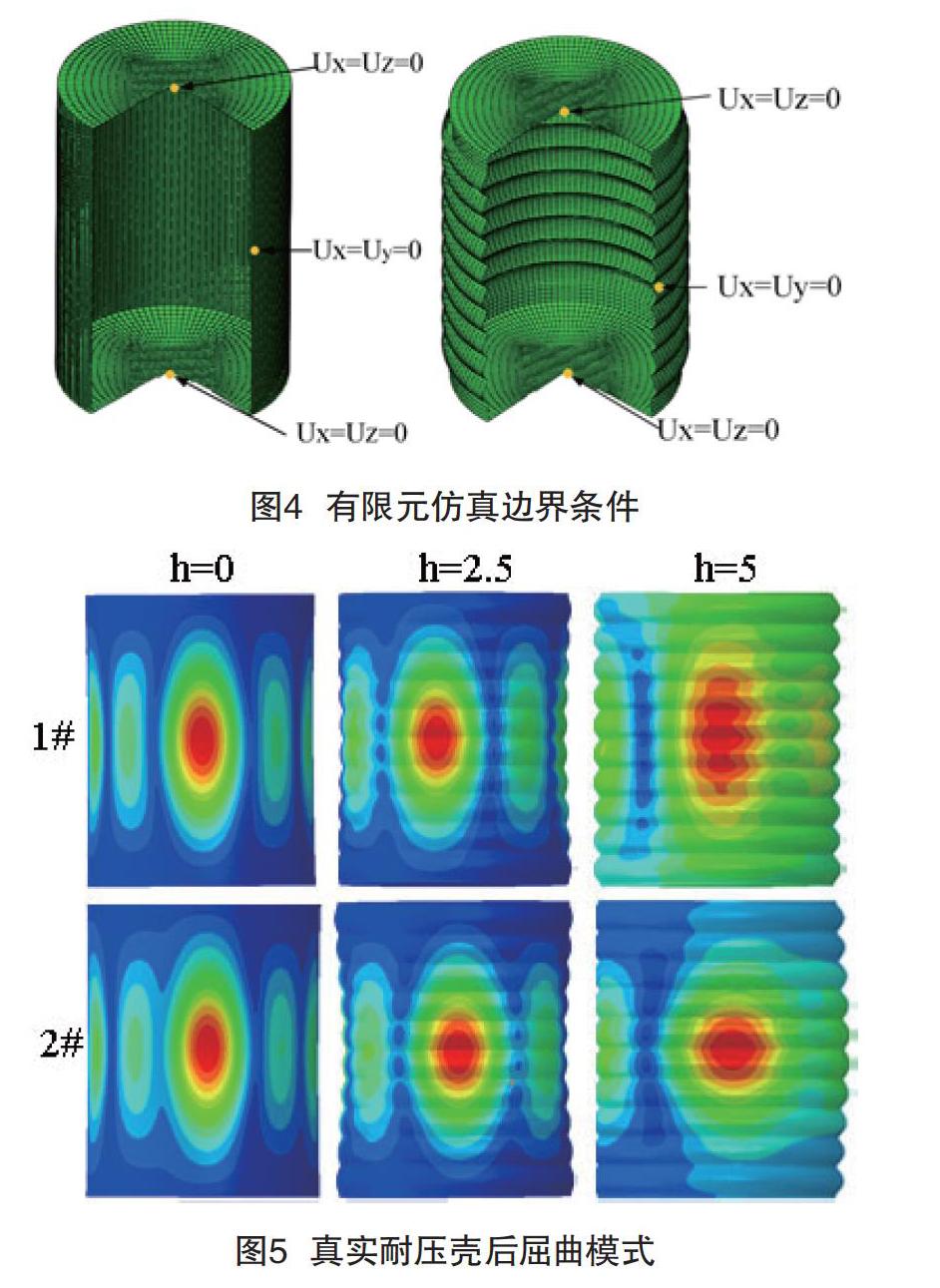
选择ABAQUS作为有限元分析软件,将ANSA软件中处理好的模型导入ABQQUS中,选用与1.1节相同的材料。选择弧长法对真实波纹柱壳进行非线性屈曲分析。设置模型的外压为p=1MPa,模拟静水压力试验。对耐压壳体整体进行分析时,壳体需要3个支撑点,约束6个位移分量[9],边界条件如图4所示,最后对真实壳体进行有限元分析。
2.3 真实壳体非线性屈曲结果分析
图5是真实圆柱壳体的后屈曲模式,壳体发生屈曲的位置都是在其中部,与试验的破坏形式一致。由表2中可知,当波纹幅值h=0,2.5,5时,真实波纹圆柱壳的临界屈曲载荷Pscan分别为105kPa、103kPa,144kPa、143kPa,190kPa、223kPa;相同参数柱壳临界屈曲载荷之间误差很小,Pscan随着波纹幅值增大而增大,波纹幅值h=0,5时,壳体的临界屈曲载荷分别为最小值、最大值。
2.4 对比分析
文章对波纹圆柱壳进行了试验分析与数值分析。波纹幅值h=0时,柱壳的试验结果与有限元仿真相差分别为9.38%和5.10%,试验结果相差2.08%,仿真结果相差1.94%;波纹幅值h=2.5时,试验结果与有限元仿真相差分别为2.08%和13.29%,试验结果相差10.2%,仿真结果相差0.69%;试验结果与有限元仿真之间的误差、试验之间的误差、有限元仿真之间的误差都很小,属于正常范围内。当波纹幅值h=5时,柱壳的试验结果与有限元仿真的趋势相同,但两者间的误差较大;误差主要来自壳模型材料的选取,三维扫描仪的扫描精度以及波纹幅值的选取。由图3 和图5可知,试验模型的失稳位置与有限元仿真的失稳位置吻合良好,均发生在圆柱壳的中间部位。综上所述,当柱壳采用波纹加强方式后,其抵抗屈曲的能力显著提高。
3 结论
(1)试验结果表明,随着波纹幅值的增大,圆柱壳抵抗屈曲变形的能力也随之增大。
(2)有限元结果表明,真实柱壳的后屈曲失稳模式与试验模型的破坏形式一致,吻合度较高。
参考文献
[1] Zhang J, Zuo X L, Wang W B. Overviews of investigation on submersible pressure hulls[J]. Advances in Natural Science, 2014, 7(4): 54-61.
[2] Blachut J, Wang P. Buckling of barreled shells subjected to external hydrostatic pressure[J], Journal of Pressure Vessel Technology, 2001,123(2): 232-239.
[3] Blachut J. Buckling of externally pressurised barrelled shells: a comparison of experiment and theory[J], International Journal Pressure Vessels. Piping, 2002(79): 507-517.
[4] Zhang J, Wang M L, Wang W B, et al. Buckling of egg-shaped shells subjected to external pressure[J]. Thin-Walled Structures, 2017(113): 122-128.
[5] Zhang J, Wang M L, Wang W B, et al. Investigation on egg-shaped pressure hulls[J]. Marine Structures, 2017(52):50-66.
[6] Ghazijahani T G, Jiao H, Holloway D. An experimental study on externally pressurized stiffened and thickened cylindrical shells[J]. Thin-walled Structures, 2014(85): 359-366.
[7] Ghazijahani T G, Dizaji H S, Nozohor J, et al. Experiments on corrugated thin cylindrical shells under uniform external pressure[J]. Ocean Engineering,2015(106): 68-76.
[8] Ross C T F, Terry A, Little A P F. A design chart for the plastic collapse of corrugated cylinders under external pressure[J]. Ocean Engineering, 2001(28): 263-277.
[9] 中國船级社. 潜水系统和潜水器建造入级造规范[R].北京,2013.
China Classification Society (CCS). Rules for the classification and construction of diving systems and submersibles[R]. Beijing,2013.
