巧用“一题多解”渗透数学核心素养

李巧妮

【内容摘要】在高中数学教学的过程中，教师要注重培养学生的核心素养，讲授正确的学习方法，使得学生灵活地运用所学的知识做自主思考，而不是完全地依赖教师追求数学考试成绩的提高，在高中数学教学的过程中不能限制学生的思维方式，推行“一题多解”的方式提升学生的核心素养，有效提升高中的数学课堂教学质量。

【关键词】高中数学 一题多解 核心素养

核心素养的培养是当前高中数学教学的一项重要的目标，数学学科的核心素养包括了抽象思维、逻辑思维、预算能力以及数据分析能力，在教学优化的过程中，教师引导学生建立“一题多解”的思想，培养学生的核心素养，有助于高中生的综合素养提升。

一、在数学课堂上给予学生自主思考解题方法的空间

在高中数学教学的过程中，教师应当注重增强学生的主体地位，强调学生灵活地运用所学的知识进行自主思考，降低学生对于教师的依赖，主动进行问题的思考，探索数学问题的解答方式，夯实学生的知识学习能力。

在课堂上提出数学问题，教师先给予学生一定的时间和空间进行问题的自主思考，鼓励其提出多种解题的思路，在课堂内进行解题思路的分享，使得学生在数学课堂上的思维更加活跃，敢于发言。

例如：在研究题目“在三角形ABC中，D在BC上，AD平分角BAC，若AB=3，AC=1，∠BAC=60°，则AD是多少？”

在分析这道题目的时候，教师先让学生自主地进行思考，写出自己的解题思路，并在题目解答的时候写出题目中都涉及了哪些知识点的考核，经过教师的提醒，学生会先思考题目中考察的是哪些知识点，之后从知识点的梳理的角度研究题目的解题思路。现依照题目的条件画出几何图形（图1），标出已知条件，为后续的解题打下基础：

通过已知条件，學生很容易就探究出几个几何图形之间的关系：BC=AB+AC2-2AB·AC·cos∠BAC=7，由此展开计算的过程，此方法学生很容易第一时间想到，但却需要花费大量的时间进行计算。从客观题的角度来说，高中生一道填空题所花费的时间较长，为了鼓励学生使用简便的方法解题，教师要继续引导学生探究简便的解题方法。

基于教师的提示，学生思考所本题涉及的考点，便是余弦定理，AD平分∠BAC，则可以得出ABAC=BDDC，得出BD和DC的数值，根据cosB=AB2+BC2-AC22AB·BC=527之后根据几何关系AD2=AB2+BD2-2AB·BD·cosB=2716，最终可以得出本题的正确答案。这一解法在思路梳理的时候应用的余弦定理的相关知识，避免了复杂的计算步骤出现，引导高中生思考余弦定理的深度含义，这一解法锻炼了学生的抽象思维能力，使得学生的解题效率提升，解题的正确率也大大提高。

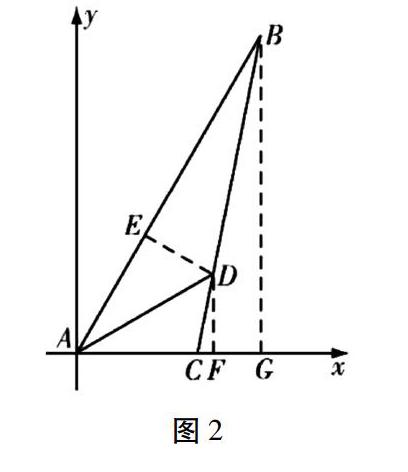
学生在研究的时候还提出了另一种解法。在几何图形内辅助使用直角坐标系的方式将题目的已知条件清晰地呈现在坐标系内，使用多条辅助线以及直角坐标的方式理清解题的思路。如图2所示：

A点作为直角坐标系的原点，AC在X轴上，C点的坐标为（1，0），B点的坐标为（32，332），过D点做到X轴的垂线交点为F，同时作AB的垂线交点于E，过点B作X轴的垂线，交于点G。之后学生可以借助直角三角形的方式完成后续的解题。在几何图形中建立直角坐标系，利用垂线以及平行线的方式拓宽解题的思路，让学生节约解题的时间，减少计算的繁琐步骤，使得学生将坐标知识与几何知识联系在一起，增强理论联系实际的能力。

一道题目学生可以从考察知识点的方式梳理解题的思路，活跃高中生的思维，让其可以从现有的知识框架中灵活调动，让学生独立思考，成为课堂的主人，不再完全依靠教师的讲解，而是养成良好的学习习惯，有助于提升学生的学科核心素养。

在引导学生建立“一题多解”的思路的时候，教师引导学生从多个角度进行问题的深度挖掘，将所学的知识与不同的题型联系在一起，建立一个整体解题观念，而不再是就题目而解答题目。基于这样的培养过程，教师可以辅助学生形成优化的认知结构，联系不同领域的数学知识，提升自我的核心素养，养成良好的自主学习习惯。

高中数学教师在课堂教学的时候为学生引入多种的学习思路，讲方法，重机技巧训练，使得学生建立良好的思维意识，正确认识数学学科的内涵，让其可以体会和认识数学学科的内涵，灵活地思考日常遇到的数学问题，给予学生更多的机会独立思考，提升高中生的问题解答的能力。

高中的数学教师要正确疏导高中生承担的压力，深入到学生的内心世界进行课堂的优化以及设计，减缓学生承担的压力，不能将数学考试当作唯一的学习目标，而是以提升学生的核心素养作为终极的教学目标，创新课堂的教学形式，吸引学生的注意力，让高中生享受数学学习的乐趣，而不是将其当作既定的任务，由此引导高中生正确认识数学学科，真正地喜爱数学学科，养成良好的自主学习习惯，提升自我的综合能力为今后的学习以及进步奠定良好的基础。

二、运用变式教学培养学生勇于探究的精神

在一题多解思维培养的过程中，教师最重要的是要激发学生的兴趣，让学生在自主研究的过程中产生兴趣，逐渐感受到数学解题方法的多样性以及多变性，在自主课堂中，教师运用数学解题方法的变式研究学生体会解决数学问题的成就感，增强学生运用知识以及探究知识的兴趣以及勇气。

例如：在解答问题“方程组

有两个不相等的根，求取a的取值范围是？”的时候，教师鼓励学生提出不同的解题思路，其中一个同学提出将方程组②代入到方程组①中变化成为一个一元二次方程，再利用根的判别式求出a的范围。另一个同学提出“将代数问题几何化”的思想，将原有的方程组转化为两个几何圆形之间的位置关系，当两个圆的位置是相交的关系的时候，可得两圆圆心之间的距离d=（2a-0）2+（a+3-0）2=5a2+6a+9，由两圆相交可得2-1<5a2+6a+9<2+1，平方可得1<5a2+6a+9<9，进而可以计算出a的取值范围：-65

教师在指导变式求解的时候，要对学生提出的新颖的解题方法进行表扬与肯定，尤其是第二名同学的解题思路与方法，将代数问题巧妙地进行化解，转化为常规的几何位置判定的解题方式，转变解题的思路，化繁为简。在自主研究的过程中，教师可以鼓励学生多方位地思考，将不同模块的知识联系在一起，增强学生知识掌握程度的同时，让学生在不断攻克难题的过程中产生自信心。通过这一道题目的讲解与分析，教师可以很好地为高中生引进数形结合的思想，让学生体会和思考不同数学问题之间相同的思维方式和解题脉络，力求引导高中生将数学问题和数学知识做到融会贯通，掌握一种方式，进而可以在面对复杂的数学问题的时候找到解题的思路，一题多解的时候找寻效率最高、计算最少以及步骤最简便的方式，不仅有助于高中生提升考试的正确率，还可以让高中生不断积累数学自信心，养成勇于探索以及思考的精神，不会过度依赖教师，积极主动地寻求解题的方式，让高中生的数学学习核心素养得到提升和进步。

三、总结

在一题多解思维的培养下，教师不仅让学生成为课堂的主导，更多的是让学生掌握数学思考的方式，对问题的不断反思以及对知识的深度挖掘，对于高中生的思维能力和思维水平的提升有很大的帮助，在课堂讲解例题的过程中，教师重视学生的思维过程，让学生多角度探索解题方式，给学生更完整的数学学习的体验，对高中生的核心素养提升有非常积极的帮助。

【参考文献】

[1] 刘金铭. 论高中数学一题多解与学生核心素养的提升[J]. 高考， 2019（17）：203.

[2] 刘彦永. 巧用“一题多解”渗透数学核心素养[J]. 中小学数学：高中版， 2017.

（作者单位：甘肃省临夏中学）