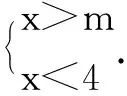数形配口诀 学懂不费力

周天喜

(江苏高邮市城北中学 225600)

笔者在一元一次不等式组教学中，发现学生因面对已知不等式组有解无解或有几个整数解，需确定待定字母的取值范围时而感到困惑，不可理解，极易出错.面临这种现象，笔者运用数形结合画出数轴，配上通俗易懂的口诀解说词，这样就突破学生理解上的瓶颈，从而提高课堂学习的有效性.

一、已知不等式组有解无解，确定待定字母的取值范围

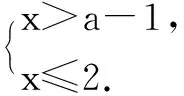
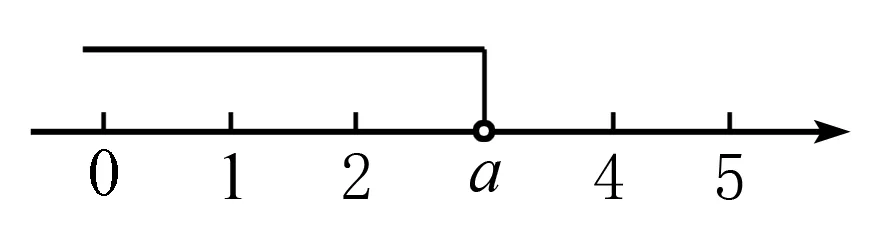
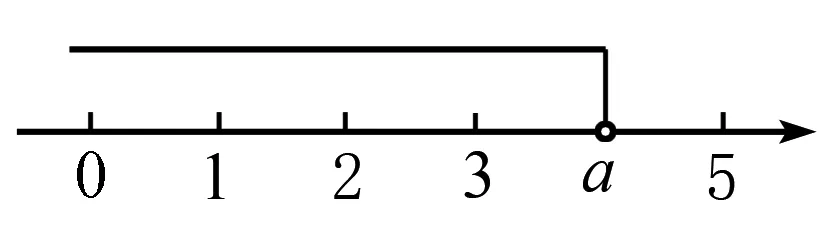
在数轴上表示出解集x≤2,表示数(a-1)的点的位置可分三种情况：①数2的点的左边；②数2的点处；③数2的点的右边，简称左、上、右.

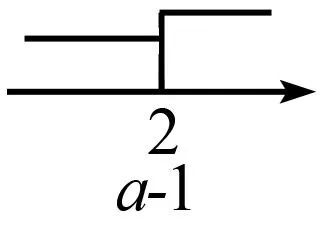
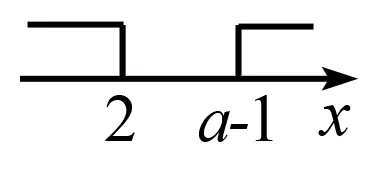
综上所述：a-1<2,解得a<3.

数学口诀：画出左上右，秒杀不出错.

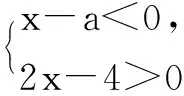
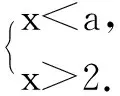
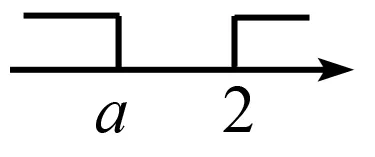
综上所述：a≤2.

二、已知不等式组的整数解的个数，确定待定字母的取值范围

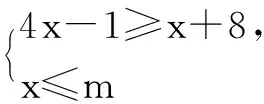
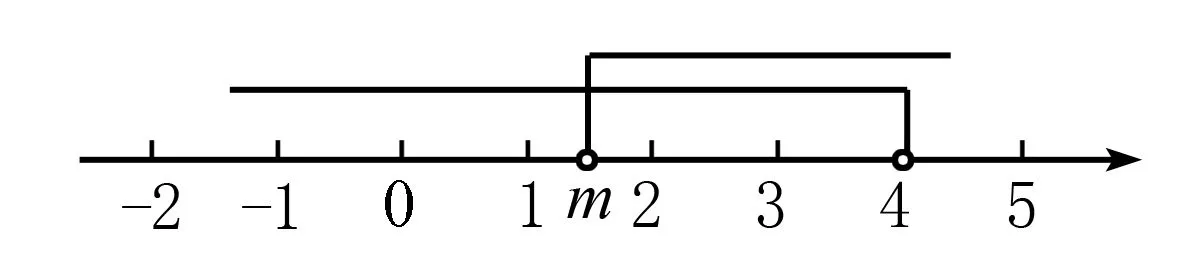
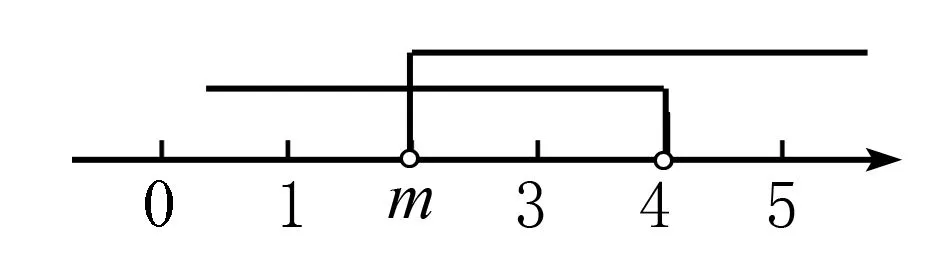
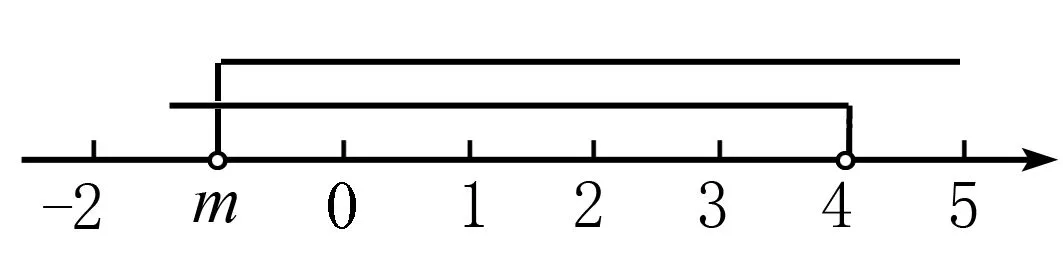
在数轴上表示出解集x≥3，因不等式组有3个整数解，所以表示数m的点的位置应画在整数点5和整数点6之间，简称“画中间”.

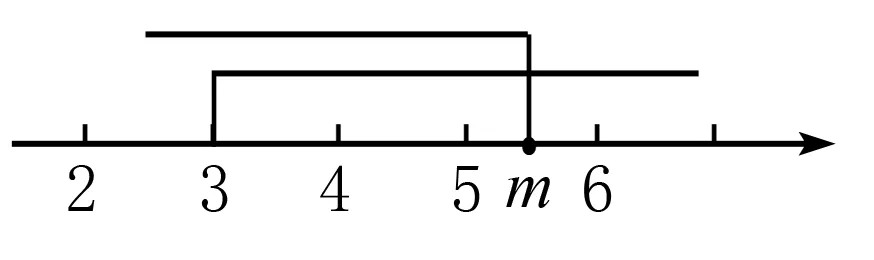
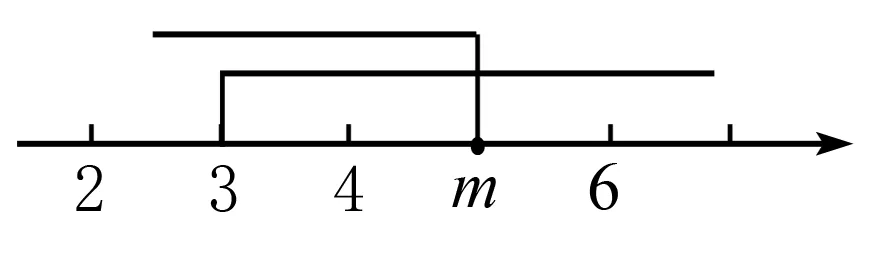
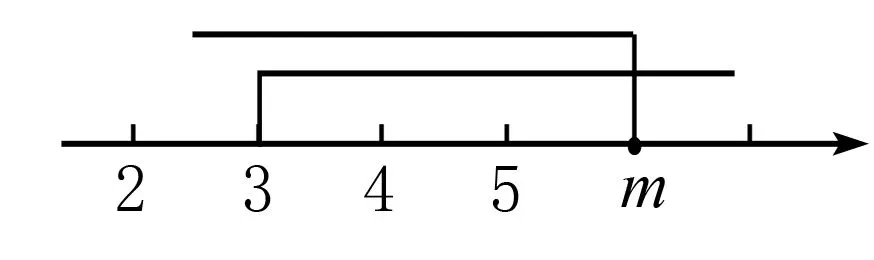
综上所述：5≤m<6.

数学口诀：画中间，验两头.

例4若关于x的不等式x-a<0的正整数解共有3个，求a的取值范围.

解析原不等式解集可化为x

综上所述：3

0、1、2、3，成立.

整数-1、0、1、2、3，成立.

整数0、1、2、3，不成立.

综上所述：1≤m<2或-2≤m<-1.

针对以上两种题型，运用数形配口诀的解题策略，能收到深入浅出、直观生动、事半功效的教学效果.事实证明，学生掌握了这种方法，能极大地提高解题的正确率，从而提高学习数学的有效性.