换元法在初中数学解题中的应用

赖振华

(福建省平和县文峰中学 363700)

在初中数学新课程标准中明确提出，初中数学的学习首要目标就要求学生在学习的过程中，获得必备的数学基础知识、数学基本技能等，并对最基本的数学概念、数学结论的本质等进行理解，进而充分体会初中数学中所蕴含的数学思想和数学方法等.因此，在初中数学教学中，必须要充分借助“换元法”以提升学生的解题效率.

一、换元法概述

换元法又称之为辅助元素法、变量代换法，主要是将某一个式子看做成一个整体，并用另一个变量去代替它.换元的实质就是转化，是用一种变数形式对另一种变数的形式进行取代，进而使得问题得到了有效的简化.可以说，在使用换元法这一方法对初中数学问题进行解答的时候，其关键就在于合适地选择出“新元”，并将其引入到数学问题中进行适当的代换，进而找到数学问题的解题思路.

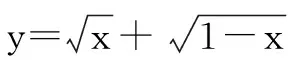
总而言之，在对数学问题进行解决的过程中，换元法是最为常用的数学解题方式.通过换元法的应用，使得整个数学运算更加简便，进一步提升了学生的解题效率.

二、换元法在初中数学解题中的具体应用

1.在因式分解中的应用

在初中数学知识体系中，多项式的因式分解历来是教学、考试的重点.就因式分解这一部分的内容来说，虽然总体难度不是特别大，但是涉及到的基础知识却非常多.例如：加减乘除、平方、代数式等，学生在进行该部分数学问题的解决过程中，必须要对因式分解与整式乘法之间的关系，并对新旧知识之间的比较进行探索，进而掌握因式分解的主要方法.

而在进行因式分解问题解答的过程中，换元法则是学生最为常用的方法，并深得学生的青睐.具体来说，换元法在因式分解中应用的时候，首先应将原代数式中的某个部分，用新元对其进行代替，以达到减少因式项数的目的，进而使得问题变得更加简单.

2.在解方程组问题中的应用

方程组也是初中数学中最为重要的内容，在对这部分数学问题进行解答的时候，学生只有明确找出未知条件、已知条件两者的关系，或者将方程组中所隐蔽的已知条件之间的关系进行明确的时候，才能将新知识进行转化，使其成为旧知识，进而对其进行有效的解决.而在这一过程中，则离不开换元法的应用.

3.在整式运算中的应用

在初中数学学习中，整式运算是学生最为常见的运算问题，同时整式运算也相对比较复杂.许多学生面对这一问题，常常无从下手，不知道如何对其进行解决.据此，教师在引导学生对其进行解答的时候，可充分借助换元法的形式，将相同的部分看做一个整体，并利用新元对其进行替代，进而这一复杂的问题进行转换，使其成为一个简单的数学问题.

例如，在对(1-2-3-…-998)(2+3+4+…+999)-(1-2-3-…-999)(2+3+4+…+998)这一整式进行运算的时候，就可以充分借助换元法，将(2+3+4+…+999)设置为a，将(2+3+4+…+998)设为b，那么该整式运算就会简化为(1-b)a-(1-a)b，进而使得整个整式运算更加简单.

综上所述，在初中数学学习中，学生经常会遇到比较复杂的数学问题，如果直接按照原始的方式对其进行求解，不仅使得数学问题变得十分棘手，并且致使学生在对数学问题进行解决的过程中，常常出现无从下手、频频出现错误等现象.因此，在指导学生对这些数学问题进行解决的过程中，就可以引导学生充分借助换元法的方式，将复杂的数学问题进行简化，进而促使学生对其进行顺利解决.