带攻击玩家的演化拥塞博弈的鲁棒性分析
2020-06-30王桂林
王桂林,徐 勇
(河北工业大学理学院,天津 300401)
0 引言
拥塞问题起源于交通工程,由于缺乏管理机构有效的集中调控,加之出行者的个人自主行为,目标在于最小化自己的花费,因此,采用博弈论来研究这类问题是十分必要的。Rosenthal首次提出拥塞博弈[1],并且指出拥塞博弈一定存在纳什均衡。基于其良好性质,生活中很多的拥塞问题均可采用拥塞博弈得以解决,比如交通网络问题[2]、认知无线电网络问题[3-4]、以及资源分配问题[5-6]等。
近年来,程代展教授提出矩阵的半张量积理论,为演化博弈论的研究提供了良好的工具。利用矩阵的半张量积理论,将演化博弈建模成逻辑动态系统,并将其表示成代数形式,通过分析状态转移矩阵的结构来分析玩家的策略行为。在此基础上,已有学者研究了演化博弈的稳定性与镇定性[7]、公共物品演化博弈的策略最优[8]等理论。在生物系统和经济行为中,因玩家数目庞大,故玩家只与其邻居玩家进行博弈,此博弈可用网络拓扑图直观表示玩家之间的关系,诸多学者在网络演化博弈的领域得到了许多理论结果。比如,网络演化博弈的分析控制[9]、带时滞的网络演化博弈的控制[10-11]、以及网络演化博弈的策略一致性[12]等。拥塞博弈也可以被重复进行,称之为演化拥塞博弈。文献[13]研究了演化拥塞博弈的收敛速度,证明演化拥塞博弈的纳什均衡点是不动点。文献[14]利用矩阵的半张量积将经典拥塞博弈表示成代数形式,针对动态设备系统,通过优化每个玩家的支付函数来实现全局最优,得到玩家采用串联型短视最优响应更新规则的演化动态一定会全局收敛到纳什均衡。另外,矩阵的半张量积理论在布尔(控制)网络的应用也十分广泛,得到了布尔(控制)网络的集控性[15]、能观性[16]、稳定性[17]、以及切换布尔网络的镇定性[18]等理论。
在社会网络中,玩家在进行演化博弈时可能会存在攻击玩家干扰其他正常玩家的策略选择,该攻击玩家可能会不考虑其他玩家的利益。此时,随之而来的问题就是如何保证其他正常玩家的利益。所以,在演化博弈中,可以施加鲁棒控制器来影响博弈的演化过程,从而使得系统中的可行状态能收敛到纳什均衡[19]。因为在系统中,可能会存在一些不合理的策略局势,比如,文献[20]图1的棋盘中,根据象棋的规则,局势C2→B3是不可行的。在布尔网络[21-22]、网络演化博弈[23]等领域的鲁棒性问题都已被研究,但是在演化拥塞博弈领域还没有相关的研究文献。
本文利用矩阵的半张量积方法,考虑带有攻击玩家和可行状态受限集的拥塞博弈演化过程鲁棒性问题。由于在实际的拥塞问题中,所有玩家在下一时刻都可能进行策略更新,所以本文采用并联型短视最优响应策略更新规则。然而对于可行状态受限集中的所有初始状态,要使得带有攻击玩家的演化拥塞博弈直接鲁棒可达纳什均衡是不容易的,为此,通过施加鲁棒控制器来影响博弈进程是非常必要的。本文通过设计开环控制和状态反馈控制,使得带有攻击玩家的演化拥塞博弈中的可行状态受限集中的所有初始状态鲁棒可达纳什均衡。本文的主要贡献如下:1)将半张量积的方法应用于带攻击玩家和可行状态受限集的演化拥塞博弈的研究;2)给出了设计控制的方法,使带攻击玩家的演化拥塞博弈中的可行状态受限集中的所有初始状态鲁棒可达纳什均衡。
1 预备知识
首先定义一些概念:

2)Dk:={1,2,…,k},k≥2。
4)Col(A)表示矩阵A的列的集合,Coli(A)表示矩阵A的第i列。
5)Lm×n表示m×n维逻辑矩阵的集合,L=δk[i1,i2,…,in]是结构矩阵。
6)A和B的布尔乘积可定义为A×BB=(aij×Bbij)=(aij)∧(bij)。
然后介绍一些关于半张量积以及博弈论的定义及性质。
定义1[7]矩阵Am×n和矩阵Bp×q的半张量积是

其中,t是n和p的最小公倍数,⊗表示Kronecker积。
定义2[24]矩阵Ap×n和Bq×n的Khatri-Rao积为

性质1[24](伪交换性) 设X∈Rp是一列向量,B为任意矩阵,那么

性质2[24]设X∈Rm,Y∈Rn是两个列向量,那么
W[m,n]XY=YX
其中,W[m,n]=δmn[1,m+1,…,(n-1)m+1,2,m+2,…,(n-1)m+2,…,m,2m,…,nm]为换位矩阵。
性质3[24]设X∈Δk,那么
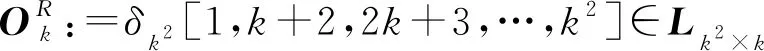
引理1[24]令f(x1,x2,…,xn):Dn→D是逻辑变量x1,x2,…,xn的逻辑函数,则

其中,Mf是f的结构矩阵。

2 主要结果
本节首先给出经典的拥塞博弈;然后建模演化拥塞博弈的动态系统,并将其表示成代数形式;最后建模带攻击玩家和控制玩家的演化拥塞博弈的动态系统,设计开环控制和状态反馈控制,使得带攻击玩家和可行状态受限集的演化拥塞博弈鲁棒可达纳什均衡。
2.1 拥塞博弈
一个拥塞博弈G=(N,P,(Si)i∈N,(Ξj)j∈P),其中
1)N={1,2,…,n}表示玩家集;
2)P={1,2,…,p}表示资源集;
3)Si⊂P表示玩家i的策略集,其中si∈Si是i的策略;

令所有资源的花费函数为
Ξ=[Ξ1,Ξ2,…,Ξp]
(1)
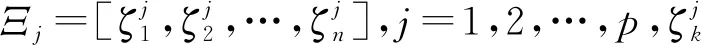
则玩家i的花费函数为
2.2 演化拥塞博弈的动态系统及代数形式
首先给出演化拥塞博弈的动态方程
xi(t+1)=fi(x1(t),x2(t),…,xn(t)),i=1,2,…,n
(2)

本文采取的策略更新规则是并联型短视最优响应。最优响应集
则玩家i在时刻t+1的策略选择为
(3)
然后将演化拥塞博弈的动态系统(2)表示成代数形式
xi(t+1)=Mix(t),i=1,2,…,n
(4)
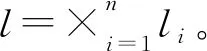
将系统(4)中的方程整合得到
x(t+1)=Mx(t)
其中,M=M1*M2*…*Mn∈Ll×l,“*”是Khatri-Rao积。
注1:文献[13]已证明演化拥塞博弈至少有一个纳什均衡点。
2.3 带攻击玩家和可行状态受限集的演化拥塞博弈的鲁棒性分析
这一部分主要考虑通过添加控制玩家来研究带攻击玩家和可行状态受限集的演化拥塞博弈的鲁棒性。不失一般性,假设玩家1,玩家2,…,玩家q是攻击玩家,玩家q+1,玩家q+2,…,玩家m是控制玩家,其他n-m个玩家是正常玩家。
根据式(2),带攻击玩家和控制玩家的演化拥塞博弈动态方程为
xi(t+1)=fi(ξ1(t),…,ξq(t),uq+1(t),…,um(t),xm+1(t),…,xn(t)),i=m+1,…,n
(5)
将(5)转化成代数形式并相乘得
z(t+1)=Lξ(t)u(t)z(t)
(6)

假设正常玩家的策略局势集都取自于可行状态受限集:
(7)
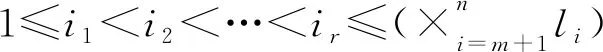
下面介绍带有攻击玩家和可行状态受限集的演化拥塞博弈鲁棒可达纳什均衡的定义。记纳什均衡点集Ω。

定义4带有攻击玩家和可行状态受限集Γz的演化拥塞博弈鲁棒可达纳什均衡,如果对于任意的初始状态z(0)∈Γz,在任意ξ(t)下,存在控制u(t),使得

接下来,设计开环控制和状态反馈控制,使得系统(6)Γz中的所有状态鲁棒可达纳什均衡。
先考虑开环控制,给出定理1。
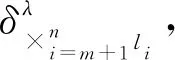
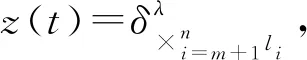
接下来设计状态反馈控制,形式如式(8):
(8)
假设gi的结构矩阵是Ki,i=q+1,q+2,…,m,则状态反馈控制式(8)可表示成代数形式
u(t)=Kz(t)

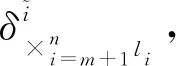
将(6)变为

(9)





定理2系统(9)Γz中的所有状态能够通过状态反馈控制鲁棒可达纳什均衡,当且仅当存在一个整数σ满足1≤σ (10) 证明:(充分性)假设式(10)成立,在任意的ξ(t)下,通过构建状态反馈控制矩阵K使得系统(9)鲁棒可达纳什均衡。 (11) (必要性)假设系统(9)Γz中的所有状态能够通过状态反馈控制u(t)=Kz(t)鲁棒可达纳什均衡,则系统(9)和控制u(t)=Kz(t)变成 (12) 注2:状态反馈控制的设计重点在于增益矩阵K的设计。设计过程为 考虑4个玩家N={1,2,3,4},5个资源P={1,2,3,4,5}组成的拥塞博弈。4个玩家的策略集 由式(1),设所有资源的花费为 Ξ=[2,3,5,7,3,5,6,9,2,4,6,10,3,6,7,8,2,5,7,9] 根据策略更新规则(3),拥塞博弈的演化动态的代数形式表示为 x(t+1)=Mx(t) 其中,M=δ54[45,24,18,53,14,26,27,24,27,15,24,15,23,14,23,24,24,24,18,24,18,26,14,26,27,24,27,45,24,18,15,45,18,9,6,9,15,24,15,15,15,15,6,6,6,18,24,15,17,14,14,9,6,6],x(t)=x1(t)x2(t)x3(t)x4(t)。 现在考虑带有攻击玩家的演化拥塞博弈。在演化拥塞博弈中,假设玩家1是攻击玩家,玩家2是控制玩家,玩家3和玩家4是正常玩家。令ξ(t)=x1(t),u(t)=x2(t),z(t)=x3(t)x4(t)。得到带攻击玩家的演化拥塞博弈的代数形式 z(t+1)=Lξ(t)u(t)z(t) (13) 其中,L=δ9[9,6,9,8,5,8,9,6,9,6,6,6,5,5,5,6,6,6,9,6,9,8,5,8,9,6,9,9,6,9,9,6,9,9,6,9,6,6,6,6,6,6,6,6,6,9,6,6,8,5,5,9,6,6]。 接下来设计状态反馈控制u(t)=Kz(t),K=δ3[α1,α2,α3,α4,α5,α6,α7,α8,α9],使得带攻击玩家和可行状态受限集的演化拥塞博弈鲁棒可达纳什均衡。 将式(13)转换成 则有 R11=δ9[9,6,9],R32=δ9[9,6,0],R53=δ9[0,0,5],R74=δ9[9,6,9],R95=δ9[9,6,0] K=δ3[α1,α2,1,α4,3,α6,α7,α8,1] 图1 可行状态受限集Γz的鲁棒控制过程 本文研究带攻击玩家和可行状态受限集的演化拥塞博弈的鲁棒控制问题。首先,将带攻击玩家和控制玩家的演化拥塞博弈建模成多值逻辑动态系统,利用矩阵的半张量积,给出等价的代数形式。在此基础上,分析博弈的动态行为。然后,对于给定可行状态受限集的任意初始局势,给出了该博弈是否存在控制使得其鲁棒可达纳什均衡的充要条件,并给出了控制的具体设计过程。需要指出的是,在基于半张量积方法的的带攻击玩家的演化拥塞博弈中,仍然有一些问题有待研究。比如,在实际带攻击玩家的演化拥塞博弈中,在攻击玩家和正常玩家进行决策时,可能会记住过去不止一个时刻的决策行为,所以带有攻击玩家的时滞演化拥塞博弈有待进一步研究。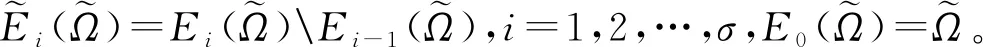





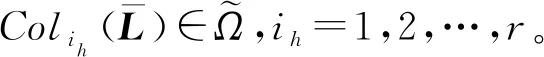

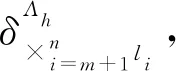
3 算例分析

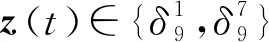





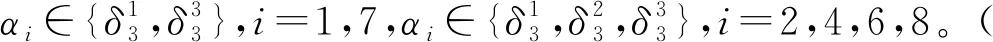

4 结论
