转向架钢弹簧表面磨痕深度对其寿命的影响研究

邓学晖，王 靖

(中车长春轨道客车股份有限公司，吉林 长春 130062)

0 引言

转向架钢弹簧是动车组的关键部件，在保证列车的安全运行中发挥着重要作用。在使用过程中，由于弹簧异常磨损和磕碰，会引起接触线磨损、表面磨损、表面磕碰等表面缺陷。由于弹簧一直处于高强度的交变载荷的作用，随着动车组列车运营里程的不断增加，磨痕深度会随之增加，因此校核转向架钢弹簧在不同深度磨痕下的疲劳寿命十分有必要。本文针对2种典型的磨痕形式，选取了不同磨痕深度的转向架钢弹簧，通过有限元仿真的方法对其进行疲劳分析，评估其理论工作寿命；并加工同等磨痕深度的转向架钢弹簧进行试验，对其实际工作寿命进行验证。

1 有限元理论计算基础

转向架钢弹簧在实际运营中受交变载荷作用，为方便分析，本文采用工程中广泛应用的Miner理论[1]，对钢弹簧的疲劳寿命进行估算。Miner理论是线性疲劳累积损伤理论，该理论认为，循环载荷可对材料产生损伤，且每次循环载荷对材料产生的损伤相互独立，且这种损伤可不断累加使材料发生疲劳破坏。材料的损伤程度与循环应力作用次数成正相关。载荷可分为i级循环应力，则不同级别的应力损伤相互独立，将各级应力损伤进行叠加可得材料总损伤，若损伤超过额定限度则材料开始发生破坏。

在Miner理论的基础上，采用名义应力法[2-3]的疲劳分析方法，对钢弹簧进行分析。名义应力法是在材料或者零部件名义应力和集中系数的基础上，利用零部件S-N曲线和疲劳累积损伤理论进行疲劳寿命计算的方法。名义应力法适用于高周疲劳，且零部件的变形处在弹性范围内的疲劳分析。

本文采用常见的估算材料疲劳极限的经验模型，即Goodman直线模型：

(1)

σa为材料所受循环载荷的应力幅值；σm为循环载荷的平均应力值；σ-1为在应力比为-1循环载荷时材料的疲劳极限；σb为材料的强度极限。

对于本文的弹簧模型，整体承受单向的垂向变化载荷，而弹簧截面为螺旋线上升，故实际截面上为剪切受力为主，因此在疲劳分析中σ取剪切应力shear stress。

2 有限元模型及仿真分析

2.1 模型结构说明

据实际需求，研究对象确定为CRH380BL高速动车组转向架钢弹簧。钢弹簧材料为51CrV4，钢弹簧主要结构尺寸如表1所示。

表1 螺旋弹簧基本参数

对于转向架钢弹簧的表面磨痕，内簧磨痕主要为外侧斜切式磨痕，属于表面磨损，主要是由于弹簧在使用过程中存在振动、横向作用力等因素使其与周围金属发生接触而导致的，一般出现在内簧的第2圈外侧上。外簧磨痕主要为接触线磨痕，主要出现在支撑圈与工作圈之间，由于支撑圈与工作圈的间距要小于工作圈间距，使其在冲击力情况下出现异常磨损。2种磨痕位置及尺寸如图1所示。

图1 内/外簧磨痕位置及尺寸说明

实际检修中发现，弹簧磨痕深度一般在0.2～0.5 mm之间。为进一步研究钢弹簧可接受的磨痕深度，本文拟分析更大磨损深度的钢弹簧。综上，选取如表2所示的不同磨痕深度的弹簧模型进行有限元分析，建立磨损弹簧有限元模型，添加材料特性参数及弹簧载荷边界条件，计算弹簧的疲劳寿命[4]。

表2 磨损钢弹簧模型 mm

2.2 有限元模型

本文分析的弹簧有限元模型分为原始模型和磨损弹簧模型。原始模型由外簧、内簧、顶部加载圆盘组成，采用四面体单元划分，弹簧单元平均尺寸为3.0 mm，顶部加载圆盘单元尺寸由3.0 mm过渡到15.0 mm。磨损弹簧模型在原始模型基础上，在磨痕位置做了网格加密处理，磨痕处网格平均尺寸为1.5 mm。有限元模型如图2和图3所示。

图2 原始弹簧模型

图3 磨痕处网格加密

2.3 弹簧材料特性

弹簧材料特性如表3所示。

表3 弹簧的材料特性

2.4 弹簧载荷边界说明

根据试验状态，对弹簧模型采用垂向加载，约束弹簧底端，顶端加载对应载荷。载荷大小根据标准取值[3]，对于垂向静载荷Fj，外簧取47 133 N，内簧取27 668 N，合力74 801 N；k为动载系数，拟取为0.3；加载频率根据情况取1 Hz。载荷加载示意如图4所示。

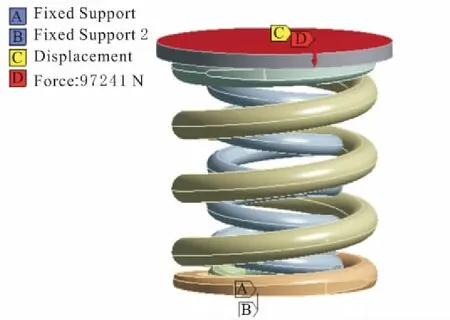
图4 载荷加载示意

2.5 仿真结果

建立磨损弹簧的有限元模型并进行静力和疲劳计算，得到如图5～图10所示的仿真结果。

观察图5剪切应力曲线，可以看到当磨痕深度较小时，内簧受到的剪切应力与无磨损状态差别不大。磨痕深度小于等于4.0 mm时(篇幅限制，只给出4.0 mm应力云图)，剪切应力与疲劳均无明显变化；磨痕深度大于4.0 mm时，剪切应力明显增大，且最大应力位置由第2圈内侧转移到磨痕处对应的内侧。此时最小疲劳寿命位置也由第2圈内侧转移到磨痕面附近。寿命位置转移之后，随着磨痕深度的增加，疲劳寿命大大减小。

观察图8剪切应力曲线，可以看到外簧磨痕深度较小时，外簧剪切应力与无磨损状态差别不大。磨痕深度大于1.2 mm时，最小疲劳寿命位置会发生转移，转移后弹簧疲劳寿命随着磨痕深度的增加明显减小；外簧磨痕深度大于3.0 mm时，受到的剪切应力明显增加，最大应力位置转移至磨损面附近。

图5 内簧仿真结果

图6 内簧磨损深度4.0 mm时最大应力点

图7 内簧磨损深度4.0 mm时寿命位置

图8 外簧仿真结果

图9 外簧磨损深度3.0 mm时最大应力点

图10 外簧磨损深度4.0 mm时最大应力点

3 试验验证

为了判断表面磨痕深度对钢弹簧剩余寿命的影响，本文以文献[5]为依据，对不同深度磨痕的钢弹簧进行疲劳试验，得到不同深度磨痕的钢弹簧的剩余可工作次数。试验中每隔20万次利用磁粉检测弹簧是否出现裂纹及断裂，如出现则判定钢弹簧失效，该组试验终止，如工作至合格标准次数仍未失效，则停止试验，认定该情况下钢弹簧仍满足合格标准[6]；本文中，在三级修弹簧(运营120万km)和四级修弹簧(运营240万km)的基础上，人为加工磨损深度，并施加文献[5]所述的载荷来进行试验。

3.1 试验设备

试验设备为西南交通大学大型转向架构架疲劳试验台，该系统由机械系统、液压系统、协调加载控制系统和通用测试系统组成。主要参数如表4所示。

表4 疲劳试验台部分作动器主要技术指标

3.2 试验结果

分析试验结果，得到如表5所示数据。

表5 弹簧实际剩余工作次数

对比弹簧实际剩余工作次数和仿真结果，剩余工作次数与磨痕深度的数据基本与仿真结果一致。

观察内簧(图11)断裂处和外簧(图12)断裂处发现，内簧裂纹是从磨痕最深处侧开始的，然后再逐步向钢弹簧线径内侧撕裂，最后断裂；外簧接触线断裂裂纹是从磨痕最深处侧开始的，然后再逐步向钢弹簧线径另一侧撕裂，最后断裂。断裂主要分为2个区域，分别为疲劳裂纹扩展区和瞬断区，即弹簧断裂模式属于疲劳断裂，断裂起源为弹簧受损处最深处表面，与仿真结果吻合。

图11 内簧断裂弹簧断口分析

图12 外簧断裂弹簧断口分析

4 结束语

本文中，仿真分析和试验结果基本吻合，分析磨痕深度对钢弹簧寿命的影响，主要规律如下：

a.当磨损深度在0.2～0.5 mm之间时，对钢弹簧薄弱节点平均应力和应力幅影响不大，因此单次载荷加载的疲劳损伤基本不变，使得内簧和外黄疲劳寿命基本不变。

b.对于内簧，磨损深度大于4.0 mm时，最大应力点会发生转移，由第2圈外侧转移到磨痕位置附近；最小疲劳寿命位置也转移到磨痕附近。对于外簧，磨损深度大于1.2 mm时，最小疲劳寿命位置会转移到磨痕位置附近；磨损深度大于3.0 mm时，最大应力点会发生转移。转移后弹簧的疲劳寿命随着磨损深度的增加而显著减少。究其原因，大的磨损深度下，单次载荷循环下的平均应力和应力幅增大明显，导致单次载荷加载的疲劳损伤越来越大，使得疲劳寿命越来越短。