基于改进小波阈值函数和变分模态分解的电能质量扰动检测

徐长宝，古庭赟，高云鹏，吴聪，龙秋风，周金

（1.贵州电网有限责任公司 电力科学研究院，贵州 贵阳 550001；2.湖南大学 电气与信息工程学院，湖南 长沙 410082）

电力系统非线性、冲击性、波动性负载的数量和容量不断增加，导致电网中出现大量谐波、电压暂降、短时中断等电能质量扰动问题，不仅严重危害电力系统和用电设备，导致数据丢失、设备误动作、生产流水线停机等系列问题，且容易给国家和企业带来不可弥补的经济损失.因此，深入研究影响电能质量下降的各种因素，对电能质量扰动问题进行准确检测与分析具有重要的现实意义[1-2].

现有特征提取分析方法已被应用于电能质量扰动检测领域[3-4].小波变换具有良好时频局部化特性，适合于暂态电能质量扰动检测，但其检测结果易受噪声影响，且分解效果取决基函数的选择和分解尺度[5].S 变换相比小波变换，抗噪性明显提高，但其窗函数缺乏灵活性，检测电压暂降和短时中断时效果不理想[6].原子分解具有优秀信号分解和重构能力，但暂态扰动检测计算量大、运算时间长[7].经验模态分解（Empirical Mode Decomposition，EMD）不需选取基函数，具有完全自适应性，适合于处理突变信号.集合经验模态分解（Ensemble Empirical Mode Decomposition，EEMD）在检测分析电能质量扰动信号时有较强的自适应性，但EMD 和EEMD 得到的固有模态函数易出现模态混叠和端点效应[8]，不利于扰动特征的准确提取.

变分模态分解算法（Variational Mode Decomposition，VMD）是由Dragomiretskiy 等[9]提出的一种利用变分思想进行信号分解的时频分析方法，通过变分框架准确求出非平稳信号的各本征模态函数，不仅具有抗模态混叠能力和噪声鲁棒性，还可有效提高分解效率.文献[10]分别研究变分模态分解在稳态电能质量扰动、暂态电能质量扰动中算法的适用性，不仅能准确提取振幅、频率等特征信息，且在处理复合扰动和频率相近的奇数次谐波时检测效果良好.文献[11]采用VMD 将电能质量扰动信号分解为系列调幅-调频函数之和，分别求解每个调幅-调频函数瞬时幅值和瞬时频率，相比经验模态分解和局部均值分解算法，不仅提取的扰动信号误差较小，且不存在模态混叠现象.但文献[10]未讨论在噪声情况下算法的适用性，文献[11]所提算法在噪声强度为20 dB 时算法失效.

因此，为了在强噪声情况下实现对电能质量扰动信号的准确检测和分析，本文提出一种基于改进小波阈值函数和变分模态分解的电能质量扰动检测算法，首先通过改进小波阈值函数对噪声信号进行预处理，再利用VMD 分解将去噪后的扰动信号分解成一系列本征模态函数，采用希尔伯特变换提取信号振幅、频率等特征信息，并通过奇异值分解（Singular Value Decomposition，SVD）实现扰动发生起止点的精准检测，最后通过仿真实验与实测数据验证本文提出算法的有效性和准确性.

1 变分模态分解和小波阈值去噪

1.1 变分模态分解

VMD 是一种非递归自适应技术，与传统的递归分解方法经验模态分解相比，VMD 具有更强的抗模态混叠能力和抗噪能力[12-13]，其实质是将输入信号x分解成一系列有限带宽的模态，每个模态围绕一个中心频率脉动，分解过程中的中心频率的值将被确定，VMD 根据调制标准对模态进行重新定义.模态的表达式为：

式中：uk为调制解调信号；φk（t）为相位，是非递减函数；Ak为包络函数.包络函数Ak和瞬时频率ωk=的变化速度比φ（kt）的变换速度缓慢.

为估计各个模态的带宽，对每个模态函数进行Hilbert 变换，得到对应的单边频谱；通过指数调节将每个模态解调到各自对应估计的中心频率，将获得的单边频谱转换到基带；对调制后的信号进行高斯平滑估计，即梯度的平方L2，据此估计每个模态的带宽.所定义的约束变分模型为：

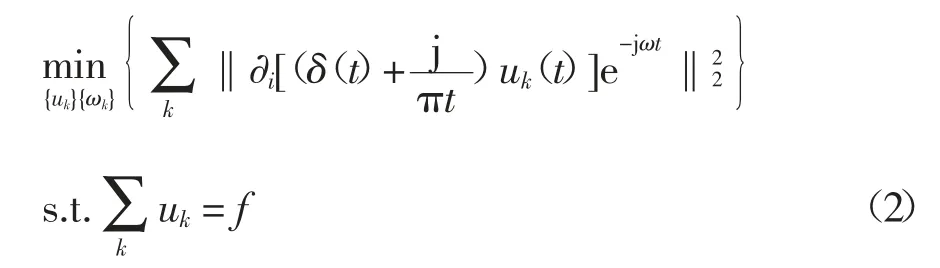
式中：uk为k 个模态；ωk为每个模态所对应的中心频率.为了使式（2）的变分问题不受约束，引入拉格朗日算子和二次惩罚因子将约束性变分问题转化成非约束性变分问题，其表达式为：

式中：α 为二次惩罚因子；λ 为拉格朗日算子.采用乘法算子交替方向法求取式（3）的最优解，即通过采用乘法算子交替方向法（Alternating Direction of Method of Multipliers，ADMM）求取式（3）的最优解交替更新寻找拉格朗日表达式的“鞍点”.的表达式为：

利用Parseval/Plancherel 傅里叶等距变换将式（4）转换至频域，可得

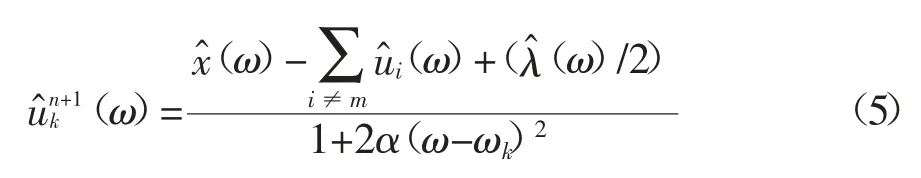
同理模态更新的推导过程，在傅里叶域中优化中心频率，求得中心频率的优化式为：

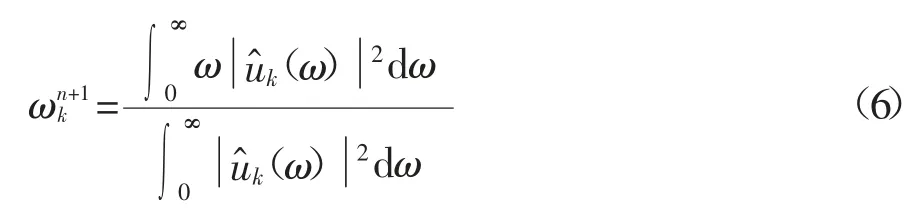
VMD 3 个参数需预先定义，预设尺度K、拉格朗日乘子更新参数τ 和惩罚因子α[14].对检测信号傅里叶谱分析可确定K 的大小；α 主要影响分解后各模态带宽以及收敛速度，且α 越大，各分量的带宽越小，反之则各分量带宽越大；α 取值过大或过小，VMD 计算耗时都会增加.因此本文综合考虑运行时间和各模态带宽两个因素，惩罚因子α 取2 000.τ 表征抗噪性，τ 越小，抗噪性越强，反之，则抗噪性能越弱，一般来说，τ 取0 或较小值的分解效果较好.

1.2 小波阈值去噪

电力系统中存在大量非线性负荷，实际采集的电能质量扰动信号常受噪声的污染，不利于对电能质量扰动信号突变点和频率幅值等特征信息的提取，只有有效滤除噪声，才能准确提取扰动特征.由文献[15]中提出的小波阈值去噪是一种有效的降噪处理方法，小波阈值降噪具体包括小波分解、阈值函数选取与阈值估计、一维电能质量扰动信号小波重构[16-17]，其具体步骤如下：

1）确定小波基和小波，对原始含噪信号Z（t）进行小波分解，得到各层小波系数wj，k；

2）确定阈值T 并使用阈值函数对小波系数wj，k进行处理，得到阈值处理后新的小波系数；

阈值和阈值函数的选取是小波阈值去噪方法的关键.不同的小波系数估计方法，对应于不同的小波阈值去噪方法，相应地形成硬、软阈值降噪方法.硬阈值函数的表达式为：

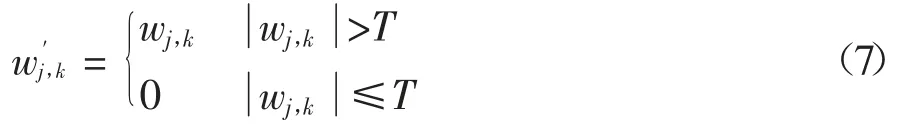
软阈值函数的表达式为：

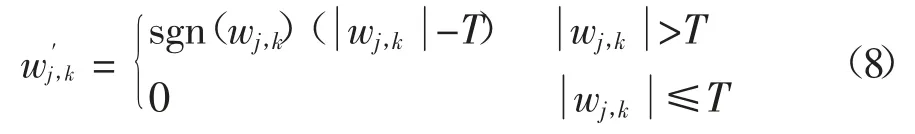
阈值T 估计的计算式为：

硬阈值和软阈值去噪方法虽得到广泛应用，但其本身有许多缺点，硬阈值函数得到的信号信噪比较高，但易产生信号局部振荡现象；而软阈值函数虽得到的信号较平滑，但信号信噪比较低，且得到的估计小波系数值与原小波系数存在固定偏差[6].

2 改进小波阈值函数和VMD 的扰动检测

由于传统的硬、软阈值函数对实际电网信号降噪处理过程的缺陷，本文提出改进小波阈值函数，该函数综合软硬阈值函数的优点，既具有连续性，又能很好地保留高频信息.其表达式为：

式中：a 为调节因子，可取任意正常数.当a→+∞时，改进小波阈值函数的极限趋近于wj，k-T，改进小波阈值函数等效于软阈值函数；当a 取任意正常数时，改进小波阈值函数极限趋向于T/2，使得阈值函数具有快速衰减和软阈值函数平滑的特点；当a 趋于0 时，改进小波阈值函数趋近于wj，k，阈值函数等效于硬阈值函数，因此通过调节a 的值可得到不同的阈值函数，使阈值函数分别具有硬阈值函数和软阈值函数的特点.图1 为改进小波阈值函数的示意图.

图1 改进小波阈值函数示意图Fig.1 Improved wavelet threshold function diagram

为了消除电能质量扰动信号噪声，同时较好地保留扰动信号的高频分量，实现准确检测扰动时刻，提取信号幅值、频率等特征信息，本文提出基于改进小波阈值函数和变分模态的电能质量扰动检测算法，其具体步骤如下：

步骤1 设输入的扰动检测信号为S（t），对其进行归一化处理.

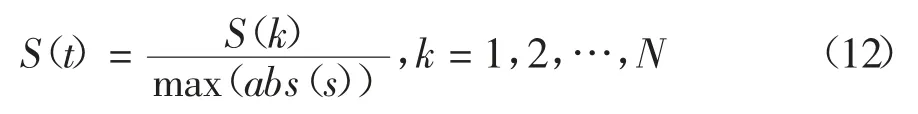
式中：k 为采样点；N 为采样点总数.

步骤2 选取sym8 小波基，设置分解层数为4，计算各层小波系数的噪声方差，再采用改进小波阈值函数对小波系数wj，k进行阈值处理，得到阈值处理后的小波系数

步骤4 将分解得到的每个ci（t）进行Hilbert 变换，得到

式中：di为第i 个ci（t）的Hilbert 变换；τ 为时间.由此可以构造解析信号.

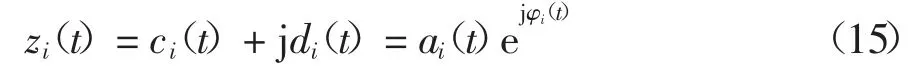
式中：

ai（t）为信号的瞬时幅值函数；φi（t）为相位函数.由相位函数进一步算出每个IMF 的瞬时频率为：

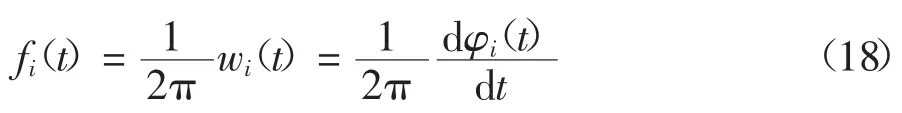
步骤5 根据瞬时幅值函数a（t）构造Hankel 矩阵，可得：

步骤6 对矩阵Q 进行四层线性分解，得到U=[u1，u2，…，um]，V=[v1，v2，…，vm]，可得

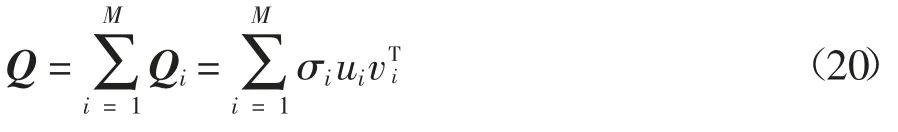
步骤7 依据每个矩阵Qi的第一行以及除去第一行元素的最后一列构造Pi向量，则

采用Pi分量中的突变信息来对电能质量扰动信号进行检测，本文选取P3实现电能质量扰动信号的检测.

3 仿真实验与分析

3.1 改进小波阈值函数与其他阈值函数对比

在电力系统中，常见的电能质量扰动信号包括电压暂降、电压暂升、短时中断、暂态振荡、谐波、暂态脉冲等.对电能质量扰动信号进行检测和分析前，需要针对信号的不同扰动类型，建立能够表征实际扰动信号典型特性的数学模型.表1 为上述6 种电能质量扰动信号模型S（t）.其中，T 为工频周期；u（t）为单位阶跃函数.

表1 电能质量基本扰动信号模型Tab.1 Basic disturbance signal model of power quality

为直观反映各类阈值函数降噪性能的优劣，将信噪比（Signal to Noise Ratio，SNR）和均方误差（Mean Square Error，MSE）作为评判降噪效果的依据[18-19].降噪信噪比越高，均方误差越小，则降噪效果越好.为进一步验证本文算法的准确性与抗噪性，分别采用本文的改进小波阈值函数、常用的软、硬函数以及EEMD 降噪、数学形态法滤除噪声对电能质量扰动信号S（t）进行降噪处理，其中原始信号的信噪比为20 dB.对比结果如表2 所示.

表2 不同降噪方法SNR 和MSE 对比结果Tab.2 Comparison of SNR and MSE results for different noise reduction methods

由表2 可知，数学形态法降噪后信号信噪比最低，滤波效果较差；EEMD 算法在脉冲、暂升以及暂降谐波中抗噪性能较好，但在振荡、暂降振荡中，检测效果较差且容易将高频有效分量滤除；软阈值函数对谐波信号的降噪效果较差，降噪后的信号容易丢失特征信息，影响去噪效果；硬阈值函数降噪总体降噪效果优于软阈值、EEMD 以及数学形态法，但在谐波检测中效果较差且重构信号所得的信号容易出现局部震荡，不利于信号进一步检测；改进小波阈值函数降噪方法无论在单一扰动信号还是复合信号扰动中，重构信号的信噪比和均方根误差的指标上相对于其他4 种降噪方法明显提高.实验结果表明，本文算法能有效去除干扰噪声，在提高信号信噪比的同时能最大还原原始不含噪信号，有利于信号的进一步检测.

3.2 单一扰动信号分析

在单一扰动信号检测仿真中，分别利用EMD、EEMD 和VMD 对同一扰动信号进行检测.电压暂降信号的表达式为：

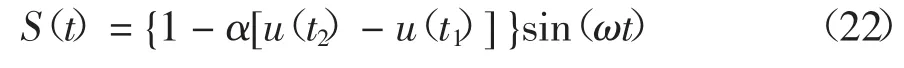
式中：ω=2πf，f=50 Hz，t2=0.14 s，t1=0.08 s，α=0.7 pu，采样频率为3 200 Hz，原始信号信噪比为20 dB，仿真时长为0.2 s.原始信号S（t）和降噪信号Z（t）的对比结果如图2（a）所示；图2（b）为信号Z（t）的傅里叶频谱图.由图2 可知，信号中仅存在50 Hz 的频率，因此分解个数K 的取值为1.

图2 单一扰动下改进小波阈值降噪信号及其傅里叶频谱图Fig.2 Improved wavelet threshold denoising signal and its Fourier spectrum under single disturbance

图3 分别为采用EMD、EEMD 和VMD 得到的瞬时幅值和瞬时频率图.通过对比可知，VMD 相比EMD 和EEMD 得到的幅值频率信息更准确，波动范围小，曲线更为平缓，能准确得到基波幅值为1 pu，频率为50 Hz，暂降深度为0.665 pu.EMD 和EEMD受噪声影响导致扰动信息提取不准确，EEMD 提取出的瞬时频率模态混叠现象严重，而EMD 提取的幅值、频率曲线波动大，检测误差较大.因此，在强噪声环境下，EMD 和EEMD 易受噪声的影响，在提取扰动特征信息时算法容易失效，而VMD 不但抗噪性能比EMD 和EEMD 好，且检测准确度更高.

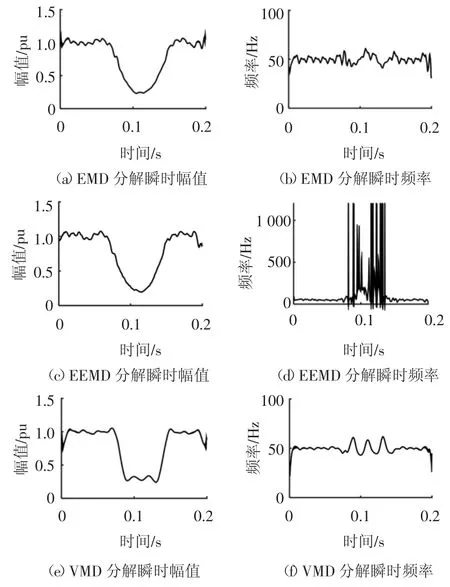
图3 单一扰动下EMD、EEMD 和VMD 幅频对比结果Fig.3 Amplitude-frequency comparison results of EMD，EEMD and VMD under single disturbance signal

图4 为采用奇异值分解算法进行阈值处理得到的暂降信号的扰动检测结果.由图4 可知，扰动发生的时刻为0.079 6 s，终止时刻为0.140 3 s.由上述结果分析可得，在噪声强度为20 dB 的强噪声环境下，本文所提算法不仅能准确提取出电压暂降信号的扰动幅值和时间等信息，且检测精度高.

为验证本文算法对不同类型扰动信号的检测性能，对表1 中5 种电能质量扰动信号添加信噪比20 dB 的高斯白噪声，分别采用EMD、EEMD 和VMD对其进行检测.检测结果如表3 所示.其中，C1 为暂降信号，C2 为暂升信号，C3 为电压中断信号，C4 为暂态脉冲信号，C5 为电压暂态振荡信号.

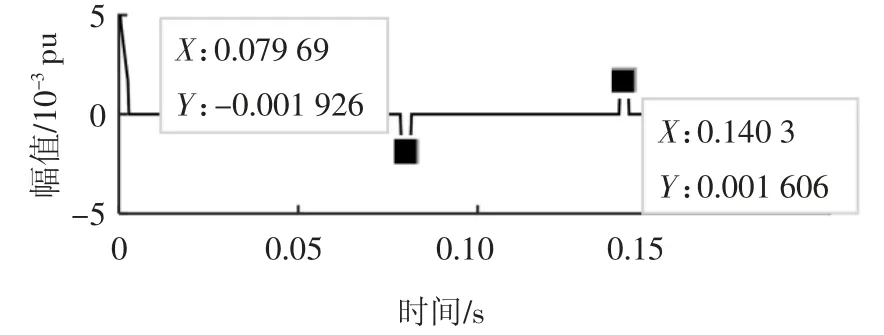
图4 电压暂降信号检测结果Fig.4 Voltage sag signal positioning result

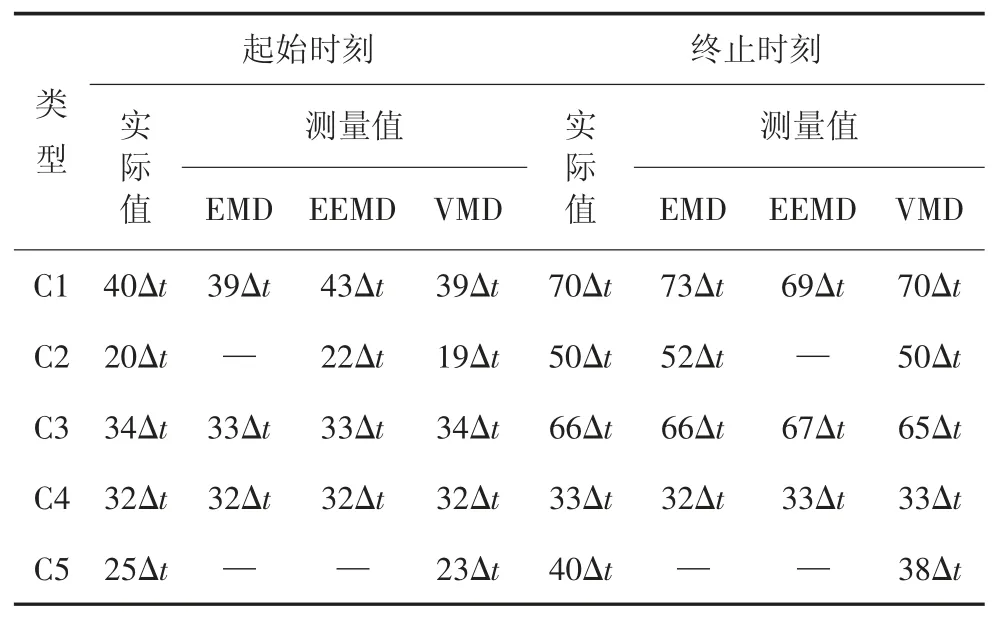
表3 不同类型扰动信号的起止时刻检测对比结果Tab.3 Starting and ending moment comparison results of different types of disturbance signals

由表3 可知，VMD 在3 种检测算法中的检测精度最高.EMD 方法的检测能力最差，抗噪性较弱.由于EMD 和EEMD 的模态混叠作用，导致两者在暂态振荡信号检测中检测失效.

由表4 可知，本文算法的检测效果优于EMD 和EEMD；VMD 对幅值和频率的检测精度要高于其他两类检测算法.对于脉冲信号，由于去噪算法会平滑掉一些幅值信息，所以EMD、EEMD 以及VMD 算法在扰动幅值检测上会有一定的误差.EMD 和EEMD在暂态振荡信号中已无法提取出电能质量扰动信息，但VMD 算法在振荡信号中仍然适用.结合表3和表4 可得，本文所提算法在单一扰动信号中的检测效果优于EMD 和EEMD，且检测准确度更高、抗噪能力更好.

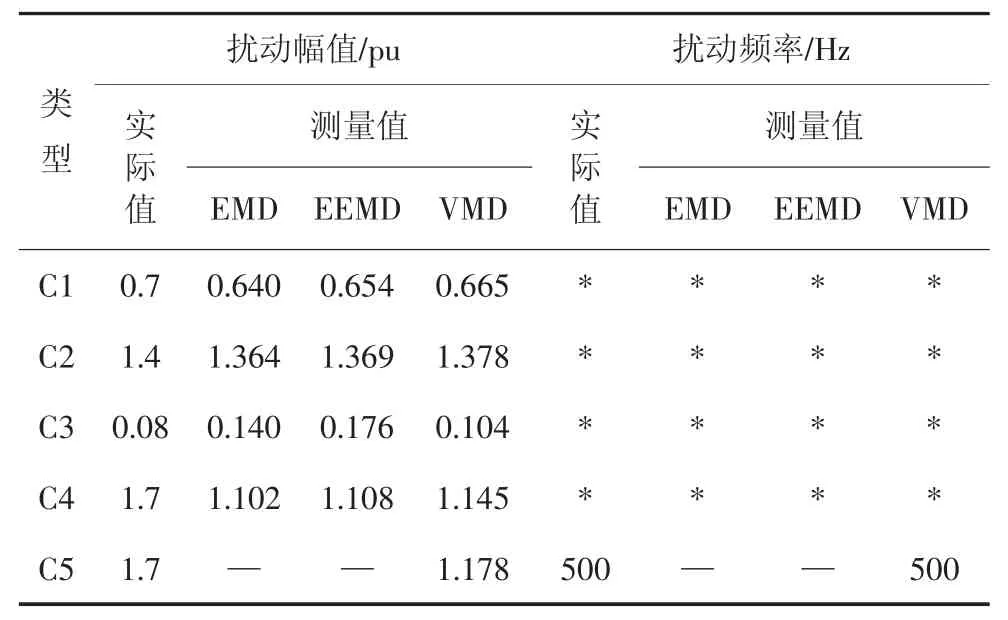
表4 不同类型扰动信号的幅值和频率检测对比结果Tab.4 Amplitude and frequency comparison results of different types of disturbance signals

3.3 复合扰动信号分析

复合扰动信号暂降谐波信号的数学模型为：

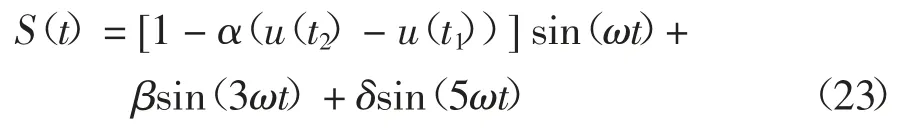
式中：ω=2πf，f=50 Hz，t2=0.14 s，t1=0.05 s，α=0.7 pu，β=0.35 pu，δ=0.2 pu，采样频率为3 200 Hz，原始信号的信噪比为20 dB，仿真时长为0.2 s.采用改进小波阈值函数降噪后的结果和信号傅里叶频谱图如图5 所示.由图5（b）可知，应用VMD 分析暂降谐波信号时K 设置3.

图5 复合扰动下改进小波阈值降噪信号及其傅里叶频谱图Fig.5 Improved wavelet threshold denoising signal and its Fourier spectrum under complex disturbance

图6 为利用VMD 算法分解得到的本征模态分量.由图6 可知，VMD 能准确地分离出基波、3 次谐波和5 次谐波且扰动细节保留完好.

图7 为采用EMD、EEMD 和VMD 分解后得到的复合扰动信号的幅频对比图.由图7 可知，VMD能有效地将信号分离出基波50 Hz、3 次谐波150 Hz和5 次谐波250 Hz.EMD 和EEMD 算法无法分离出不同频率的本征模态函数分量，模态混叠现象严重.VMD 分离出瞬时幅频曲线虽有一定幅度的波动，但特征信息明显.因此，在20 dB 强噪声情况下，对于复合扰动信号的检测，VMD 能正确分离出扰动分量，既没有因过分解产生的虚假分量也没有出现模态混叠现象，其检测效果同样优于EMD 和EEMD 算法.

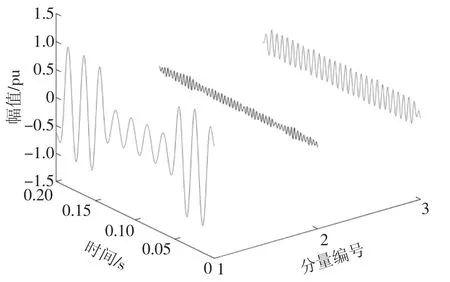
图6 VMD 分解得到的本征模态分量Fig.6 Intrinsic modal component obtained by VMD decomposition

图7 复合扰动下EMD、EEMD 和VMD 幅频对比结果Fig.7 Amplitude-frequency comparison results of EMD，EEMD and VMD under complex disturbance

图8 是暂降谐波信号定位检测结果图.由图8可知，暂降发生的时刻为0.050 3 s，终止时刻为0.139 4 s.为验证VMD 算法在复合扰动信号中的抗模态混叠能力和检测能力，本文还对暂降振荡复合信号进行检测，表5 为暂降谐波信号和暂降振荡信号的检测结果.其中，D1 信号为暂降谐波信号，D2为暂降振荡信号.

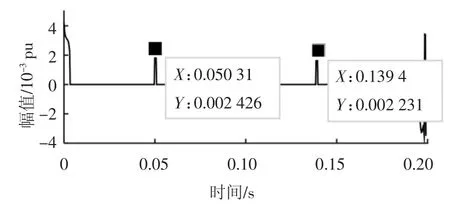
图8 暂降谐波信号定位检测结果Fig.8 Dumping harmonic signal positioning result

表5 不同类型复合扰动信号的检测对比结果Tab.5 Detection and comparison results of different types of composite disturbance signals

由表5 可知，在扰动检测方面，本文所提算法的检测结果与预设参数几乎无异；在扰动检测方面，由于暂降振荡信号中振荡信号的幅值呈指数递减，在降噪过程中会滤除掉一部分有效信息，造成扰动幅值的检测有一定的偏差，但仍能提取出明显的扰动信息.由上述结果可知，VMD 在强噪声条件下可实现复合扰动信号有效分析与检测，进一步验证了本文提出算法的准确性与有效性.

3.4 实际电网数据分析

采用IEEE 1159 监测电能质量网站上实时故障事件产生的电压信号，评估本文算法的有效性[20]，三相原始电压信号如图9 所示.扰动信号包括16 个正弦波周期，采样点数为256 个，信号频率为60 Hz.

图10（a）为实测信号的改进小波阈值函数降噪结果，图10（b）为实测信号的傅里叶频谱图.图10（a）中的信号幅值进行归一化处理.由图10（b）可知，实测信号进行VMD 分解时K 取1.

图11 为信号经Hilbert 变换得到的幅频分析结果.由图11 可得信号频率为60 Hz，基波幅值为0.815 3 pu，扰动幅值为0.321 7 pu，与FFT 分析结果一致.

图9 PQDiffractor 三相原始电压信号Fig.9 PQDiffractor three-phase original voltage signal

图10 电网实际扰动下改进小波阈值降噪信号及其傅里叶频谱图Fig.10 Improved wavelet threshold denoising signal and its Fourier spectrum under actual disturbance of power grid

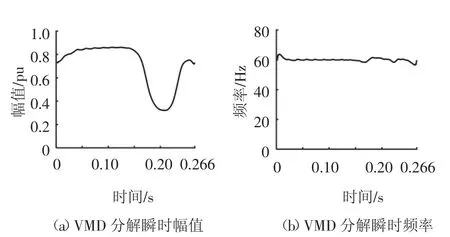
图11 电网实际扰动信号的幅频分析结果Fig.11 Amplitude and frequency analysis result under actual disturbance of power grid

图12 为实测信号的检测结果，扰动起始时刻为0.166 7 s，结束时刻为0.225 s.结合图11 和图12 可知，实测信号的扰动类型为电压暂降.综上所述，本文提出的算法对实际电网中非平稳信号具有很好的分析能力，能准确提取出扰动信息的时频特征，且可有效检测扰动的发生和恢复时刻.

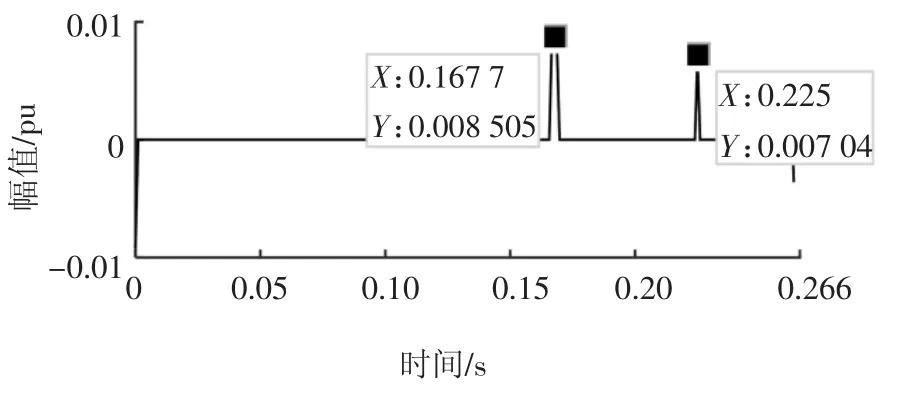
图12 电网实际扰动信号的定位检测结果Fig.12 Positioning result under actual disturbance of power grid

4 电能质量扰动检测平台

为模拟实际电网信号采集检测分析的过程，基于Agilent 33500B 函数发生器、PXIe-1071 机箱、PXIe-8840 控制器、NI PXIe-6341 数据采集卡、DSOX-2012B 示波器以及LabVIEW 上位机平台，开发了电能质量扰动检测平台.其中，PXIe-8840 控制器主频为2.7 GHz，具有多个USB 接口，可外接鼠标、键盘、显示器等设备，具有强大的运算能力.NI PXIe-6341数据采集卡具有16 位的ADC 分辨率、单通道以及多通道采样率，最大为500 kS/s，输入电压为±10 V.图13 为基于PXI 和LabVIEW 架构的电能质量扰动检测实验平台.

图13 基于PXI 和LabVIEW 架构的电能质量扰动检测平台Fig.13 Power quality disturbance detection platform based on PXI and LabVIEW architecture

由图13 可知，实际电网信号由函数信号发生器动态产生，通过示波器观察显示实测的电压波形，信号经PXI 高速数据采集卡电压模拟量输入通道实现数据采集，通过NI-DAQmx 进行通道数目、采样速率和输入范围等参数设置将数据实时传输至上位机，由上位机软件编程实现采集数据的实时波形显示、数据处理分析、检测分类识别、历史数据查询以及查询结果导出等功能.

5 结论

针对现有的电能质量检测算法抗噪性弱和检测精度不高的问题，本文提出了基于改进小波阈值函数和变分模态分解的电能质量扰动检测算法，将本文算法分别采用改进小波阈值与其他阈值函数对比、单一扰动、复合扰动仿真实验和实测信号的检测实验，结果表明，本文提出算法能准确提取信号的扰动起止时刻、幅值和频率等特征信息，且提取的特征值具有较高的精度；同时，对比EMD 和EEMD 的检测效果，证明了本文算法在抗模态混叠、抗虚假分量和噪声鲁棒性方面的优势；最终通过搭建基于PXI 和LabVIEW 的电能质量扰动检测平台进一步验证本文提出算法在强噪声环境下检测的准确性和有效性.