基于快速终端滑模状态观测器的车轮滑移率跟踪控制

张家旭，施正堂，赵健

（1.吉林大学 汽车仿真与控制国家重点实验室，吉林 长春 130022；2.中国第一汽车集团有限公司智能网联研发院，吉林长春 130011；3.浙江亚太机电股份有限公司智能汽车控制系统研究院，浙江杭州 311200）

连续、快速的车轮滑移率跟踪控制是电动汽车实现自动驾驶控制技术的基础，现已得到众多学者和汽车厂商的广泛关注.由于汽车在制动过程中呈现出动态非线性、参数不确定性等特点，给连续、快速的车轮滑移率跟踪控制器的设计带来了很大的挑战.针对这一挑战，众多学者采用鲁棒控制方法设计车轮滑移率跟踪控制器.

文献[1]将车速信息作为调度参数，采用李雅普诺夫稳定性理论和频域分析法设计了增益调度的车轮滑移率跟踪控制器.文献[2]将1/4 汽车动力学模型作为控制模型，采用非线性鲁棒控制方法设计了对参数不确定性和外界干扰具有强鲁棒性的车轮滑移率跟踪控制器.文献[3]利用径向基神经网络对系统复合干扰的无限逼近能力，设计了车轮滑移率跟踪前馈控制律，并采用鲁棒预测控制方法设计了车轮滑移率跟踪反馈控制律，车轮滑移率跟踪前馈和反馈控制律的有机结合，可以有效抑制系统复合干扰对系统稳定性和控制性能的影响.文献[4]采用最优预测控制方法设计了车轮滑移率跟踪控制器，并采用李雅普诺夫稳定性理论证明了所设计的车轮滑移率跟踪闭环系统对模型不确定性具有强鲁棒性.文献[5]充分考虑电动汽车制动系统的动态响应特性和机械约束，采用模型预测控制方法设计了车轮滑移跟踪控制器.文献[6]针对装配传统液压制动系统的汽车，分别建立增压、保压和减压控制模型，并采用Filippov 意义下的李雅普诺夫稳定性理论设计了切换控制规则，实现了目标车轮滑移率的稳定跟踪控制.文献[7]设计了液压制动系统的增压、保压和减压的模糊逻辑控制规则，实现了目标车轮滑移率的稳定跟踪控制.

除了上述鲁棒控制方法，滑模控制方法因具有较强的鲁棒性、较高的计算效率等优点，广泛应用于车轮滑移率跟踪控制器的设计.文献[8-9]采用车轮滑移率跟踪偏差作为滑模面，设计了车轮滑移率跟踪滑模控制器.由于文献[8-9]在车轮滑移率跟踪滑模控制器中引入符号函数项来抑制系统复合干扰对系统稳定性和控制性能的影响，导致滑模面上的系统轨迹存在“抖振”现象.为了抑制文献[8-9]提出的车轮滑移率跟踪滑模控制器存在的“抖振”现象，文献[10-11]将车轮滑移率跟踪偏差与其积分的和作为滑模面，设计了车轮滑移率跟踪积分滑模控制器.文献[12]基于自适应反馈递归滑模控制方法设计了车轮滑移率跟踪控制律，并采用径向基神经网络干扰观测器在线估计和补偿系统的复合干扰，从而有效避免了滑模控制方法产生的“抖振”现象.文献[13]采用二阶滑模控制方法设计了无“抖振”现象的车轮滑移率跟踪控制律，但是二阶滑模控制方法需要滑模面的导数作为反馈量.文献[14]基于自适应滑模控制方法设计了车轮滑移率跟踪指数趋近控制器，并且采用函数型连接小波神经网络干扰观测器估计和补偿系统复合干扰，从而有效地避免了自适应滑模控制方法产生的“抖振”现象.文献[15]充分考虑了制动系统的时延特性，结合反馈线性化方法和自适应滑模控制方法设计了抗时延的车轮滑移率跟踪控制器.文献[16]采用自适应积分滑模控制方法设计了对扰动具有强鲁棒性的车轮滑移率跟踪控制器，并通过参数自适应律来提高系统对路面附着条件的适应能力.上述基于滑模控制方法的车轮滑移率跟踪控制器需要系统的全部状态信息作为反馈量.因此，对于难以采用传感器直接测量的状态信息，需要设计状态观测器对其进行实时观测.

滑模状态观测器因对参数不确定性具有不敏感性，广泛应用于状态信息的实时估计.文献[17]采用滑模状态观测器实时观测永磁同步电机的转速信息，并以此为基础实现了永磁同步电机的无传感器矢量控制.文献[18]采用滑模观测器实时观测船用永磁推进电机的位置信息，并通过李雅普诺夫稳定理论给出了滑模观测器参数的选择依据.文献[19]采用滑模观测器实时观测航天器的角速度信息，并以此为基础实现了航天器姿态容错控制.上述滑模观测器的误差均是渐近收敛到零或一致最终有界的，难于实现滑模观测器与控制器的模块化设计.

鉴于此，本文基于有限时间稳定和快速终端滑模控制理论设计具有有限时间收敛特性的快速终端滑模状态观测器，该观测器采用已知的车轮滑移率跟踪误差信息，实时观测未知的车轮滑移率跟踪误差一阶导数信息，为全状态反馈车轮滑移率跟踪控制律的设计奠定基础.随后，以快速终端滑模状态观测器的观测信息为基础，采用模块化思想独立设计快速终端滑模跟踪控制律，使车轮滑移率跟踪闭环系统可以快速、准确地跟踪目标滑移率.最后，结合车辆动力学仿真软件建立模型在环测试系统，仿真验证本文提出的车轮滑移率跟踪控制器的可行性和有效性.

1 数学模型建立

简洁、高效的数学模型是控制系统设计的基础，假设汽车行驶路面平坦，并且忽略汽车悬架动态、轮胎滚动阻力和空气阻力等因素，基于Burckhardt 轮胎模型建立如图1 所示的车轮滑移率动态模型作为车轮滑移率跟踪控制器设计的基础.

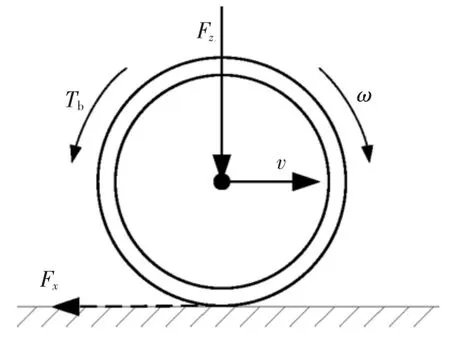
图1 车轮滑移率动态模型Fig.1 Wheel slip dynamic model

如图1 所示，基于达朗贝尔原理建立关于车轮角速度ω 和车速v 的动力学方程为[20]：

式中：J、r 和m 分别为车轮转动惯量、车轮有效滚动半径和1/4 整车质量；Tb为车轮制动力矩；Fx为轮胎纵向力，可表示为

式中：Fz为车轮垂向载荷；μ（λ）为轮胎-地面附着系数，采用Burckhardt 轮胎模型可表示为

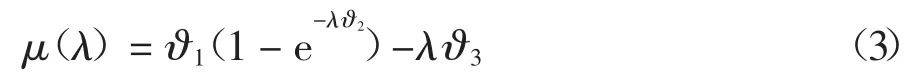
式中：ϑ1、ϑ2和ϑ3为Burckhardt 轮胎模型中表征轮胎-地面附着条件的参数；λ 为车轮滑移率，在制动工况下定义为

对式（4）求二阶导数，可得：

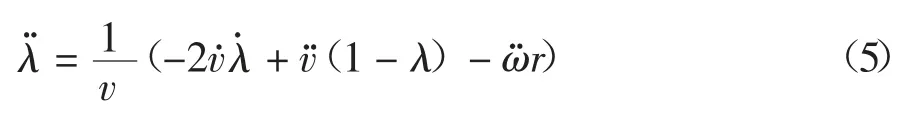
将式（1）的一阶导数代入式（5），可得：

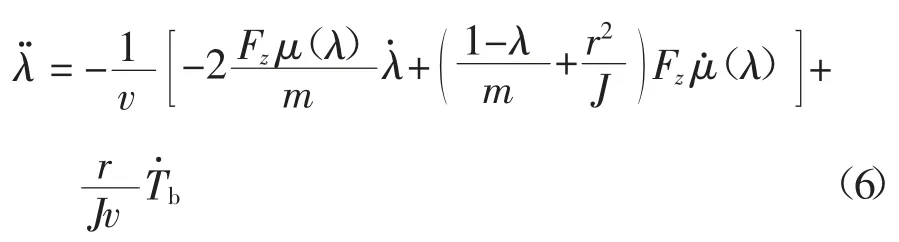
假设车轮目标滑移率为λd，定义系统状态向量和控制变量分别为则由式（6）可得车轮滑移率跟踪控制模型为：

式中：d 为模型参数摄动、未建模动态等因素引起的系统复合干扰，且满足|d|≤B1；G=r/（jv）；

2 快速终端滑模状态观测器设计

基于已知的车轮滑移率跟踪误差信息，设计快速终端滑模状态观测器，实时观测未知的车轮滑移率跟踪误差一阶导数信息，为后续全状态反馈控制律设计奠定基础.

定理1 考虑式（7）描述的系统控制模型，设计如下快速终端滑模状态观测器，即

则系统状态观测误差将在有限时间内收敛到零.

证明 由式（7）描述的系统控制模型和式（9）描述的快速终端滑模状态观测器，可得系统状态观测误差动态方程为：

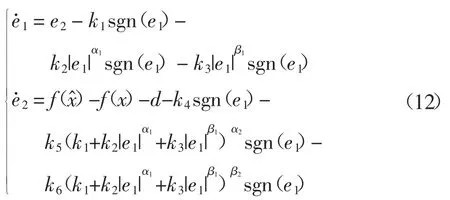
针对式（12）描述的系统状态观测误差动态方程，定义如下李雅普诺夫候选函数：

对式（13）求导，可得：

将不等式（10）代入式（14），可得：

由设计参数0＜α1＜1 和β1＞1 可知，当系统状态x1的观测误差|e1|＞1 时，式（15）右端的第二项起主导作用，驱动系统状态x1的观测误差在有限时间内收敛到|e1|=1；当系统状态x1的观测误差|e1| ＜1 时，式（16）右端的第一项起主导作用，驱动系统状态x1的观测误差在有限时间内收敛到零.同时，由比较引理可知[21]，系统状态x1的观测误差收敛到零所需的时间满足：

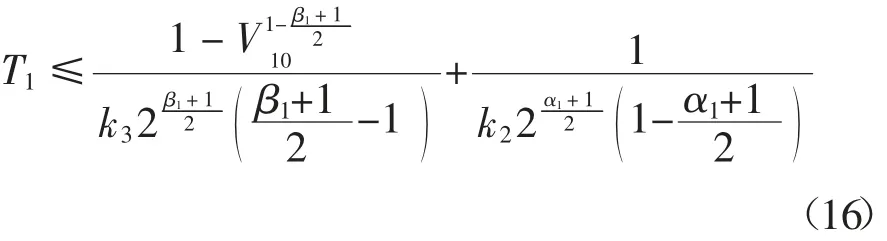
式中：V10为李雅普诺夫候选函数V1的初始值.

由等效控制原理可知，式（12）描述的系统状态观测误差动态方程可简化为：

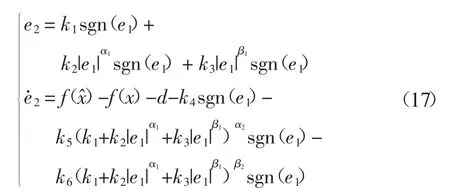
针对式（17）描述的简化系统状态观测误差动态方程，定义李雅普诺夫候选函数为：

对式（18）求导，可得：

由式（17）描述的简化系统状态观测误差动态方程可得：

将式（20）和不等式（11）代入式（19），可得：

由设计参数0＜α2＜1 和β2＞1 可知，当系统状态x2的观测误差|e2|＞1 时，式（21）右端的第二项起主导作用，驱动系统状态x2的观测误差在有限时间内收敛到|e2|=1；当系统状态x2的观测误差|e2|≤1 时，式（21）右端的第一项起主导作用，驱动系统状态x2的观测误差在有限时间内收敛到零.同时，由比较引理可知[21]，系统状态x2的观测误差收敛到零所需的时间满足：

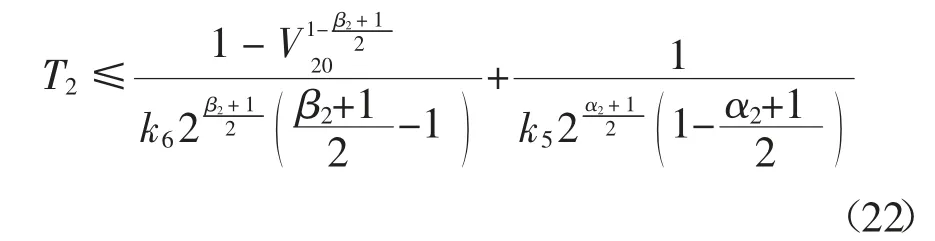
式中：V20为李雅普诺夫候选函数V2的初始值.

证毕

3 快速终端滑模跟踪控制律设计

由于第2 节设计的快速终端滑模状态观测器可使系统的状态观测误差在有限时间内收敛到零，所以可以基于模块化设计思想独立设计系统状态观测器和控制律.基于此，式（7）描述的系统控制模型可以重写为：

针对式（23）描述的系统控制模型，本节的目标是设计快速终端滑模跟踪控制律，使车轮滑移率跟踪闭环系统可以快速、准确和稳定地跟踪目标滑移率.为此，定义如下快速终端滑模面：

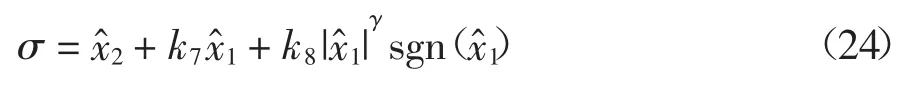
式中：k7＞0、k8＞0 和γ ＞1 为设计参数.

若系统状态轨迹位于式（24）描述的快速终端滑模面上σ=0，则有

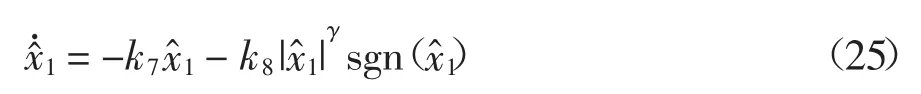
下面设计快速终端滑模跟踪控制律，使系统状态轨迹在有限时间内收敛到式（24）描述的快速终端滑模面上，从而使车轮滑移率跟踪闭环系统可以快速、准确和稳定地跟踪目标滑移率.

定理2 针对式（23）描述的系统控制模型，设计如下快速终端滑模跟踪控制律：

式中：k9＞0、k10＞0、k11＞0、0＜α3＜1 和β3＞0 为设计参数.若设计参数k9满足

则闭环系统的平衡点是渐近稳定的.

证明 定义李雅普诺夫候选函数为：

对式（28）求导，可得：

将式（23）代入式（29），可得：

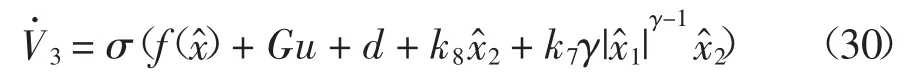
将式（26）描述的快速终端滑模跟踪控制律代入式（30），可得：

将式（27）代入式（31），可得：

由设计参数0＜α3＜1 和β3＞1 可知，当系统状态轨迹满足|σ|＞1 时，式（32）右端的第二项起主导作用，驱动系统状态轨迹在有限时间内收敛到|σ|=1；当系统状态轨迹满足|σ|≤1 时，式（32）右端的第一项起主导作用，驱动系统状态轨迹在有限时间内收敛到|σ|=0.同时，由比较引理可知[21]，系统状态轨迹收敛到|σ|=0 所需的时间满足

结合式（24）描述的快速终端滑模面上σ=0 系统状态轨迹性质可知，闭环系统的平衡点是渐近稳定的.

证毕

4 仿真分析

本节基于车辆动力学仿真软件CarSim 建立车轮滑移率跟踪控制器的模型在环测试系统，并通过干沥青路面下的阶跃递增信号仿真工况、冰雪路面下的斜坡信号仿真工况和干沥青路面下的双移线避障仿真工况验证本文提出的车轮滑移率跟踪控制器的可行性和有效性.在干沥青路面下的阶跃递增信号仿真工况和冰雪路面下的斜坡信号仿真工况中，以左前轮仿真结果为例，在鲁棒稳定性、控制精度、控制平顺性等方面对比分析本文提出的车轮滑移率跟踪控制器与基于传统滑模控制方法设计的车轮滑移率跟踪控制器；在干沥青路面下的双移线避障仿真工况中，综合分析本文提出的车轮滑移率跟踪控制器在汽车极限行驶状态下对随机目标车轮滑移率的跟踪能力.本文提出的车轮滑移率跟踪控制器参数如表1 所示.

表1 车轮滑移率跟踪控制器参数Tab.1 Parameters of wheel slip tracking controller

4.1 阶跃递增信号仿真工况

阶跃递增信号仿真工况的初始车速设置为33.34 m/s，方向盘转角设置为零，阶跃递增信号的初始幅值、递增量和目标幅值分别设置为0、0.02 和0.1.仿真结果如图2 所示.

图2 阶跃递增信号仿真结果Fig.2 Simulation results of step increment signal maneuver

由图2（a）（b）可知，本文提出的快速终端滑模状态观测器可以有效地平滑系统的状态量x1，且可以无噪声、准确地观测系统的状态量x2，为本文提出的快速终端滑模跟踪控制律实现全状态反馈奠定基础.如图2（c）～2（e）可知，传统滑模控制方法和本文提出的方法均可以稳定地跟踪目标车轮滑移率，并且对未建模动态和参数摄动具有强鲁棒性，但是本文方法对目标车轮滑移率的动态响应速度更快、跟踪精度更高.由图2（f）（g）可知，传统滑模控制方法的车轮制动力矩存在“抖振”现象，而本文方法的车轮制动力矩更加平滑.因此，本文提出方法的轮胎-地面附着系数在目标车轮滑移率稳态阶段的波动范围更小，制动过程更加平顺.综上所述，相对于传统滑模控制方法，本文提出的方法具有更快的动态响应速度、更高的跟踪精度以及更好的控制平顺性.

4.2 斜坡信号仿真工况

斜坡信号仿真工况的初始车速设置为33.34 m/s，方向盘转角设置为零，6 个斜坡信号的幅值和变化速率分别设置为 [0.05，0.07]、[0.05，-0.07]、[0.08，0.12]、[0.08，-0.12]、[0.02，0.03]和[0.02，-0.03].仿真结果如图3 所示.

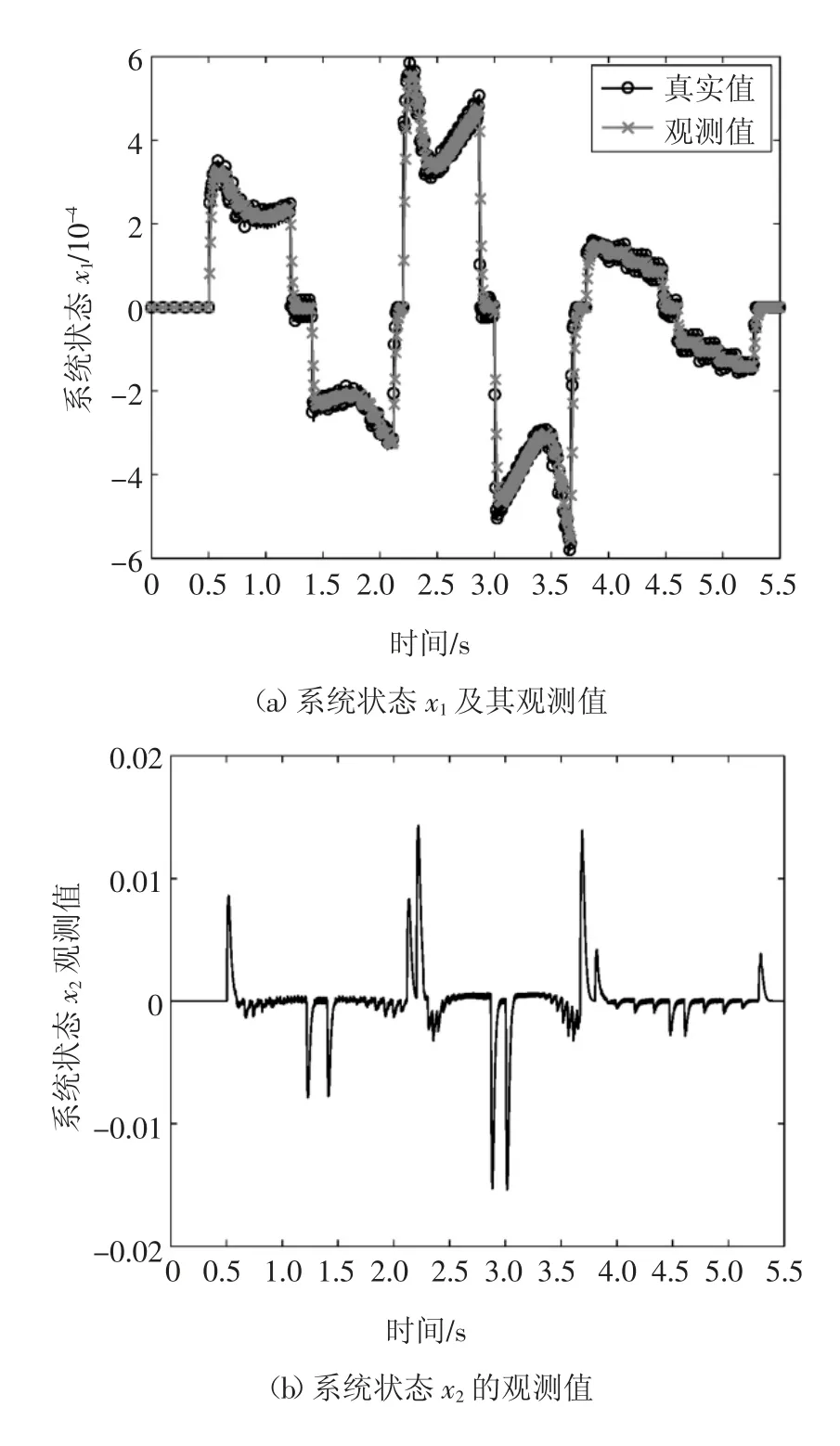
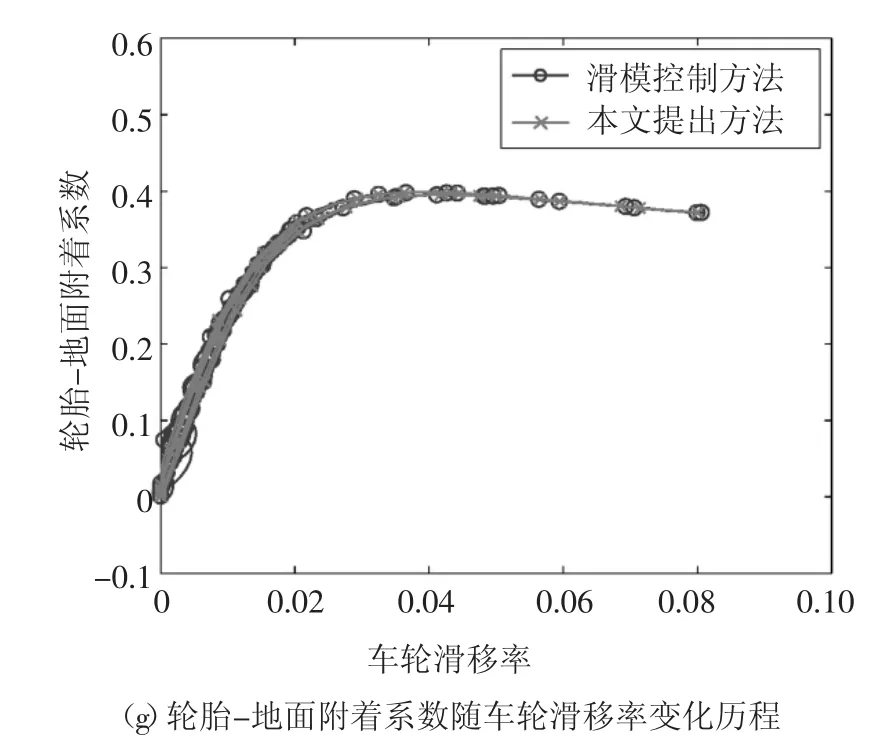
图3 斜坡信号仿真结果Fig.3 Simulation results of ramp signal maneuver

由图3（a）（b）可知，本文提出的快速终端滑模状态观测器可以有效地平滑系统的状态量x1，且可以无噪声、准确地观测系统的状态量x2，为本文提出的快速终端滑模跟踪控制律实现全状态反馈奠定基础.由图3（c）～3（e）可知，传统滑模控制方法和本文提出的方法均可以稳定地跟踪不同变化速率和幅值的目标车轮滑移率，并且对未建模动态和参数摄动具有强鲁棒性，但是本文提出的方法对目标车轮滑移率的动态响应速度更快、跟踪精度更高.由图3（f）（g）可知，传统滑模控制方法的车轮制动力矩在其峰值附近存在较大幅值的“抖振”现象，易导致制动执行机构频繁动作，而本文提出的方法可以有效地抑制“抖振”现象，使得车轮制动力矩在斜坡信号仿真工况过程中均保持平滑状态.因此，本文方法的轮胎-地面附着系数的波动范围更小，制动过程更加平顺.综上所述，相对于传统滑模控制方法，本文提出的方法具有更快的动态响应速度、更高的跟踪精度以及更好的控制平顺性.

4.3 双移线避障仿真工况

双移线避障仿真工况的初始车速设置为22.22 m/s；汽车行驶路径和前轮转向角分别如图4（a）（b）所示；车速和轮速、4 个车轮滑移率和车轮制动力矩分别如图4（c）～4（h）所示.双移线避障仿真工况的4 个车轮目标滑移率具有快变化、大幅值和强随机的特点，并且双移线避障仿真工况使汽车呈现出动态非线性、参数不确定性等特点，但是本文提出的方法依然可使汽车4 个车轮滑移率快速、稳定地跟踪随机目标信号，这说明本文提出的方法对扰动具有强鲁棒性.

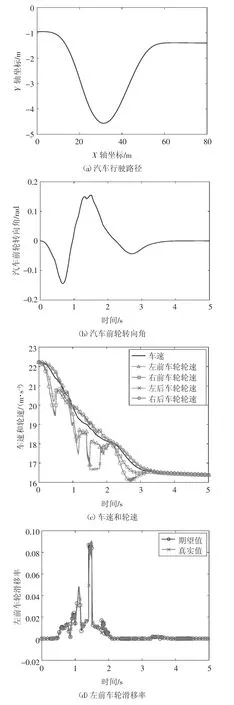
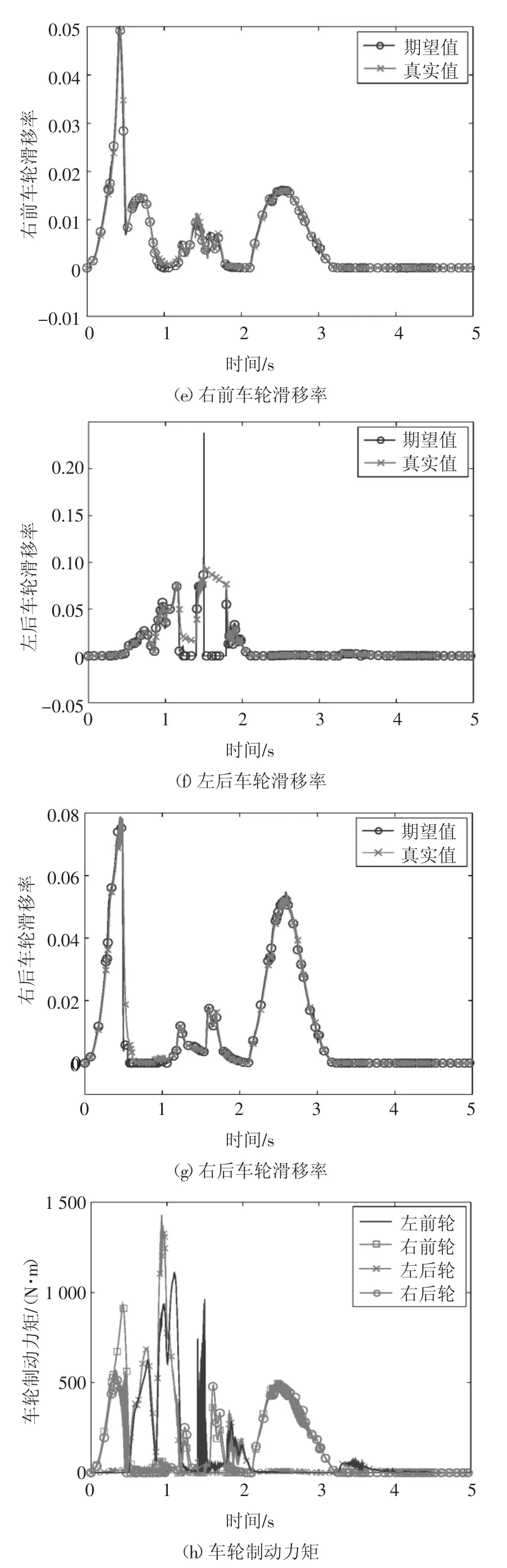
图4 双移线避障仿真结果Fig.4 Simulation results of double lane change maneuver

5 结论

本文采用有限时间稳定、快速终端滑模控制理论设计了具有有限时间收敛特性的快速终端滑模状态观测器和车轮滑移率跟踪控制器，并通过车辆动力学仿真软件对其可行性和有效性进行仿真验证.结果表明：所提出的快速终端滑模状态观测器可以准确地观测未知的系统状态信息，相较于传统滑模控制方法，所提出的车轮滑移率跟踪控制器具有更快的动态响应速度、更高的跟踪精度以及更好的控制平顺性，满足自动驾驶电动汽车对车轮滑移率跟踪控制的需求.