高铁齿轮钢18CrNiMo7-6 循环变形行为实验和本构模型

赵文杰，杨绍普，任学红，文桂林

（1.湖南大学汽车车身先进设计制造国家重点实验室，湖南长沙 410082；2.石家庄铁道大学省部共建交通工程结构力学行为与系统安全国家重点实验室，河北石家庄 050043）

齿轮传动系统是高速列车走行部关键部件，在服役过程中遭受轮轨随机激励、电机谐波振动及齿轮啮合交变循环载荷的作用，在极端工况下齿面或齿根局部会发生塑性变形的累积，进而发生破坏.因此对齿轮材料开展循环变形行为研究是很有必要的.

近年来，国内外很多学者开展了对典型金属材料的循环变形实验及其本构模型的理论研究[1-4]，并且现有的实验研究主要集中在不锈钢、铝合金和轨道钢等典型工程材料的单轴和多轴棘轮行为研究以及工程材料的循环软硬化特性.但是对于高铁齿轮钢18CrNiMo7-6 循环变形行为的实验研究，目前为止相关的研究报道还未见.在本构模型的理论研究方面，基于已有的实验结果，众多学者基于Armstrong-Frederick 非线性随动硬化模型[5]，发展和提出了更加合理的能够描述材料循环软硬化行为和棘轮行为的随动硬化模型，以此来提高模型的预测能力，比较具有代表性且应用比较广泛的模型有Chaboche模型[6]、Ohno-Wang 模型[7]、Jiang-Sehitoglu 模型[8]、Ohno-Abdel-Karim 模型[9]、Ohno-Kang 模型[10]等.但是各本构模型都有自己的优缺点，目前为止没有一种模型可以对所有材料的各种实验条件和加载工况进行准确的模拟，而且关于高铁齿轮钢18CrNiMo7-6 这种软化材料的棘轮行为的预测，相关的研究工作还比较少.

因此，在本文中首先对齿轮钢18CrNiMo7-6 展开单拉实验、对称应变循环实验和非对称应力循环实验研究，然后在循环弹塑性模型理论框架下，在Ohno-Abdel-Karim 非线性随动硬化律中引入与累积塑性应变相关的棘轮参数的演化方程，建立了修正的Ohno-Abdel-Karim 随动硬化模型，最后应用该模型模拟了齿轮钢18CrNiMo7-6 的循环变形行为，验证了改进的模型的合理性.

1 实 验

本实验所采用的齿轮钢18CrNiMo7-6 是进口材料，从德国西门子齿轮轮齿根部原位取样切割加工得到，试样取样位置及机加工流程如图1 所示.材料为18CrNiMo7-6，其主要的化学成分（质量分数，%）为 C：0.15～0.21；Si：≤0.40；Mn：0.50～0.90；P：≤0.035；S ≤0.035；Cr：1.50～1.80；Ni：1.40～1.70；Mo：0.25～0.35.将试样加工成标距段长度为30 mm，直径为8 mm 的标准螺纹试样.试样加工尺寸如图2 所示.

图1 试样取样位置及机加工流程Fig.1 Sample sampling location and machining process

图2 齿轮钢18CrNiMo7-6 的试样加工尺寸Fig.2 Specimen size of gear steel 18CrNiMo7-6

本文的实验机采用RPL100 电子式蠕变疲劳实验机，如图3 所示.具体的实验内容包括单拉实验、对称应变循环实验和非对称应力循环实验.

对齿轮钢18CrNiMo7-6 进行了单拉实验，加载的应变率分别为0.002%s-1和0.02%s-1，得到的应力应变关系曲线如图4 所示，可以看出齿轮钢18CrNiMo7-6 在不同加载率下的单拉实验曲线基本上是重合的，可以认为齿轮钢18CrNiMo7-6 黏性很小，基本上可以忽略.同时可由实验计算出齿轮钢的弹性模量E=210 GPa，屈服强度为610 MPa，强度极限为1 224 MPa.还可以看出齿轮钢在达到强度极限之前会发生明显的应变强化，之后会进入颈缩阶段.

图3 RPL100 电子式蠕变疲劳实验机Fig.3 RPL100 electronic creep fatigue tester

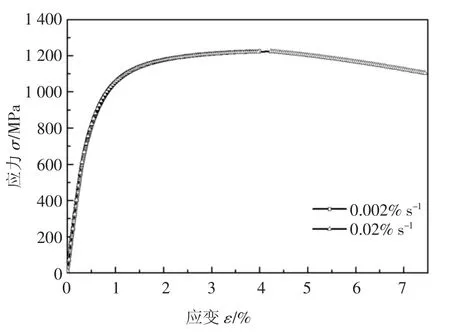
图4 齿轮钢18CrNiMo7-6 在不同应变率下的单拉实验曲线Fig.4 Monotonic tensile curves of gear steel 18CrNiMo7-6 under different strain rates

对齿轮钢18CrNiMo7-6 在应变速率0.2%s-1下开展不同应变幅值下的循环软硬化行为实验，应变幅值分别设置为±0.5%和±0.6%，得到的循环应力应变关系曲线以及响应的应力幅值与循环周次的关系如图5 所示.由图5 可知，齿轮钢18CrNiMo7-6 在应变控制循环实验中表现出循环软化特性，即响应的应力幅值随循环周次的增加逐渐减小.同时外加应变幅值越大，齿轮钢的循环软化速率越快.此外该材料的循环软化速率会随着循环周次增加而逐渐降低，但在实验研究的循环周次内并未出现软化行为饱和现象.

对齿轮钢18CrNiMo7-6 在加载应力速率为100 MPa/s 下开展了非对称应力循环下棘轮行为实验，主要研究了不同应力工况对齿轮钢的棘轮变形的影响.图6（a）给出了在应力工况（200±800）MPa 下的应力应变滞回环的演化曲线，可以看出滞回环宽度较窄，在实验周次内应力应变循环滞回环的宽度基本保持不变，会随着循环周次向前演化，但滞回环向前演化的速率比较缓慢.

图5 对称应变循环下齿轮钢18CrNiMo7-6的循环软化行为Fig.5 Cyclic softening characteristics of gear steel 18CrNiMo7-6 under symmetric strain cycling

图6（b）给出了齿轮钢18CrNiMo7-6 在平均应力为200 MPa，不同应变幅值下的棘轮应变演化曲线；图6（c）给出了齿轮钢18CrNiMo7-6 在应力幅值为750 MPa，不同平均应力下的棘轮应变演化曲线.从图中可以看出，18CrNiMo7-6 在实验研究周次内，棘轮应变演化曲线可以分为两个阶段，即棘轮应变率的衰减阶段和常棘轮应变率阶段，但是在实验周次内未出现加速棘轮应变率阶段.还可以看出齿轮钢18CrNiMo7-6 的棘轮应变会受到应力加载水平的影响，即平均应力和应力幅值越大，棘轮应变越大.

图6 齿轮钢18CrNiMo7-6 在非对称应力循环下棘轮应变的实验结果Fig.6 Experimental results of ratchetting for gear steel 18CrNiMo7-6 under asymmetrical stress cycling

2 循环弹塑性本构模型

2.1 主控方程

由于齿轮钢18CrNiMo7-6 的变形行为与加载速率无关，可认为是一种无黏性特性的材料，因此在本文中采用循环弹塑性本构模型对齿轮钢的循环变形行为进行模拟.在初始各向同性假设和小变形框架下，循环弹塑性本构模型的主控方程为[9]：

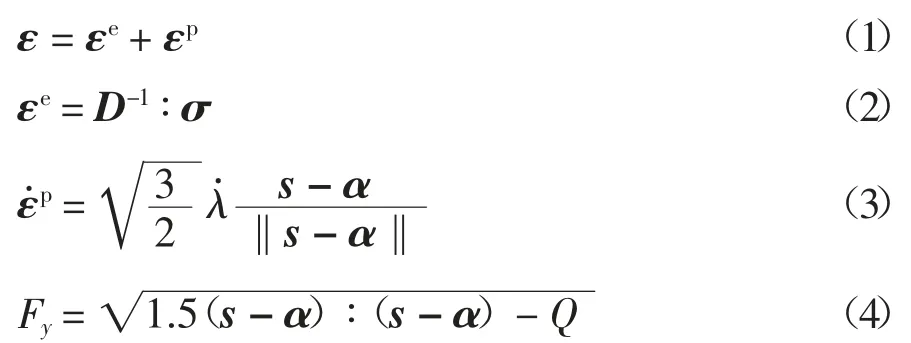
式中：ε、εe、εp和σ 分别为总应变张量、弹性应变张量、塑性应力张量和总应力张量；s 为总应力张量的偏量部分，称为偏应力张量；为塑性应变率张量，可由塑性流动方程（3）计算得到为塑性乘子，可由一致性条件计算得到；α 和Q 分别为背应力张量和各向同性变形抗力，分别表示材料屈服面的中心位置和屈服面的大小，可由随动硬化律和各向同性软化律来表征.

2.2 随动硬化律和各向同性软化律

本文基于Ohno-Abdel-Karim 模型[9]提出了一种修正的非线性随动硬化模型来描述齿轮钢18CrNi－Mo7-6 的棘轮行为，在该模型中总背应力被划分为M 个分量，即

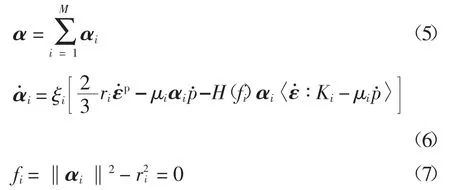
式中：αi为偏背应力分量；fi表示动态恢复的临界状态；ri为临界曲面的半径；Ki=αi/‖αi‖表示背应力分量的方向；ξi为材料常数；H（fi）为Heaviside 阶跃函数；μi为Armstrong-Frederick 模型与Ohno-Wang模型相叠加的参数，称为棘轮参数，可以控制棘轮应变的演化大小.在原始的Ohno-Abdel-Karim 非线性随动硬化模型中，μi被认为是一个常数，该模型只能模拟常棘轮应变率行为[11]，不能对齿轮钢18CrNi－Mo7-6 的棘轮应变率的演化进行合理的描述，因此为了描述齿轮钢18CrNiMo7-6 的准安静的棘轮行为，本文认为棘轮参数μi会随累积塑性应变的逐渐累积而减小，最终达到一个很小的稳定值.棘轮参数的演化规律可以表示为：

式中：μ0为棘轮参数的初始值；e2为控制棘轮演化率的参数；e1为控制棘轮参数稳定值的参数；p 为累积塑性应变.

为了合理地描述齿轮钢18CrNiMo7-6 的循环软化特性，还需要建立有效的各向同性软化模型.本文采用了由Chaboche 等[12]提出的非线性各向同性软化模型，具体的演化方程如下：

式中：Q 为各向同性变形抗力，表征屈服面的大小；Qsa为各向同性变形抗力的饱和值，因为齿轮钢为循环软化材料，所以Qsa＜Q；γ 为控制各向同性软化速率的参数为累积塑性应变率.

2.3 材料参数的确定

背应力分量的个数M 取值越大，理论上模拟的结果会越精确，但是会增大计算量，在本文中取M=8.ri和ξi的值可以由单拉塑性应变和应力曲线的实验结果确定，因为齿轮钢18CrNiMo7-6 为循环软化材料，在计算时有必要除去循环软化对材料单拉曲线的影响，同时在曲线变化比较大的过渡段需要多选一些点，然后由下式计算得出.

各向同性软化的饱和值可通过式（12）确定.

式中：Δσ 为应变循环中第一循环周次与最后循环周次在最大应变处响应的应力幅值的差值.对公式（9）两边积分可得[13]：

绘制出应变循环中最大应变处Q 和p 的关系曲线，拟合可以得到γ.

与棘轮参数有关的参数μ0、e1和e2只会影响应力循环下棘轮应变的演化规律，基本不会影响应变循环实验曲线的模拟，可由任一种实验工况下的棘轮应变曲线确定.最后由实验确定的齿轮钢18CrNi－Mo7-6 的材料参数如表1 所示.

表1 齿轮钢18CrNiMo7-6 的材料参数Tab.1 Material parameters of gear steel 18CrNiMo7-6

3 模拟结果

采用弹塑性循环本构模型和表1 中所示参数，首先对齿轮钢18CrNiMo7-6 在应变率为0.002%s-1下的单拉曲线进行了模拟，结果如图7 所示.由图7可以看出，经过修正的模型可以很好地模拟材料的单拉曲线.图8（a）给出修正的模型在应变幅值为±0.6%时循环应力应变曲线的模拟结果，图8（b）给出了应变循环幅值分别为0.5%和0.6%时齿轮钢18CrNiMo7-6 响应的应力幅值的模拟结果.由图8可以看出，修正的模型不仅可以很好地模拟齿轮钢的应变控制循环下的应力应变曲线，还可以对齿轮钢的循环软化特征进行很好的预测，即能对齿轮钢的循环软化速率随着循环周次增加而逐渐下降的现象进行合理模拟.同时该模型也能对应变幅值越大，齿轮钢的循环软化越大的现象进行合理的模拟.

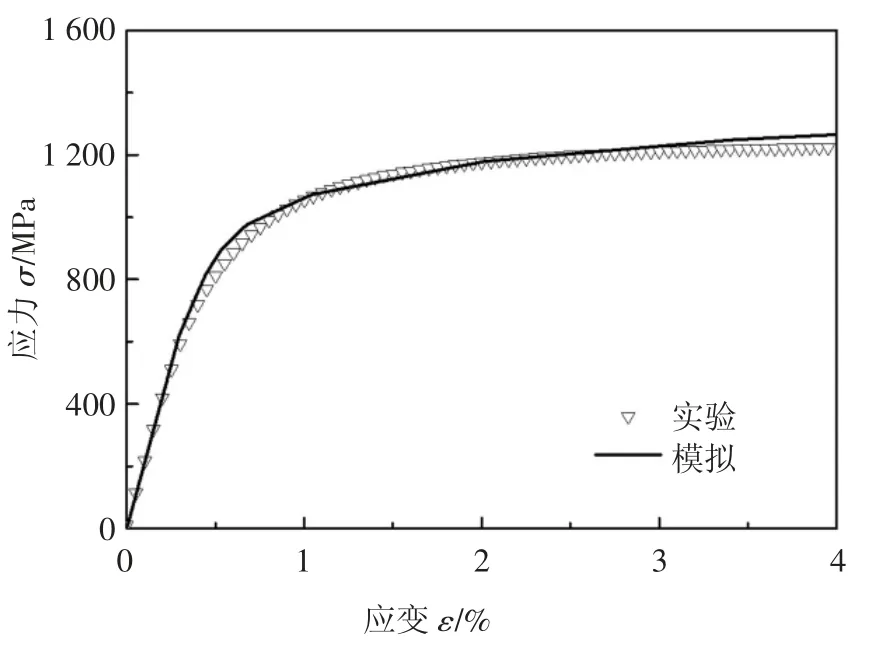
图7 齿轮钢18CrNiMo7-6 的单拉曲线模拟Fig.7 Simulated result of the monotonic tensile curve for gear steel 18CrNiMo7-6

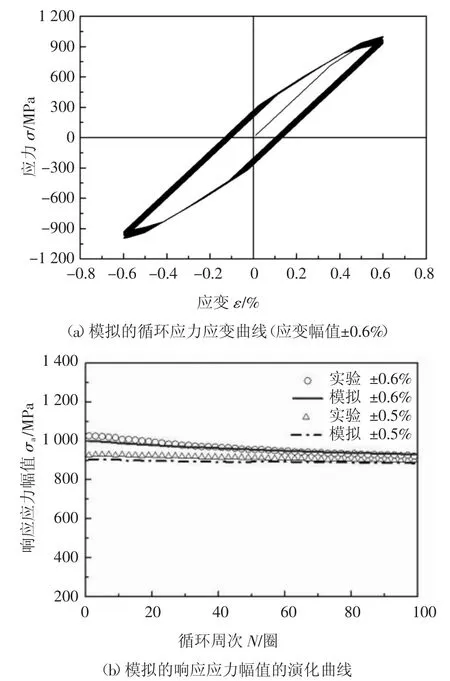
图8 对称应变循环下齿轮钢18CrNiMo7-6 的循环软化行为的模拟结果Fig.8 Simulated results of cyclic softening characteristics of gear steel 18CrNiMo7-6 under symmetric strain cycling

由于棘轮参数μ 的演化对单拉曲线和应变控制的循环实验的预测基本没有影响，只会对棘轮应变的演化规律有影响.因此，图9 给出了改进的模型与Ohno-Abdel-Karim 模型预测的齿轮钢18CrNiMo7-6棘轮应变演化曲线的对比结果.其中，图9（a）给出了平均应力200 MPa，应力幅值为800 MPa 时应力应变滞回环的模拟曲线，可以看出滞回环曲线随着循环周次向前演化，但是模拟的滞回环曲线的宽度相比实验略显宽.图9（b）和9（c）给出了改进的模型对齿轮钢在不同工况下棘轮行为的预测结果.图9（d）和9（e）给出了Ohno-Abdel-Karim 模型预测的棘轮行为的演化曲线，通过对比可以发现，原Ohno-Abdel-Karim 模型预测的棘轮应变为常棘轮应变率行为，而改进的模型不仅可以对棘轮应变逐渐增大的现象进行合理的模拟，还可以对棘轮应变率由大逐渐变小，最后保持为一个接近于零的常数的演化规律进行合理的预测.

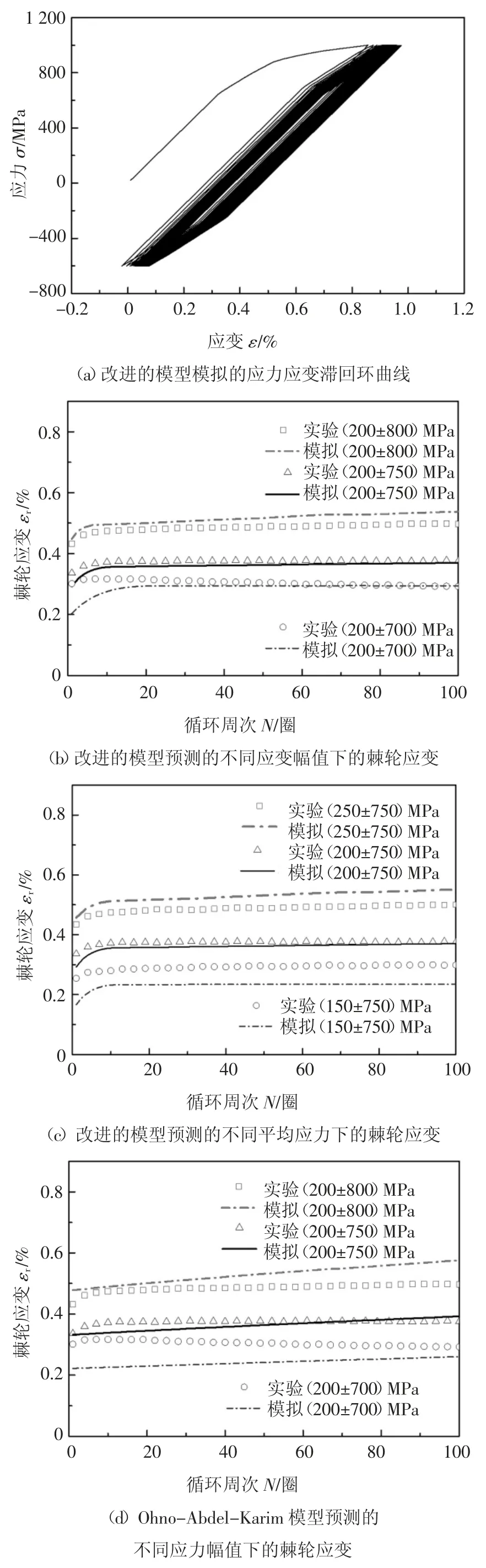
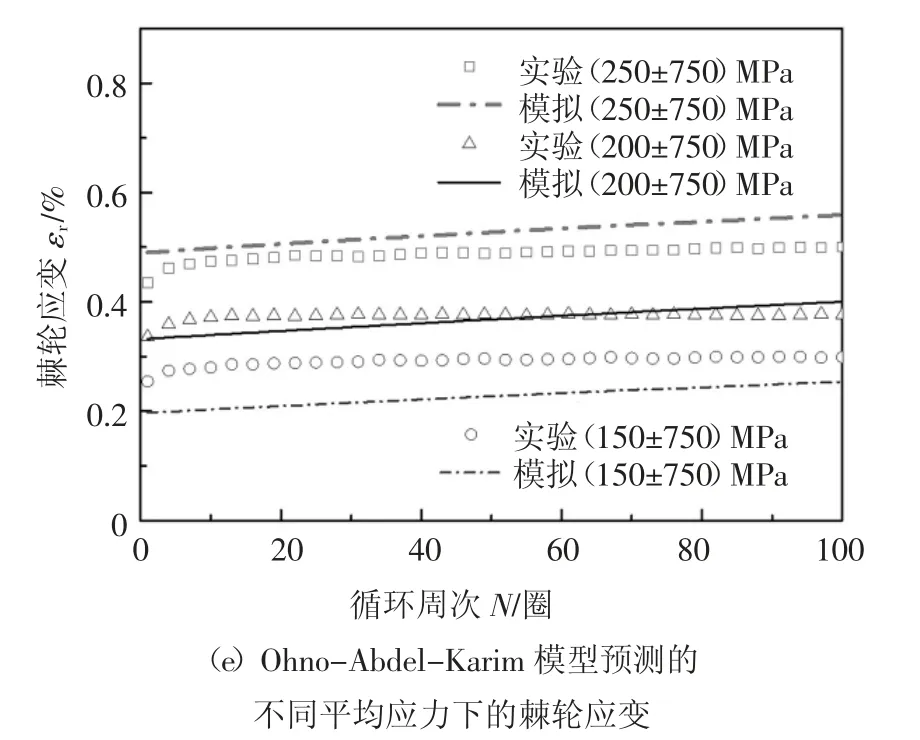
图9 改进的模型与Ohno-Abdel-Karim 模型预测的齿轮钢18CrNiMo7-6 棘轮应变的演化曲线的对比结果Fig.9 Comparison of ratchetting evolution curves of gear steel 18CrNiMo7-6 predicted by the proposed model and the Ohno-Abdel-Karim model

4 结论

高铁齿轮钢18CrNiMo7-6 变形行为与加载速率无关，因此是一种无黏性特性的材料，该材料在对称应变循环实验中表现出循环软化的特性，并且加载的应变幅值越大，材料的软化效应越明显.在非对称应力循环实验中会出现棘轮行为，在实验研究周次内表现出棘轮应变率衰减段和常棘轮应变率段两阶段，但在实验周次内未出现加速棘轮应变率段.通过在Ohno-Abdel-Karim 随动硬化模型中引入棘轮参数演化方程，不仅能够对高铁齿轮钢18CrNiMo7-6单拉曲线和应变循环下材料的软化特性进行合理的预测，而且能够有效地预测棘轮应变和棘轮应变率的演化规律.