基于增强拓扑神经演化强化学习的水面无人艇局部路径规划
2020-06-30王宝仁韩婷婷
王宝仁, 韩婷婷, 王 凯
(山东科技大学机械电子工程学院,青岛 266510)
水面无人艇(unmanned surface vessel, USV)是一种能在水面上独立航行的小型化、无人智能平台,其在军事科技和智能交通领域都发挥着重要的作用[1-2]。USV的局部路径规划问题是当前研究的热点,中外学者针对船舶自主避碰与局部路径规划问题提出了很多观点和解决方案。目前,前人多采用模糊逻辑算法或人工势场算法进行局部路径规划。王敏捷等[3]将模糊算法与近域图(ND)法相结合,提高了USV角度和速度控制的平滑性,进而提高了USV在复杂环境下的适应性;徐小强等[4]改进了经典人工势场法,优化了距离及时间,并利用YimaEnc电子海图仿真平台进行了仿真验证;Wu等[5]利用人工势场-蚁群优化(APF-ACO)算法及基于激光雷达的多层避障框架,改善了传统方法在USV导航时对障碍物检测的精度。 模糊逻辑算法可以便捷地通过模糊规则对USV进行操控且鲁棒性较高,但模糊逻辑算法存在模糊规则和隶属度函数均由经验给出、控制精较低的问题[6],因此往往不能满足控制精度要求。对于人工势场算法,虽其结构简单、路径平滑,但其存在局部极小点问题,导致路径规划失败[7]。
增强拓扑神经演化(neuroevolution of augmenting topologies, NEAT)是一种人工神经网络进化算法,具体来说是结合神经网络算法和遗传算法的一种强化学习方法[8]。基于此,对USV路径规划问题进行了数学建模,并提出了基于NEAT算法的USV局部路径规划方法,仿真对比本文方法与传统的模糊逻辑算法、人工势场算法,在路径点数目和鲁棒性方面。
1 USV局部路径规划数学模型
USV的局部路径规划如图1所示,USV需要从起始点(x0,y0)到达指定目标点(xq,yq),并根据附近的未知障碍物信息实时地对USV进行操控。将USV质点化,(xi,yi)表示第i个路径点的坐标值。

图1 USV的局部路径规划Fig.1 Schematic diagram of partial path planning of the USV
USV从此时的路径点(xi,yi)到下一个路径点(xi+1,yi+1)的递推关系为
(1)

图2 USV环境探测示意图Fig.2 Schematic diagram of the USV environment detection
式(1)中:
ψi=ψi-1+Δψi
(2)
式(2)中:ψ为USV在第i个路径点的航向角;vi为USV在第i个路径点的速度;Δψi为航向角变化量;T为每个路径点间隔的时间周期。航向角变化量Δψi和速度vi共同作为系统的输出,由此可计算得出下一个路径点。
USV环境探测示意图如图2所示,USV五个方向上的声呐传感器获得的距离信息D={dl2,dl1,dc,dr1,dr2}。设定探测的极限距离为dmax。若某方向上的声呐传感器未探测到障碍物,则该方向上距离信息值为dmax。
对于路径的优化问题,目的在于减少USV成功到达目标点时路径点的总数p,故设定目标函数为
minf=p
(3)
约束条件为
0≤vi≤vmax,i=0,1,…,p
(4)
|Δψi|≤Δψlim,i=0,1,…,p-1
(5)
式中:vmax为速度上限;Δψlim为航向角变化量极限值。
2 基于NEAT强化学习的USV局部路径规划算法设计
2.1 NEAT强化学习算法概述及实现
NEAT是一种利用遗传算法(GA)的思想进化人工神经网络的算法[9-10]。传统的神经网络演化算法在网络演化开始前,必须确定网络的结构,通过训练优化网络结构的权重。NEAT对比传统神经网络演化算法不仅对网络结构的权重进行优化,同时也对网络拓扑结构进行优化,这样就保证了演化得到的神经网络结构最简。NEAT算法借助于GA,所以算法结构也与GA类似。首先需要对神经网络结构进行基因的编码操作,之后再经过基因的变异与交叉,得到新一代个体,最后利用适应度函数计算适应度并淘汰部分种群。
为了便于神经网络间基因的杂交,基因编码采用网络连接的线性化表示,每个基因编码都有与之一一对应的网络结构。基因编码包含节点信息和连接信息,节点信息主要包括节点编号及类型,连接信息主要包括连接编号、连接的起始节点、连接的终止节点、连接的权重、标志位,其中标志位表示此连接是否有效,EN表示有效,DIC表示无效。图3为基因编码实现的示例。

图3 基因编码的实现Fig.3 The implementation of gene coding
基因的变异包括节点的增加或移除、连接的增加或移除两种形式。对于增加节点或连接,首先对新生成的节点或连接进行编号,同时赋值连接权重为符合给定正态分布的随机数。移除操作是利用标志位来实现的,当标志位以一定概率由有效变为无效时,对应连接被移除。图4为基因突变实现的示例。
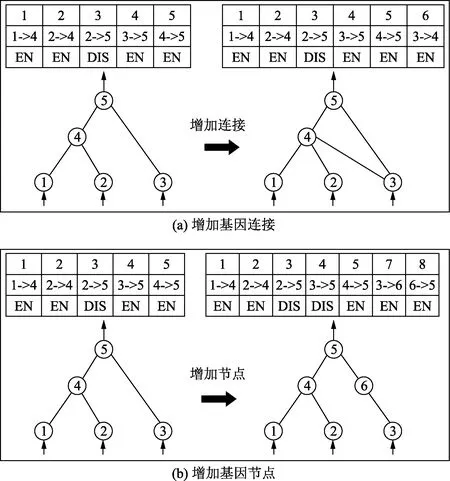
图4 基因变异的实现Fig.4 The realization of genetic variation
基因的交叉是通过父代基因编码的组合产生新的基因编码的过程。由于连接编号对应唯一的连接情况,所以后代只需继承父代的连接编号,就可以实现基因的交叉操作。图5为基因交叉实现的示例。
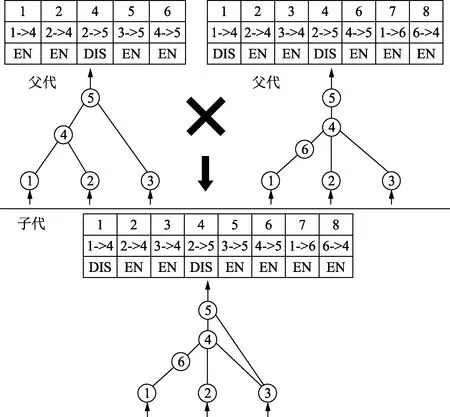
图5 基因交叉的实现Fig.5 The realization of gene crossover
新形成的个体会根据基因差别的大小区分为各个种群,竞争只存在于各个种群内部,而不是整体进行竞争。随着进化代数的增加种群数目会逐渐增多,NEAT规定一个种群进化多代后,适应度没有提高则淘汰掉这个种群,除非这个种群包含适应度最高的个体。
2.2 USV局部路径规划算法
应用NEAT强化学习算法进行USV局部路径规划,需要通过对多种情况下的地图进行训练,才能使神经网络得到进化,以演化出能够满足路径规划要求的最优神经网络。神经网络训练流程如图6所示。具体步骤如下。
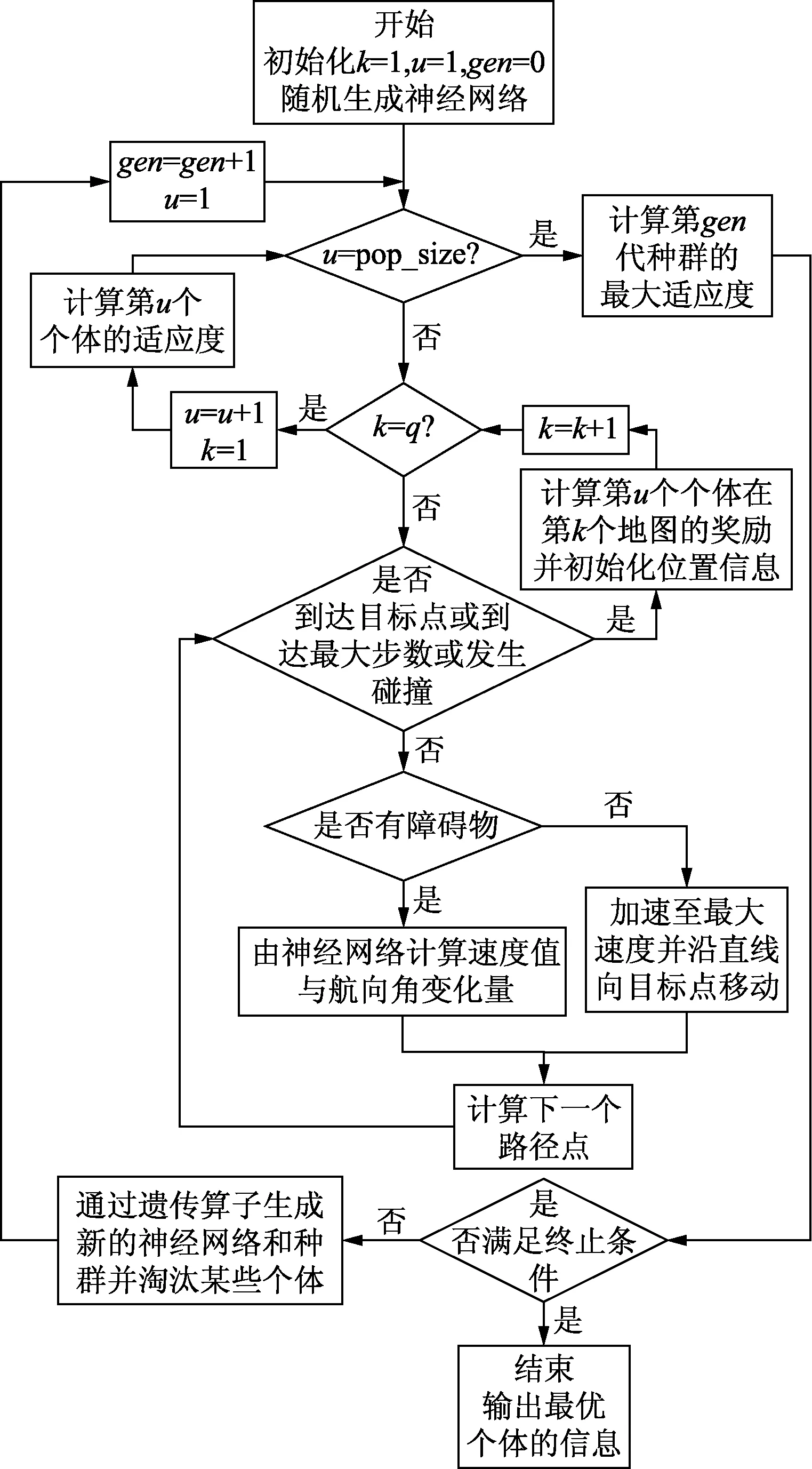
k表示地图编号;q表示训练集地图总数;u表示个体编号;pop_size表示个体总数;gen为进化代数。图6 神经网络训练流程图Fig.6 Neural network training flow chart
(1)初始化参数并随机生成神经网络结构。
(2)判断是否为最后一个个体,若否进行步骤(3),若是则计算第gen代种群的最大适应度及平均适应度,然后再判断是否满足终止条件。终止条件包括适应度达到设定阈值或进化代数达到最大进化代数,若是则结束并输出最优个体的信息,若否则通过遗传算子生成新的神经网络和种群并淘汰某些个体,然后跳转至步骤(2),进行下一代种群的训练,如此循环。
(3)判断是否为最后一幅地图,若否进行步骤(4),若是计算第u个个体的适应度,然后跳转至步骤(3),进行下一个个体的训练,如此循环。
(4)判断是否达到目标点或到达最大步数或发生碰撞,若否则进行步骤(5),若是则计算个体在单个地图的奖励值并初始化位置信息,跳转至步骤(4),进行下一幅地图的训练,如此循环。
(5)判断是否有障碍物,若否,则以最大速度沿直线向目标点移动并计算下一个路径点;若是,则由生成的神经网络计算速度量和角度变换量并计算下一个路径点。然后跳转至步骤(4),如此循环。
2.3 适应度函数的设定
适应度的计算分两步来进行,首先计算个体在单个地图的奖励值,当个体在每个地图都完成训练后,进行个体的适应度计算。个体在单个地图k的奖励值Rk在个体结束单个地图训练时进行计算。结束条件分别为USV成功到达目标点即(xp,yp)=(xq,yq)、发生碰撞即USV所有距离信息的最小值min{dl2,dl1,dc,dr1,dr2}小于安全距离dlim、达到最大步数pmax。Rk计算公式为
(6)
式(6)中:d为单个地图训练结束时的位置(xp,yp)与目标点(xq,yq)之间的距离;Cd为距离常数;Cp为步数常数。式(6)将奖励计算分为两种情况并保证到达目标点时的奖励高于未达到,当未到达目标点时奖励通过距目标点的距离计算,距离越近奖励越高;当达目标点时奖励通过步数计算,步数越少奖励越高,这与给出的目标函数[式(3)]相符。
对于个体的适应度计算,设定适应函数为个体在各个地图奖励值的平均数除以2。根据地图选择合适的Cd与Cp可以将适应度的值限定在0~1,适应度函数计算公式为
(7)
2.4 神经网络参数设定
根据NEAT算法的设定,需要给出初始的神经网络结构开始进化。初始神经网络结构如图7所示,设定初始网络结构为无隐藏层节点的全连接结构,神经网络结构的输入量包括距离信息D={dl2,dl1,dc,dr1,dr2}和USV运动方向和目标方向的夹角θ。为了到达更好的训练效果,对输入量进行归一化处理,使得输入值在[0,1]。转换公式为
(8)
(9)
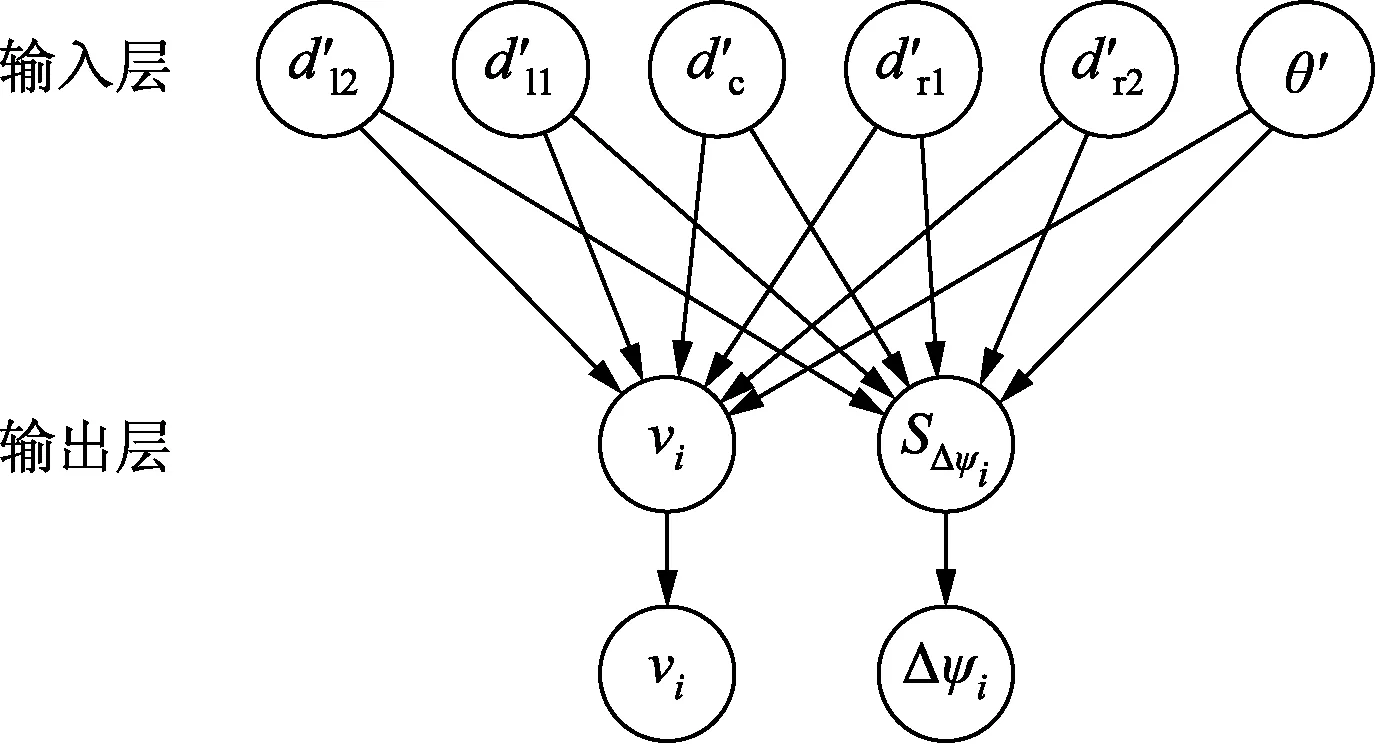
图7 初始神经网络结构Fig.7 Initial neural network structure
神经网络结构的输出层包括速度值信号Svi与航向角变换量量信号SΔψi两个节点。激励函数采用sigmoid函数,通过激励函数,输出层节点的值被限定在[0,1],再通过区间变换公式得到最终的速度vi与航向角变换量Δψi。区间变换公式为
vi=vmaxSvi
(10)
Δψi=Δψlim(2SΔψi-1)
(11)
通过变换,vi的范围为[0,vmax],Δψi的范围为[-Δψlim,Δψlim],与约束条件中的式(4)和式(5)相符。
3 仿真实验
3.1 仿真参数设定及NEAT强化学习训练
为验证所提出的局部路径规划方法的有效性和可行性,在PyCharm编译环境中,利用Python3编程语言对问题的数学模型进行模拟,借助sklearn机器学习库实现神经网络的搭建及训练过程,从而对提出的局部路径规划方法进行计算机仿真实验。与其他机器学习算法相同,神经网络的演化需要一定数量的训练集样本,研究设计了6幅地图作为训练样本,即训练集地图总数q为6。设定起始点坐标为(0,0),目标点坐标为(10,10)。设定速度上限vmax为每周期0.25个单位长度,航向角变化量极限值Δψlim为0.3 rad,探测的极限距离dmax为1.5个单位长度。取安全距离dlim为0.2个单位长度,最大步数pmax为120,距离常数Cd为15,步数常数Cp为70。NEAT神经网络演化的主要参数如表1所示。
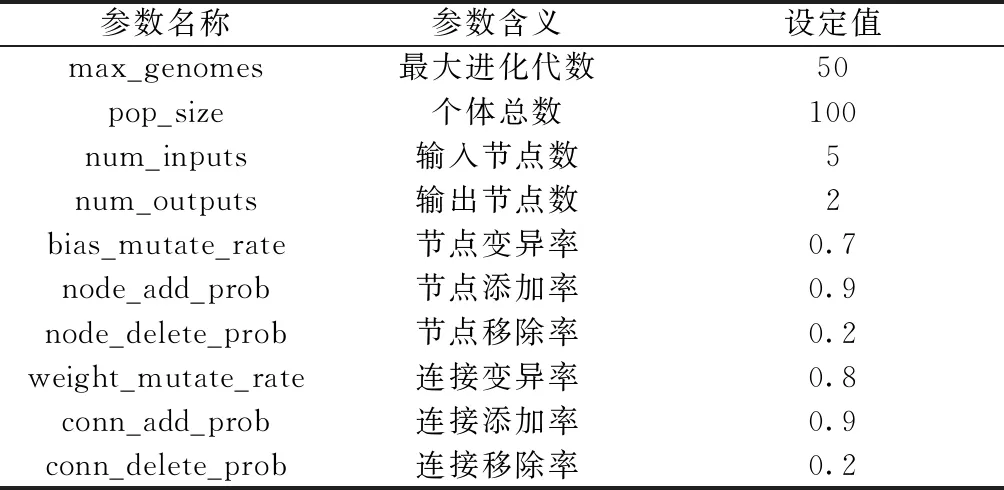
表1 NEAT主要演化参数Table 1 NEAT main evolution parameters
图8为USV训练过程中最佳适应度值与平均适应度值的变化曲线。由图8可以看出,初始种群的最佳适应度仅为0.434,经过50代的进化最佳适应度提高为0.926,平均适应度也有很大提高。图9为训练样本地图及最终演化结果。由图9可以看出,最终演化出的最优个体可以完成6幅地图的路径规划任务,且路径轨迹较为平滑。
3.2 测试及仿真结果分析
为了验证算法的鲁棒性及路径优化的有效性,利用新地图对训练得到的最优个体进行测试,并与USV路径规划中常用的模糊规则算法与人工势场算法进行对比实验,其中模糊规则算法参考文献[3]提出的模糊ND算法、人工势场算法使用文献[4]提出的引力场函数和斥力场函数。仿真结果如图10所示。图10中人工势场算法在复杂的环境中因陷入局部最小值区域而发生碰撞,导致路径规划失败。NEAT算法和模糊规则算法均完成了路径规划,路径点的个数分别为95和114。由图10可以看出,对于这幅测试地图NEAT算法路径规划的路径点数较少,路径轨迹较为平滑。为进一步验证算法的有效性,使用其他的8幅地图对上述3种算法进行对比测试,测试结果如表2所示。由表2中数据可知,人工势场算法的路径点数较少但其鲁棒性差,测试的8幅地图中只完成了6幅地图的路径规划任务。模糊规则算法的鲁棒性较高,完成了所有地图的路径规划任务,但其路径点数较多。NEAT算法完成了所有测试地图的路径规划任务且路径点数优于模糊规则算法、接近于人工势场算法。通过对比验证了NEAT算法的鲁棒性和路径优化的有效性。
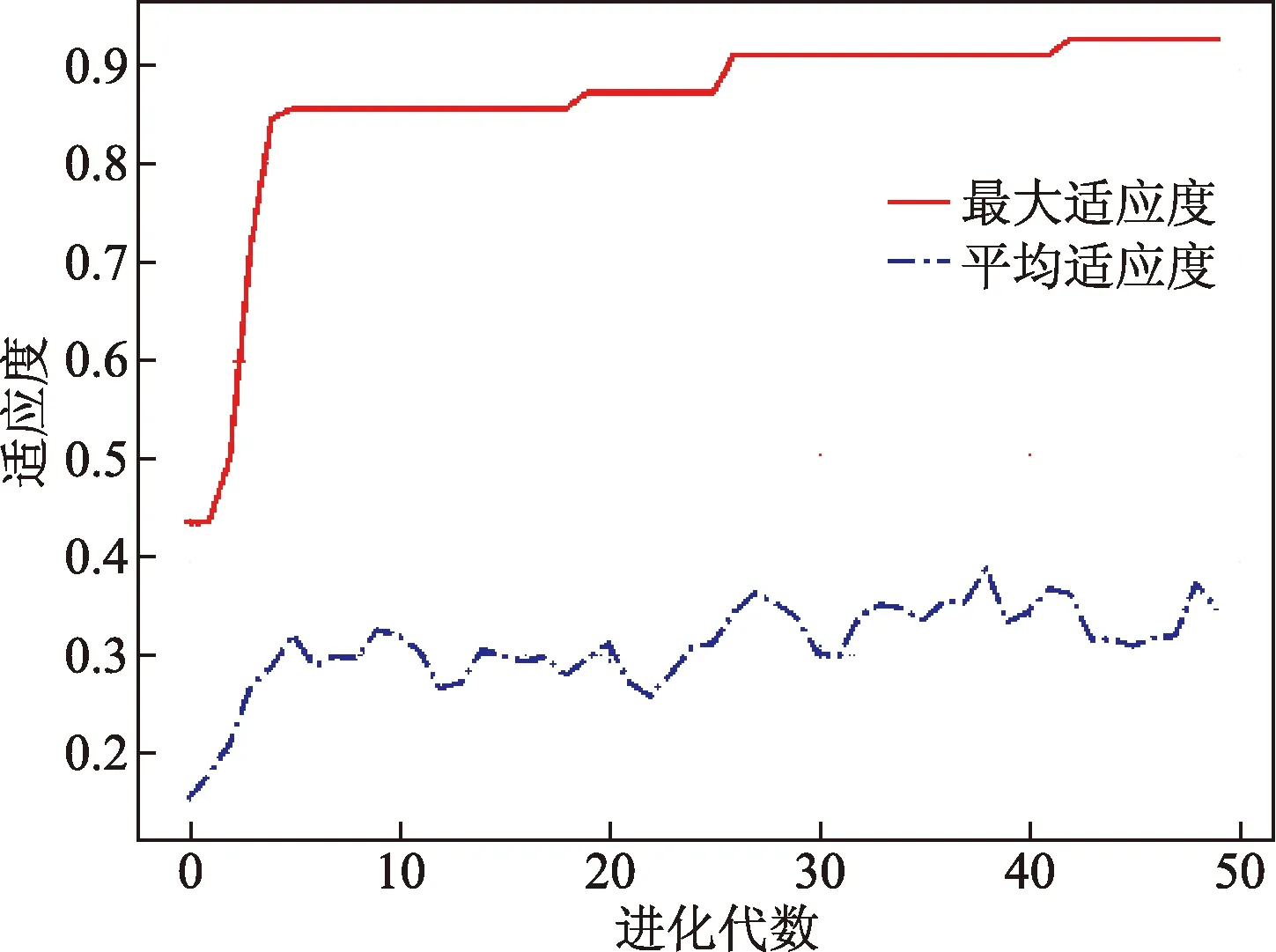
图8 适应度变化曲线Fig.8 Fitness curve

图9 训练样本地图及最终演化结果Fig.9 Training sample map and final evolution results
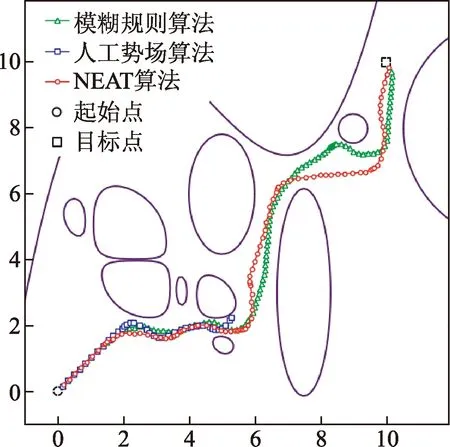
图10 对比仿真结果Fig.10 Comparison of simulation results

表2 对比测试结果Table 2 Comparison test results
4 结论
对USV路径规划问题进行了数学建模,设计了基于NEAT算法的USV局部路径规划方法,通过强化学习训练演化出能够完成USV局部路径规划任务的最优神经网络,通过仿真对比,验证了本文方法在路径点数目和鲁棒性方面,优于传统的模糊逻辑算法与人工势场算法。
由于NEAT强化学习算法具有较强的可拓展性,可将风浪或其他环境因素作为神经网络的输入修改模型后重新对神经网络进行训练,在今后的研究中将考虑这些因素使得仿真更接近于实际情况。
