高中数学教学中使学生体验“研究”魅力

承小华

(江苏省江阴市第一中学 214400)

在高中数学教学中，学生的数学应用能力与学生的研究能力有着密切联系，因此需要让学生了解到研究在高中数学教学过程中的重要性，而教师需要制定相关教师方案来让学生感受到“研究”的魅力所在.

一、结合学生特点制定教学方案——小组合作

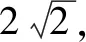
二、调整学生的研究状态与心态——情境创设

如果学生能够在课堂教学活动中获得愉悦感，则能够充分体现出教学效果，而愉悦感是保证学生能够以完美心态投入到学习过程、感受数学知识魅力的前提条件.学生在感受到学习所带来的愉悦感后，便能够对数学知识的汲取产生兴趣与热情，从而使学生的数学思维得到发散，进而能够详细分析问题与解决问题，有助于高效课堂的真正落实.就目前而言，依旧有许多高中数学教师秉承着传统教学观念，采取“一言堂、满堂灌”的教学模式，这样的教学比较枯燥和乏味，会容易让学生产生厌学的感觉，不仅不会，所以，教师在展开教学活动时，应当重视学生愉悦感的产生.比如为学生营造一个能够自由讨论的环境，或者保证学生能够在探索知识的过程中能够将自身的内在个性发扬出来，从而打造一个有着浓厚研究与学习氛围的教学环境，而教学情境的创设则是能够很好的满足学生的需求.例如，在人教版高中数学教材《同角三角函数的基本关系》中，教师便可设计相关情境来帮助学生体验研究的魅力：“对以下式子的值进行计算，其一，sin2π/6+cos2π/6 ；其二，sin2π/4+cos2π/4；其三，sin2π/2+cos2π/2，其四，sin2π/12+cos2π/12.在得出前三个式子的结果之后，同学们能够试着猜想一下第四个式子的结果吗？能用数学式子表达吗？”这种情境设计有着非常强的目的性，也就是根据“同角三角函数的平方关系”来设计相关问题，从特殊到一般形成结论.学生或许能够在老师的引导下发现“sin2α+cos2α=1”，但这种方法并不能够帮助学生拓展思维，当然也无法让学生深入研究与探索.所以，为了能够帮助学生深入研究，在研究中获得愉悦感，以此来感受数学研究的魅力，教师应该基于教材体系，以学生为主体来设计情境.首先提出问题进行引导，比如“三角函数的定义是什么？又该如何用几何法来表示它们？”然后要求学生通过三角函数的定义来求出求sin210°，同时将与之相对应的正弦值找出；之后再提出以下问题“已知第一象限角α的终边与单位圆交于点P(3/5,y)，求实数y的值；已知α是第一象限角，且cosα=3/5,求sinα和tanα的值；已知cosα=1/5，求sinα和tanα的值；已知cosα=m(|m|≤1)，求sinα和tanα的值.”通过这样的方法能够帮助学生逐步探索，自然而然地便能够体验到“研究”的魅力所在.

三、科学应用问题驱动学生研究——巧设疑问

能够引导学生研究、探索、思考与疑问的都可以被称作问题，学生在解决问题的过程中，便能够有效地体验到“研究”所带来的魅力，从而让学生喜欢上数学，同时还能够让学生在研究的过程中拓展其思维.例如，在人教版高中数学教材《直线与平面垂直的判定》中，学生最容易产生的疑惑与问题便是“直线与平面的垂直如何判定？”教师便可以将学生的问题与疑惑利用起来，让学生深入研究与探索.首先，教师提出相关问题：“如果我们通过直线与平面垂直的定义来进行评定，其方法是否能够实现？”这一问题的设计，不仅能够对学生已有的“直线与平面垂直定义”知识进行回顾与深化，同时还能够对问题解决的思路进行启发.学生通过研究后发现该定义对两者垂直的判定非常不方便.之后教师便可继续启发学生思考与研究：“在直线与直线垂直的判定上，我们都曾有过相关经验，那么这种判定对现在的问题有无启发？”这一步是通过学生已有的经验来活跃思维，使学生的学习进入到新的研究深度.最后教师再帮学生构建表象：“经过讨论和思考，直线与平面新的评定方法已经呼之欲出，但如何才能够更加形象地将这条思路显示出来呢？”为了使理解困难的那部分学生能够更清晰地掌握知识，这个时候教师便可以构建表象，比如将一个三角形沿着一个顶点折叠，同时让折叠线与对边垂直，然后再让学生观察，教师进行适当的引导，最终得出结论：“与平面内两条相交直线同时垂直的直线与该平面垂直.”从而使教学知识内容更为明晰.通过这种方法，能够使学生将旧知识应用到新情境中，有助于学生研究与探索，从而使学生在研究中体验到魅力所在.

高中数学教育是学生接受高等数学的基础所在，而让学生体验“研究”的魅力是高中数学教学的重点，也是培养学生创新性思维的前提条件，因此需要教师通过情境创设、巧设疑问以及开展小组合作的模式让学生积极主动地参与到高中数学教学之中，从而实现高效课堂.