随机泛函偏微分方程解的存在唯一性
2020-06-29余国胜
余国胜
(江汉大学 数学与计算机科学学院,湖北 武汉 430056)
0 引言
长期以来,众多学者研究了随机微分方程解的稳定性。文献[1-5]得到了相关随机偏微分方程解的稳定性,但是没有讨论解的存在唯一性。文献[6]主要研究了中立型随机泛函偏微分方程解的指数稳定性,同时也证明了解的存在唯一性。文献[7]讨论了Hilbert空间上一类随机泛函偏微分方程强解的存在唯一性。文献[8]采用变分法得到了延迟随机发展方程解的存在唯一性。文献[9]研究了无穷时滞随机泛函微分方程解的存在唯一性。文献[10]考虑了无穷维空间上随机泛函微分方程解的存在唯一性。本文在文献[6-10]的研究基础上,拟讨论更一般的可分的Hilbert空间上随机泛函偏微分方程解的存在唯一性。
1 预备知识
下面给出分析的框架。V和H是实的、可分的Hilbert空间,其范数分别为||·||和|·|,相应地V⊂H≡H*⊂V*,V*是V的对偶。映射是连续稠密的,且
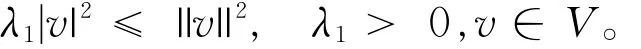
令 ||·||,|·|和 ||·||*分别表示V,H和V*中的范数,< ·,·> 表示V*和V之间的对偶乘积,(·,·)表示H中的内积。W(t)是定义在完备概率空间(Ω,ℑ,P)上取值于可分Hilbert空间K的Wiener过程,其增量协方算子为Q。{ℑt}t≥0是由{W(s),0≤s≤t}生成的σ代数,于是W(t)是关于{ℑt}t≥0的一个鞅。本文拟讨论下列随机泛函偏微分方程:
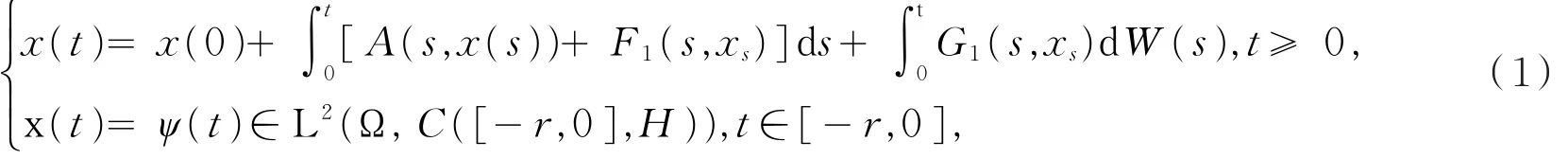
其中假设ψ是ℑ0-可测的。
A:[0,∞)× V→V*,F1:[0,∞)×C→V*和G1:[0,∞)×C→L(K,H),C=C([-r,0],H)表示从[-r,0]到H的所有连续函数全体,其中
定义1如果下列条件满足:
①x(t)∈M2(-r,T;V)⋂L2(Ω,C([-r,T],H)),T> 0,其中M2(-r,T;V)表示定义在[-r,T]× Ω上的V-值可测函数空间,且满足
∫T E-r||x(t)||2dt<∞。
②对t∈[0,T],几乎必然在V*中有下列方程成立:
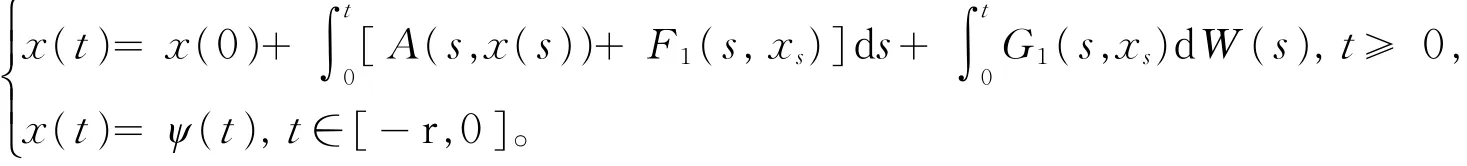
③下面的随机能量等式成立:
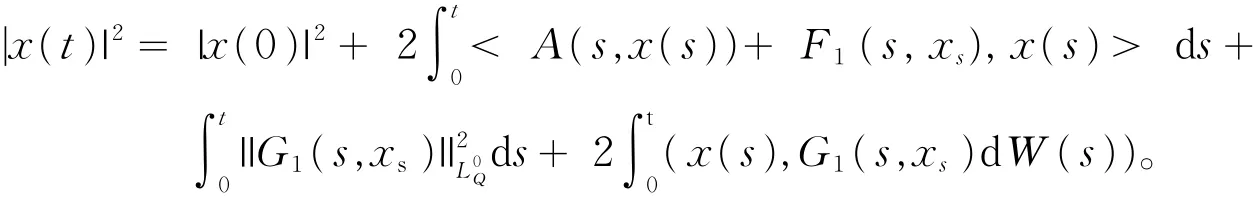
则定义在(Ω,ℑ,P)上的一个ℑt-适应随机过程x(t)为方程(1)的能量解。
2 相关引理
为得到(1)式的能量解x(t)存在且唯一,假设满足以下条件:
a1.单调、压缩条件:存在αθ> 0,λθ∈ R满足
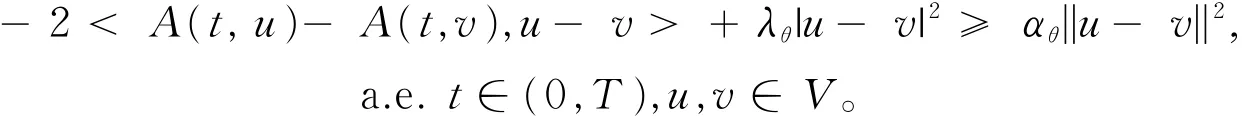
a2.可测性:对v∈V,映射t∈(0,T)→A(t,v)∈V*是Lebesgue可测的。
a3.半连续性:对u,v,w∈V,a.e.t∈ (0,T),有
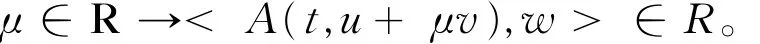
a4.有界性:对v∈V,a.e.t∈(0,T),存在c> 0使得
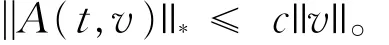
b1.Lipschitz条件:存在一个常数c1> 0,满足对于ξ,η∈C,则有
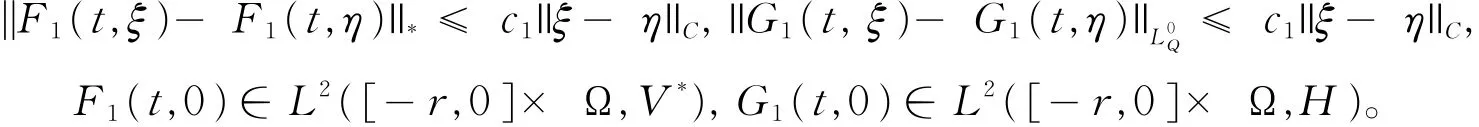
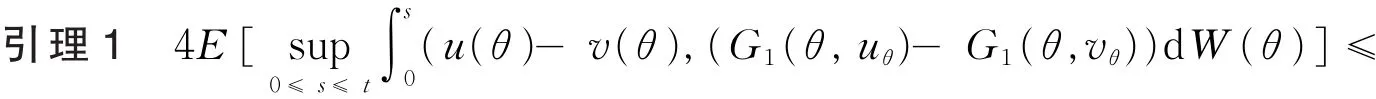

证明由Burkholder-Davis-Gundy不等式有
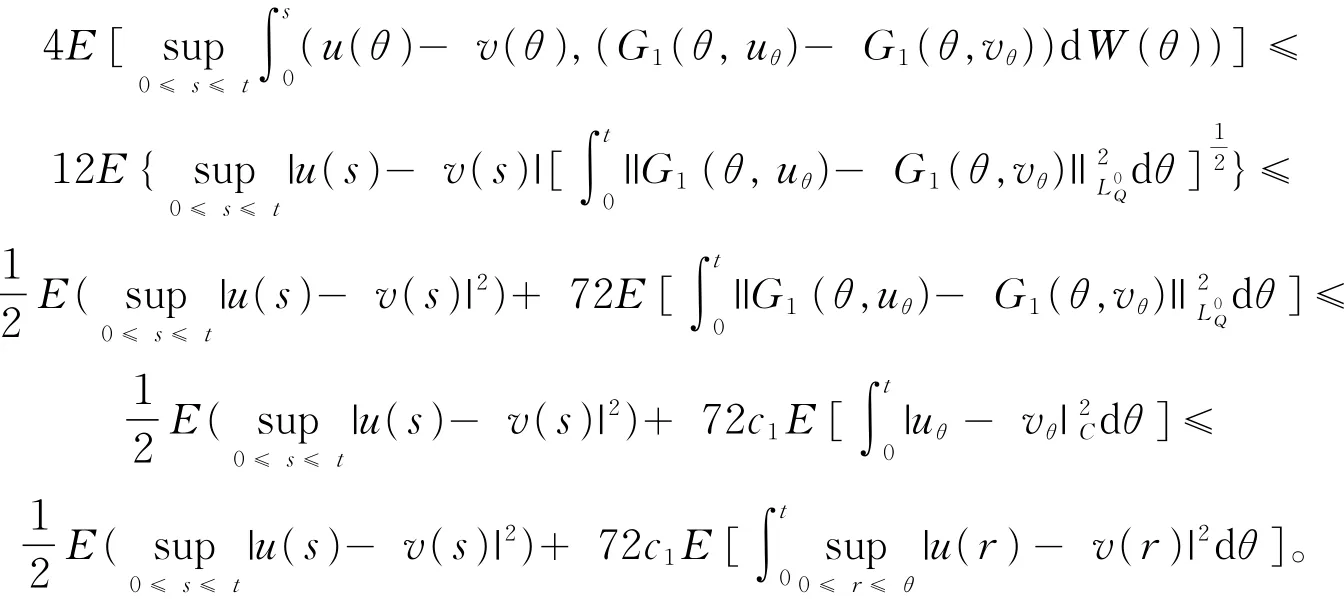
则引理1可证。
引理2令u0≡ 0,递归地定义一个过程序列{un}n≥1为
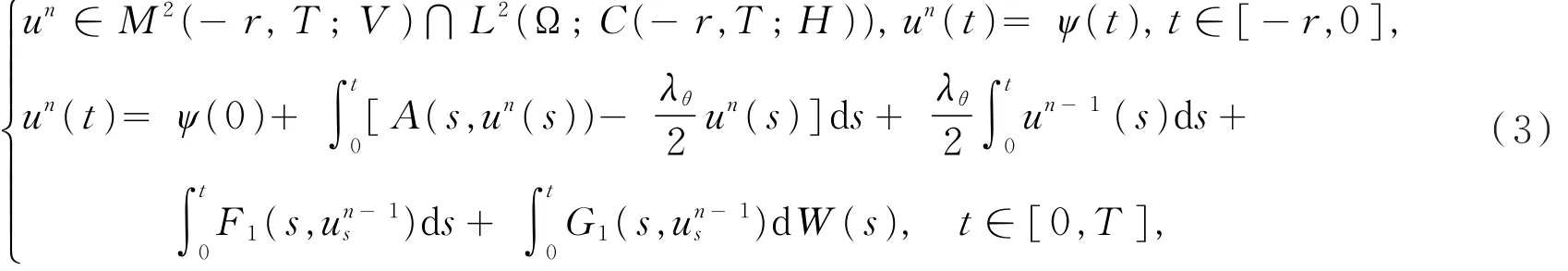
则{un(t)}n≥1是一个Cauchy序列。
证明注意到u0≡ 0∈M2(-r,T;V)⋂L2(Ω;C(-r,T;H)),由文献[11]的结果,存在唯一的un∈M2(-r,T;V)⋂L2(Ω ;C(-r,T;H))是式(3)的解。下面证明 {un}n≥1在M2(-r,T;V)⋂L2(Ω;C(-r,T;H))是一个Cauchy序列。对过程un+1(t)-un(t)运用Itô公式,且由条件a1可得
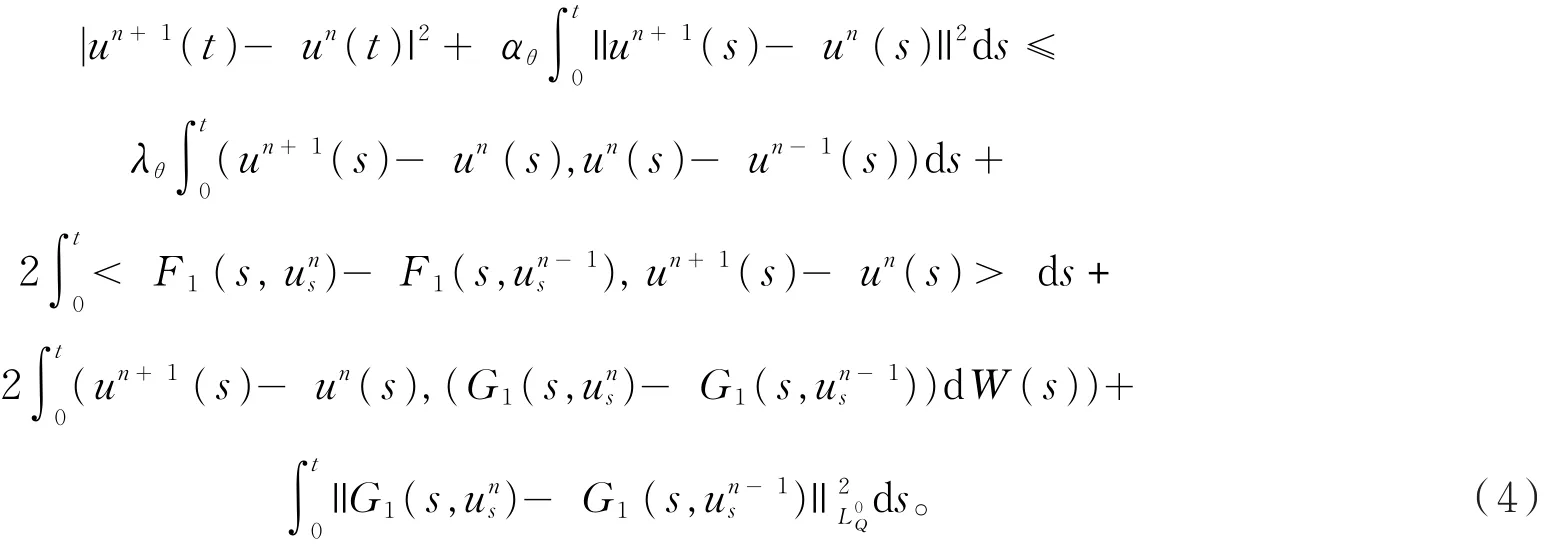
由(4)式可以得到
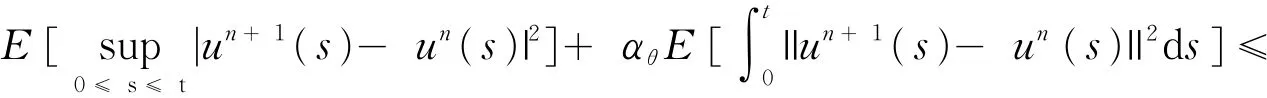
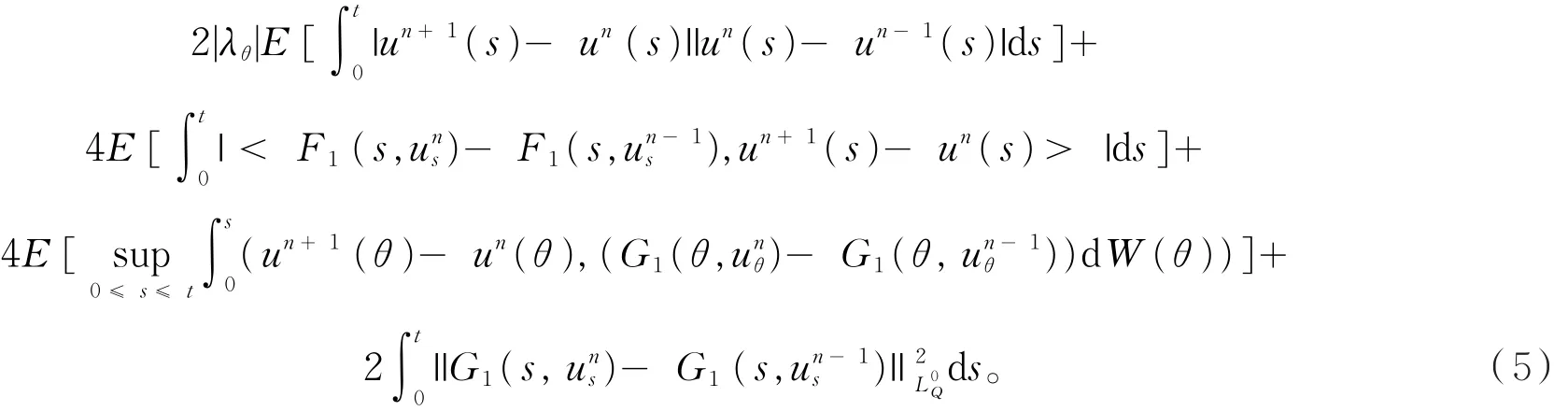
注意到
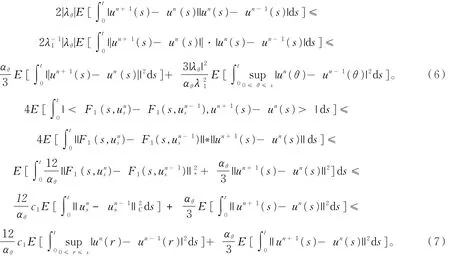
由引理1有
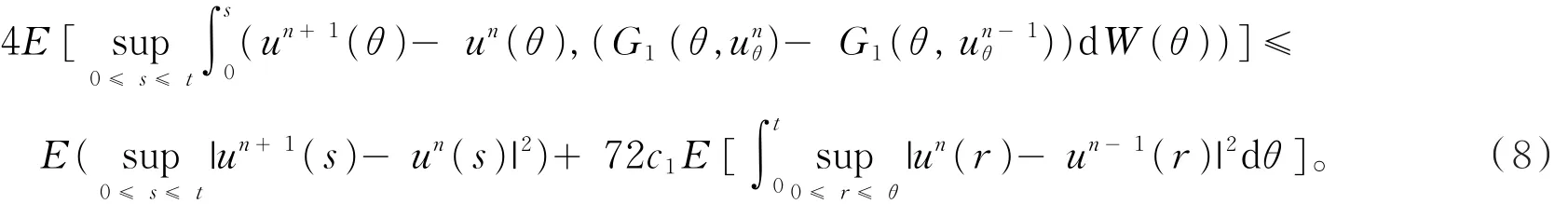
由(5)~(8)式以及条件b1,则存在一个正常数k,对n≥ 1,t∈[0,T]有
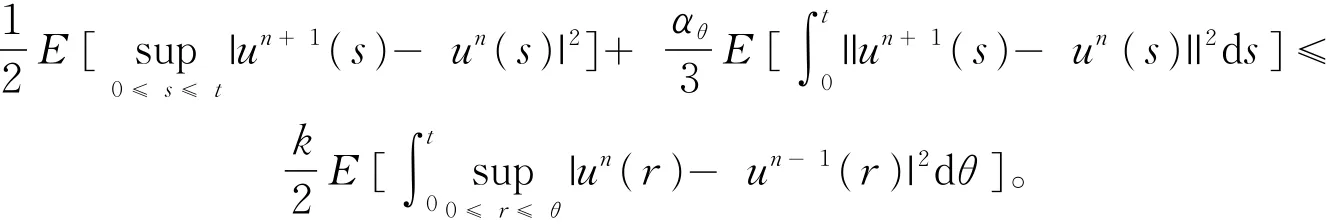
由此可以定义
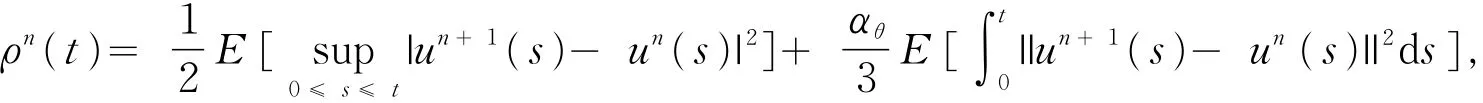
则有
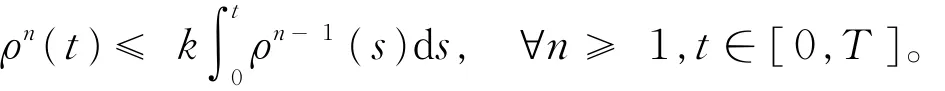
递推上面的不等式,可以得到
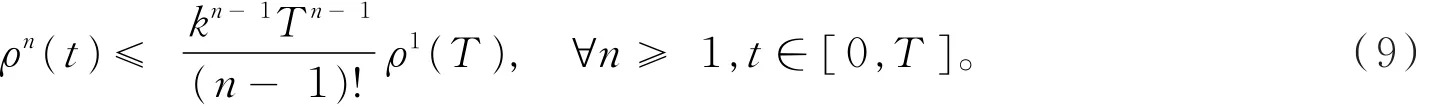
由于un+1(t)=un(t),∀t∈ [-r,0],(9)式意味着在M2(-r,T;V)⋂L2(Ω;C(-r,T;H))中{un(t)}n≥1为一Cauchy序列。
3 主要结果
定理1若假设条件a1~a4和b1均满足,则方程(1)存在唯一能量解,而且
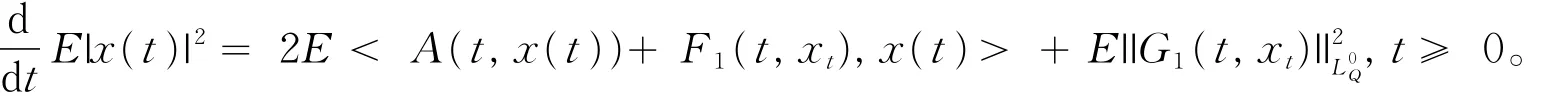
证明第一步:证解的唯一性。假设u,v∈M2(-r,T;V)⋂L2(Ω,C(-r,T;H))是方程(1)的两个解。由Itô公式和条件a1,对于∀t∈ [0,T]有
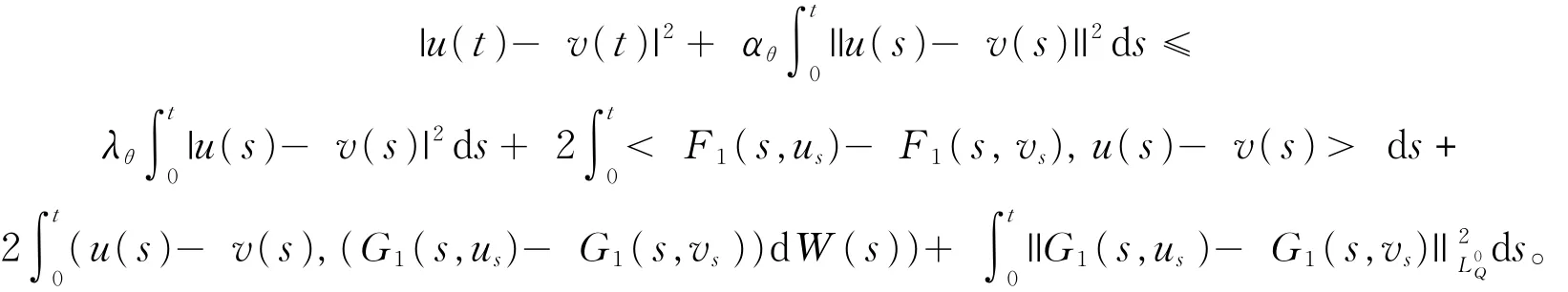
因而对于∀t∈[0,T],有
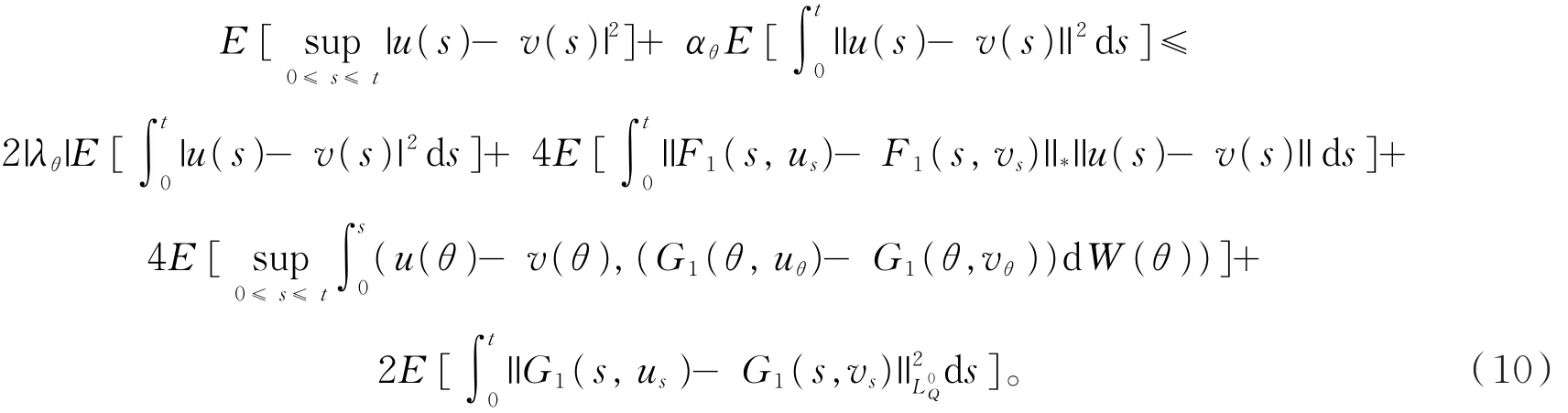
对(10)式右边估计,由条件b1,一方面
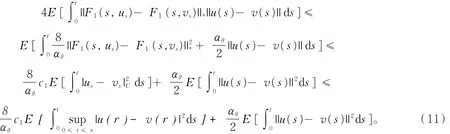
由引理1有
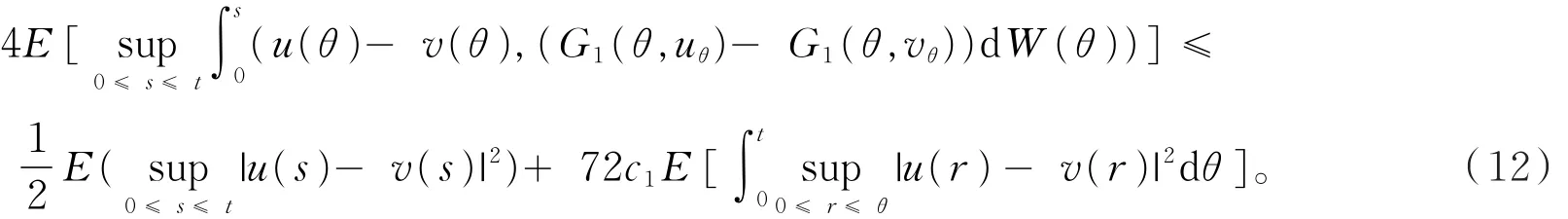
由(10)~(12)式,对于所有的t∈ [0,T],有
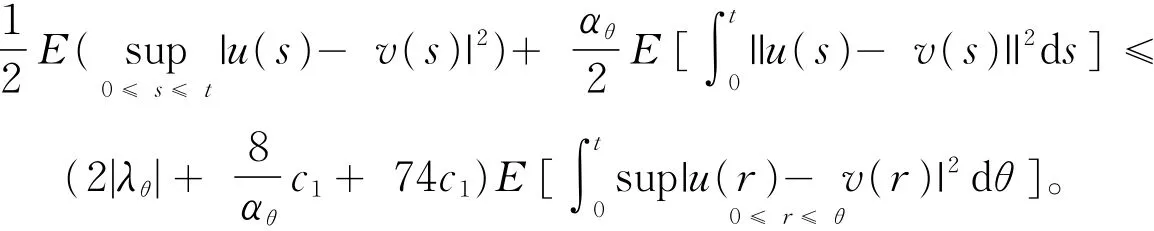
由Gronwall引理,唯一性得证。
第二步:证解的存在性。由引理2,{un(t)}n≥1为一个Cauchy序列。
方程因而存在u∈M2(-r,T;V)⋂L2(Ω;C(-r,T;H))有un(t)→u(t)。往证过程u(t)恰好是方程(1)的解。由条件b1有
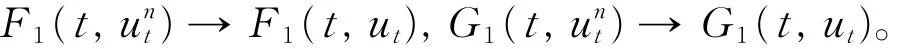
由条件a4序列{A(t,un(t))}n≥1在M2(0,T;V*)中是有界的。因而存在子序列

以及ξ∈M2(0,T;V*),使得A(t,unk(t))弱收敛于ξ,(3)式关于nk取极限,则u是下列方程的一个解。
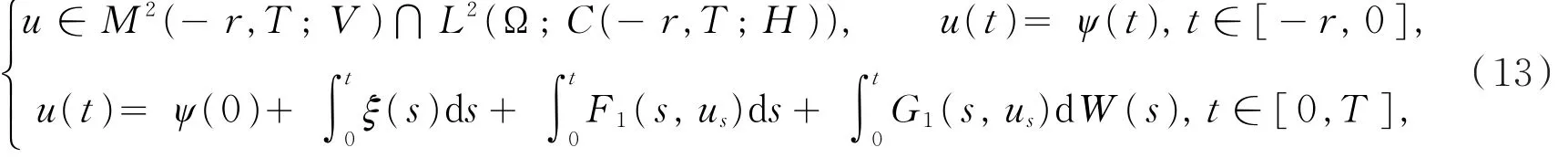
其中,ξ(t)由u(t)唯一确定,因而不妨假设在M2(0,T;V*)中整个序列{A(t,un(t))}弱收敛于ξ。为了证明u是方程(1)的解,往证ξ(t)=A(t,u(t)),t∈(0,T)。在区间[0,T]上分别对|un(t)|2和|u(t)|2运用Itô公式可以得到
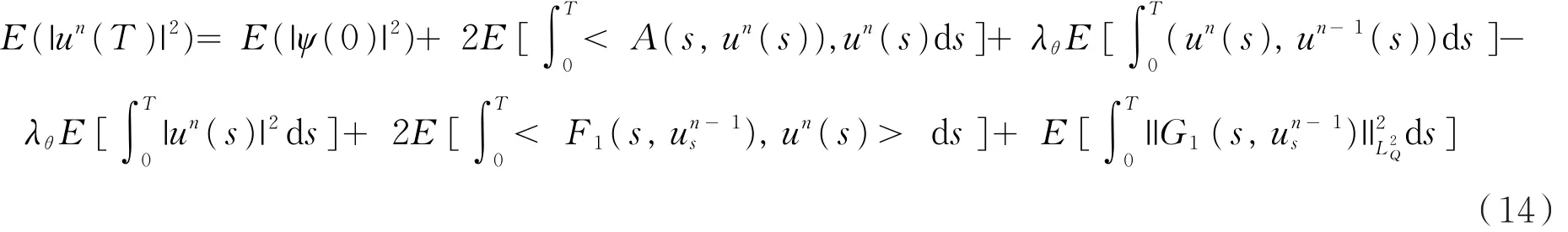
和
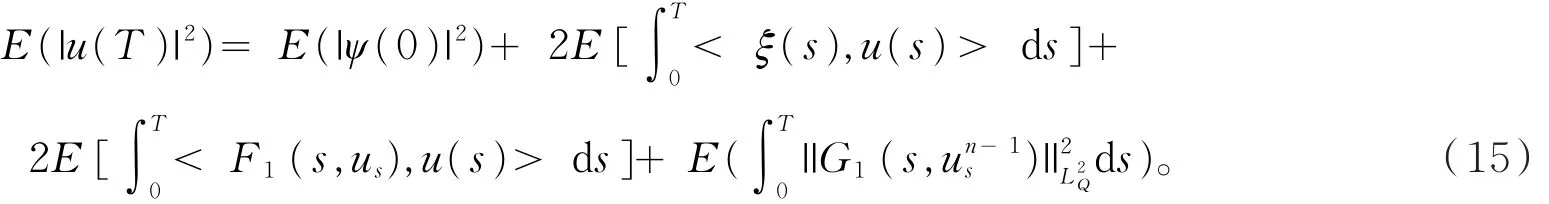
将(14)式两边取极限,并与(15)式比较有
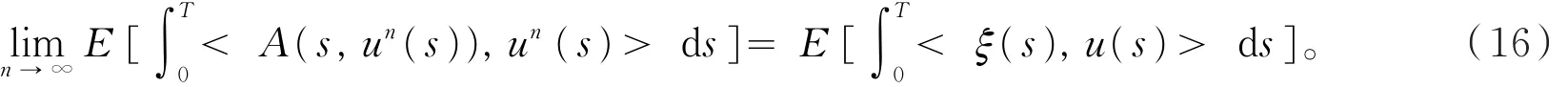
对∀x∈M2(0,T;V)和所有n≥ 1,由条件a1有
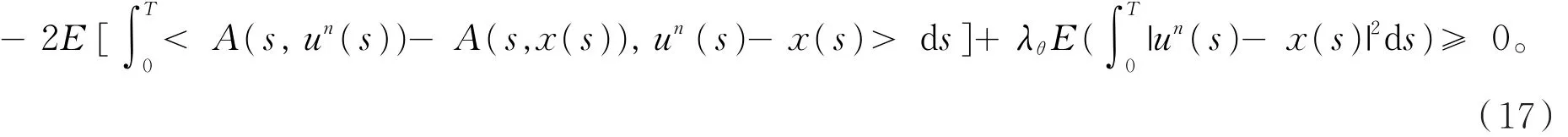
对(17)式两边取极限,∀x∈M2(0,T;V)有
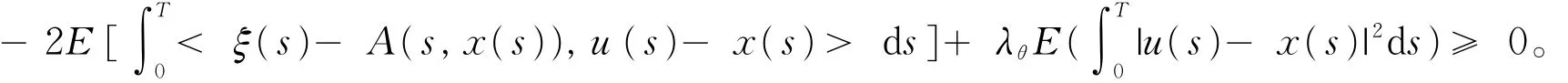
令x(s)=u(s)-δ z(s),其中z∈M2(0,T;V),δ> 0,于是
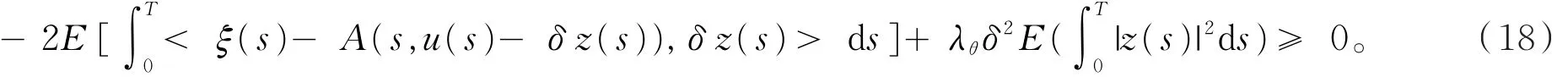
将(18)式两边同时除以δ,并令δ→ 0,由条件a3有

因而A(s,u(s))=ξ(s), ∀s∈ (0,T)。
