基于高阶滑模观测器的风机改进反演滑模控制

王 昊, 郝万君*, 曹松青, 孙志辉, 郝诗源

(1.苏州科技大学电子与信息工程学院，苏州 215009；2.丹麦科技大学电气工程系，灵比 999017)

在众多可再生能源中，风能是当今最有价值、发展最快的电力能源。为了提高风力发电机组捕获风能的能力，在额定风速以下对发电机组进行最大功率跟踪控制[1]。文献[2]中介绍了几种最大功率跟踪方法，叶尖速比法、最优转矩控制、滑模变结构控制方法等。滑模控制是一种非线性控制方法，其特点是具有良好的鲁棒性，所以越来越多的滑模控制被用在风电机组的最大功率跟踪实现上面。但是传统滑模控制中引入切换项sgns，从而产生不连续控制，所以会造成较大的抖振现象，致使发电机功率、转矩无法平滑输出，致使发电机寿命减少。文献[3]将积分滑模控制用于低风速区实现最大风能捕获，以消除稳态误差，提高鲁棒性，但未讨论滑模控制固有的抖动性以及功率输出的平滑性等问题。文献[4]利用自适应模糊终端滑模对永磁同步电机进行转速控制，有效消除了系统的抖振问题，达到了理想的控制效果。文献[5]设计基于滑模观测器的反演控制方法对压电陶瓷驱动器进行控制。利用滑模观测器解决系统的迟滞非线性问题，实现了系统的快速控制。但其反演方法中并未使用滑模控制方法。反演设计方法是一种针对控制对象的变化和环境干扰影响而提出的控制策略。文献[6]利用反演滑模的思想来解决无人艇航向的控制问题，充分体现出反演滑模控制方法对非线性的适应性及可靠性。文献[7]将反演思想与模糊控制系统结合实现了很好的控制跟踪效果。其思想是采用递归设计方法，很好地解决了对象参数不确定的鲁棒控制问题。文献[8]将滑模控制与反演控制相结合，既可以简化反演控制的设计，又可以增加系统对非匹配不确定性的鲁棒性。文献[9]针对强耦合、强非线性系统采用了高阶滑模控制与积分控制相结合的方法。该方法具有响应迅速、鲁棒性强等特点。有效克服传统滑模控制方法缺点，但是针对一些复杂非线性系统中部分状态变量未知的情况下，该方法不能完全获得系统的控制变量，进而无法完成该方法的设计。文献[10]利用滑模观测器和混合观测器相结合的方式实现无位置传感器控制，不仅节约了控制器的设计成本，而且有效解决了传统无位置传感器技术的控制缺陷，但是其系统控制器设计过程具有一定的难度和复杂性。

针对上述问题，设计了结合高阶滑模观测器的改进反演滑模控制方法。设计高阶滑模观测器(HOSMO)对不易测量的系统状态进行观测，避免了直接测量会引入高频噪声的问题。达到了更好的风电机组最大功率跟踪效果。最后在MATLAB/Simulink平台下验证了方法的有效性和可行性。

1 风力发电机组模型

1.1 空气动力模型

风轮机捕获的有效风功率Pr为

Pr=0.5πρR2V3Cp(β,λ)

(1)

式(1)中：ρ为空气密度；R为风轮转子半径；V为随机风速；Cp(β,λ)为风机功率转换效率；β为桨距角；λ叶尖速比,λ计算公式为

(2)

式(2)中：ωr为风轮转子转速。风轮转子的机械转矩为

(3)

Cp可按式(4)计算：

(4)

式(4)中:αi为近似系数;通常n取5时可以取得较高精度，α0～α5的取值如表1所示[11]。

1.2 传动系统模型

如图1所示，传动系统组成为高速轴、低速轴、

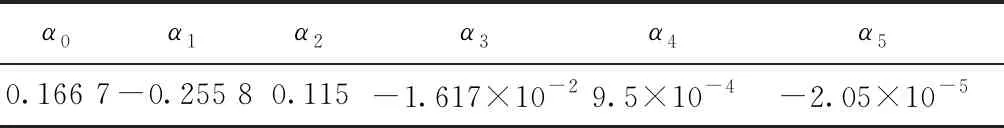
表1 近似系数取值[11]Table 1 Approximate coefficient value[11]

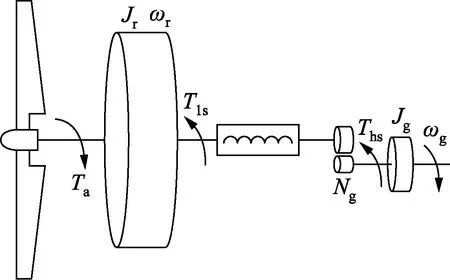
图1 传动系统模型Fig.1 Transmission system model

齿轮箱。

根据图1可知，风轮转子机械转矩Ta将以ωr的速度驱动风机。低速轴转矩Tls为转子上的制动扭矩。发电机由高速轴转矩Ths驱动，由发电机电磁转矩Tg制动。通过齿轮箱传动比Ng提高转子转速，得到发电机转速ωg。

故低速轴的动力学特性为

(5)

(6)

式(6)中:Kd、Bd分别为刚性轴的扭转系数和阻尼系数；θr、θg分别为风轮转子转动角度和发电机转动角度；θr-θg/Ng表示低、高速轴的扭转程度。

齿轮箱传动比定义为

(7)

高速轴的动力学特性为

(8)

在Ngωr=ωg始终成立的条件下，可将传动系统模型[式(5)～式(8)]简化为一个单质量块模型，故传动系统的数学模型表示为

(9)

式(9)中:Te为发电机转矩；Ng为风力机齿轮比；B为阻尼系数；J为风力机等效转动惯量；Jr为发电机转子转动惯量；Jg为涡轮转子转动惯量。阻尼系数B可以忽略不计，因为它比惯性J小得多。

1.3 风力发电机模型

采用双馈异步发电机，为简便起见，可将其描述为一个一阶线性模型[12]：

(10)

式(10)中:τg为转矩系数；Tg,ref为发电机转矩参考值。

发电机的输出功率为

Pt=ηTgωg

(11)

式(11)中：η为发电效率。

2 发控制器的设计

2.1 风电系统控制目标

根据最佳转速控制原理可知，在低风速区的控制目标是保持最佳转速比恒定在最佳叶尖速比λopt处。显然当桨距角取一些特定值时，就可以用绘出其作为λ的函数。由图2可知，当β=0o,λ=8.13时取得最大Cp，所以λ=λopt=8.13[13]。

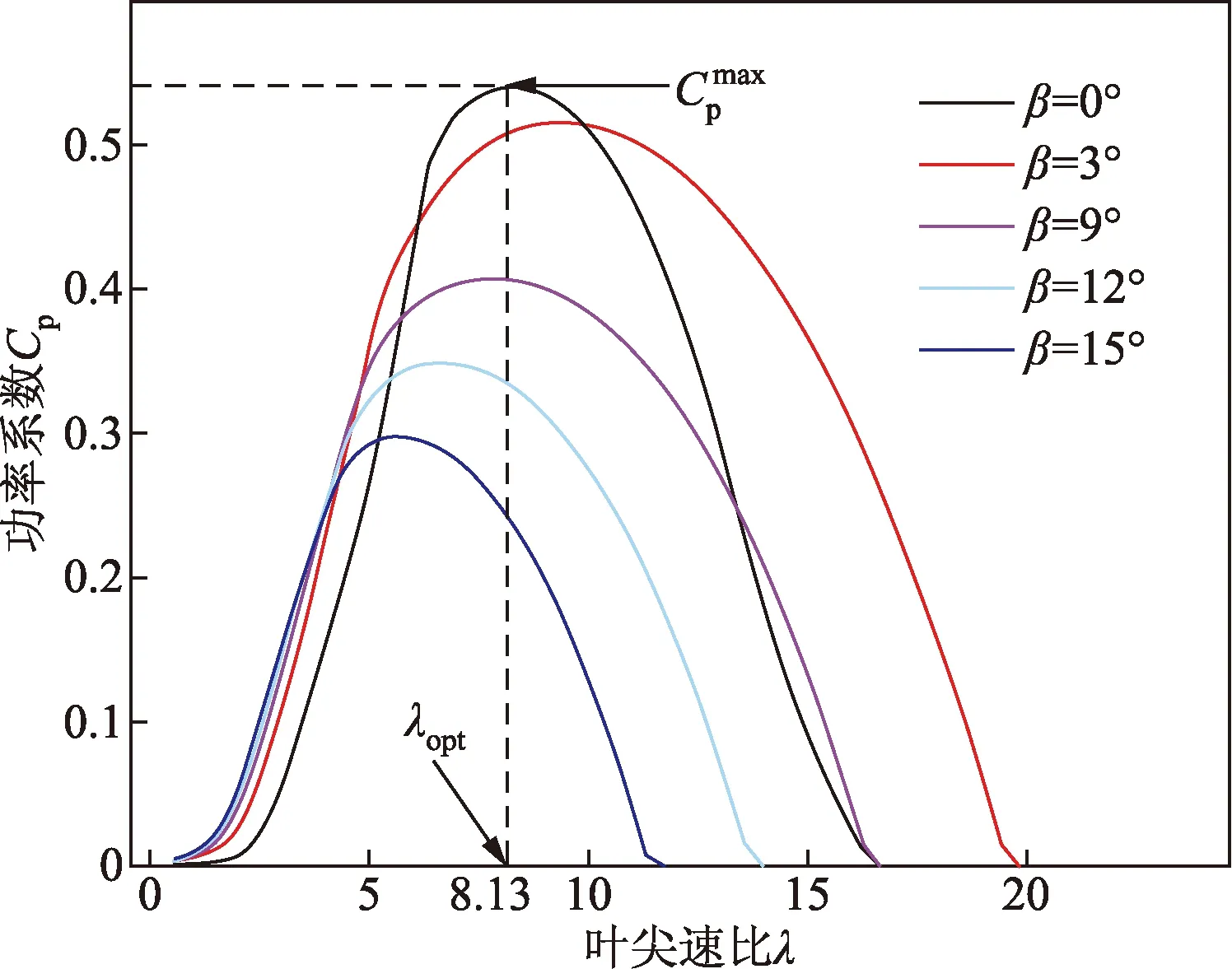
图2 风力机Cp-λ曲线Fig.2 Wind turbine Cp-λ curve

2.2 常规滑模控制器设计

传统的一阶滑模控制方法最能体现出滑模控制方法的优势。其主要表现在控制上的不连续性、强鲁棒性、对参数不敏感等优点。但同时它也能表现出传统滑模控制固有的抖振现象。为此针对风电机组进行一阶滑模控制器设计。

首先选取角速度跟踪误差为

e=ωr-ωref

(12)

式(12)中：ωref为参考角速度。

对式(12)求导,再与风力发电机的单质量模型式(9)联立得：

(13)

为了减少系统响应时间，加快系统收敛过程，选取幂次形式滑模趋近律[14]：

(14)

式(14)中：参数k和α为幂次趋近率的待设计参数，二者满足k>0,1>α>0。

将式(14)代入式(13)简化得到常规滑模控制器：

(15)

2.3 改进控制器设计

基本的反演滑模设计方法能将复杂的非线性系统分解成不超过系统阶数的子系统，然后为每个子系统分别设计Lyapunov函数和中间虚拟控制量，一直“后退”到整个系统，直到完成整个控制率的设计[14]。

由2.1节可知，风电机组低风速区的控制目标是风轮转子角速度ωr(t)实时跟踪参考角速度ωref(t)。选择系统的状态变量为x1=θr，zd=θref，x2=ωr,故定义角度误差为z1=x1-zd，即zd为参考角度，x1为风轮角度。故角速度误差为

(16)

为了克服风机系统的未知扰动和未建模动态对控制性能的影响，在反演滑模控制器设计的第一个Lyapunov函数中引入一个积分控制器，即定义Lyapunov函数为

(17)

式(17)中：λ2为反演滑模控制器的待设计参数。对式子(17)求导可得：

(18)

(19)

则:

(20)

(21)

此时引入滑模控制，定义滑动面为：s=z2。故对滑动面求导为

(22)

进而可知反演滑模控制的第二个Lyapunov函数的导函数为

(23)

(24)

式(24)中：c2、η为控制器待设计参数，二者均为大于零的正常数。

在设计滑模控制器时，可以利用饱和函数的方法进行进一步消除抖振，即用一种新的非线性切换函数替代原来的s。如式(25)所示：

(25)

式(25)中：Δ为任意的小正常数，取Δ=0.15。

2.4 改进控制器稳定性分析

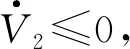
由式(23)可知：

(26)

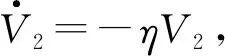
V2(t)=V2(0)e-ηt

(27)

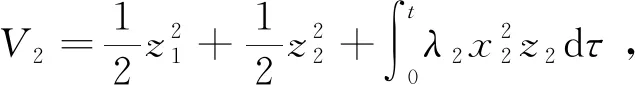
3 高价滑模观测器的设计

从2.3节可知，滑模面导函数[式(22)]和控制律[式(24)]中都含有x2的信息。然而在实际系统中，直接对状态变量x2测量会有高频噪声产生,所以引入该信号会在系统产生高频噪声。为了避免这个问题，设计高阶滑模观测器如下。

考虑：

(28)

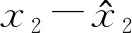
(29)

(30)

(31)

综上，具有高阶观测器的反演滑模控制器可以表示为

(32)

采用了基于HOSMO的超扭曲滑模控制，大大提高了滑动面的收敛精度。使得状态变量更接近于平衡点。故由式(16)、式(19)、式(28)、式(29)、式(32)可得功率跟踪控制系统结构如图3所示。

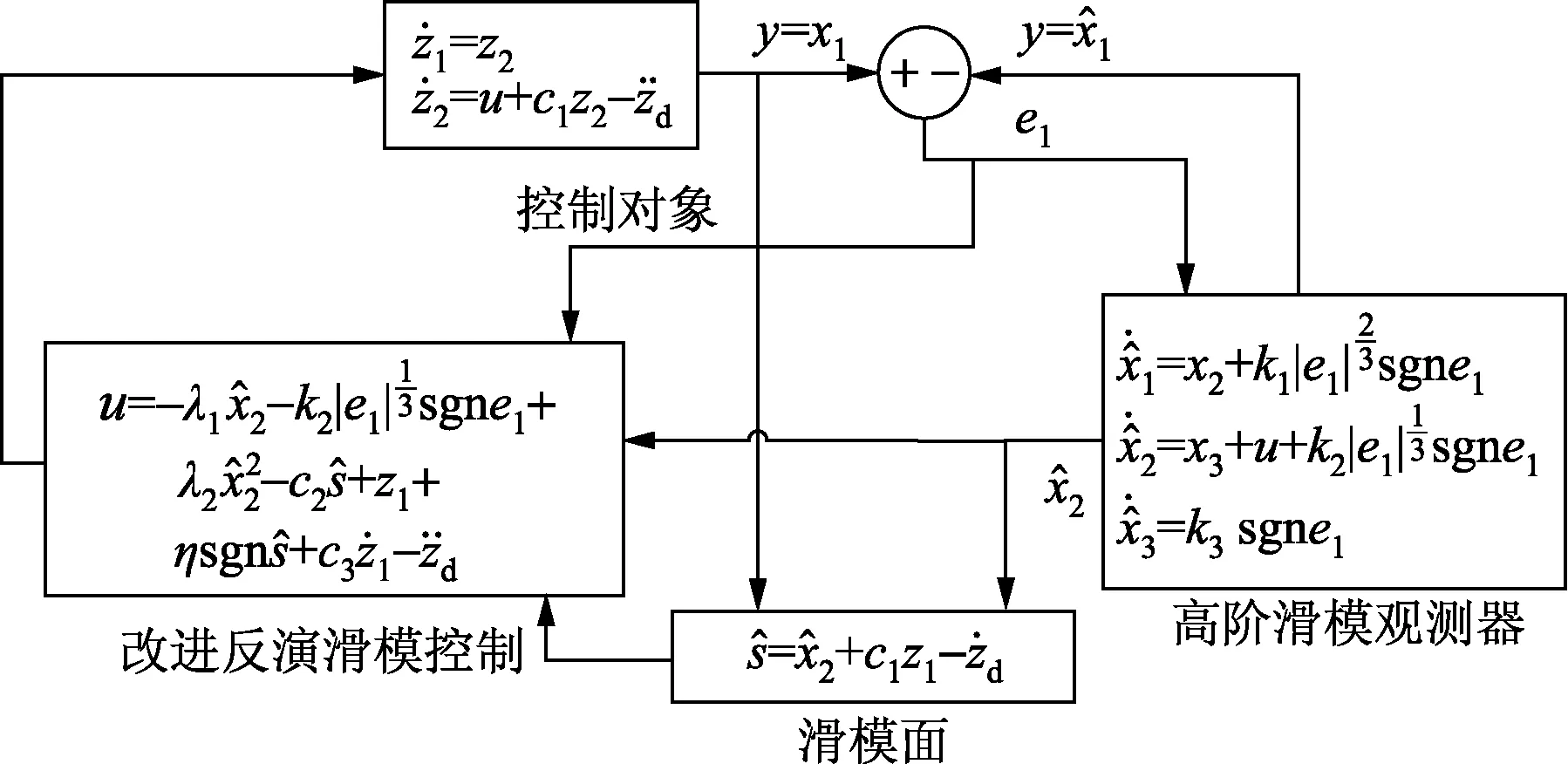
图3 风机控制系统结构图Fig.3 Structure diagram of wind turbine control system

4 仿真分析及结果

为了验证所提控制策略的最大功率跟踪性能，以实验室美国国家能源部可再生能源实验室(National Renewable Energy Laboratory,NREL)研发的 5 MW 风电机组模型为研究对象。5 MW风电机组的主要参数如表2所示。

控制器参数取值为：η=0.5，c1=141，c2=0.1，c3=3×104，λ1=120，λ2=1.71，k1=11 000,k2=-20 650,k3=12 000。

表2 风电机组的主要参数Table 2 Main parameters of wind turbines

图4 仿真实验曲线Fig.4 Curves of simulation experiment

图4为仿真实验曲线。图4(a)为400 s的湍流风速曲线，采用NREL开发的TURBSIM软件生成，平均风速为7.5 m/s。

从图4(b)可以看出：改进反演滑模比传统反演滑模和常规滑模的控制跟踪效果好，可以明显看出所提控制策略能快速地跟踪渐变风速，并且抖振较小。

从图4(c)可以计算出,所提出的控制策略得到的叶尖速比平均值为8.510，而传统反演滑模控制的叶尖速比平均值为8.953，常规滑模控制的叶尖速比平均值为10.426。所以在不同的随机风条件下，提出的控制策略比常规滑模和传统反演滑模更能使得叶尖速比接近8.13。

从图4(d)可以看出，设计的高阶滑模观测器能实时估计风轮转子转速ωr，确保了改进反演滑模控制器的计算准确，达到了想要的控制效果。

从图4(e)～图4(g)可以看出，设计的控制策略在平滑功率输出、减少转矩抖振和最大风能捕获方面都比传统反演滑模控制和常规滑模控制的控制效果要好。为了更加直观地比较三种控制策略的效果，分别计算图4中不同控制策略的输出功率平均值[AVG(Pe)]，功率系数平均值[AVG(Cp)]和发电机转矩标准差[STD(Tg)]。计算结果如表3所示。

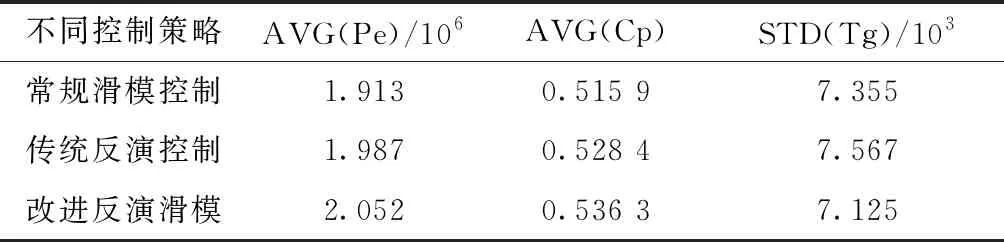
表3 三种方法的控制性能对比Table 3 comparison of control performance of the three methods

由表3可知，相比于传统的反演滑模控制方法和常规滑模控制方法，设计的控制策略能实现较大的功率输出、且抖振较小、风能捕获能力强。可计算出相对于传统反演滑模控制提高了3.27%的功率输出，创造出了更多的经济效益。

5 结论

为了提高大惯量风力发电机的能量转换效率。同时，考虑输出功率的平滑、抑制发电机转矩抖振。设计了一种适用于低风速区运行的非线性控制器。在反演滑模控制的基础上进行改进设计，并设计出高阶滑模观测器来估计风电机组中不易测量的状态，避免了直接测量引入的高频噪声，有效增强了控制跟踪效果。最后与现有的常规滑模控制和传统反演滑模控制进行了比较。研究发现在降低驱动链条瞬态负载的情况下，所提出的方法在最优功率捕获、平滑功率输出、抑制转矩抖振方面优于传统的控制方法。