基于改进应变楔模型的大直径桩基水平承载力分析方法
2020-06-29邢康宇吴文兵张凯顺
邢康宇,吴文兵,张凯顺,刘 浩
(1.中国地质大学(武汉)工程学院,湖北 武汉 430074;2.中国地质大学(武汉) 岩土钻掘与防护教育部工程研究中心,湖北 武汉 430074)
由于工程建设的需要,大直径桩基础的使用越来越广泛[1],尤其是多应用于大型桥梁和海上风电机组以承受水平荷载,这些结构物往往对大直径桩基础的侧向位移有着较高的设计精度要求,因此准确计算大直径桩基的水平承载力尤为重要。目前关于桩基水平承载力的计算方法有许多,比如m法[2]、弹塑性方法[3]、p-y曲线法[4]和应变楔模型[5]等传统方法,主要根据桩身侧向位移确定桩侧径向地基土反力,以计算桩基的水平响应。大直径桩基的承载特性往往与中、小直径桩基有着较大区别[6],已有研究表明[7-9],采用上述传统方法计算得到的大直径桩基水平承载力往往小于相应的原位试验实测值,且这一误差随着桩径的增加而变大。基于这种现象,Liang等[8]基于有限元模拟结果提出了适用于大直径单桩的p-y曲线;Kim等[9]对p-y曲线的极限地基土反力的计算进行了改进,以考虑桩径的影响。然而,Gerolymos等[10]指出,对于大直径桩等基础的水平承载特性而言,桩侧径向地基土反力并不是抵抗基础侧向位移的唯一作用来源,基础与地基土体由于接触位移产生的桩侧摩阻同样发挥了作用。因此,桩侧摩阻的影响在大直径桩基的水平响应分析中不容忽视,而仅对p-y曲线进行修正不能直接反映桩侧摩阻的影响。基于这种思想,一些学者将桩侧摩阻和桩侧径向地基土反力单独考虑,对大直径单桩的水平响应进行计算。如Ashour等[11]基于应变楔模型[5]开展了桩侧摩阻对桩基水平承载力的影响研究,但其所采用的应变楔模型忽略了桩身位移线性变化假设会造成的一些问题和矛盾[12],且其所使用的地基土体应力-应变表达式也较为复杂,仅针对试验用土而不适于推广[13];李洪江等[7]基于m法在桩基水平承载力计算中考虑了桩侧摩阻的影响,其计算较为简便,但无法考虑地基土的非线性力学特点;此外,Borden等[14]指出,大直径桩基在水平荷载作用下桩底会发生转动和位移,桩端土体会对桩底变形产生抵抗弯矩和剪力,将对大直径桩基水平承载力的计算产生一定的影响。而这些研究[7,11]并未同时考虑桩侧摩阻、桩端弯矩和桩端剪力对大直径桩基水平响应的影响。竺明星等[15]基于p-y曲线法同时考虑了上述因素的影响,获得了桩身位移与受力响应的半解析解,但计算方法较为复杂。
针对上述问题,本文在前人研究的基础上,不同于p-y曲线法,将传统的应变楔模型进行了改进,据此计算桩侧径向地基土反力,并考虑桩侧摩阻、桩端弯矩和桩端剪力3个因素对大直径桩基水平响应的影响,建立了基于改进应变楔模型的大直径桩基水平承载力的计算分析方法。通过算例分析并与现场试验的实测结果进行对比,验证了本文方法的可靠性和准确性,在此基础上进一步研究了桩侧摩阻、桩端弯矩和桩端剪力对大直径桩基水平响应的影响程度,探讨了大直径桩基水平承载能力随桩径变化的尺寸效应。
1 大直径桩基水平响应的计算
1.1 考虑桩侧摩阻的桩身侧向位移的微分控制方程
大直径桩基的受力与变形计算分析图见图1。以桩顶中点为原点建立坐标系,横坐标y代表侧向荷载作用下桩身产生的侧向位移(m),纵坐标z代表地基埋深(m)。图中,D和Lb分别表示桩基的桩径(m)和埋深段桩长(m);pt和Mt分别表示桩身泥面处承受的水平荷载(kN)和弯矩(kN·m);p表示单位桩长承受的径向地基土反力(kN/m),分布在桩身上部和下部被动侧,由桩侧被动受压土堆栈 产生,用以抵抗桩身侧向位移;τv表示桩侧单位面积承受的摩阻(kPa),即桩侧摩阻,由桩身与被动区土体之间产生的接触位移所引起,将对桩身侧向位移产生抵抗作用;Mb和Qb分别表示由桩端土体所产生的抵抗桩底变形的桩端弯矩(kN·m)和桩端剪力(kN)。
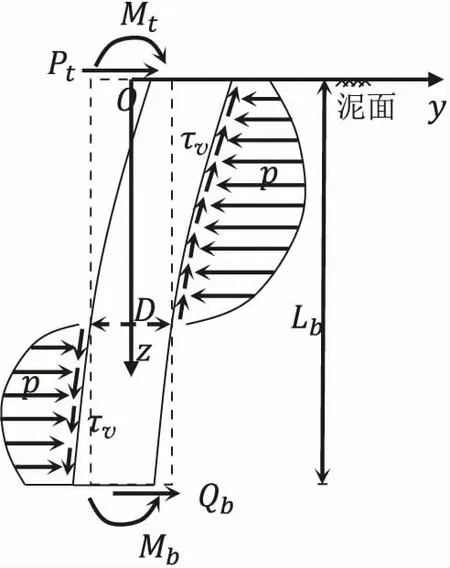
图1 大直径桩基的受力与变形计算分析图Fig.1 Diagram for calculation and analysis of force and displacement of large diameter piles
传统的桩基水平承载力计算方法往往仅考虑径向地基土反力p的作用,而忽视了桩侧摩阻τv、桩端弯矩Qb、桩端剪力Mb的作用,可能无法准确地计算大直径桩基的水平承载力。本文将分别考虑上述因素,对大直径桩基的水平承载力应进行计算。大直径桩身单元体受力图,见图2。
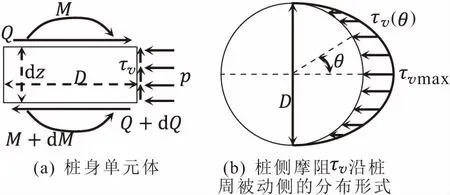
图2 大直径桩身单元体受力图Fig.2 Force analysis diagram of large diameter pile element
如图2(a)所示,任取桩身长度为dz的单元体进行受力分析,其中Q、Q+dQ和M、M+dM分别为单元体上下界面承受的剪力(kN)和弯矩(kN·m)。由水平方向力的平衡,可得:
Q=Q+dQ+pdz
(1)
如图2(b)所示,Ashour等[11]和李洪江等[7]指出,桩侧摩阻τv沿单元体被动侧截面的分布服从余弦函数,在截面θ=0处为最大值τvmax,随着角度θ的增大而减小,在θ=±π/2处趋于0。截面任一角度θ处桩侧摩阻τv(θ)可由公式τ(θ)=τvmaxcosθ计算。考虑桩侧摩阻对桩身截面弯矩的影响,由图2(a)中桩身单元体的弯矩平衡,对单元体下界面中心求矩,可得:
(2)
公式右边的第二项即表示由桩侧摩阻τv产生的抵抗弯矩Mr(kN·m),令:
(3)
略去公式(2)中的高阶小量,并结合梁的弯曲公式和公式(1),可得到桩身侧向位移的微分控制方程如下:
(4)
式中:EI为桩身抗弯刚度(kN·m2);k为桩侧径向地基土反力模量(kN/m2),k=p/y。
目前确定k值的方法有许多,其中m法[2]等线性方法便于计算,但其仅适用于桩身发生小变形的情况,无法考虑桩侧土的非线性特点;p-y曲线法[4]虽可反映地基土的非线性特点,但求解较为繁琐;应变楔模型[5]通过分析桩-土三维相互作用,可将土体应力-应变关系与桩身位移-土反力关系联系起来,既能反映土体的非线性特点,且计算又较为方便,故本文利用应变楔模型计算k值。
1.2 改进的应变楔模型
应变楔模型最初由Norris等[5]提出,后经杨晓峰等[12]、Xu等[13]发展,将桩身线性位移假设修正为桩身非线性位移假设,但是所建立的修正应变楔模型仅适用于长径比较大(桩径较小)的桩基,仅将桩身位移零点上部被动侧土体视为楔形受压区,以此确定桩身上部楔形土体的k值,桩身下部土体的k值仍通过m法确定。但对于大直径桩基而言,桩身抗弯刚度较大,桩身下部也将产生位移(见图1)。因此,本文将大直径桩基的下部桩侧土体也视为楔形受压区,将杨晓峰等[12]建立的修正应变楔模型进行了改进,推广至大直径桩基水平承载力分析中。
如图3所示,桩侧被动受压区土体被简化为三维楔形体,对于桩基础埋深z处楔形土体水平截面有如下受力平衡表达式,从而建立了桩侧径向地基土反力p与楔形土体应力值之间的联系[5]:
p=S1BCΔσh+2S2Dτh
(5)
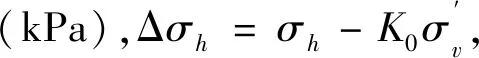

图3 改进的应变楔模型几何形状Fig.3 Geometry of modified strain wedge model
(6)
式中:φm为桩侧土体的内摩擦角发挥值(°),与土体的应力状态相关;τhf为桩侧极限水平剪应力(MPa);φ为土体的峰值内摩擦角(°)。
三维楔形体几何大小与桩基受荷水平相关,并呈动态变化,在达到极限承载状态前的任一荷载水平作用下,楔形土体的动态底角βm(°)由下式确定[5]:
βm=45+φm/2
(7)
地基埋深z处楔形土体前置宽度BC可由下式确定:
(8)
式中:Z0为桩身侧向位移为零位置对应的地基埋深(m)。
如图4所示,假设桩身位移在基础埋深范围内呈非线性变化,并引入邓肯-张模型[16]描述楔形土体的应力-应变状态。同时,为了方便后面计算,结合有限差分法,将桩体与楔形土体进行均匀离散,离散长度为h,埋深段桩长为Lb,在其范围内桩体与土体离散层数为mLb=Lb/h。依据差分原理、邓肯-张模型和土体应变莫尔圆原理,任一荷载作用下离散点i处桩身位移yi、桩段i的转角δi与对应土层i的内摩擦角发挥值φmi、水平应力增量Δσhi、应变εi的关系式如下:
(9)
(10)
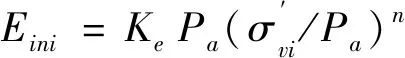
根据土体应力发挥水平,由下式可确定土层i的内摩擦角发挥值φmi[5]:
(11)
楔形土体内桩侧径向地基土反力极限值pui(kN/m)可由下式计算:
pui=S1BCΔσhfi+2S2Dτhfi
(12)

图4 改进的应变楔模型和桩身差分化Fig.4 Modified strain wedge model and discretion of the pile
1.3 桩侧摩阻τv、桩端弯矩Mb和桩端剪力Qb的计算
桩身在侧向位移过程中,由于土体径向土压力与接触位移的作用,桩-土接触面会产生切向摩擦力,因此桩侧摩阻τv与土体径向压应力相关,由应变楔模型可确定土体径向压应力峰值σNmax(kPa):
σNmax=S1BCΔσh/D+γ′z
(13)
进一步地,类似于公式(6),桩-土接触面的桩侧摩阻最大值τvmax可由下式计算:
τvmax=2σNmaxtanφm≤σNmaxtanφ
(14)
式中:φm与土体应力水平有关,通过φm可以反映桩侧摩阻最大值τvmax与土体径向压应力峰值σNmax的动态变化关系,将公式(14)代入公式(3)即可确定桩侧摩阻引起的抵抗弯矩。Borden等[14]认为在计算大直径桩基水平承载力时需要考虑桩端抵抗弯矩Mb和桩端水平剪力Qb的影响,关于桩端弯矩Mb的计算,可根据下式确定:
Mb=kbMδmLb
(15)
式中:δmLb为桩端转角(rad);kbM为桩端弯矩计算刚度(kN·m),相应规范[17]中规定kbM可由公式kbM=kνIb计算,其中kν为桩端土体竖向反力系数(kN/m3),kν=max{mLb,10m}[m为径向地基反力比例系数(kN/m4),可根据相关规范确定[2];Lb为桩基的埋深段桩长(m)];Ib为桩底截面的惯性矩(m4),Ib=πD4/64。
Gerolymos等[10]认为桩端弯矩Mb存在极限值Mbu,竺明星等[15]根据桩端土应力分布规律确定了桩端弯矩极限值Mbu(kN·m)的计算公式如下:
Mbu=πD3qbu/24
(16)
式中:qbu为桩端土单位面积极限承载力(kN/m2),可根据相应规范确定[2]。
此外,Gerolymos等[10]在研究箱型基础水平承载能力时建议按下式计算桩端土体水平剪力Qb:
Qb=kbQymLb
(17)
式中:ymLb为桩端土体侧向位移(m);kbQ为桩端土体水平剪力计算刚度(kN/m),可由公式kbQ=2EsD/[(2-ν)(1+ν)]计算,其中Es为桩端土体弹性模量(kPa)。
本文基于公式(17)计算桩端土体水平剪力Qb,并考虑其极限值Qbu(kN),由下式计算桩端剪力极限值Qbu:
式中:A为桩端截面面积(m2)。
1.4 计算流程
桩端弯矩和桩端剪力对大直径桩基水平响应的影响可通过桩端的边界条件进行考虑,由公式(15)和(17)可得桩底的边界条件为
MmLb=Mb,QmLb=Qb
(18)
式中:MmLb和QmLb分别为桩底离散节点mLb处的弯矩(kN·m)和剪力(kN)。
桩顶自由时,桩顶边界条件为
M0=Mt,Q0=Pt
(19)
式中:M0和Q0分别为桩身泥面处离散节点0处的弯矩(kN·m)和剪力(kN)。
采用有限差分法对方程(4)进行求解,由图4所示,根据差分式与微分式的关系,结合桩基两端边界条件[见公式(18)、(19)],可将桩身所有离散节点的位移方程(4)转化为差分方程组:
[K][Y]=[P]
(20)
式中:[K]为(mLb+1)×(mLb+1)阶桩身刚度矩阵;[Y]与[P]分别为(mLb+1)×1阶桩身侧向位移矩阵和水平荷载矩阵。
通过求解差分方程组(20),即可得到桩身侧向位移矩阵[Y],差分法的具体计算步骤可参考文献[18]。
综上所述,利用改进的应变楔模型,考虑桩侧摩阻、桩端弯矩和桩端剪力影响的大直径桩基水平承载力分析方法的计算流程图见图5,据此本文编制了MATLAB求解程序。图5中,初值矩阵[Y0]可按式[K0][Y0]=[P]计算,其中[K0]可按m法确定。值得注意的是,若采用p-y曲线法计算k值,则差分方程组(20)将变为复杂的非线性方程组,求解较为繁琐,而当采用应变楔模型时,可将差分方程组(20)转化为线性方程组,方便计算,这也体现了应变楔模型的计算优势。
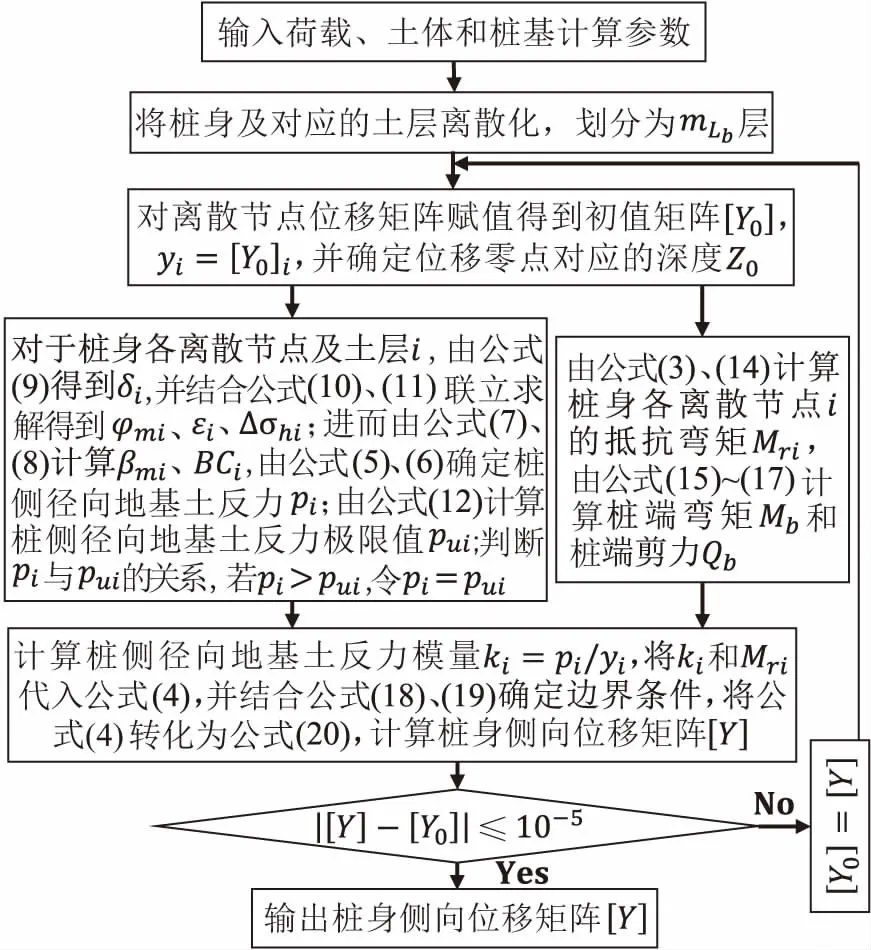
图5 基于改进应变楔模型的大直径桩基水平承载力分析方法的计算流程图Fig.5 Flow chart of calculation procedure of the horizontal bearing capacity analysis method for large diameter pile base based on modified strain wedge model
2 算例验证与影响程度分析
2.1 算例验证
Bhushan等[19]开展了7根钻孔灌注桩的现场水平荷载试验,试验桩分别位于3个地基土性质不同的场地中。其中,1~3号桩位于场地A,水平荷载施加在距泥面0.38 m处;4~5号桩位于场地B,6、7号水平桩位于场地C,水平荷载作用点均在泥面处。由于1~3号桩为扩底桩,故本文仅对4、5号桩和6、7号桩进行大直径桩基水平承载力计算。场地B地基土为成层砂土,深度0~0.9 m为粉砂,深度0.9~5.5 m为泥质粉砂,土体密实度分别为77%和88%,土体重度均为16.5 kN/m3;场地C地基土也为成层砂土,深度0~1.8 m为粉砂,深度1.8~5.5 m为泥质粉砂,土体密实度分别为38%和92%,土体重度均为16.5 kN/m3。4、5号桩的桩径分别为0.61 m和0.91 m,抗弯刚度EI分别为1.53×105kN·m2和7.6×105kN·m2;6、7号桩的桩径分别为0.91 m和1.22 m,抗弯刚度EI分别为7.6×105kN·m2和2.45×106kN·m2。上述试桩埋置深度均为5.5m。
本文采用上述建立的基于改进的应变楔模型,
利用考虑桩侧摩阻τv、桩端弯矩Mb和桩端剪力Qb影响的大直径桩基水平承载力分析方法,计算了上述4组试桩桩身泥面处的水平荷载-位移曲线,并与现场试验的实测结果以及不考虑上述因素影响的传统应变楔方法的计算结果进行了对比,其结果见图6。

图6 不同试桩桩身泥面处水平荷载-位移曲线Fig.6 Load-displacement curves at the mud surface of different test piles
经计算,4号桩的相对桩长Lb/LT>4,属于弹性长桩范围,5~7号桩的相对桩长则为4>Lb/LT>2.5,属于中短桩,其中LT=(EI/mb0)0.2[b0为计算桩径(m)][2]。弹性长桩桩身下部水平位移接近于0,因此对于4号桩基水平承载力的计算,则不考虑桩端弯矩和桩端剪力的影响,仅考虑桩侧摩阻的影响。依据地基土性质,经试算确定上述计算过程中场地B和C的桩端土单位面积极限承载力qbu的取值均为1 200 kN/m2,土体弹性模量Es的取值均为40 000 kPa,其余的计算参数见表1。
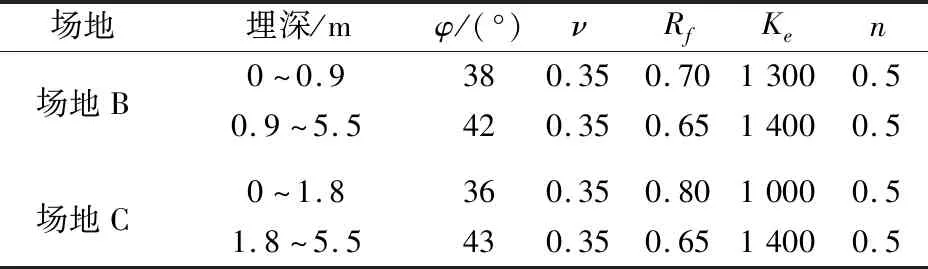
表1 场地B和C土体计算参数Table 1 Computed parameters of the soil of site B and C
由图6可见,当完全考虑桩侧摩阻τv、桩端弯矩Mb和桩端剪力Qb的影响时,本文计算结果与实测结果较为一致,证明了本文建立的大直径桩基水平承载力计算方法的准确性;而当不考虑上述因素,按传统的应变楔模型进行计算时,其计算结果对比实测值偏于保守的程度较大,当逐渐增加考虑τv、Qb和Mb的影响时,其计算结果也越来越接近实测值,因此τv、Mb和Qb对大直径桩基水平承载力的发挥起到有利的作用。较传统的分析方法,本文方法能更充分考虑地基土体承载力的发挥水平。
另外,由图6还可以看出,对于同一试桩,当荷载较小、桩身发生小位移时,是否考虑上述因素影响的计算结果差别不大,而随着水平荷载的增大,不考虑上述因素的计算结果偏于保守的程度显著增加;当横向对比4组试桩时,这一保守程度也随着桩径的增加而增大。因此,上述因素对桩基水平承载能力的影响程度除了与荷载大小相关以外,还与桩基直径有密切联系,这反映了桩基尺寸效应的作用。为了进一步分析桩基尺寸效应,下面分别开展了不同桩基尺寸下τv、Mb及Qb对桩基水平承载能力的影响程度研究。
2.2 桩侧摩阻τv、桩端弯矩Mb和桩端剪切Qb对桩基水平承载能力的影响程度分析
按上述算例中场地C中的地基条件,采用本文方法对地基埋深均为5.5 m,桩身土体弹性模量E均为2.26×107kPa,桩径分别为0.20 m、0.40 m、0.61 m、0.91 m、1.22 m和1.50 m的桩基水平承载力进行了计算,若以桩身泥面处位移20 mm为极限值,则可以计算得到不同桩径下桩基的极限水平荷载Pu,见表2。
由表2可知,随着桩径的增加,桩基的极限承载能力也随之变大(即桩基尺寸效应)。究其原因,除了桩径增加以致桩身截面抗弯刚度提高的影响外,τv、Mb和Qb对桩基尺寸效应的发挥也有相应的影响(见图6)。据此,本文将分析上述各个因素对桩基水平承载能力的影响程度。
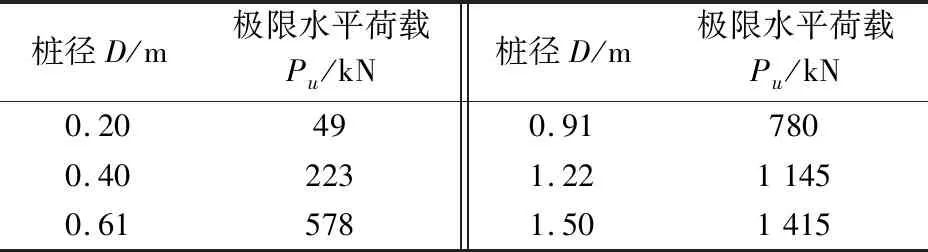
表2 桩基极限水平荷载与桩径的关系Table 2 Relationship between pile ultimate load and pile diameter
结合公式(3),对公式(2)中的弯矩平衡式沿桩长z进行积分,可以得到下式:
(21)
式中:M(z)为桩身总弯矩(kN·m);Mrc(z)为桩身累积抵抗弯矩(kN·m),即抵抗弯矩Mr沿桩长的累积,反映了桩侧摩阻τv对水平受荷桩弯矩的影响;MQ(z)为桩身剪力弯矩(kN·m),由桩身内部剪力Q所形成。
图7为桩身弯矩的分布规律。其中,图7(a)为MQ(z)、Mrc(z)和总弯矩M(z)随桩埋深的变化规律;图7(b)为Mrc(z)随荷载的变化规律。由图7(a)可见,桩身累积抵抗弯矩Mrc(z)沿着桩埋深的增加逐渐累积增加,至桩底处达到最大值;桩身剪力弯矩MQ(z)与桩身总弯矩M(z)的分布规律类似,桩侧摩阻所形成的抵抗弯矩Mr可以抑制MQ(z)的发展;桩身总弯矩M(z)因为Mrc(z)的存在而减小。由图7(b)可见,随着水平荷载的增加,桩身累积抵抗弯矩Mrc(z)随之增加。

图7 桩身弯矩的分布规律Fig.7 Distribution law of pile bending moment
因此,基于桩身累积抵抗弯矩的形成原因、分布特点,本文使用桩身底部累积抵抗弯矩最大值Mrcmax(kN·m)来衡量桩侧摩阻τv对水平受荷桩承载能力的影响。
不同桩径下,τv、Mb和Qb随荷载水平(Pt/Pu)的变化情况,以及分别单独考虑桩侧摩阻τv、桩端弯矩Mb和桩端剪力Qb相较于不考虑上述各个因素影响时桩身泥面处侧向水平位移的降低幅度Δys(%)随荷载水平的变化情况,见图8。
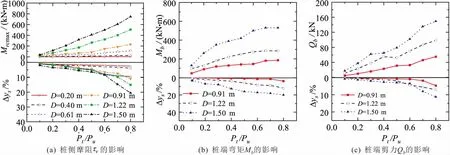
图8 不同桩径下τv、Mb和Qb对桩基水平承载能力的影响Fig.8 Influence of τv、Mb and Qb on horizontal bearing capacity of pile foundation with different pile diameters
由图8(a)可见,对于桩侧摩阻τv来说,当桩径较小时(D=0.20 m)时,Mrcmax值趋近于零,侧向水平位移的降低幅度Δys也很小,此时计算桩的水平响应时可不考虑τv的影响;而当桩径较大(D≥0.40 m)时,Mrcmax值以及侧向水平位移的降低幅度Δys随荷载水平的增大而增大,且增加幅度随着桩径的增加而明显增大,此时在计算大直径桩基水平承载力时不可忽略τv的影响。由图8(b)、(c)可见,对于桩端弯矩、桩端剪力来说,随着荷载水平和桩径的增加,Mb和Qb值也随之增加,对侧向水平位移的降低幅度Δys也呈现出类似的发展趋势。图8中Δys反映了上述各个因素对于大直径桩基水平承载能力的提升程度。通过横向对比图8(a)、(b)和(c)可见,τv、Mb和Qb对大直径桩基水平承载能力呈现出不同程度的有利作用,当工况为桩径D=1.50 m、Pt=0.8Pu时,桩侧摩阻τv的影响(约22%)较桩端弯矩Mb(约20%)的稍大,桩端剪力Qb的影响(约11.5%)最小,因此对于大直径桩基水平承载力的计算不能仅考虑τv的影响,Mb和Qb的影响也不可忽视;上述各个因素对大直径桩基水平承载能力的影响程度均随着桩径的增加而增大,桩基水平承载能力随桩径的提高(即桩基尺寸效应)不仅是由于桩身抗弯刚度的增大,τv、Mb和Qb也发挥了相应的有利作用,因此除桩身抗弯刚度外,桩基尺寸效应是τv、Mb和Qb共同作用的结果。由此可见,对于大直径桩基水平承载力的计算,十分有必要考虑上述各个因素的影响。
3 结 论
(1) 基于改进的应变楔模型,提出了一种考虑桩侧摩阻、桩端弯矩和桩端剪力的大直径桩基水平承载力的计算分析方法,并通过与现场试验的实测结果进行对比,验证了本文方法的准确性。
(2) 桩侧摩阻、桩端弯矩和桩端剪力对大直径桩身水平承载能力的发挥起到了有利的作用,不考虑上述因素时,计算结果偏于保守,保守程度随桩径和荷载水平的增大而增加。
(3) 按形成原因,桩身弯矩分布可以拆分为桩身累积抵抗弯矩和桩身剪力弯矩两部分,桩身总弯矩因为桩身累积抵抗弯矩的存在而减小。
(4) 除桩身抗弯刚度外,桩基尺寸效应是桩侧摩阻、桩端剪力和桩端弯矩3个因素共同作用的结果,各个因素的影响程度与桩径的相关性较大,且桩侧摩阻的影响最大,桩端弯矩次之,桩端剪力的影响最小,对于大直径桩基水平承载力的计算,建议采用本文方法综合考虑上述各个因素的影响。
