运用水热运移模拟定量评价地表水与地下水的转化
2020-06-29卢昱含靳孟贵白宏伟刘亚磊刘延锋
卢昱含,鲜 阳,靳孟贵,白宏伟,刘亚磊,刘延锋
(1.中国地质大学(武汉)盆地水文过程与湿地生态恢复学术创新基地,湖北 武汉 430074;2.中国地质大学(武汉)环境学院,湖北 武汉 430074;3.中国地质调查局武汉地质调查中心,湖北 武汉 430205)
地表水与地下水联系紧密,两者之间的相互作用与转化关系复杂,密切影响着潜流带水分、物质与能量的交换过程[1-3]。因此,研究地表水与地下水的相互作用对于水资源评价、水资源开发管理、水污染防治和生态系统保护均具有重要的意义[4-5]。
干旱地区人类活动引起的土地利用和渠系渗漏的变化对地表水与地下水相互作用的影响强烈,而引水灌溉的渠道入渗是干旱地区地表水与地下水相互作用的主要形式[6]。近年来,干旱地区地表水与地下水的相互作用研究受到国内外研究机构的广泛重视[7-8]。干旱地区水资源开发利用与调度配置的关键和基础是判定河流和渠道与地下水的转化关系,量化两者间的转化量及其时空变化规律[9]。
干旱地区浅层地下水水温相对恒定,而河流等地表水水温受气温的影响,一般具有较为明显的季节性变化和日变化规律,地表水与地下水发生相互作用的过程中,潜流带温度场会发生明显的变化[10-12]。近年来,随着温度场与渗流场耦合研究的深入、温度数据监测成本的降低[13]以及多孔介质水热耦合运移模拟软件的大量开发,运用水热运移数值模拟定量评价地表水与地下水相互转化关系的研究有了较大的发展。如Su等[14]和Constantz[15]利用VS2DHI软件模拟了河岸剖面二维温度场,并结合观测井中监测的季节性地下水温度估算了含水层的水力传导系数和地表水与地下水的相互转化速率;任杰等[16]和潘维艳等[9]利用水热运移模拟分别研究了大坝与农渠的渗漏问题;Ju等[17]结合沙箱试验与数值模拟,分别采用实测温度、水头数据分析评价了数值模拟结果,结果表明水头与温度数据结合可提高渗流模拟结果的可信度和精度。但目前针对干旱渠道水文动态剧烈变化条件下渠道地表水与地下水相互转化关系和转化水量的时空变化规律方面的研究成果较少,且转化量评价存在很大的不确定性。
本文以新疆玛纳斯河流域炮台镇附近头道沟渠道的排水干渠作为研究对象,通过野外原位试验实时监测渠道横断面地下水温度、地下水水位、渠道地表水水位和不同埋深处河床沉积物的温度变化,分析地表水与地下水相互转化关系变化前后温度的规律特征,并建立二维均质多孔介质变饱和土壤水热运移耦合数值模型,模拟了渠道附近地下水的水热运移,反演土壤饱和水力参数,定量计算渠道地表水与地下水的转换量,为渠道渗漏定量估算和地表水与地下水联合调度提供参考。
1 研究区域概况
玛纳斯河流域位于新疆天山北麓中段、准噶尔盆地南缘,地处北纬43°27′~45°21′、东经85°01′~86°32′,地势自东南向西北缓缓倾斜。流域由东向西分别由塔西河、玛纳斯河、宁家河、金沟河、巴音沟河以及相连的五片冲积平原组成。从南向北地貌具有明显的分带性,可以划分为5个地貌带:山地带、山前褶皱丘陵带、串珠状冲积扇带、平原曲流带、玛纳斯河尾闾湖泊和沙漠。
流域属典型的干旱内陆盆地气候,冬冷夏热,年(日)温差大,光照充足,蒸发强烈[18]。该流域年平均气温为9.1℃;年平均降水量为110~200 mm,降水分布不均,垂直分带特征明显,主要集中在5~8月份,约占年降雨量的67%;年均蒸发量为1 500~2 000 mm[19]。流域地表水补给主要来自于降水及冰川融化,地下水补给主要来自于通过河流的垂直渗透、渠道渗漏、灌溉回灌、山前侧向地下水补给[20-21]。该地区平原区地表水与地下水的相互作用同时受到自然条件和人类活动的影响,两者之间的关系极为复杂。
头道沟渠道的排水干渠位于炮台镇附近(N44°45′~44°50′,E85°30′~85°35′),地处平原灌溉区,见图1。

图1 研究区地理位置Fig.1 Location of the research area
根据研究区左右岸2m深钻孔的土壤岩性数据,对比白宏伟等[22]对玛纳斯河流域二维岩性结构剖面的研究成果,认为研究区土壤质地分布较为均一,大部分为粉质壤土,受渠道及气候的影响,入渗水水温较低,低温水入渗形成的温度变化信号较为明显。头道沟渠道兼顾排水与灌溉功能,每年4月初上游开始向渠道放水,9月底停止供水,渠道地表水水位呈现规律性的升降变化。
2 研究方法
2.1 温度和水位监测
头道沟渠道属未衬砌的典型农渠,本研究选定垂直头道沟渠道的断面,测定渠道断面几何形态,并布置监测井、水位和温度传感器。将监测井G1底部以下3.94 m处水平线定为基准线,头道沟渠道监测断面和监测井布置见图2。
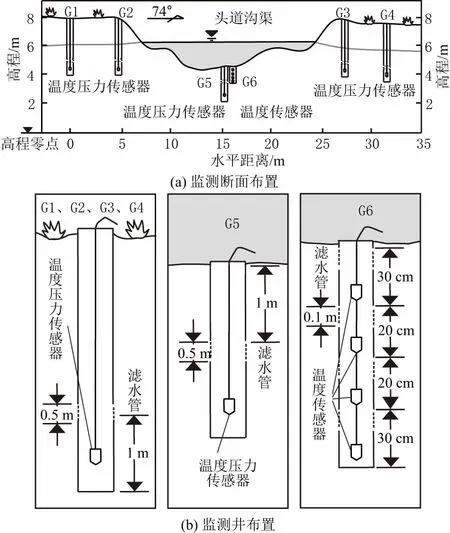
图2 头道沟渠道监测断面和监测井布置Fig.2 Layout of the monitoring cross sections and wells of Toudaogou canal
监测井管为4 m长的PVC管,滤水管长为0.5 m。河岸监测井(G1、G2、G3、G4)的滤水管布置在监测井底部以上1 m处,每个监测井内均布置一个Solinst Solinst Levelogger 2参数探头(压力、温度)自计水位和温度。水位测量精度为±0.05 m,分辨率为0.001 m;温度测量精度为±0.2℃,分辨率为0.01℃。
河床监测井(G5、G6)的滤水管位于河床下1 m处,其中监测井G5内布置一个Solinst Levelogger 2参数探头自计水位和温度;监测井G6内布置一个HOBO温度记录仪记录30 cm、50 cm、70 cm、100 cm埋深处河床沉积物的温度。水位测量精度为±0.05 m,分辨率为0.001;温度测量精度为±0.2℃,分辨率为0.02℃。
除图示监测井外,另布置一个Solinst Levelogger 2参数探头监测渠道地表水水位和温度,并使用数据采集仪记录各测点的温度和水位,采集时间间隔为15 min,自2015年7月27日22∶00至9月2日22∶00连续监测。
2.2 水文地质概念模型
由于模型水力参数受河床沉积物岩性结构和饱和度变化的影响可能会呈现几个数量级的变化[10],单纯依靠水位校正数值模型会使得模型水力参数率定存在较大的不确定性,而热传导系数的变化范围较小。因此,本文通过建立水热运移耦合模型,利用水头和温度数据约束和校正模型水力参数,以降低模型的不确定性。
地表水与地下水相互作用时,土壤中水分运移与热量传输会产生相互影响,土壤中水分运移会引起土壤的体积热容量和热传导系数的变化,改变热量传输与交换,进而改变土壤中温度的分布。由于两者之间的耦合作用过程非常复杂,为了研究渠道地表水与地下水的水热运移规律,可忽略温度变化引起水的性质变化,将监测断面概化为二维均质多孔介质变饱和水热运移耦合模型。
以头道沟渠道断面形态为上边界,以监测井G1埋深10.06 m处水平线为底边界,模型深度约为10 m;以监测井G1、G4为模型左、右边界,模型水平长度为31.56 m。建立的头道沟渠道研究断面水文地质概念模型,见图3。
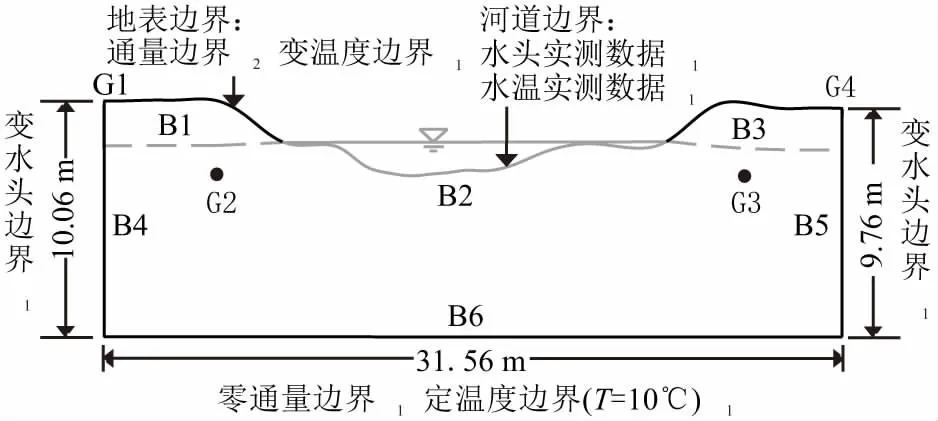
图3 头道沟渠道研究断面水文地质概念模型Fig.3 Conceptual hydrogeological model of the research cross section of Toudaogou canal
渗流场边界条件:地表边界B1、B3为通量边界 (Neumann边界),监测期间几乎无降雨,边界赋值为结合经验公式和实测水面蒸发E0数据计算出的边界蒸发通量,由付秋萍等[23]研究可知,清华大学雷氏公式在新疆地区具有广泛的适用性,参考该研究中粉壤土参数拟合成果,以函数形式赋值输入;渠道边界B2为已知变水头边界,输入实测渠中水位值(Dirichlet边界);左右边界B4、B5为已知变水头边界,分别输入井孔G1、G4的实测水头值(Dirichlet边界);底边界B6为隔水边界(Neumann边界)。初始条件为实测压力水头数据的线性插值。
温度场的边界条件:地表边界B1、B3为变温度边界,实测日平均气温数据(Dirichlet边界);渠道边界B2为变温度边界,输入实测渠道水温数据(Dirichlet边界);底边界B6为定温度边界,T=10℃(Dirichlet边界)。初始条件为实测温度数据的线性插值。
2.3 数学模型
2.3.1 土壤水分运动方程
假定研究断面土壤为均质各向同性,设z轴垂直向上,x轴水平向右,二维均质各向同性土壤水分运动的偏微分方程及其定解条件可表示如下:
(1)
式中:t为时间变量(s);x、z均为空间坐标(m);h(x,z,t)为压力水头(m);c(h)为比水容量,c(h)=∂/∂h;K(h)为非饱和土壤水力传导系数(m/d),是h的函数;h0(x,z)为渗流场初始地下水水位(m);h1(x,z)为第一类边界Γ1水位值(m);ε(x,z,t)为第二类边界Γ2通量(地表蒸发量)(m/d);Ω为渗流区域。
2.3.2 土壤热运移方程
采用热传导和对流方程来表征土壤热运移过程,忽略气态水扩散,仅考虑液态水的运动对土壤热量传输的影响,二维均质多孔介质变饱和土壤的热运移偏微分方程及其定解条件可表示如下:
(2)

2.3.3 土壤水力参数
土壤含水率θ、土壤有效饱和度Se、非饱和土壤水力传导系数K这些参数均随着压力水头h的变化而发生改变,需要通过数学模型来表征它们的本构关系。本文选用Mualem-van Genuchten公式[24]进行描述,具体公式可表示如下:
(3)
(4)
(5)
式中:θr为土壤残余体积含水率(m3/m3);n、m和α为经验拟合参数,其中m=1-1/n,α为受土壤物理性质影响的参数(1/m);l为经验拟合参数,通常取平均值0.5;Se为土壤有效饱和度;Ks为土壤饱和水力传导系数(m/d)。
2.4 数值模型建立与参数识别
采用地下水数值模拟软件FEFLOW建立二维均质多孔介质变饱和土壤水热运移耦合数值模型。使用advancing front剖分网格,得到总网格数为3 178、节点数为1 683。设定边界条件,并设置土壤水力参数和土壤介质热特性参数初值,采用自动时间步长划分离散时间,使用线性插值结果作为变饱和土壤非稳定渗流场和温度场的初始值。
数值模拟采用的土壤水力学参数:在距离监测井G2和G3正北1 m处,钻孔采集0 cm、-30 cm、-50 cm、-70 cm、-100 cm、-130 cm、-150 cm、-170 cm、-200 cm深度处的土壤样品,采用中国地质大学(武汉)材料与化学分析测试中心的Mastersizer 3000E激光衍射粒度分析仪测定土壤的粒度组成,结果表明土壤的粒度组成主要为粉粒(51.8%)和砂粒(43.84%),并参考美国农业部土壤质地分类方法,将其定名为粉质壤土;环刀采集左右岸0 cm、-50 cm、-100 cm深度处土壤样品,测定土壤的干容重为1 650 kg/m3,利用Hydrus1D中内嵌的Rosetta Lite V1.1模块,使用土壤粒度组成和干容重数据确定初始土壤水力参数。
本次选用为期12 d(2015年7月27日22∶00至8月8日22∶00)的实测数据率定模型参数,使用水头和温度数据反演土壤水力参数,校正的模型参数见表1。
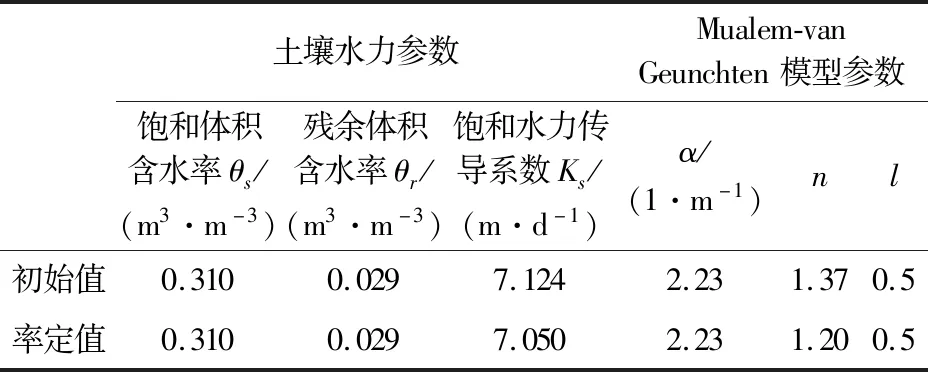
表1 反演的土壤水力参数Table 1 Inversed soil hydraulic parameters
数值模拟采用的土壤介质热特性参数有:干土的比热容Cs、干土的热导率λs、水的比热容Cw、水的热导率λw、土壤纵向热扩散度DL、土壤横向热扩散度DT。利用Lu等[25]研究模型中的常温土壤热导率公式计算干土热导率;参考Bridger等[26]和龙焘等[27]的研究成果设定干土比热容的数值;参考张盼盼[28]的研究数据设定土壤热运移的纵向扩散度和横向扩散度,土壤介质的热特性参数见表2。

表2 土壤介质的热特性参数Table 2 Soil thermal parameters
3 结果与讨论
保持率定后的模型参数不变,使用为期37 d(2015年7月27日22∶00至9月2日22∶00)的野外监测数据验证模型的可靠性。本文利用均方根误差RMSE和决定系数R2来评价模拟值与实测值的吻合程度,其计算公式如下:
(6)
(7)
不同埋深处河床沉积物温度模拟值与实测值的对比结果,见图4。
由图4可见,30 cm、50 cm、70 cm、100 cm埋深处河床沉积物温度模拟值与实测值的差异较小,总体趋势一致,且随着埋深的增加,温度波动的振幅减小;温度模拟值与实测值的总均方根误差RMSE为0.220,决定系数R2均大于0.95,认为河床沉积物温度梯度的模拟结果合理可靠。
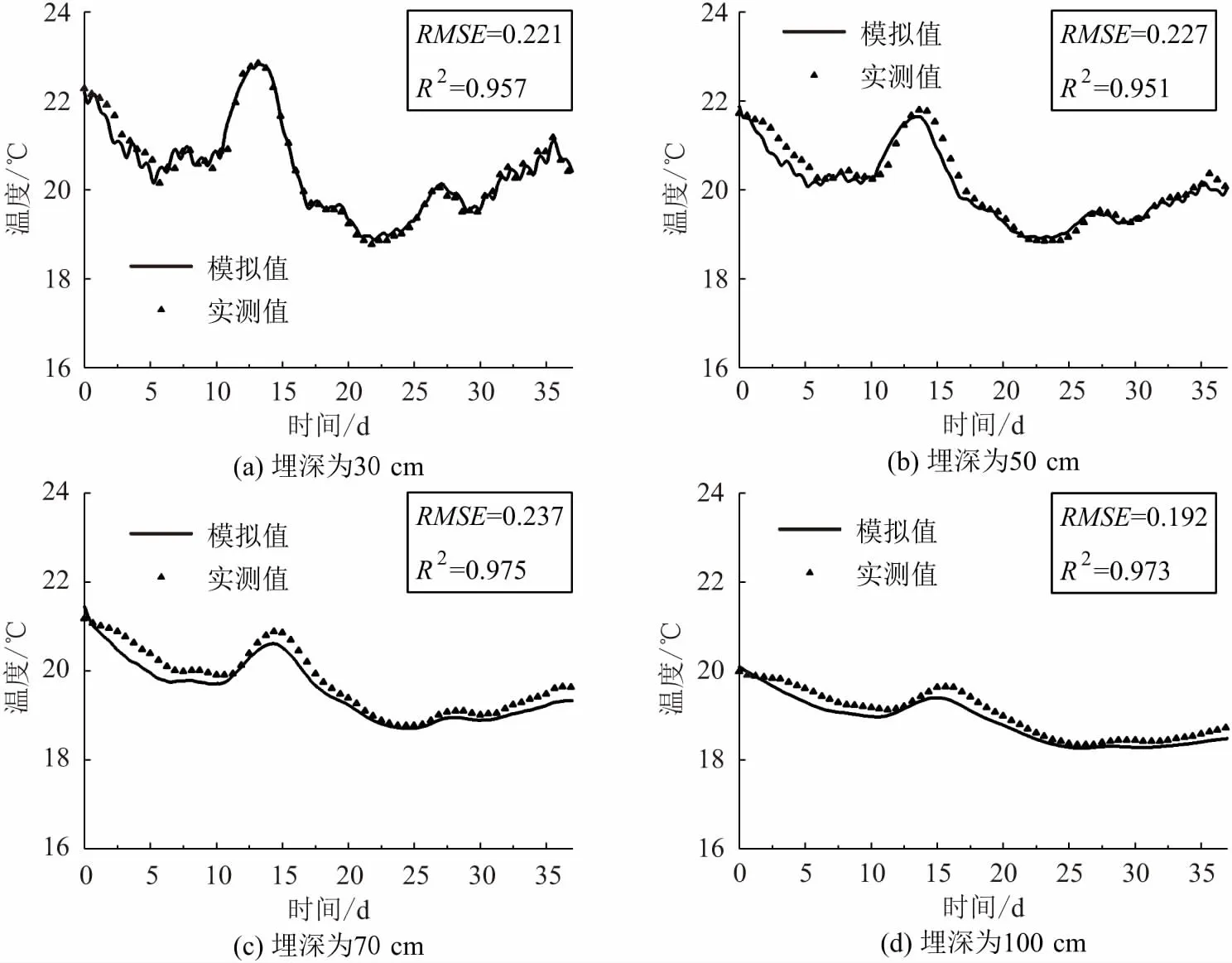
图4 不同埋深处河床沉积物温度模拟值与实测值的对比Fig.4 Comparisons between simulated and observed bed sediment temperature at different depths
河岸监测井G2、G3水头模拟值与实测值的对比结果,见图5。
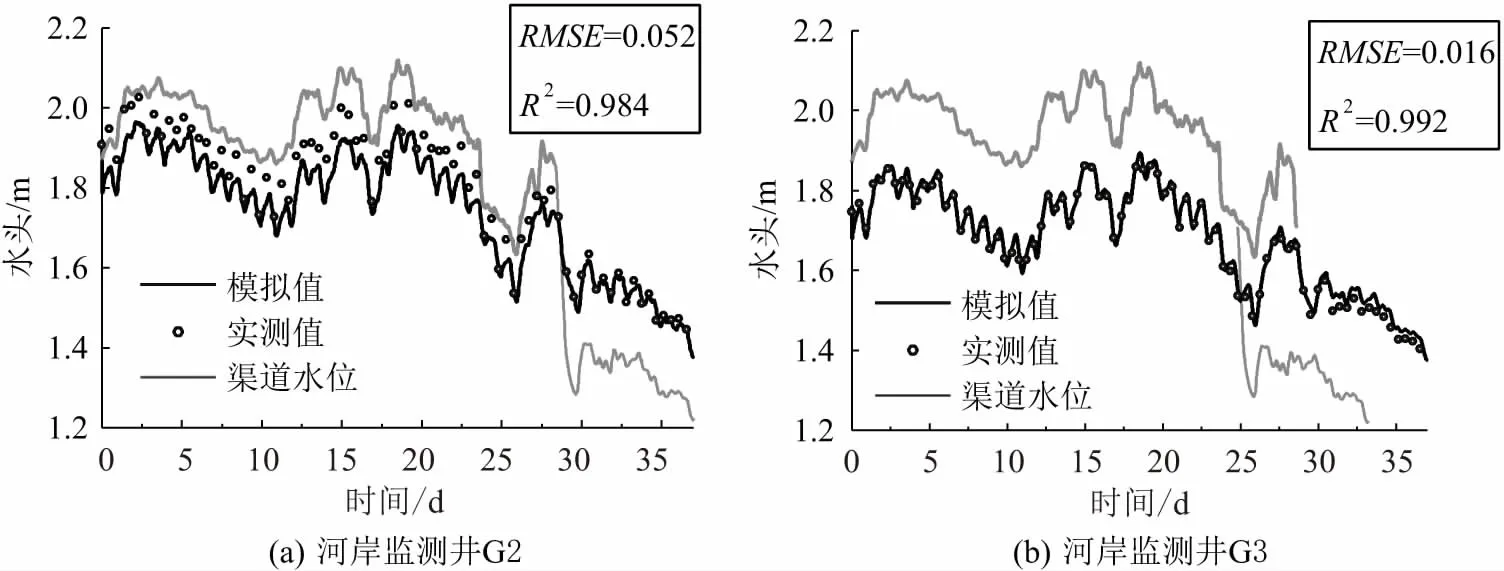
图5 河岸监测井G2、G3水头模拟值与实测值的对比Fig.5 Comparisons between simulated and observed hydraulic head for monitoring wells G2 and G3
由图5可见,尽管河岸监测井G2、G3处水头的模拟值与实测值在某些观测点上存在一定的误差,但总体趋势基本一致;水头模拟值与实测值的总均方根误差RMSE为0.033,决定系数R2均大于0.98,认为渗流场的模拟结果合理可靠,部分误差可能是由实际渠道断面土壤的空间变异性造成的。
河岸监测井G2、G3温度模拟值与实测值的对比结果,见图6。
由图6可见,河岸监测井G2、G3温度模拟值与实测值的差异较小,总体趋势一致;总均方根误差RMSE为0.115,决定系数R2均大于0.98,认为温度场的模拟结果合理可靠。
综上分析可见,研究区地温和水温的波动大,有明显的昼夜变化。渠道地表水与地下水相互作用时,渠道地表水的温度信号影响着河床沉积物的温度分布。本文针对不同埋深处河床沉积物的温度数据,提取其日周期波动的正弦函数拟合振幅值见图7。

图6 河岸监测井G2、G3温度模拟值与实测值的对比Fig.6 Comparison of simulated and monitored temperatures for monitoring wells G2 and G3
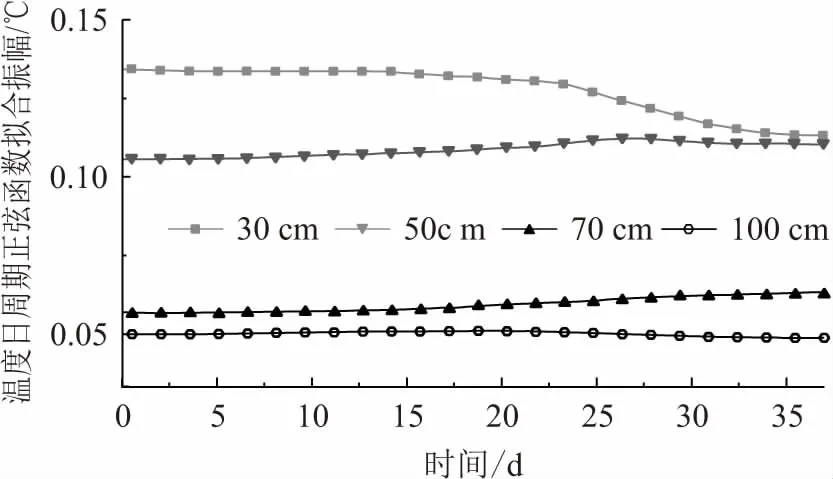
图7 不同埋深处河床沉积物温度曲线正弦函数拟合振幅Fig.7 Sinusoidal fitting amplitudes of bed sediment temperature curves at different depths
通过分析图4和图7可见,河床沉积物的平均温度从上至下逐渐降低,埋深小于30 cm处河床沉积物的温度受到渠道水温波动的影响较大,在埋深为50 cm及以下处河床沉积物的温度受渠道水温波动的影响不明显;当渠道地表水补给地下水时,渠道水温日周期波动信号向下传递,河床沉积物温度日周期波动的振幅(正弦函数拟合)随埋深增加而减小;当地下水补给渠道地表水时,低温地下水向上进行热量交换,缓冲了由渠道地表水引起的河床沉积物温度波动,50 cm埋深处河床沉积物的温度曲线信号随之变化,其日周期正弦波动的振幅减小。可见,通过分析50 cm埋深以上处河床沉积物的温度信号,即使在无水位数据的情况下,也能分析得出渠道地表水与地下水的相互作用关系。
为了研究渠道地表水与地下水的相互作用对渠道垂直剖面温度分布规律的影响,本文利用上述模拟结果,选取2015年8月12日22∶00、8月24日22∶00、8月25日22∶00、8月29日22∶00,即模拟时长分别为t=16 d、t=28 d、t=29 d和t=33 d 这4个不同时刻的温度场模拟结果,对比分析渠道地表水与地下水不同转化关系时,渠道研究断面的温度分布规律,见图8。
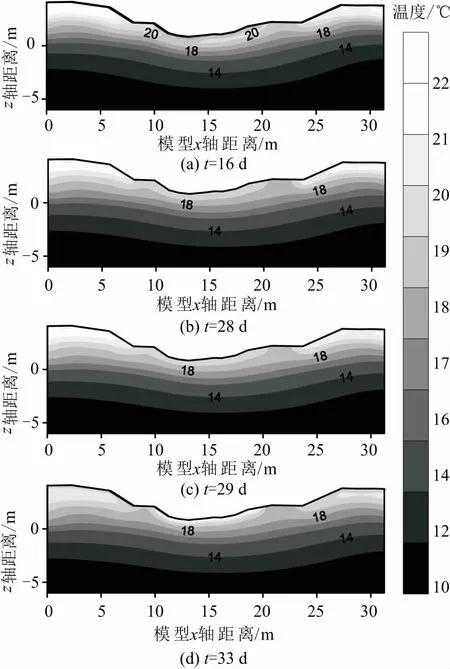
图8 不同时刻渠道研究断面的温度分布Fig.8 Distribution of temperature at the research cross section of the cannal at different times
由图8可见,渠道研究断面的温度分布由下至上大致可以分为低温区(10~17℃)、中温区(17~20℃)和高温区(20~23℃)。其中,低温区分布较为稳定,无论断面是渠道地表水补给地下水还是地下水补给渠道地表水,低温区的面积变化不大;高温区分布于受气温、水温影响较大的浅部非饱和层,其分布范围较小,面积变化差异大;中温区位于两者之间,受到渠道地表水与地下水相互作用中热传导作用的影响。
当渠道地表水补给地下水时,受温度日变异性大的渠道地表水入渗的影响,中温区的温度梯度整体随埋深的增加而逐渐增大,但局部的温度梯度方向可能相反;当地下水补给渠道地表水时,中温区的温度梯度方向一致,随着埋深的增加中温区的温度梯度逐渐减小。这在一定程度上表征了渠道研究断面渠道地表水与地下水的相互作用关系。
为了定量评价渠道地表水与地下水的转化水量,本文选取渠道边界单元,绘制出渠道研究断面单位长度累计入渗量的变化曲线,见图9。

图9 渠道研究断面单位长度累计入渗量的变化曲线Fig.9 Cumulative recharge per unit length of the research cross section of the canal
由图9可见,0~28.6 d内渠道研究断面单位长度累计入渗量随时间增大,渠道地表水补给地下水,随着渠道地表水水位的降低,渠道研究断面单位长度累计入渗量曲线斜率减小;28.6~37 d内渠道研究断面单位长度累计入渗量随时间减小,渠道地表水水位低于地下水水位,转化为地下水向渠道排泄,随着地下水水位的降低,渠道单位长度累计入渗量曲线斜率的绝对值减小。0~28.6 d内渠道单位长度累计入渗量为35.3 m2/d;28.6~37 d内渠道研究断面单位长度累计排泄量为9.626 m2/d;37 d内渠道单位长度累计入渗量为25.674 m2/d。
假设渠道研究断面为典型断面,可利用渠道研究断面单位长度累计入渗量估算整个渠道地表水与地下水的转化量。已知研究区断面位于新疆石河子农八师玛纳斯河灌区头道沟渠道的排水干渠上,干渠全长为12.6 km,南北走向,垂直等高线分布,控制灌溉面积为2万hm2。通过分析得出:2015年7月27日22∶00至2015年8月25日12∶30,头道沟干渠渠道地表水入渗补给地下水,地表水入渗补给水量约为4.448×105m3,2015年8月25日12∶30至9月2日22∶00,头道沟干渠排泄地下水,地下水排泄水量约为1.213×105m3。
4 结 论
本文以新疆玛纳斯河流域炮台镇附近头道沟渠道的排水干渠为研究对象,通过野外原位试验实时监测渠道横断面地下水温度、地下水水位、渠道地表水水位和不同埋深处河流沉积物的温度变化,分析了渠道地表水与地下水相互转化关系变化前后温度的规律特征,并建立二维均质多孔介质变饱和土壤水热运移数值模型,模拟分析与计算了头道沟干渠渠道地表水与地下水的相互转化关系和转化量,并得到如下结论:
(1) 浅层河床沉积物(埋深为50 cm以上)的温度曲线可示踪表征渠道地表水与地下水的相互转化关系。在观测计算时段内,2015年7月27日22∶00至2015年8月25日12∶30,渠道地表水补给地下水,2015年8月25日12∶30至9月2日22∶00,地下水向渠道排泄。河床沉积物可大致分为低、中、高三个温区,当渠道水补给地下水时,受渠道地表水入渗的影响,中温区温度梯度随埋深的增加而逐渐增大,可能出现浅层沉积物温度低于深层沉积物温度的现象;当地下水向渠道排泄时,中温区温度梯度方向一致,随着埋深的增加温度梯度逐渐减小。河床沉积物的温度日周期波动振幅(正弦函数拟合)随着埋深的增加而减小,当渠道地表水补给地下水时,50 cm埋深处河床沉积物的温度日周期波动振幅随时间增大;当地下水向渠道排泄时,50 cm埋深处河床沉积物的温度日周期波动振幅随时间减小。
(2) 使用土壤水热运移耦合模型反演得到试验区土壤的饱和水力传导系数为7.05 m/d。使用监测数据验证模拟结果,温度模拟值与实测值的RMSE为0.220,决定系数R2均大于0.95,水头模拟值与实测值的RMSE为0.033,决定系数R2均大于0.98,模拟值和实测值之间具有较好的一致性,表明率定后的土壤水热运移模型能较好地仿真渠道地表水与地下水相互转化的动态变化规律。
(3) 渠道研究断面单位长度累计入渗量为35.3 m2/d,发生在2015年8月25日12∶30时,模拟结束时渠道研究断面单位长度累计入渗量为9.626 m2/d。2015年7月27日22∶00至2015年8月25日12∶30期间,头道沟干渠渠道地表水入渗补给地下水,12.6 km长渠道地表水入渗补给量约为4.448×105m3;2015年8月25日12∶30至9月2日22∶00期间,头道沟干渠排泄地下水,地下水排泄量约为1.213×105m3。
