船舶月池的阻力与流场特性及其改进型式

詹星宇，毛筱菲*，2

1 武汉理工大学交通学院，湖北武汉430063

2 武汉理工大学高性能舰船技术教育部重点实验室，湖北武汉430063

0 引 言

随着当前海洋资源的开发以及海上平台的建设，钻井船等各类工程船舶的运用日益增多。月池常设置于各类工程船舶船舯附近，由甲板直接通向海底，一方面方便作业设备的安装与使用，另一方面也可避免其遭受波浪的影响。池内流体的运动形式通常可划分为垂直方向上的活塞运动和水平方向上的晃荡运动；同时，还伴随着漩涡的运动和自由面的翻卷、破碎，甚至是甲板上浪与船体结构的振动。

关于月池相关问题的研究，除了聚焦于船舶在波浪中零速作业时月池对船舶运动的影响外，考虑船舶在迁移状态下池内流体运动对航行阻力性能的影响也至关重要。国内外不少学者通过模型试验及数值方法对由月池引起的阻力增加问题进行了研究，并对月池内的流动、压力分布以及船身周围兴波波型等进行了模拟分析［1-3］。部分学者假设月池振荡幅度与阻力增加成线性关系，结合试验结果，提出了活塞及晃荡振荡模态下的月池附加阻力预报模型［1，4］。由于月池的设置恶化了船舶的阻力性能，因此有必要对月池型式进行改进以降低月池增阻。月池减阻可以通过抑制外部激励对池内流体运动能量的获取和漩涡发展的作用，或是增加池内流体运动的阻尼耗散漩涡运动能量，来减小池内流体的振荡幅度［5］。还有部分学者通过改变相关尺寸参数，验证了设置阶梯平台、切角、阻尼板、栅格板以及更加复杂型式的月池对改善月池增阻的效果，以优化月池的型式［1，6-9］。

目前，有关月池及其改进型式的流动细节与阻力变化关系的研究较少，而月池内流体复杂的流动是其影响船舶阻力的主要因素，因此，有必要分析其非定常流动现象与增阻机理。计算流体动力学（CFD）数值方法能够准确计及流动粘性及自由液面的影响，直观地捕捉流场细节，本文将利用该方法模拟带月池船舶的静水航行，通过分析各阻力成分，得到月池对船舶阻力性能的影响，并详细剖析不同航速下流场的复杂流动现象，探究月池增阻的原因，同时以阶梯型月池和切角型月池为例，研究其在改善月池增阻与流场特性方面的效果。

1 数值方法与研究对象

1.1 控制方程与数值求解

采用RANS 方法模拟粘性不可压缩流场，流体微团满足以下连续性方程与动量方程：

式中：t 为时间；xi，xj为笛卡尔空间直角坐标系中的坐标轴方向；vi为不同坐标轴方向上的流体速度分量；p 为流体压强；ρ为流体密度；υ为运动黏性系数；Gi为流体体积力分量；为雷诺应力项，其下标i，j=1，2，3。求解上述流动控制方程时，基于SIMPLEC 算法，选取k-ε湍流模型，空间上采用二阶迎风格式，时间上采用隐式非定常格式离散求解。流场涉及气、液两相流动，采用流体体积（Volume of fluid，VOF）方法，通过网格单元内流体所占体积与单元总体积之比，定义单元的相态。

1.2 计算模型与网格划分

本文重点探究月池内部流体流动以及其对阻力性能的影响机理，为便于计算验证，研究对象选取为与常规钻井船尺度相近的KCS 船型，其模型与主尺度参数分别如图1 和表1 所示。

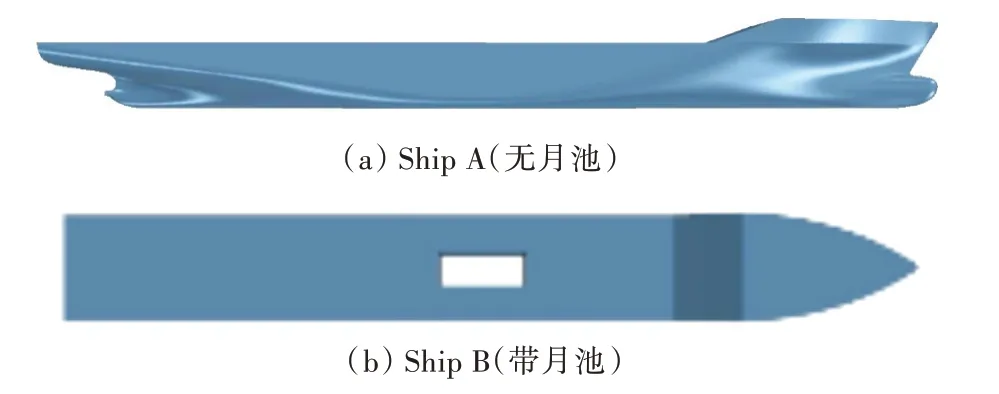
图1 KCS 模型Fig.1 KCS models

表1 船模主尺度Table 1 Main dimensions of the ship model

利用船型的对称性，使用半模型进行计算，图2 示出了该船模的计算域及各边界类型。计算域全长4.5L，半宽2L，自由面以上高0.4L，自由面以下深0.8L。计算域的入口、顶面、底面及侧面均设置为速度入口类型，计算域的出口设置为压力出口类型，与船舯纵剖面重合的边界面设置为对称面类型。在计算域的入口、出口及侧面设置阻尼消波区，长度为L。计算时，释放模型的纵摇与升沉运动自由度，时间步长取为0.02 s。

图2 计算域及边界类型Fig.2 Computational domain and boundary types

计算域网格划分采用切割体网格，并在船体表面生成捕捉边界层流动的棱柱层网格。使用壁面函数法处理船体壁面网格时，以无因次距离y+定义船体表面第1 层网格厚度，通常，可以采用经验公式（3）来进行估算：

式中：Δy为船体表面第1 层网格厚度；Lw为船体湿长度。本文y+值的取值为100，并以此确定棱柱层网格的尺寸。如图3 所示，船体外的流场区域为以惯性系为参考系的背景网格，而船体附近区域则采用随船运动的重叠网格，以更好地求解船体表面流动及姿态变化。为捕捉兴波波型，对船身附近及其后一定范围内的自由面区域进行了网格加密。因月池区域以及型线曲率变化较大的球艏和船艉桨轴处流动较为复杂，同样也需对其网格进行局部加密。

图3 计算域网格划分Fig.3 Division of computational domain grids

1.3 CFD 计算验证

为确定数值求解时网格划分的合理性，采用3 套不同尺寸的网格方案进行了验证，如图4 所示。网格验证对象为不带月池的船模（Ship A），计算航速为2.196 m/s。表2 所示为采用各网格方案获得的计算结果对比。由表可知，中等数量网格方案得到的总阻力系数与试验值较为接近［10］。

图4 不同网格方案Fig.4 Different grid schemes

表2 不同网格方案的阻力计算结果对比Table 2 Calculational result comparison of resistance between different grid schemes

根据以上选取的网格方案，对流场特性予以进一步验证。图5 显示了船体表面y+分布情况。由图可见，大部分区域的y+值在100 附近，与网格划分时的设定基本相符。图6 和图7 所示为船舶航行兴波波型及船身波面抬高的计算结果，由图可见，均与试验结果［11］吻合。

以上计算验证了本套CFD 数值计算方案具有一定的可靠性。在对带月池模型（Ship B）进行计算时，其网格划分参考了上述网格方案，并对月池区域进行了网格加密，划分的网格总数约为315 万。

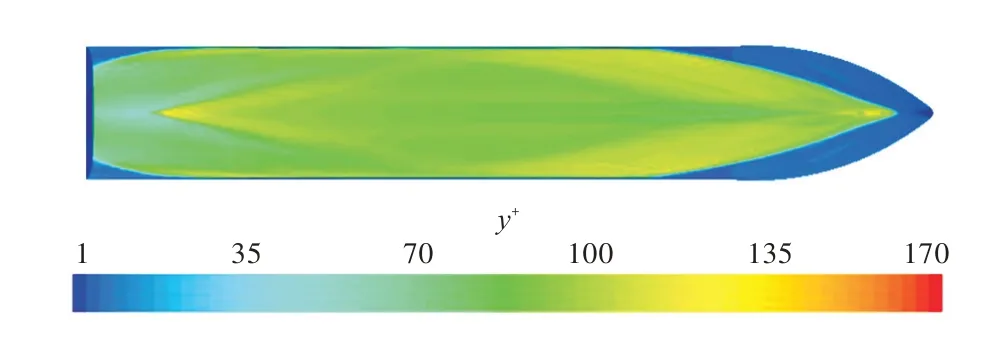
图5 船体表面y+值Fig.5 y+values of hull surface

图6 自由面波型Fig.6 Free surface wave pattern

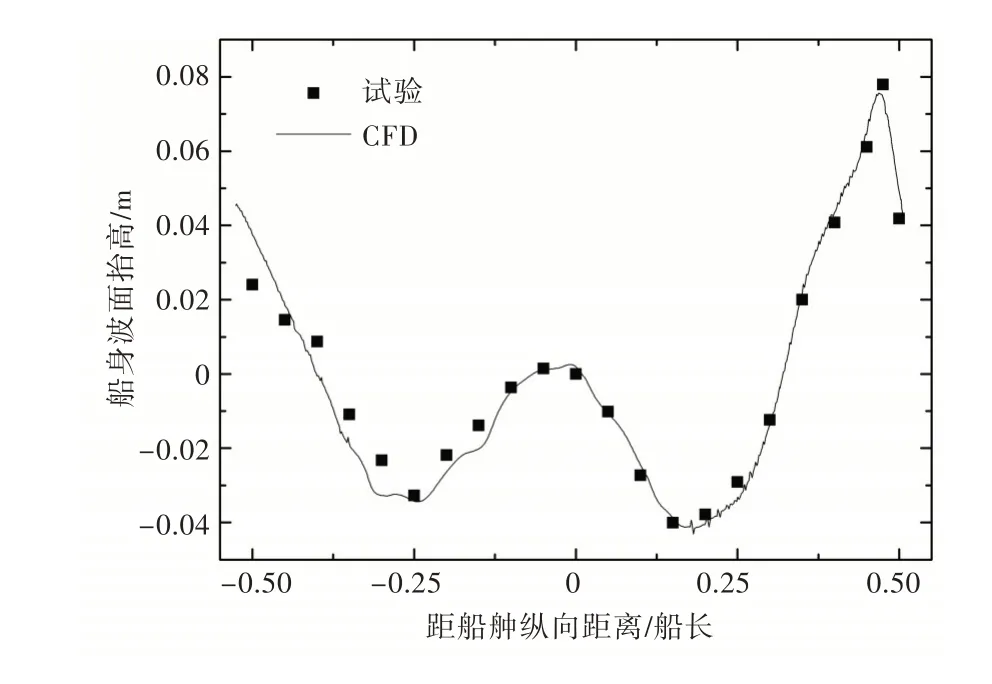
图7 船体表面波高Fig.7 Wave elevation along hull surface

2 静水阻力与流场特性研究

2.1 静水阻力分析

由于钻井船等工程船舶的航速多集中在6～16 kn，本文选取的计算航速如表3 所示。

从阻力成分上看，如图8（b）所示，摩擦阻力不仅未因月池的设置而受到显著影响，甚至还有小幅度的降低。而压差阻力则发生了爆发式的增长，在Fr=0.17 时，压差阻力值达无月池时的5 倍之多；同时，该航速下的压差阻力占总阻力的比重也由无月池时的10%上升到了42%。通过监测月池池壁的受力情况，并与压差阻力增加值进行对比，由图8（a）所示的结果可以观察到二者的值较为接近。月池内流体复杂的流动会耗散船舶自身能量，引起月池前后壁的压力差，从而在池壁上产生较大的作用力，这是船舶阻力大幅度增加的主要原因。此外，月池随边处产生并排出的漩涡向船艉输运，进入尾流，也会引起压差阻力的增加［1］。

表3 实船及模型计算航速Table 3 Computational speeds of full-scale and model ships

图8 月池引起的阻力变化Fig.8 Resistance changes caused by moonpool

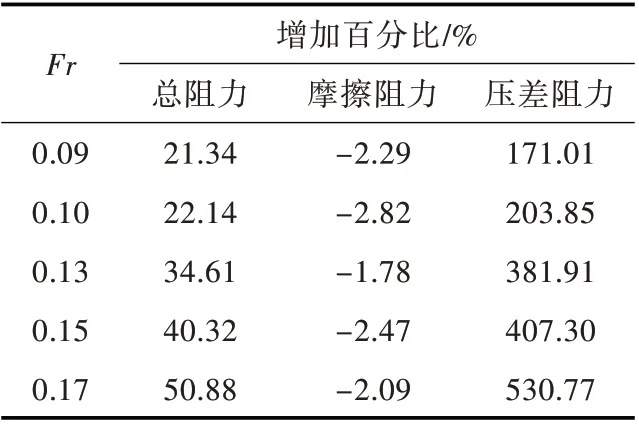
表4 各阻力成分增加百分比Table 4 Increase percentages of different resistance components

2.2 月池流场特性分析

船舶航行时，月池内流体的流动较为复杂，现对其流场特性作进一步的分析。

以Fr=0.13 为例，图9 所示为月池流场中纵剖面的速度矢量分布情况。如图9（a）和图9（b）所示，在月池后方有一大尺度漩涡占据了近一半的月池空间。在月池导边处，船底水流涌入，并因流动分离而形成顺时针旋转的漩涡，在获取足够的能量后又从导边处脱落向后输运。大尺度漩涡能量逐渐耗散，池内部分流体从月池随边排出，漩涡尺度因此缩减。此外，在池内复杂流场中还存在另外一个向后输运的小漩涡。如图9（c）所示，随着流动交换的继续，已输运至月池中部的新漩涡的强度逐渐发展增大，原大尺度漩涡和小漩涡的体积进一步缩减。由图9（d）可以观察到，新漩涡逐渐将其余2 个漩涡流动整合吸收形成新的大尺度漩涡，并于t=38.42 s（图9（e））时刻发展至鼎盛，约占据月池流场2/3 的空间，同时，月池导边处又一新漩涡开始生成。最终，流场演化为图9（f）所示状态，与图9（a）所示流场基本一致。在t=36.60～38.70 s 时刻（图9（a）～图9（f）），形成了流场内一个完整的变化周期，可以看出，周期约为2.1 s。漩涡能量耗散时，有水流流出月池冲入船体尾流，而月池前方的船底水流也不断进入月池，在船底水流与月池内水流进行质量交换的作用下，月池内的漩涡得以有持续的能量补充。图9 中，黑色线条表示月池内自由液面，船底水流自右向左流动，下文同此。

如图10 所示，船舶航行至预定航速后，其阻力曲线并非稳定成水平直线，而是呈现以2.1 s 为周期的振荡，与流场的周期性变化保持一致。同时，月池池壁所受阻力的周期性变化也与船体总阻力同步。结合流场的速度矢量与压强分布进行分析，对于图9（c）和图11（a）（图11 中，从左至右分别为月池的后壁、侧壁及前壁，下文同此），月池后方的大尺度漩涡强度大幅衰减，前壁附近自由液面升高，此时，作用于月池前壁的压力大于后壁，使得月池受到的阻力为负，即受到与船体运动方向同向的推力，此时，对应的船体总阻力谷值点为c。当流场处于图9（e）和图11（b）所示状态时，大尺度漩涡强度发展至最大，后壁处自由液面抬升，同时漩涡带动底部水流高速拍击后壁底部，月池前、后壁压力差达到最大，总阻力达到峰值点e。

图9 月池中纵剖面流场速度矢量分布（Fr=0.13）Fig.9 Velocity vector distribution of flow field in the longitudinal section of moonpool（Fr=0.13）

图10 船体总阻力及月池池壁受力时历曲线（Fr=0.13）Fig.10 Time history curves of total resistance and moonpool wall resistance（Fr=0.13）

图12 所示为月池横剖面流场变化速度矢量分布图。从中可以观察到，月池内流体整体沿垂向发生了明显的周期性活塞运动。在运动过程中，向下运动的水流与向月池内涌入的水流发生了碰撞，从而在月池两侧壁底部形成漩涡。

图11 月池池壁压强分布（Fr=0.13）Fig.11 Pressure distribution of moonpool wall（Fr=0.13）

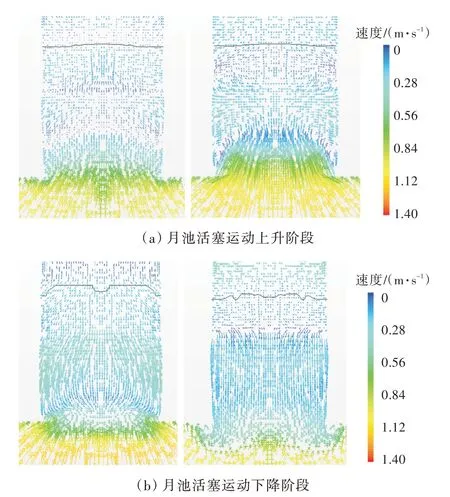
图12 月池横剖面流场速度矢量分布（Fr=0.13）Fig.12 Velocity vector distribution of flow field in the transverse section of moonpool（Fr=0.13）

数值模拟时发现，在较低航速下，月池流场内的流动除剧烈和复杂程度有所下降外，流动的周期性变化也有一定的差异。如图13 所示，Fr=0.09时的流场变化在一个周期内阻力依次出现了一大一小的峰值和谷值。与之相对应，图14 所示为流场速度矢量分布图。由图14 可观察到，图14（c）中大尺度漩涡的体积明显小于图14（a），且在这2 个时刻新漩涡强度的发展情况及池内漩涡数量也不一致。在t=32.84 s 时刻（图14（d）），大尺度漩涡强度大于t=31.12 s 时刻（图14（b）），对月池后壁产生了更强劲的作用力，使得阻力达到大峰值点d。由此可见，流场内发生了2 次不同的漩涡流动现象，从而导致阻力的大小峰、谷值迭现。

3 月池减阻改进型式研究

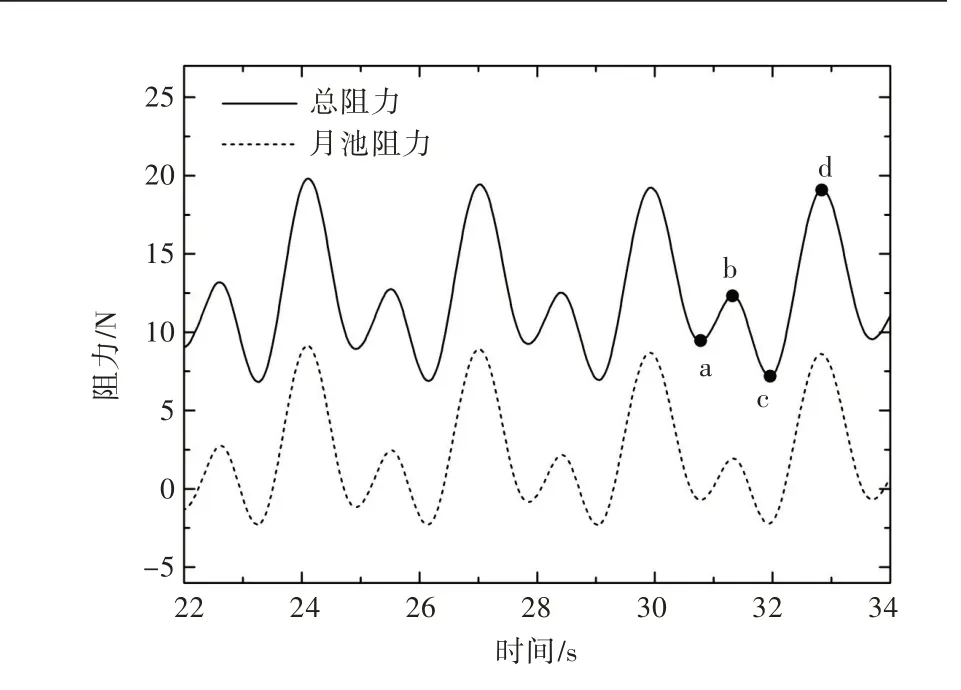
图13 船体总阻力及月池池壁受力时历曲线（Fr=0.09）Fig.13 Time history curves of total resistance and moonpool wall resistance（Fr=0.09）

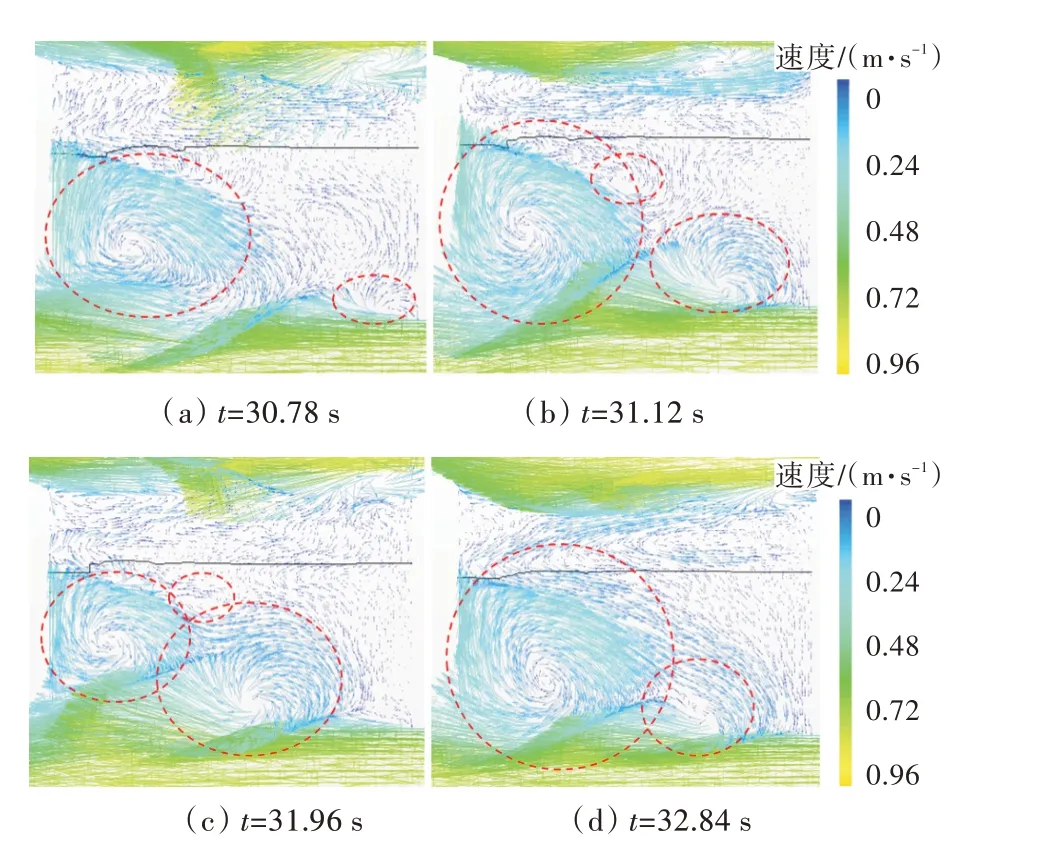
图14 月池中纵剖面流场速度矢量分布（Fr=0.09）Fig.14 Velocity vector distribution of flow field in the longitudinal section of moonpool（Fr=0.09）

基于月池内流体的流动规律，对阶梯型与切角型这2 种典型的月池减阻改进型式（对应的模型分别记为Ship C 和Ship D）进行阻力计算，并从流场细节分析其改善月池增阻的机理。

3.1 阶梯型月池

设置月池阶梯的目的原是方便工程设备在月池阶梯上的组装和移动。相较直壁式月池，阶梯型月池能够减少池内流体振荡的幅度，抑制漩涡的强度，对船舶阻力性能有着较好的改善作用，故成为一种典型的月池型式。

图15 所示为本文计算所采用的阶梯型月池。月池宽度与前文直壁式月池保持一致，于月池前、后侧增设阶梯，其中前侧阶梯长0.04 m（约为5%LM），后侧阶梯长0.28 m（约为35% LM），阶梯高度均为0.32 m。

图15 阶梯型月池Fig.15 Recess type moonpool

图16 阶梯型月池与直壁式月池阻力对比Fig.16 Resistance comparison of recess type moonpool and straight-wall moonpool

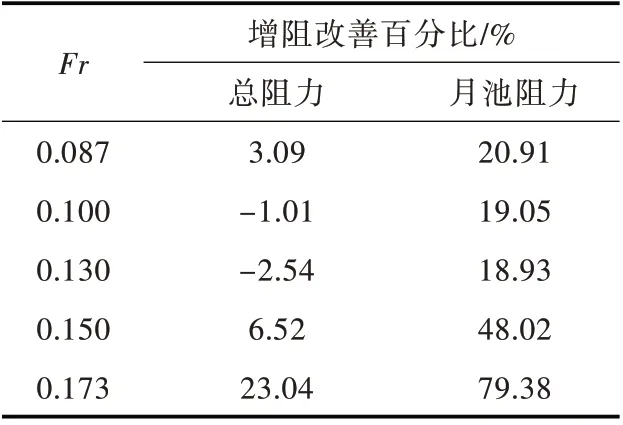
表5 增阻改善百分比（阶梯型月池）Table 5 Added resistance improvement percentages（recess type moonpool）

从流场细节来看，以Fr=0.13 的情况为例，如图17（a）所示，月池内的流体发生了纵向的晃荡运动，在撞击月池前、后阶梯后，部分流体爬上阶梯平台，再次拍击月池前、后壁。阶梯的设置等效于增加了池内自由液面在阶梯附近振荡时受到的阻尼，可消耗流体运动能量，从而抑制振荡幅度。因阶梯的设置，可以观察到池内漩涡的尺度明显减小。在图17（b）中，略去了流速小于0.05 m/s 的速度矢量。

图17 阶梯型月池中纵剖面流场速度矢量分布Fig.17 Velocity vector distribution of flow field in the longitudinal section of recess type moonpool

不同的是，图17（b）显示的傅汝德数Fr 在增加至0.17 后并未加剧月池内流体的振荡，池内的主要流动集中在月池后阶梯壁面下侧，而其他流场区域及自由液面的流动则较为平静。由图18也可以发现，此时船舶航行的阻力、纵倾与升沉值波动很小，流场处于类似于定常流动状态。对于阶梯型月池等这类变开口面积类型的月池，可以

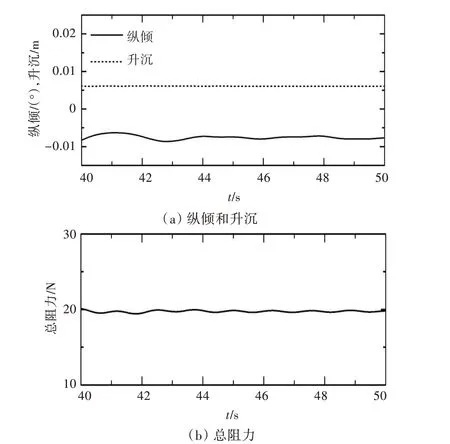
图18 航行姿态及阻力时历（Fr=0.17）Fig.18 Time histories of navigation attitude and resistance（Fr=0.17）

根据下式来估算其活塞运动的固有周期Tn［12］：

式中：A（d）为月池吃水高度d 处的开口面积；A（0）为月池底部开口面积；A（z）为月池高度z处的开口面积；κ为与月池形状有关的系数。

由表6 所示的振荡周期结果可知，随着航速的增加，阶梯型月池内流体振荡的周期逐渐偏离其活塞振荡固有周期，但尚未接近晃荡运动固有周期。随着月池内流体运动剧烈程度下降，由月池引起的增阻也大幅降低。

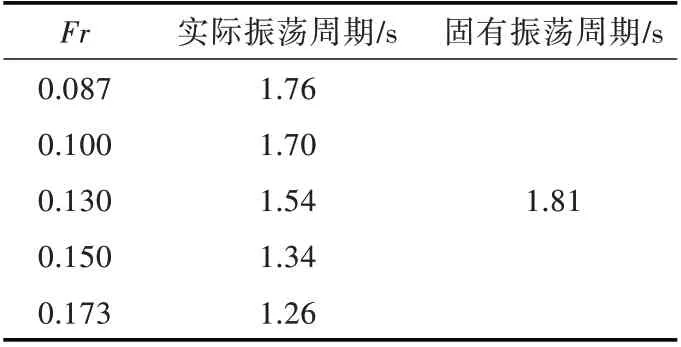
表6 阶梯型月池活塞振荡周期Table 6 Oscillation period of piston mode in recess type moonpool

3.2 切角型月池

在月池随边处进行切角处理也是典型的月池减阻方式之一，其以后倾的切角代替原月池后壁。图19 所示为切角型月池形状，切角度数取

25.5°。

图19 切角型月池Fig.19 Corner-cutting type moonpool

由图20 与表7 的计算结果可知，阻力得到了较为明显的降低，其中在Fr=0.13，0.15 航速下效果达到最佳，最大增阻改善百分比可达12.55%，月池阻力最大降幅达40%以上，为全船总阻力的降低起到了决定性的作用。

结合流场细节，如图21 所示，切角型月池内大尺度漩涡的体积较直壁式月池减小了1/3 以上，这是因为切角引导漩涡中的部分流体外排汇入船底水流中，削弱了漩涡运动的能量，即使有新的漩涡源源不断地向后补充也无法进一步增加其体积，从而使得月池内的复杂流动得到了一定程度的缓和。从压强的角度来看，如图22（b）所示，由于池内漩涡带动水流引起拍击作用，直壁式月池后壁底部附近区域的压强往往很大，而在图22（a）中可以看出，漩涡水流拍击在切角型月池后倾的切角壁面上，减小了纵向作用分力，月池前、后底部压强分布较均匀，前、后压强差减小，导致切角型月池所受阻力下降。

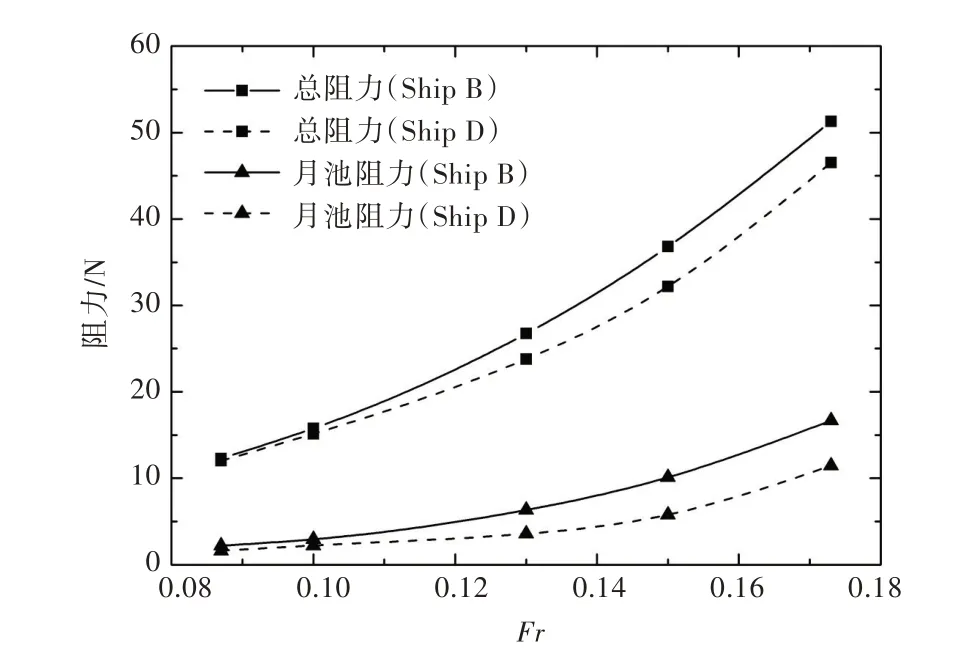
图20 切角型月池与直壁式月池阻力对比Fig.20 Resistance comparison of corner-cutting type moonpool and straight-wall moonpool

表7 增阻改善百分比（切角型月池）Table 7 Added resistance improvement percentages（corner-cutting type moonpool）

图21 切角型月池与直壁式月池大尺度漩涡规模对比（Fr=0.13）Fig.21 Large-scale vortex comparison between corner-cutting type moonpool and straight-wall moonpool（Fr=0.13）

图22 切角型月池与直壁式月池池壁压强分布对比（Fr=0.13）Fig.22 Pressure distribution comparison of corner-cutting type moonpool and straight-wall moonpool（Fr=0.13）

4 结 论

本文基于CFD 方法，对带月池的船舶进行了静水阻力与月池流场数值模拟，并结合流场的速度和压力分布特性，分析了月池对船体阻力的影响及机理，同时以阶梯型月池和切角型月池为例验证了两种改进型式月池的减阻效果。主要结论如下：

1）带月池船舶在航行过程中伴随着月池内流体复杂的流动，会耗散船体本身的能量，表现为船舶阻力的大幅增加。发生大幅增长的阻力成分为压差阻力，主要由月池前、后池壁的压力差所引起，与流场内发生的周期性漩涡运动有关。同时，船舶的阻力与航行姿态也发生了同周期的变化。

2）阶梯型月池增加了月池自由面附近流体运动的阻尼，切角型月池改善了漩涡在后池壁处的流动与影响，缓解了池内流体运动的剧烈程度，对由月池引起的阻力增加问题有较好的改善作用。

3）月池内流体运动的剧烈程度取决于实际振荡周期与固有周期的关系，前者与航速密切相关，后者则由月池尺寸参数决定，在工程应用中，应紧密结合船舶航速确定月池的型式。

本文以半模模型进行数值模拟，不考虑月池内的横向晃荡，主要是通过分析月池中纵剖面上的典型漩涡流动形式与规律来得到阻力变化与流场变化间的关系，故忽略月池内由漩涡流动的左右非对称引起的变化差异，以节省计算资源。后续，可考虑采用整模开展计算研究，以更加完整、真实地考虑月池内的流动细节。此外，在本文研究的基础上，还可进一步探究月池长宽比、吃水、阶梯长度与高度、切角度数等相关尺寸参数对船舶阻力性能的影响，以及带月池船舶在波浪中的阻力性能与流场变化，从而为月池的优化设计提供参考。