特殊类型高阶矩阵微分方程通解

吴文峰， 吴幼明

(1． 代顿大学 数学系， 俄亥俄 代顿 45469； 2． 佛山科学技术学院 数学系， 广东 佛山 528000)

*通信作者：吴幼明，男，广东广州人，佛山科学技术学院数学系副教授，博士.

0 引言

很多现实中的社会和工程技术问题的数学模型都是以微分方程的形式出现的，而工程技术问题的数学模型一般都是高阶微分方程组[1]，因此对微分方程组的求解十分重要.

目前已有很多学者对常系数微分方程组的解法研究做了不少贡献，但大部分工作都是针对一阶微分方程组的研究，如文[2-3]分别采用初等变换解法和消去法对一阶微分方程组进行了求解，文[4-6]分别采用递推公式法、矩阵解法和初等解法对一阶微分方程组的解法做了探讨，并得到了通解公式，等等. 而对高阶微分方程组的研究文献却较少，文 [7]采用降阶和欧拉方法给出了常系数微分方程组Af″-Bf=t(x)的通解公式，文[8]采用降阶法，把三阶微分方程化为3个一阶微分方程来求解且得到其实用的通解公式，文[9]得到了常系数微分方程组f‴-Bf=0的通解，文[10]采用一种特征根解法对方程Af″-Bf′-Cf=0的解做了详细的讨论，但未能给出简明通用的通解公式. 文[11]采用变量代换、特征值方法获得了常系数微分方程组Af″-aAf′-Bf=t(x)的通解公式，文献[12-13]采用降阶方法、欧拉方法和待定矩阵方法得出常系数微分方程组Af″-Bf′-Af=t(x)的通解公式.

本文在文[7,11-12]的基础上，采用待定矩阵和欧拉方法，导出了微分方程组Af″-bBf′-Bf=t(x)简明通用的通解公式，这是文[7]的延续，亦是文[11-12]的补充. 因此更具有普遍性，为高阶微分方程组的研究提供了重要的参考资料.

1 符号

为了叙述方便，引入一些记号如下：微分方程组

(1)

其中fi=fi(x)(i=1,2,3)是关于x的函数，ti(x)(i=1,2,3)是关于x的二次多项式，aij,bij,b(i,j=1,2,3)为常数，将方程组(1)写成矩阵形式：

(2)

(3)

则式(2)可写为

(4)

2 方程的通解

2.1 齐次方程的通解

先采用特征根法解方程(4)对应的齐次方程，其形式如下：

(5)

(6)

矩阵D的特征多项式为

(7)

(8)

1)当λ=λ1时，解特征方程(D-λ1E6)ξ=0，求出特征根λ1对应的特征向量ξ1，即

(9)

对式(9)系数矩阵作初等变换，得ξ14=λ1ξ11,ξ15=λ1ξ12,ξ16=λ1ξ13. 而ξ11,ξ12,ξ13由下面方程组解出:

(10)

解方程(10)，得对应λ=λ1时的特征向量为ξ1=[ξ11,ξ12,ξ13,λ1ξ11,λ1ξ12,λ1ξ13]T.

同理可求出特征根λ2,λ3,λ4,λ5,λ6对应的特征向量ξ2,ξ3,ξ4,ξ5,ξ6，其形式如下：

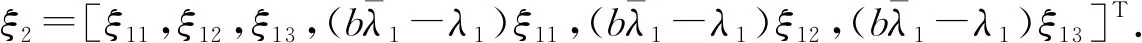
3)当λ=λ3时，得特征向量为ξ3=[ξ31,ξ32,ξ33,λ3ξ31,λ3ξ32,λ3ξ33]T.

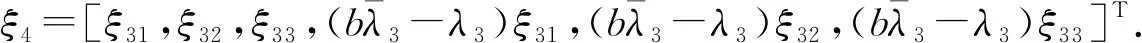
5)当λ=λ5时，得特征向量为ξ5=[ξ51,ξ52,ξ53,λ5ξ51,λ5ξ52,λ5ξ53]T.

(11)

取式(11)的前三项及前面得到的特征值和特征向量的结论，可得方程(5)的通解为

V[exp(Λ1x)C1′+exp((bΛ2-Λ1)x)C2′].

(12)

2.2 非齐次方程的特解

ft(x)=-B-1t(x)+bB-1t′(x)-(b2B-1+B-1AB-1)t″(x).

(13)

由式(12)与式(13)得方程(2)的通解f=V[exp(Λ1x)C1′+exp((bΛ2-Λ1)x)C2′]+ft.

注当b=0时，方程(2)的通解公式为

[f1,f2,f3]T=V[exp(Λ1x)C1′+exp(-Λ1x)C2′]-B-1t(x)-B-1AB-1t″(x).

(14)

式(14)与式(12)、式(13)[7]一致，说明本文的通解公式是文[7]的拓展.

3 算例

用本文方法求下列方程组的通解

(15)

解将式(15)写成矩阵的形式如下：

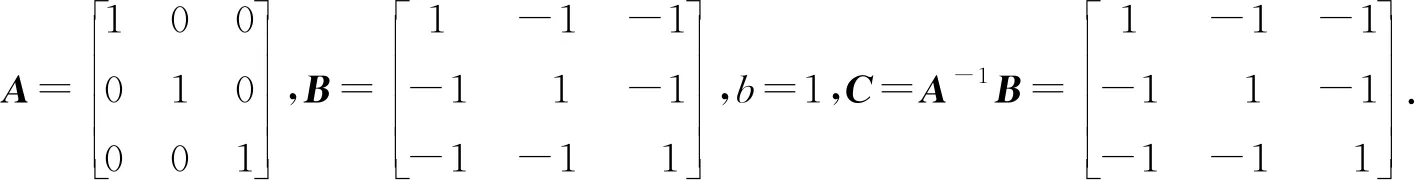
则方程组(15)的通解为

即

(16)

式(16)经验算，确是式(15)的解.

4 结语

本文方法所得通解具有一般性，对分析任意初始条件的问题带来了方便. 微分方程组的右端非齐次项取不同形式时可得到不同形式的特解. 通解公式可通过编程进行电算. 本文只讨论了二阶微分方程组通解和特解公式的情况，而目前对三阶及以上的微分方程组的研究还很少，研究的理论和方法也不够完善，微分方程组的通解和特解之间的联系与区别也还有待发掘. 后续工作可着力于三阶微分方程组的通解和特解的理论解公式的推导，以及推导这些公式所采用的方式方法研究.