基于多因素的焊接结构疲劳裂纹扩展速率分析
2020-06-28白林越
白林越,邵 飞,高 磊,徐 倩
(中国人民解放军陆军工程大学 野战工程学院,南京 210007)
1 引 言
疲劳是材料在循环荷载作用下的损伤累积过程,极易导致结构的脆性断裂,降低结构的安全性和使用寿命。金属结构的疲劳失效分为疲劳裂纹的萌生、稳定扩展和失稳扩展三个阶段,其中,稳定扩展阶段作为金属结构疲劳寿命的主要控制阶段,成为各国学者关注的重点。Zhu等[1]根据试验检测数据,建立了残余应力分布在疲劳裂纹扩展过程中的演化模型,得到了残余应力对疲劳裂纹扩展速率的影响规律。贾心怡等[2]利用Walker公式和能量释放准则,提出了全尺寸管道疲劳裂纹扩展公式,分析了动、静态扩展时裂纹四周的应力变化特点。Paolino等[3]基于Paris公式,建立了适用于超高周疲劳裂纹的扩展速率计算模型,预测了不同初始缺陷条件下AISI H13钢的极限寿命。
随着焊接在制造加工过程中的广泛应用,焊接结构已经成为金属结构的重要组成部分。但是,焊接结构的疲劳性能却与金属基材存在较大差异。Tsay等[4]指出,由于显微组织结构和结构内应力的不同,焊接结构近焊缝处的疲劳裂纹扩展速率显著高于金属基材。Lemos等[5]通过模型试验的手段也得出了相同结论,同时指出焊缝区是疲劳裂纹萌生的高发区域。因此,探究焊接结构疲劳裂纹扩展速率的控制因素有助于提高焊接结构的安全性和使用寿命。但是,焊接结构疲劳性能的模型试验需要消耗大量的经济和时间成本,不利于焊接结构疲劳裂纹扩展行为的深入研究,而现有的疲劳理论大多基于单一金属结构建立,难以用于焊接结构疲劳裂纹扩展速率的分析。因此,建立适用于焊接结构的疲劳裂纹扩展速率计算模型对研究焊接结构疲劳裂纹扩展速率的控制因素具有十分重要的 意义。
本文基于Donahue等[7]提出的疲劳裂纹扩展速率计算模型,通过引入形状系数、张开比和残余应力等参数,建立了适用于焊接结构的疲劳裂纹扩展速率计算模型,并通过试验数据验证了理论模型的有效性,为研究焊接结构疲劳裂纹扩展速率的控制因素提供了一种切实可行的理论方法。同时,通过建立的计算模型研究了多种因素对焊接结构疲劳裂纹扩展速率的影响规律,提出了一些设计建议。
2 焊接结构疲劳裂纹扩展速率计算模型
2.1 基础模型选用
Paris等[6]在断裂力学的基础上,提出了用于计算疲劳裂纹扩展速率的Paris公式,随后文献[7-9]提出了多种适用范围更广的疲劳裂纹扩展速率计算模型。但是,随着计算模型适用范围的增大,需要通过试验测定的参数也越来越多,影响了计算模型的实际应用。因此,为了在减少未知参数的同时尽可能多地考虑焊接结构疲劳失效的不同阶段,本文以Donahue等[9]提出的疲劳裂纹扩展速率计算模型为基础,建立的计算模型基本形式为
(da/dN)m=C·[ΔK-ΔKt h]m
(1)
式中(da/dN)m为疲劳裂纹扩展速率,ΔK和ΔKt h分别为应力强度因子幅和应力强度因子幅门槛值,C和m为通过疲劳试验测得的材料常数。基于该模型建立的焊接结构疲劳裂纹扩展速率计算模型可以用于分析疲劳裂纹的萌生和稳定扩展阶段,符合本文的研究目的。
2.2 应力强度因子幅
焊接结构在加工过程中会受到高水平不均匀热输入的影响,使焊接区域表面产生不规则形变。因此,在计算焊接结构表面裂纹的应力强度因子时需要对传统的应力强度因子计算式进行改进。
焊接结构表面裂纹的应力强度因子幅可表示为[10]
(2)
式中Φ0为第二类完全椭圆积分,Ms为自由表面修正系数,MT为有限厚度修正系数,Mk为焊趾修正因子,Δσ为循环应力幅,a为裂纹深度。
当焊缝表面无纵向角焊缝时,可采用联合修正系数MsMT/Φ0对焊接结构表面裂纹的应力强度因子进行修正[11],
(3)
式中B为焊接板件厚度。
焊趾修正因子Mk的取值为[12]
(4)
q=ln(11.584-0.0588θ)/2.3
(5)
式中θ为与焊缝余高有关的参数,如图1所示,150°≤θ≤180°。
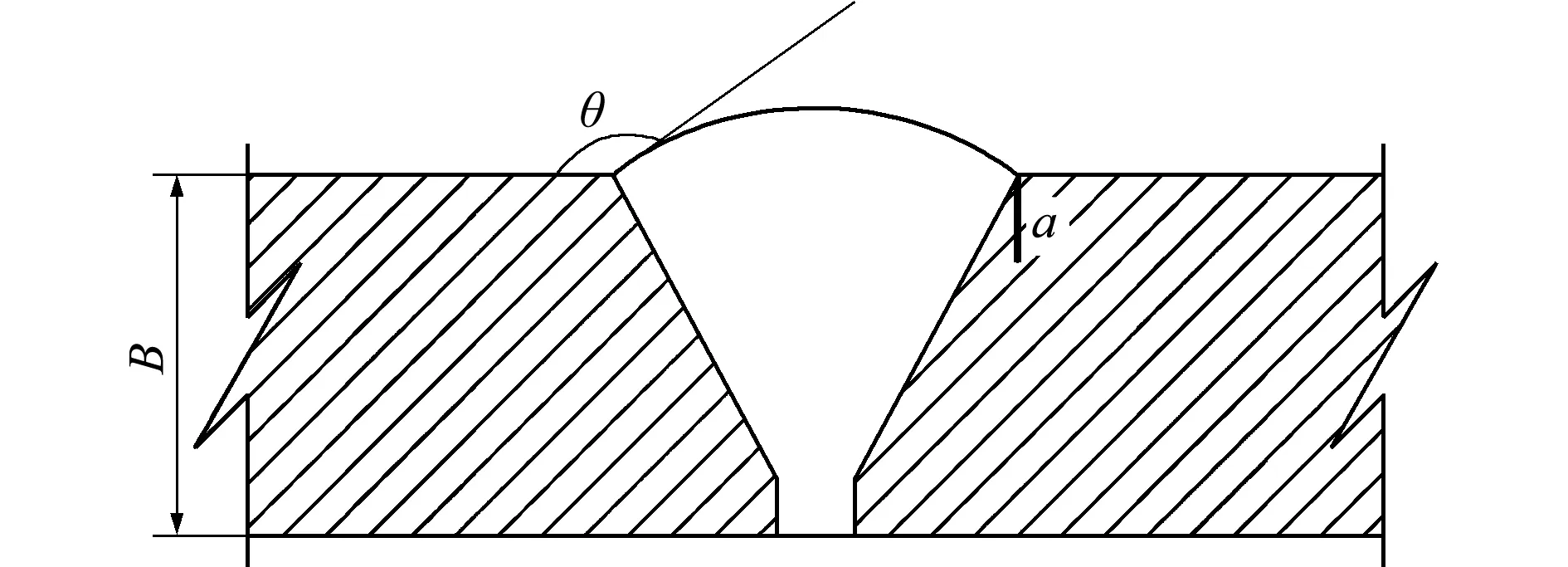
图1 参数θ的物理意义
Fig.1 Physical significance ofθ
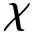
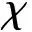
(6)
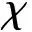
(7)
由于 Δσ=σmax(1-R)
(8)
则将式(8)代入式(7)得
(9)
式中σmax为每一循环中的最大应力,R为应力比。
将式(3~6)代入式(9)即可对焊趾表面裂纹的应力强度因子幅进行求解。
2.3 应力强度因子幅门槛值(ΔKt h)
ΔKt h与金属种类、服役环境和荷载应力比密切相关,在计算时涉及的ΔKt h一般通过试验测得,这无疑增加了试验任务。为解决这一问题,Yu[11]提出了疲劳裂纹扩展门槛值的概念,并通过对大量试验数据的总结,得出了疲劳裂纹扩展门槛值的经验公式,
(10)
式中at h为疲劳裂纹扩展门槛值,b1为疲劳强度系数,
b1=-1/m
(11)
当a≥at h时,疲劳裂纹进入稳定扩展阶段。则焊接结构表面裂纹的应力强度因子幅门槛值为
(12)
2.4 张开比
仅当循环拉伸荷载超过一定临界值时,焊接结构中的疲劳裂纹才会全部张开,这一现象称为闭合效应,计算时可以通过向计算模型中引入裂纹张开比的方式考虑疲劳裂纹的闭合效应。此时,有效应力幅Δσeff与实际应力幅Δσ的关系为
Δσeff=UΔσ
(13)
式中U为裂纹张开比。
由于张开比的试验测定方法复杂,研究人员始终在探寻张开比的理论计算方法,但取得的成果大多局限于单一材料,而不具备普遍适用性[14-16]。直到Newman[17]提出了一种能够考虑多种因素、适用范围广泛的张开比计算公式,
U=(1-f′)/(1-R)
(14)
式中
(15)
(16)
A1=(0.415-0.071α)σmax/σf
(17)
A2=1-A0-A1-A3
(18)
A3=2A0+A1-1
(19)
式中α为应力/应变约束系数(平面应力状态下α=1,平面应变状态下α=3),σf为流变应力,
σf=1.15(σy+σu)/2
(20)
式中σy为屈服强度,σu为抗拉强度。将式(15~20)代入式(14)即可对张开比进行求解。
2.5 残余应力
ASME和API579中规定,在计算含残余应力场的裂纹尖端应力强度因子时,可直接将有裂纹无残余应力和无裂纹有残余应力两种情况下的应力强度因子进行叠加,求得总的应力强度因子值。因此,当残余应力存在时,裂纹尖端的有效应力强度因子为
(21)
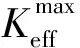
(22)
残余应力引起的应力强度因子可采用权函数法计算。若垂直于裂纹扩展方向的残余应力分布函数为σres(x),则残余应力引起的应力强度因子增量可表示为
(23)
式中x为沿裂纹扩展方向距裂纹萌生点的距离,h(x,a)为权函数。
为便于积分,可将残余应力与裂纹之间的位置关系简化为分段函数,如图2所示[11]。
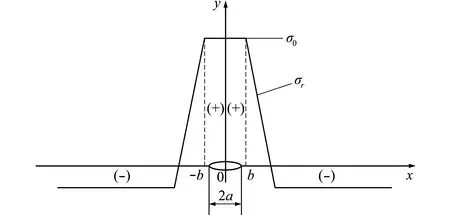
图2 残余应力分布简化形式
Fig.2 Simplified form of residual stress distribution
若a≤b,则有
(24)
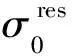
若b (25) 将式(21,23~25)代入式(22)即可得到考虑残余应力后循环荷载的有效应力比,进而将残余应力的影响引入到计算模型中。 在确定了焊接结构的形状系数、应力强度因子幅、应力强度因子幅门槛值、张开比和残余应力后,将式(1)解析过程中涉及的应力幅Δσ和应力比R替换为有效应力幅Δσeff和有效应力比Reff,并将式(9,12,13)代入式(1)即可得到适用于焊接结构的疲劳裂纹扩展速率计算模型, (26) 焊接结构疲劳裂纹扩展速率计算模型的解析流程如图3所示。 为验证计算模型的有效性,本文收集了X100、A106 Gr B和2195-T8焊接结构的疲劳裂纹扩展速率试验数据[18-20],并将计算结果与试验结果进行了对比,如图4所示。 可以看出,本文提出的计算模型能够准确预测A106 Gr B和2195-T8焊接结构的疲劳裂纹扩展速率。但是,对X100钢焊接结构疲劳裂纹扩展速率的预测结果与试验结果存在一定偏差,最大偏差值为62%。这是由于文献[18]试验中的腐蚀环境加速了X100钢焊接结构疲劳裂纹的扩展,使其扩展速率显著高于惰性环境下焊接结构疲劳裂纹的扩展速率[21,22]。因此,本文提出的焊接结构疲劳裂纹扩展速率计算模型能够有效预测焊接结构在惰性环境下的疲劳裂纹扩展速率,而对腐蚀环境下焊接结构腐蚀疲劳裂纹扩展速率的预测结果低于实际值。 图3 计算模型解析流程 Fig.3 Analytical process of calculation model 通过计算模型可以看出,焊板厚度和焊缝余高的改变均会影响焊接结构的形状系数,进而影响焊接结构疲劳裂纹的扩展速率。焊板厚度和焊缝余高对焊接结构疲劳裂纹扩展速率的影响如图5所示。 可以看出,焊板厚度的增大会降低焊板截面的有效面积,降低循环荷载作用下单位截面承受的应力幅,进而降低焊接结构的疲劳裂纹扩展速率。同时,随着裂纹扩展深度的增加,焊板截面的有效面积逐渐降低,提高了疲劳裂纹的扩展速率(图5(a))。而疲劳裂纹扩展到不同深度时,θ对疲劳裂纹扩展速率的影响规律不同。当裂纹深度较小时,疲劳裂纹扩展速率随θ的增大呈先升高后降低的趋势;当裂纹扩展到一定深度后,疲劳裂纹扩展速率不再随θ的增大而降低,而是始终保持增大趋势(图5(b))。因此,在对焊接结构表面形状进行设计时应保有一定的焊缝余高。 有效应力比是影响疲劳裂纹扩展行为的重要因素,能够直接影响裂纹的扩展速率。有效应力比对焊接结构疲劳裂纹扩展速率的影响如图6所示。 可以看出,焊接结构疲劳裂纹的扩展速率随着有效应力比的增大而降低。这是由于有效应力比较大时,疲劳裂纹扩展过程中产生的滑移带宽度降低,进而降低了疲劳裂纹的扩展速率。同时,在疲劳裂纹扩展的不同阶段,有效应力比对焊接结构疲劳裂纹扩展速率的影响规律基本相同,说明裂纹深度的变化不会明显改变有效应力比对焊接结构疲劳裂纹扩展速率的影响。 图4 计算模型有效性验证 Fig.4 Validation of calculation model 由式(21,22)可知,残余应力能够通过改变循环荷载有效应力比的方式对焊接结构疲劳裂纹的扩展速率产生影响。残余应力对焊接结构疲劳裂纹扩展速率的影响如图7所示。 图5 焊板厚度和焊缝余高对焊接结构疲劳裂纹扩展速率的影响 Fig.5 Influences of plate thickness and excess weld metal on fatigue crack growth rate of welded structures 图6 有效应力比对焊接结构疲劳裂纹扩展速率的影响 Fig.6 Influence of effective stress ratio on fatigue crack growth rate of welded structures 可以看出,残余应力的存在会提高疲劳裂纹的扩展速率,且残余应力对疲劳裂纹扩展速率的促进作用随着疲劳裂纹深度的增加而增大。因此,在疲劳裂纹扩展到一定深度后,残余应力对焊接结构疲劳裂纹扩展速率的促进作用会大幅增加,降低焊接结构的疲劳寿命。在对焊接结构的抗疲劳性能进行设计时必须考虑残余应力对结构性能的影响,以保证焊接结构的使用寿命和安全性。 图7 残余应力对焊接结构疲劳裂纹扩展速率的影响 Fig.7 Influence of residual stress on fatigue crack growth rate of welded structures 本文通过向Donahue等[7]提出的疲劳裂纹扩展速率计算公式中引入形状系数、张开比和残余应力等参数,建立了适用于焊接结构的疲劳裂纹扩展速率计算模型,并利用该模型分析了多种因素对焊接结构疲劳裂纹扩展速率的影响规律,得出结论如下。 (1)焊板厚度的增加会降低疲劳裂纹的扩展速率,而焊缝余高对疲劳裂纹扩展速率的影响规律随着a/B的改变而改变,需要根据实际结构进行分析,但在对焊接结构表面形状进行设计时应保有一定的焊缝余高。 (2)随着有效应力比的增大,焊接结构疲劳裂纹的扩展速率逐渐降低,且有效应力比对焊接结构疲劳裂纹扩展速率的影响规律在疲劳裂纹扩展的不同阶段基本相同,说明有效应力比对焊接结构疲劳裂纹扩展速率的影响不会随着裂纹深度的变化而变化。 (3)残余应力的增大会提高疲劳裂纹的扩展速率,且裂纹深度越大,残余应力对疲劳裂纹扩展速率的促进作用越显著,因此在对焊接结构的疲劳性能进行设计时,须考虑残余应力对结构安全性和使用寿命的影响。3 模型验证
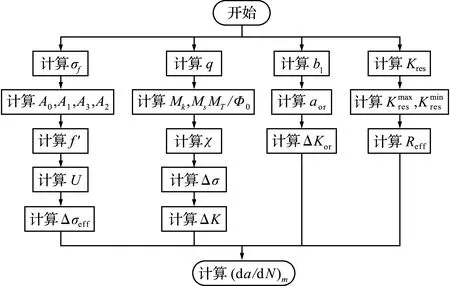
4 影响因素分析
4.1 形状系数
4.2 有效应力比
4.3 残余应力

5 结 论
