侗族建筑数学元素调查研究

吴秀吉，张和平

（1.凯里学院附属中学，贵州凯里 556000；2.凯里学院，贵州凯里 556011）

侗族是中国南方众多少数民族中人口较多的农耕民族，主要分布在黔、湘、桂三省毗邻区及鄂西南地区.不同的地域环境导致侗族人民生活习惯、人文甚至人的性格、思想观念等都会带有地理环境的烙印，同时也产生了与地理环境相应的建筑技艺［1］.侗族居住在气候温和、多雨湿润的山区，加上侗族人民长期积淀的传统文化习俗、生活智慧和农耕生产创造，造就了独具特色的侗族民居、鼓楼等建筑文化体系，调查发现，侗族建筑的装饰、结构及建造技艺蕴涵着丰富的数学元素资源.

图1 民居建筑

1 侗族建筑中的几何变换

1.1 平移变换

简化后的鱼儿菱形和波形纹在侗族传统民居建筑中较为常见，由于侗族传统民居建筑所具有的实用功能占主导位置的特性，一些装饰性的图形图像就常与民居建筑上的结构性、功用性构件结合在一起［2］.（图1）中的民居建筑是将鱼儿简化成菱形、波纹形与窗饰结合起来的，这些点缀看似平淡无奇，但能使建筑立面图形变得丰富起来.图1 中的窗格共三层，每一层花格都是由“V”形木条左右平移而得到的.

1.2 对称变换

侗族传统民居用椽子垂直安放在檩条上，上面盖有小青瓦，椽子起到支承瓦面的作用.而屋脊基本上都是小青瓦堆叠的清水脊，中间位置用小青瓦堆砌成轴对称图形.如图2 所示，小青瓦堆砌千姿百态造型万千，有钱币造型的，也有花朵造型的，但不管这些青瓦堆砌数量的多少，排列的方式是圆还是方，其屋顶从立面上看，整体图像都是呈纵向轴线对称的布局方式［2］.

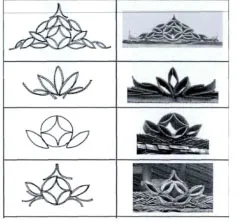
图2 小青瓦堆砌造型

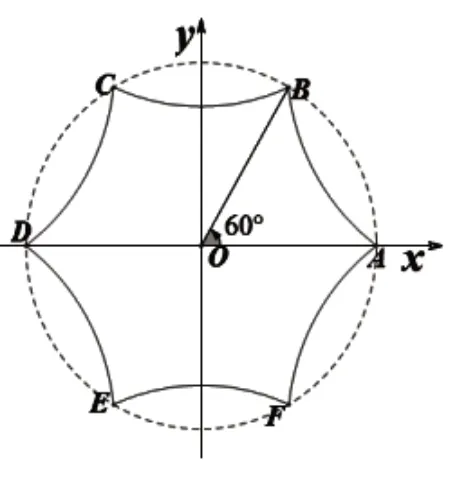
图3

1.3 旋转变换

旋转一个60o或60o的整数倍角都一定和原图形重合.即图中的正六边形ABCDEF是通过点E在变换矩阵C=的5次作用下实现的.通过基本旋转变换实现的多面体状筒形的鼓楼建筑，达到减少受力面积，形成一个中心对称图形，是鼓楼建筑平衡的优化设计［3］.

图4

2 侗族建筑中的初等几何

侗族鼓楼很大一部分都修建得很高大，非常雄伟、壮观，从建造技艺来看，可算得上是侗族木构建筑之最.如此高大的建筑物层与层之间是用木制楼梯（图4）连通的.进一步调查发现在黔东南州境内的榕江、黎平、从江有部分建筑师用比例的方法去制作连接层与层之间的相应楼梯，其过程如下：

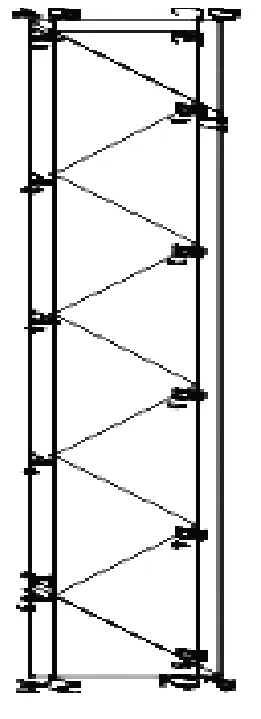
图5

图6

首先，在（图4）中测量出A′B′=a,B′C′=b;其次，在（图5）中的长方形ADPM（木枋）中取AB=CD=PQ=NM，用墨线分别连接BN、CQ,由AB:BA1=a:b便可确定A1的位置，过A1作A1E⊥CQ垂足为E，再由A1E:EB1=a:b便可确定B1的位置，过A1、B1作直线A1B1与木枋的边缘分别交于A、U，过B1作A2B1⊥A1B1交BN于A2，并连接A2B1，用同样的方法作出Ai+1Bi⊥AiBi,Bi+1Ai+1⊥Ai+1Bi垂足分别为Bi,Ai+1(i=1,2,3,…)(如图4);最后，沿AiBi、Ai+1Bi、Ai+1Bi+1(i=1,2,3,…)凿开木槽，按同样的方法把另一块木枋做好后，安装上相应木板便可得到楼梯（图6）（引自文献［2］）.

图7

图8

图9

侗族建筑师在装修过程中通常在封头板上制作五角星、铜贯钱等图案（如图7）［4］.侗族师傅在制作五角星（图8）时，首先是通过制作正五边形，然后再连接其对角线去实现的，其过程如下：

首先，作线段AL（AL的长度小于封头板的宽度），取AL的中点O，以O为圆心，OA为半径画圆，过O作BD⊥AL垂足为O，取AO1=OO1，连接O1B，并取O1O2=O1B，以B为圆心，BO2为半径画弧分别与圆O交于F,E，再分别以F,E为圆心BO2为半径画弧，分别与圆O交于G,H，依次连接B,F,G,H,E即可得到正五边开形.

其次，分别连接BG,BH,FE,FH,GE使BG⋂EF=B′,BG⋂FH=C′，BH⋂EF=A′,BH⋂EG=E′,FH⋂EG=D′。

最后，用尖尾锯沿BB′FC′GD′HE′EA′B锯开即可以得到一个五角星.

在图9 中，首先，取线段A′C′（A′C′的长度小于封头板的宽），取A′C′的中点O，过O作B′D′⊥A′C′垂足为O，使C′O=A′O以O为圆心，OA′为半径画圆.其次，分别以OA′,OB′为邻边作正方形AOB′B.用同样的方法作出正方形C′OB′C,C′OD′D,A′OD′A。再次，分别以A,B,C,D为圆心,AA′,BB′,CC′,DD′为半径画弧最后，用尖尾锯沿弧和圆O的圆周锯开，即可得到“铜贯钱”花形.

图10 卯榫

图11

图12

图10是侗族民居装修卯榫部分结构图.木匠师傅在木枋CBED的CD边上取点A（其中AC≤C′F′），连接AB.并在木枋C′D′E′F′的C′D′和C′F′上分别取A′、B′使得A′C′=BC、C′B′=AC（图11）.然后把RTΔABC做成相应的榫，把RTΔA′B′C′做成相应的卯口.最后，把木枋C′D′E′F′逆时针旋转90o平移与木枋CBED结合成（图12）.

图13 牡丹花窗

图14

侗族民居建筑中的牡丹花窗（图13）是由正方形和八边形（虽然不是正八边形，但它的各个顶点都在同一个圆周上）两种几何图形镶嵌成的一个平面，所不同的是，此正方形的边长和八边形长边的边长相等是短边边长倍［4］.这为研究当正方形的边长与八边形长边的边长相等是短边边长的倍，能镶嵌成一个平面（图14）提供了现实模型.

以上足以看出，侗族人民对初等几何的应用达到较高的水平.

3 侗族建筑中的相关计算

3.1 等差数列的应用

侗族建筑水步的计算一般是以前后（进深）纵向的尺寸为依据，这也是一种统一的规定［6］.假设一幢建筑从前檐柱到后檐柱的纵向进深为2.76丈，依照东家的要求要建五柱八瓜的木房，即前后都为6 步水，中间有12 个空位，再拿12 去均分2.76丈，每个空间的距离就是2.3 尺.在此基础上，还要考虑前后檐伸挑出去的一步水，应同样为2.3尺.其实这2.3 尺就是每相邻两根檩条的平行距离，这与每步水规定在2尺至2.5尺相吻合.

有了步水的距离尺寸，就可以很方便地计算顶层坡面的倾斜度.通常用五分水到底的“人”字形的水面，即5分水就是从脊梁到檐口都是5分水到底，以2.3 尺为例，其每一步水降1.15 尺距离.也就是说，从脊梁到第一瓜应降1.15 尺的高度，按这一尺寸一直降到檐口.即伸挑出去的挑檐枋比檐柱矮1.15 尺，以此类推，前后如此，从脊梁直至檐口.把第一步水应降的距离不妨令为a1=1.15，相邻两步水下降的距离为d=1.15，则步水的计算满足下列公式：

一般的侗族建筑从脊梁到檐口的距离是递增的，从而侗族民居建筑从脊梁到檐口的距离构成一个递增的等差数列.

综上所述，因为建筑师在建造侗族民居建筑时，因地基的大小不同，所制作的“人”形架的大小也各不相同，但建筑师根据这样的推算，便很快确定需要材料的多少，避免不必要浪费［5］.

3.2 正八边形的相关计算

修建八角形鼓楼时，涉及正八边形半径R与边长a的相关计算.今天可以用公式a=2Rsin22.5o表示.而22.5o不是特殊角，计算结果只能取其近似值.但古代侗族对角度的概念的认识并不是很清晰，进一步调查发现与黔东南州黎平县毗邻的通道县境内有部分鼓楼建筑师用以下计算公式：

正八边形边长=正八边形的半径×0.78.

以这个公式为依据，通过扩大或缩小可以算出正八边形边长的实际长度.如果我们按照现代数学中的三角函数的方法来求，则有：由于正八边形的同圆心角为45o，过圆心作边的垂线，则平分边长和圆心角，取正八边形的半径为R=1，从而边长a=2×1×sin22.5o≈0.765，由 |0.78-0.765 |=0.015，取这个值与理论值相差很小，又由于在实际测量时也存在误差，鼓楼建筑师选用这个公式是有道理的且符合实际，它显然是一个较好的近似计算公式，这是侗族鼓楼建筑师在长期的实践中总结得到的结果.

4 侗族建筑中蕴含的数学思想方法

4.1 民居建筑的笛卡儿积思想

侗族传统民居建筑前后左右的定位应以中堂太师壁神龛上的“天地君亲师位”的“师”为定点，面朝的方向不前，背靠太师壁为后，左右自然分清.若要建一幢五柱三开间的干栏式民居，应有四排柱子的组合如（图15）.以中堂为准界线，便有左右各两排柱子，又以中柱为准界线，便又有前2 柱、前檐柱、后2 柱、后檐柱之分.这样，这幢民居建筑便有：左1 排中柱、左1 排前2 柱、左1排前檐柱，左1 排后2 柱、左1 排后檐柱；左2 排中柱、左2 排前2 柱、左2 排前檐柱，左2 排后2 柱、左2 排后檐柱.右1 排中柱、右1 排前2 柱、右1 排前檐柱，右1 排后2 柱、右1 排后檐柱；右2 排 中柱、右2 排前2 柱、右2 排前檐柱，右2 排后2 柱、右2 排后檐柱［6］.这样标记的目的，是为了方便人们在立房子时能够准确地找到相应的柱子和木枋，防止出错.

图15

根据图15，把每根柱子所在位置标记如下：

C1:左1 排中柱，B1:左1 排前2 柱，A1:左1 排前檐柱，D1:左1排后2柱，E1:左1排后檐柱；

C2:左2 排中柱，B2:左2 排前2 柱，A2:左2 排前檐柱，D2:左2排后2柱，E2:左2排后檐柱.

C4:右1 排中柱，B4:右1 排前2 柱，A4:右1 排前檐柱，D4:右1排后2柱，E4:右1排后檐柱；

C3:右2 排中柱，B3:右2 排前2 柱，A3:右2 排前檐柱，D3:右2排后2柱，E3:右2排后檐柱.

如果我们用两个集合中的元素来表示上面的排和列，设X={a1,b1,c1,d1} ；Y={a2,b2,c2,d2,e2} ；其中a1,b1,c1,d1分别表示“左1”，“左2”，“右2”，“右1”，a2,b2,c2,d2,e2分别表示“前檐柱”，“前2柱”，“中柱”，“后2柱”，“后檐柱”，民居建筑结构构件方位则为：

图16

在平面直角坐标系上描述这些点，即可以得到图16.这说明侗族传统建筑结构中蕴含有笛卡儿积思想.同时也说明侗族人民对平面笛卡儿积思想有了较好的理解，并在现实生活中得到较好地运用.

4.2 鼓楼中的墨线分割思想

修建六角鼓楼时，需要制作正六边形.在修建过程中，侗族建筑师通常将圆进行分割，使其平均分成六等分.然后利用平移的方法分别在柱头上进行分割（分割时以中墨为基准），并通过分割下来的点作出墨线，然后利用鼓楼对称的性质和空间中点的对应关系作出其他墨线，这些墨线与墨点在鼓楼上存在一一对应关系［4］.例如将一个圆木六等分时，其具体制作方法如下：

图17

图18

首先，在准备好的呈圆柱（实际上是不规则）的原木，两头（横截面（如图17））吊垂线A D(或A′D′)，分 别 连 接A A′、DD′.取A D(或A′D′)的 中 点O(或O′)，在OA(或O′A′)上 取 点（其 中O A1＜O A(或＜O′A′)），以O(或O′)为 圆 心，O A1(或)为半径作⊙O(或⊙O′)，与O D(或O′D′)交于其次，分别以为圆心，以、为半径画弧与⊙O(或⊙O′)分别交于、，连 接、C1F1(或)延长线与横截面的边缘分别交于B(或B′)、E(或E′)、C(或C′)、F(或F′).最后，用墨线分别连接AA′、B B′、CC′、DD′、EE′、F F′,然后在两条相邻的墨线分别任取一点沿着垂直于O O′打孔（或凿柱眼），这两个孔（或柱眼）所确定的方向角成60o，从而实现了六等分圆（图18）.

综上所述，侗族鼓楼及民居的建造涉及比例、等差数列、平面镶嵌、平移、对称及位似变换等数学知识.她展现侗族建筑艺术千百年来所形成的数学思维习惯和特征以及对经典数学有了较好的理解和应用，同时充分展示了侗族人民的数学智慧.