大断面顺槽掘进空顶距的确定

2020-06-28李子长

煤矿现代化 2020年4期

李子长

（山西宏厦第一建设有限责任公司，山西阳泉 045008）

在煤层掘进施工过程中，由于要为施工预留一定的工作区域，因此空顶区域在施工过程中是必不可少的。然而由于空顶区域短时间内不可避免地处于自由悬空状态、缺少足够的支撑，因此空顶区域可能存在失稳、破坏的情况。即使空顶区域未发生破坏，考虑到空顶区域极易出现的裂纹及其扩展，这些小裂纹及其扩展很可能会在极大程度上削弱岩层的稳定性。此外，这些小裂纹在耦合作用下的扩展范围往往是很大的，并有向岩层内部、深部扩展的趋势，因此对于岩层的整体稳定性的破坏极大[1-2]。一旦岩层出现了不可调和的破坏，不仅影响施工进度，更严重影响了施工人员的生命安全，因此，对新景3号煤层大断面顺槽掘进的空顶距进行合理的、优化的确定十分有意义[3]。

1 工程概况

新景矿3号煤层平均埋深420m，煤尘具有爆炸性，自燃倾向性等级为容易自燃，煤层自然发火期短，井田属于地温正常区，地温梯度小于3℃/100m，无地热危害。煤层上方24.15～30.50m范围内，顶板主要由泥岩、砂质泥岩、粗粒砂岩和中粒砂岩组成，其中中粒砂岩为主体岩层，底板主要由砂质泥岩和泥岩组成[4-5]。

煤层顶底板岩性统计见表1。

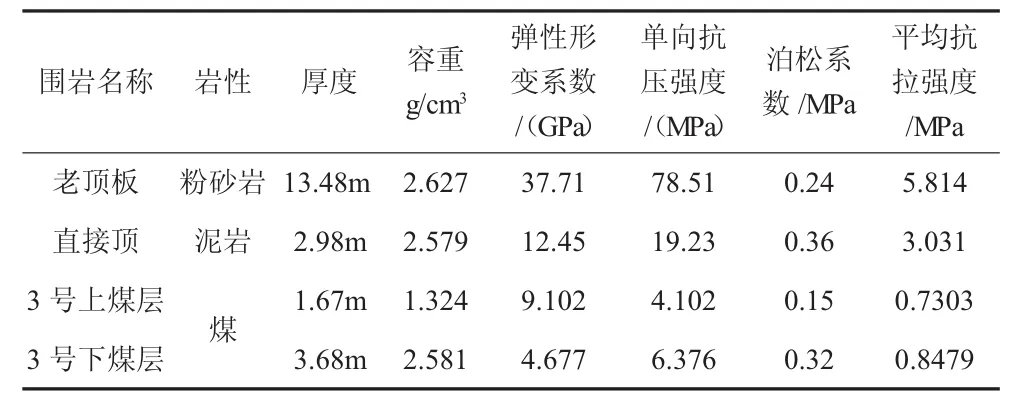
表1 巷道顶底板统计

2 顺槽掘进最大空顶距的理论推导及实际计算

将掘进煤层巷道的平面模型重画于图1中。

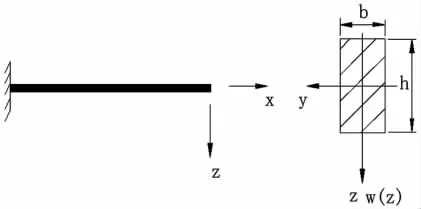
图1 煤层巷道的平面力学模型

将上述平面力学模型在宽度方向上进行扩展，可以得到煤层巷道的矩形薄板模型，如图2所示。

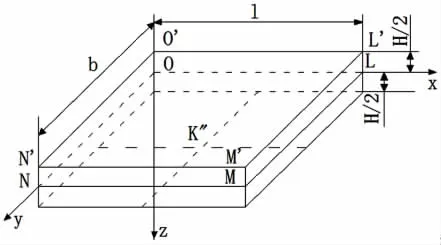
图2 煤层巷道的矩形薄板模型

2.1 顺槽掘进最大空顶距的理论推导

根据矩形薄板力学模型，可认为巷道掘进区域顶部的关键性岩层处于双向应力状态。将其视为矩形薄板后，其共有两个较长边和两个较短边。在上述四个边界中，其中三个边界可被视为处于固定铰支状态，而剩余一个边界处于简单支承状态。此外，在上述四个边界中，载荷在不同边界上均为均匀分布的切分布载荷强度可认为弯曲相同，显然载荷在长边上的积分限大于再短边上的积分限，因此两较长边上所分布的载荷应该大于两较短边上所分布的载荷。由此可见，整个矩形薄板强度的危险边界在较长边所在的边界处。因此，对上述被简化为矩形薄板的顶部关键岩层的强度校核，就是对矩形薄板的长边进行校核[6-7]。

在图2中，我们将坐标系的xy平面建立在矩形截面高度方向上的对称平面上，且坐标系的原点位于矩形的一个顶点处。基于此，矩形薄板的下表面可以由如下方程确定：

式中：h为煤层关键岩层的厚度，m。

拉应力σx的计算公式为：

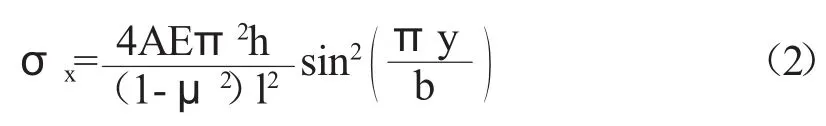
式中：l为掘进矩形断面的径向宽度，m；为煤层关键岩层的厚度，m；b为掘进矩形断面的轴向长度，m；μ为泊松比；E为板的弹性模量；

将上式对x求导得到：

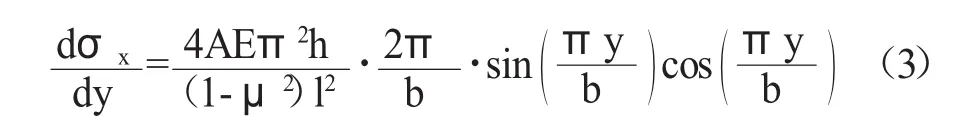
令上式等于0可解得：

将代入式（2）可得拉应力σx的极大值为：

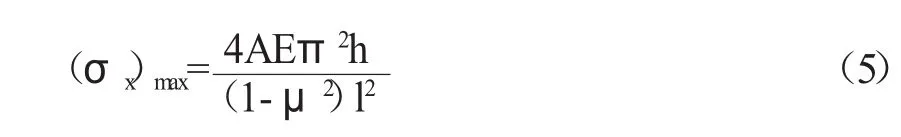
考虑到矩形截面的几何形状，并根据材料力学的知识，我们可以得到：

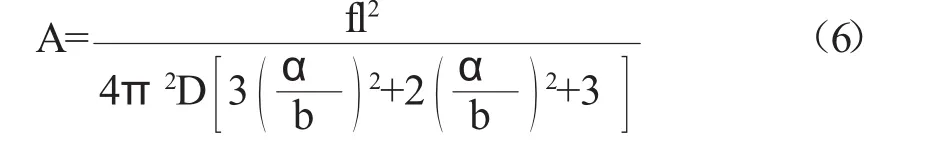
式中：D为直接顶部坍塌距，m；a为巷道宽度，m。

通过上述公式的转化，将处于拉扭组合变形应力状态的矩形截面的强度公式转换成以拉应力为主体、并加以拉扭修正系数的形式。故可根据拉应力的极限值对矩形截面强度进行校核。不妨设3号煤层的顶部关键性岩层的极限抗拉强度值为[σ]，即当拉应力σx达到极限抗拉强度值为[σ]后，此时3号煤层的顶部关键性岩层处于破坏的临界状态；当拉应力σx小于极限抗拉强度值[σ]时，3号煤层的顶部关键性岩层可认为处于稳定状态；当拉应力σx大于极限抗拉强度值[σ]时，3号煤层的顶部关键性岩层可认为处于被破坏状态。联立式（5）至式（7），并考虑临界破坏条件，代入（σx）max=[σ]解出最大空顶距bmax的理论计算值：

2.2 顺槽掘进最大空顶距的实际计算

基于对3号煤层的地质实测结果以及已知的掘进参数，可得式（8）中各参数值如表2所示。

表2 3号煤层顺槽掘进最大空顶距计算所需参数值汇总

将表2中的各参数代入式（8）中计算可得3号煤层顺槽掘进最大空顶距bmax的理论计算值为：

值得说明的是，上述最大空顶距的理论计算公式及计算结果均是在临界条件下获得的，而实际工程应用中，为了保证设计参数充分满足可靠性要求，还应将上述计算结果除以一个大于1的安全系数进行修正。在综合考虑了对3号煤层岩层为不太稳定的煤层，我们取安全系数，则修正后的最大空顶距[bmax]为：

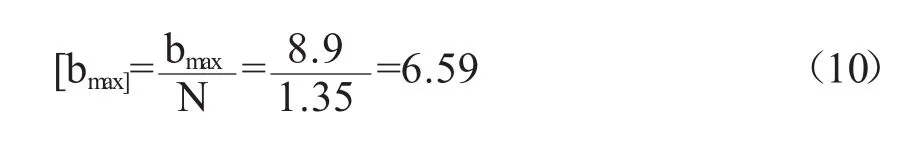
3 顺槽掘进合理空顶距的现场测定

对3号煤层进行空顶距试验，以通过实测值与理论计算值得比较，进一步从工程应用的角度检测空顶距优化结果的好坏，并以此作为前述力学模型合理性的检验标准。值得注意的是，在对3号煤层的空顶距进行优化的过程中，我们前后采用了极值理论计算和现场测试两步走的方式，这两个步骤虽然有同样的研究目标，但是却并不重复和冗余。这是因为，理论计算的结果为空顶距的理论最大值提供了参考，为最优化空顶距的现场测定提供了测试范围，缩小了现场测定时的空顶距试验范围，大大减少了空顶距现场测定时的摸索性与不确定性。作为空顶距优化的后端，现场测定不仅保证空顶距优化结果扎实落地，而且保证其确定过程不脱离实际。此外，现场测定也验证了优化结果的合理性。

3.1 空顶距优化的现场测试原理

在对3号煤层的空顶距进行优化时，我们首先选定了一段巷道，并在没有施加任何支护措施的条件下，观察其顶部岩层沉降的现象并测量沉降值。为了保证掘进断面的顶部岩层能够在无支护的自由状态下保持稳定，我们对现场测定的方法进行了改进，设计了具有保护功能的测量试验。这种保护性的测量方法将锚索和锚杆按设计的支护方式安装在巷道顶板上。锚索的一端深入稳定岩层内1m以上，另一端由承压板、塑料止挡圈和螺母。其中，塑料止挡圈位于板与螺母之间。螺母被旋紧并加载到约1kN的压紧力，以通过保证确保板和顶岩之间的有效接触。由于塑料止挡圈的抗压强度与掘进过程中的地压相比是微不足道的，因此塑料止挡圈的许用压力可以忽略不计，且此时锚索也可被看做与岩顶浮动接触，即锚索不会加强屋顶。塑料止动环的长度被设计为可以保证覆盖无任何支护作用的岩层顶部沉降的一般范围。基于此，挡圈的变化可视为屋面的地面沉降。在测定挡圈被旋紧后的初始形变后，每天测量其附加形变即可对煤层顶部进行观测。

3.2 空顶距优化的现场测试方法

3.2.1 实验锚索设计

为了保证巷道顶板下沉后还能保持稳定，又能让巷道顶板有一个自由的下沉。预防顶板事故的措施是：在巷道顶板按照设计好的间排距打上长锚索，锚索一端必须深入稳定岩层1m以上。承物盘、塑胶限位装置、锁装置共同组成锚索的另一端，塑料限位装置的作用是确保顶板与承物盘的良好相接。由于与岩压相比，塑料管道抵抗外部压力的强度要小得多，据此塑料管道的压力承载作用可以不被考虑，在这种简化的模型之下，塑料限位装置的长度即与岩层顶部自由悬空区域的长度相等。结合上述的原理，设计的锚索结构如下图：

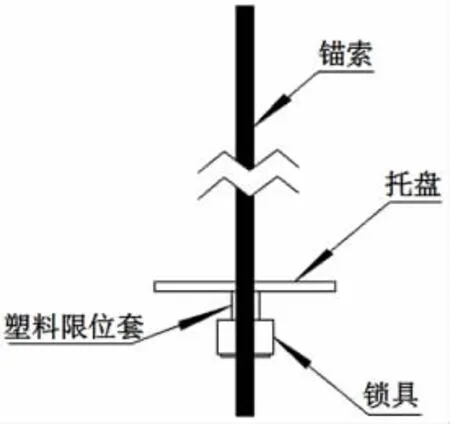
图3 试验段锚索结构图

3.2.2 空顶试验中的支护设计

根据上述空顶试验原理，试验段锚索的具体参数如下：

锚索索体：1×7低松弛钢绞线，公称直径Φ17.8mm×L8300

锚固剂：每根用1节K2335和2节Z2360

托盘：300×300×15mm

锁具：三瓣锁芯，MT17.8配套

塑料限位套：内径Φ22mm，高度40mm，厚5mm

在胶运顺槽（6m×4m）选择一个区段作为试验段，保证试验段两端都是正常支护，试验段施工完成之后必须保证巷道的正常掘进，保证试验的接近实际情况，试验段实施如下：

图4 试验段支护设计

3.2.3 空顶试验检测设计

用游标卡尺测量限位套的变形，得出巷道表面变形规律。但对顶板内部的变形还无法测得，所以得相应的在顶板内放上多点位移计，测量顶板内部的变形情况，以便详细的评价顶板的情况。在试验段都安装了多点位移计和顶板离层仪来观察顶板内部的变化。

3.2.4 巷道不同空顶距下的实验

考虑到在2.2中已经确定出的空顶距的理论最大值6.59m，又由于合理的空顶距试验值范围应包括空顶距的理论计算最大值，因此我们分别选择相应的空顶距试验值位6m和8m的空顶距进行试验。

根据3.1中的测试原理，在测试中，测量锁紧后的塑料止动环的初始值，并每天记录挡圈的形变值。挡圈的形变值即可表征巷道顶部岩层的沉降值。在五天的现场测量试验中，螺母需保持拧紧状态并保证前述的紧固压力值，以确保巷道屋顶的稳定性。挡圈的形变用精度为0.01mm的游标卡尺进行测量。在不同的空顶距下，测量的顶部岩层的沉降值如图5所示。

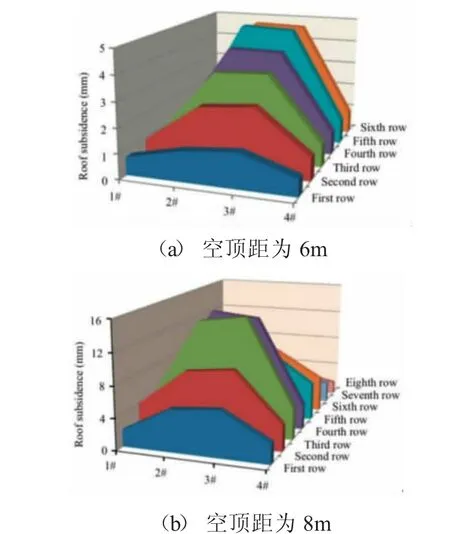
图5 不同空顶距条件下顶部岩层沉降的现场实测值

从图中不同空顶距条件下顶部岩层沉降的现场实测值曲线可以看出，2号限位套和3号限位套挡圈的形变值相对较大，使两图中的曲线均显现出梯形的形态特征。靠近肋处的1号和4号限位套的挡圈形变在不同条件下变化不大，即其形变值比较稳定。

顶部岩层的中部变形较大，且顶部岩层出现封闭肋骨的现象较少，与实际巷道开始掘进后顶部岩层形变模式相一致，显然满足空顶距试验的条件（3）。现场测试结果显示，在6m的空顶距中，掘进时的顶部岩层的应力相对稳定，与自然状态相似。但在8m的情况下，正常掘进时塑料止动圈的变形量大于顶部岩层的收缩量，顶部岩层的收缩最大值为15.11mm（约为6m空顶距的3倍）。需要指出的是，考虑到巷道顶部岩层的形变，巷道在掘进时不能一次完成8m的掘进量，必须分两次进行。综合以上，考虑到掘进过程中顶板岩层的稳定性以及施工的便利性，合理的空顶距最终确定为6m。该空顶距试验结果与理论计算值吻合得很好。