基于能力谱法、能量法和时程分析的框架结构地震响应分析

倪慧敏 焦广 王斓

摘要：本文对两个层高不同的框架结构的地震响应采用能力谱法、能量法和时程分析法分析并进行比较。对于不同的地震波，能量法的地震响应曲线包络了能力谱法和时程分析的结果，能够较准确地预测结构在地震作用下的响应值。

关键词：能力谱法;能量法;时程分析

目前抗震设计方法[1]主要有能力谱法[2]、能量法[3]、时程分析法[4]等，哪种方法能更全面的反应结构在地震作用下的抗震性能呢？本文用这几种方法对两个层高不同的框架结构分别进行分析，计算其层间位移和层间剪力，对比并得出结论。

1 能力谱法的基本原理

能力谱法采用沿结构高度呈一定分布模式的单调增加的水平荷载，计算得到结构的基底剪力与顶点位移的推覆关系的曲线，并由等效单自由度体系确定地震作用下的目标位移，进而得到结构在地震作用下的弹塑性变形需求。

其基本思想是建立两条相同基准的谱线：一条是由荷载-位移曲线转化的能力谱线，另一条是由加速度反应谱转化的需求谱线，将两条谱线放在一起，其交点定为结构抗震性能点，将性能点对应的位移和位移容许值进行比较，判断其是否满足抗震要求。

2 能量法基本原理

能量法从结构的自身能量消耗能力出发，综合考虑多种与能量有关的影响因素，对结构在地震下的安全性能作出评价。

本文基于能量平衡的框架结构抗震设计方法采用二阶段设计，与其它采用地面峰值加速度（PGA）作为地震动强度指标不同的是，本文采用地面峰值速度（PGV）作为地震动强度指标。第一阶段设计，PGV=25m/sec;第二阶段设计，PGV=50m/sec。

3 算例分析

3.1 结构模型

采用MIDAS软件设计了两个框架结构，两个结构的标准层平面和竖向布置相同，层高4m，结构1有8层，总高度32m，结构2有4层，总高度16m。设计地震烈度为8度，地震分组为第一组，II类场地。梁截面为H型截面，大小为HM582×300×12×17，，柱为箱型截面□600×20，质量取1000kg/m2。

《建筑结构荷载规范》中提出结构基本自振周期的经验公式为T=（0.10～0.15）n，经过计算，结构1的特征周期为1.158s，结构2的特征周期为0.556s，根据公式可知，结构1和结构2符合设计要求。

3.2 能力谱法分析

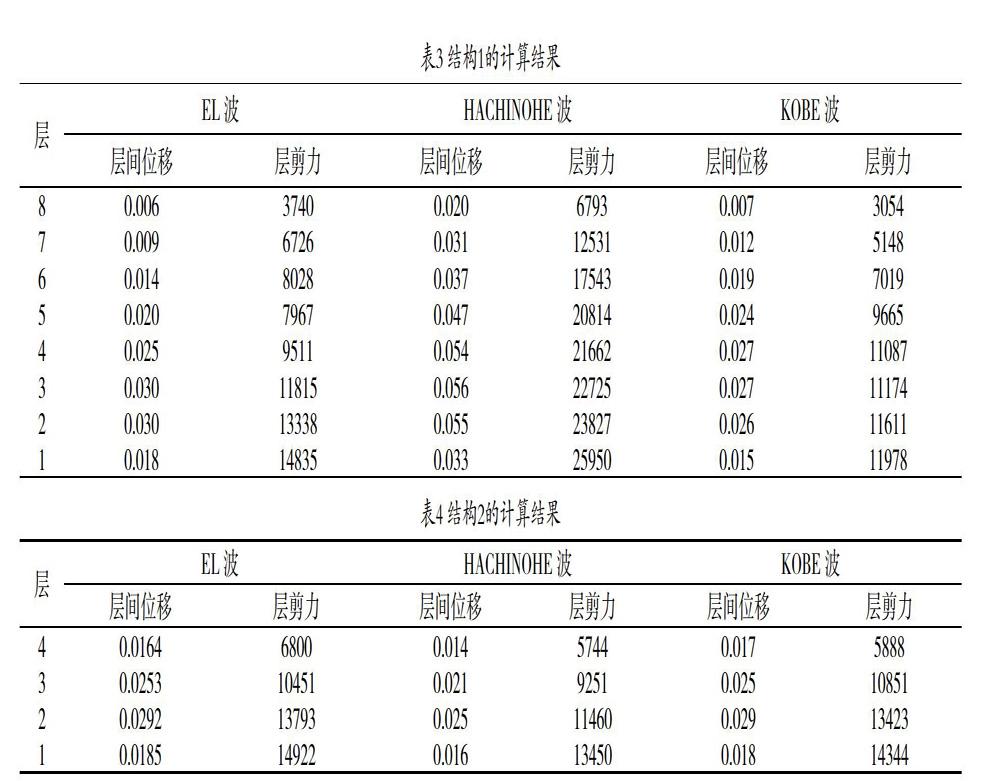
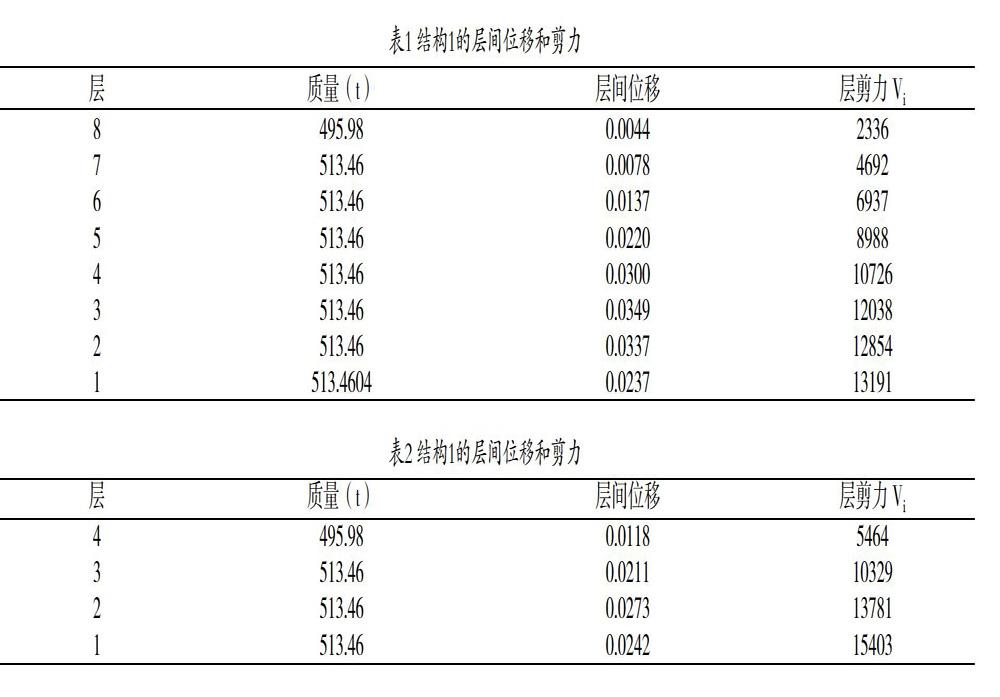
利用MIDAS软件对结构进行静力弹塑性分析，得到结构1在八度罕遇地震作用下的性能点Sa=0.3912×9.8=3.834m/s2，Sd=0.1386m，即结构1简化为单自由度体系时的加速度为3.834m/s2，位移为0.1386m。结构2在八度罕遇地震作用下的性能点Sa=0.8919×9.8=8.74m/s2，Sd=0.067m，即结构简化为单自由度体系时的加速度为8.74m/s2，位移为0.067m。根据公式计算出结构1和结构2每一层的层间位移和剪力（表1、表2）。

3.3能量法分析

对结构施加以Ai分布的水平荷载进行静力弹塑性分析，得到结构每一层的恢复力特征曲线，并对特征曲线进行二折线模拟，得到结构的损伤界限时的每层的剪力和层间位移以及安全界限时的保有水平耐力和层间位移。

计算安全界限时结构的总耗能需求和结构的累积变形耗能需求，结构各层的必要累积塑性变形倍率和最大层间位移。计算得到结构1损伤界限时地震耗能需求Ed=223kN·m和结构耗能能力We=420kN/m，Ed

3.4 时程分析

3.4.1地震波的选取

由于天然波的频谱特性对基本周期不同的结构产生的地震作用不同，而本文讨论的结构其基本周期均不同，因此，采用天然波的计算结果不具有可比性。为了避开天然波的这一特性，本文采取三条人工地震波对结构进行弹塑性时程分析。

为了得到准确的时程分析数据，与能量法计算结果有可比性，在计算每个算例模型时，调整ART EL CENTRO、ART HACHINOHE、ART KOBE波的峰值使地震波能量谱速度换算值为PGV=50m/sec。

3.4.2 计算结果及分析

（1）能量法计算的结构的每层的层间位移值几乎均大于能力谱法和时程分析法计算的相应楼层的最大层间位移值。结构1的能力谱法、ART EL CENTRO、ART KOBE波计算的层间位移值近似相等，均小于ART HACHINOHE波、能量法计算的层间位移值。结构2的能力谱法、ART EL CENTRO、ART HACHINOHE波、ART KOBE波计算的层间位移值近似相等，均小于能量法计算的层间位移值。

（2）能力谱法、能量法和时程分析法计算的每层的层间位移值的变化趋势相同。结构1的最大层间变形集中在第2、3、4层（表3），结构2的最大层间变形集中在第2层（表4）。

（3）由于时程分析计算时结构所对应的地震波能量谱速度换算值均相等（PGV=50m/sec），在不同地震波作用下，结构2各层的最大层间位移值近似相等;结构1在ART HACHINOHE波作用下最大层间位移值偏大。

根据结构1和结构2的每层的剪力和层数的关系，可以得到以下结论：

（1）结构1的能力谱法、ART EL CENTRO、ART KOBE波计算的水平剪力值近似相等，均小于ART HACHINOHE波计算的水平剪力值。结构2的能力谱法、ART EL CENTRO、ART HACHINOHE波、ART KOBE波计算的水平剪力值近似相等。

（2）能力谱法、能量法和时程分析法计算的每层的剪力的变化趋势相同。

（3）由于时程分析计算时结构所对应的地震波能量谱速度换算值均相等（PGV=50m/sec），在不同地震波作用下，结构2各层的水平剪力值近似相等;结构1在ART HACHINOHE波作用下水平剪力值偏大。

4 结论

利用能力谱法、能量法和时程分析法分别计算了两个层高不同的框架结构的地震响应值，将其计算结果进行了比较分析，得到以下结论：（1）能量法计算的结构的最大层间位移值能够包络能力谱法和时程分析法计算的最大层间位移值。（2）能力谱法、能量法和时程分析法计算的结构的最大层間位移值和每层的剪力的变化趋势相同。（3） 对于层高不高的结构，能力谱法和时程分析法计算的结构的最大层间位移值和每层的剪力近似相等。

参考文献：

[1] Housner G. Limit design of structures to resist earthquakes[A].Proceedings of the 1st World Conference on Earthquake Engineering[C].Oakland，Califormia：1956：1～12

[2]Fajfar， Peter. Capacity spectrum method based on inelastic demand spectra[J].Earthquake Engineering & Structural Dynamics，1999，28（9）：979-993.

[3]黄宗明，白绍良，赖明.结构非弹性地震能量反应的分析方法[C].第三届全国结构工程学术会议论文集（下），1994：159-166.

[4]程绍革，王理，张允顺.弹塑性时程分析方法及其应用[J].建筑结构学报，2000（01）：52-56.