基于教科书中的阅读材料,合理创设问题情境
2020-06-25昆明高新区第三中学云南省高中数学于雷名师工作坊唐明超
昆明高新区第三中学 云南省高中数学于雷名师工作坊 唐明超
2019 年12 月进行的云南师大附中2020 届高考数学第五次模拟测试第20 题是一道圆锥曲线题,由于学生的得分情况不理想而引起笔者的高度关注.经过与学生交流,笔者发现,学生学习完圆锥曲线的新课后,对椭圆具有“从一个焦点发出的光线经椭圆反射后,反射光线一定经过椭圆的另一个焦点”这一性质有一定的印象,而且在平时的练习中也碰到过直接利用该性质求解的相关试题,但是大多数学生却不清楚该性质背后的数学本质以及该性质的证明方法,导致他们在有限的考试时间内无法完成对这类问题的思考与正确解答.基于此,笔者决定就该问题开展微专题教学,拟定课题名称为《圆锥曲线的光学性质及其应用》.
1.教学内容及目标.
基于学生的实际学情,结合课程标准的相关要求,将本节课的教学内容及教学目标拟定为认识圆锥曲线的光学性质,掌握圆锥曲线光学性质的证明方法,能运用该性质解决一些实际问题.
2.教学内容与素养发展的关系.
通过阅读材料提取关键信息,将文字语言转化为数学语言,能够很好地发展学生的数学抽象核心素养以及数学表达能力;基于数量关系与图形特征构建合适的数学模型,能够发展学生的数学建模核心素养以及用数学思维思考问题的意识;合理运用已有知识经验证明该性质的过程可以有效地发展学生的逻辑推理与数学运算核心素养.
3.素材选取.
由于圆锥曲线的光学性质在普通高中人教A 版实验教科书选修2-1 第75 页“阅读与思考——圆锥曲线的光学性质及其应用”一栏中有介绍,笔者将其选定为教学情境创设的素材,给学生布置课前自主学习任务,要求学生认真阅读素材并提取关键信息.
4.情境创设.
将上述阅读材料作为本节课的生活情境,引入课题.为了帮助学生提高自主学习效果,笔者特地设置了以下问题情境,目的在于给定指向明确的问题,让学生弄清学习任务,并带着问题去阅读材料,寻找关键信息.
问题1:认真阅读材料并提炼出电影放映机、探照灯、太阳灶的设计原理.
问题2:用数学语言描述电影放映机、探照灯、太阳灶的设计原理.
问题3:你能尝试用数学知识证明这些原理吗?能找到几种证明方法?
教师引导学生归纳总结自主学习成果,得出以下三条圆锥曲线的光学性质:
性质1:从椭圆的一个焦点发出的光线经椭圆反射后,反射光线都经过椭圆的另一个焦点.
性质2:从双曲线的一个焦点发出的光线,经双曲线反射后,反射光线是散开的,就好像是从另一个焦点射出的一样,也就是说,反射光线的反向延长线经过另外一个焦点.
性质3:从抛物线的焦点发出的光,经抛物线反射后,反射光线都平行于抛物线的对称轴.
5.提出问题.
问题4:请展示一下你们的证明思路.
6.解决问题.
受思维定式的影响,大多数同学使用解析法进行证明,即证明其中一个焦点关于切线的对称点,在过切点与另一个焦点的直线上.具体证明过程如下.
性质1 证明(解析法):如图1,设直线l 是过椭圆上除顶点外的任意一点P(x0,y0)的切线,切线l 的方程为.设F2关于l 的对称点为C(x1,y1),则F2C 的中点P1在直线l 上,且直线F2C 与l 垂直.解得.同理,,∴C,P,F1三点共线.∴从F2发出的光线F2P 经直线l 反射后经过F1.
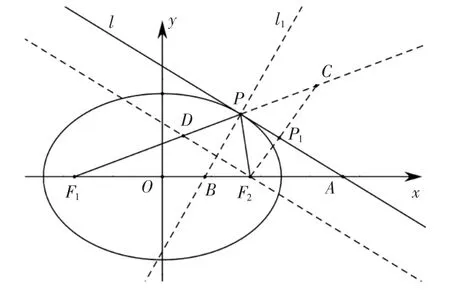
图1
性质2证明(解析法):如图2,设直线l 的是过双曲线上除顶点外的任意一点P(x0,y0)的切线,切线l 的方程为.求出焦点F2关于切线l 的对称点C(x1,y1),计算,经计算可知.原问题得证.
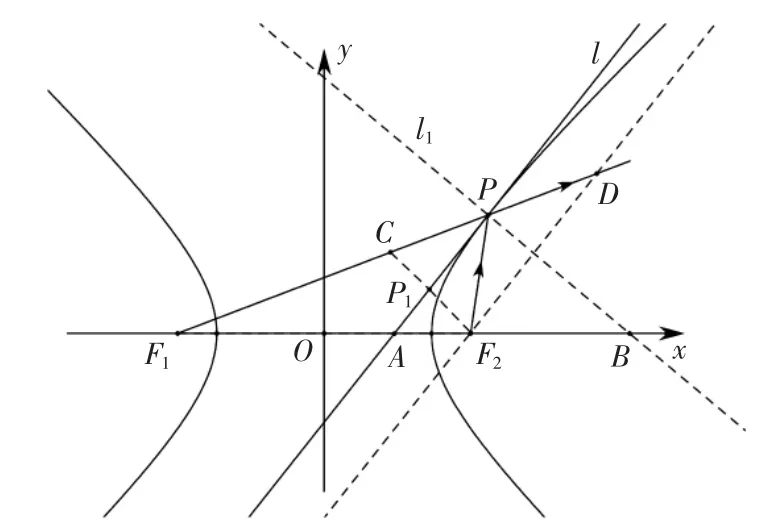
图2
性质3证明(解析法):如图3,设直线l 是过抛物线上除顶点外任意一点P(x0,y0)的切线,切线l 的方程为y0y=p(x+x0).求出焦点关于切线l 的对称点A(x1,y1),进而可以计算出,∴反射光线平行于x 轴.原问题得证.
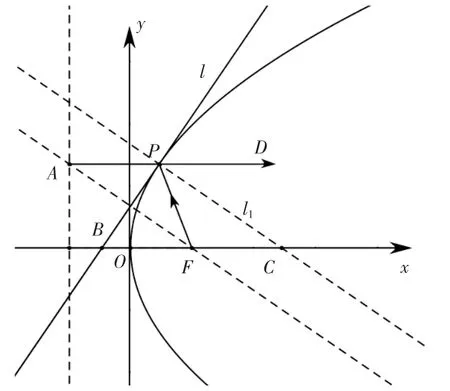
图3
问题5:同学们还能找出其他的证明方法吗?
学生1:如图1 所示,在刚才的证明过程中,我们还可以先求出一个焦点F2关于切线l 的垂线(法线)l1的对称点D,再证明点D 在过切点与另一个焦点的直线PF1上.
学生2:材料中提示可以用导数法来证明,由此我们可以先求出切线方程,再根据垂直关系得出法线方程,最后再证明入射角等于反射角,即可使原问题得证.具体证明方法如下.
性质3证明:对抛物线C 的方程求导,得yy'=p.∴切线的斜率,法线的斜率∴由到角公式,得将代入,得tan∠FPC∴tan∠DPC=tan∠FPC,即∠DPC=∠FPC.原问题得证.
学生3:不用到角公式也可以证,结合几何性质,利用两点间的距离公式也可以得出答案.对于性质1 及性质2的证明,我们只需要证明PD=PF2或证明PC=PF2即可;对于性质3 的证明,我们只需要先证PF=PD 或PF=BF,均能得出入射角等于反射角.
解法点评:以上的解决问题的方法各有优劣.解析法容易想,但运算很复杂;导数法相对简便,但求导的过程容易出错.两种思路都或多或少用到了几何性质,但都没有用到定义,因此教师还可以引导学生基于定义寻找证明该性质的方法,由于课堂探究时间有限,笔者将其设置成了课后拓展作业.
课后作业:通过交流、查阅文献,寻找一种不同于解析法和导数法的证明方法,清楚地写出证明过程.
7.教学反思.
问题来源于教学实际,自然而然;素材选自课本,追本溯源.基于教科书中的阅读材料合理创设问题情境,引导学生发现问题、提出问题、思考并解决问题,可以有效利用高中数学教科书中的阅读材料辅助教学,达到用活教材、开发教材潜能的目的,从而可以更好地服务教学,提高课堂教学的质量,发展学生的数学核心素养.在整个探究活动中,学生作为学习主体,经历了阅读材料并提取关键信息,将问题情境数学化、数量与几何关系模型化,再基于元认知发展水平用数学思维思考并解决问题的整个过程,可以帮助学生更好地理解数学问题的本质、发展学生的探究能力,积累有益于学生个体发展的学习经验,逐步形成用数学的眼光观察世界、用数学的思维思考世界、用数学的语言表达世界的重要能力.
