顶旋泵轻量化转子的型线构造及性能分析

（宿迁学院，江苏宿迁 223800）

0 引言

罗茨泵作为一种非接触式凸转子泵，广泛应用于真空、抽风、鼓风、水油搬运等领域。其中，主、从转子的型线与尺寸完全一致，圆弧[1]、渐开线[2]、摆线[3]是目前最为常见的 3种型线类型，对应的转子称为常规转子，其具有以下共性特点：（1）承担转子副本体运动的一对顶部、谷部工作型线段相接于节圆的两侧，（2）转子顶与泵壳间为“顶轴向线—壳腔圆弧面”的孔隙，径向孔口泄漏大[1-3]。顶旋泵（Epitrochoidal Lobe Pump）正好相反，工作型线段位于转子顶部，顶旋泵也由此得名，且形成相对小泄漏的径向缝隙。自顶旋转子因恒流被提出以来[4]，国内外展开的研究还不多[5]。因此，拟就顶旋转子的轻量化型线构造及性能作进一步研究与分析。

1 顶旋泵的叶型线构造

转子型线均由节圆内、外的谷、顶两部分型线段组成，记转子叶的顶、谷部的对称轴为顶轴和谷轴如图1所示。其中，顶型线为顶圆弧段，谷型线为谷圆弧段，两者间为过渡曲线段。

图1 顶旋转子泵的叶型线构造

顶圆弧段与谷圆弧段共同构成了转子副的本体共轭运动，则，顶圆弧段圆心角=谷圆弧段圆心角=π/N，其中，N为转子叶数，而过渡曲线段由顶圆弧的端点扫掠而成，不参与转子的本体共轭运动。

设转子的形状系数为ε，节圆半径为r，则顶圆弧半径ra、谷圆弧半径rb分别为：

2 顶旋泵的轻量化指标

采用扫过面积法考察泵流量的情况。图2中，设在微小时间dt内，主、从转子o1，o2的顶径ra1，ra21转过dω微小角度；而主转子谷径rb1、从转子顶径ra22因始终共轭在o1o2线上，其转过的微小角度为0。此时，主、从转子的两顶圆弧段ra1、ra21、泵进口轮廓线、主转子谷圆弧段rb1、从转子顶圆弧段ra22和壳腔圆弧封闭围成图2剖面线所示的截面积，其对应的微小容积变化量dV为：

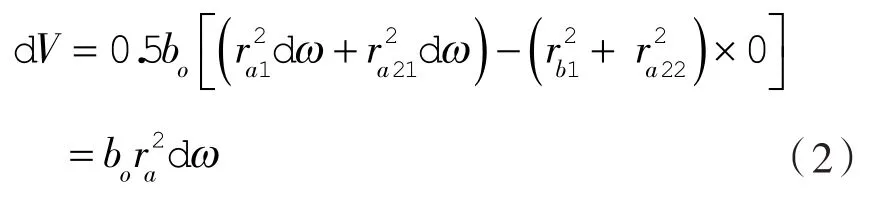
式中 bo——转子的宽度。

由上式可知，顶旋泵为恒流泵，流量脉动为0。

设泵的排量为qs，容积效率为ηs，转速为n，转子轴向截面积占转子腔轴向截面积的百分比为ηrotor，容积利用系数为λ=1-ηrotor，内泄漏率为ηleakage，转子腔的空间以双转子的顶圆柱腔体积Vcavity=2×πra2bo来表示。则由：

得：

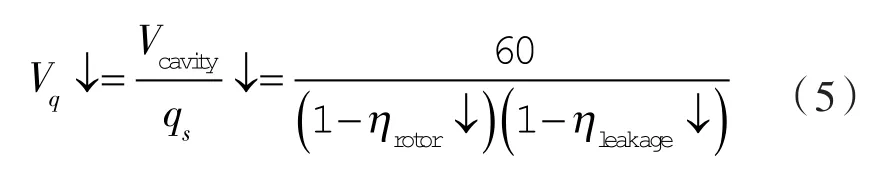
式中 Vq——泵的单位排量体积[6-10]，即轻量化指标。

由式（4）可知，ηrotor↓和ηleakage↓进而Vq↓。现有研究结果表明，ε主要决定单位节圆半径下转子的型线类型[1-3]，独立于节圆半径r的大小。而ra最大化等价于ε最大化和r最大化，且r↑进而ηleakage↓，且r最大化主要由ε最大化结合泵额定流量加以计算[6]。因此，泵轻量化程度取决于形状系数最大化，下面仅就形状系数ε的影响加以分析。

图2 流量计算的扫过面积法

3 顶旋泵的叶型线方程

以主从转子的顶、谷圆弧端点 a1（b2）、b1（a2）均共轭于中心线o1o2上的位置，作为转子副旋转的起始位置，如图3（a）所示，并以顶轴为y轴，o1为原点，构建xo1y直角坐标系。以顶圆弧端点a1、a2接触的位置，作为旋转的终止位置，如图3（b）所示，对应的转角为ωa之间的任一位置，如图3（c）所示，所对应的转角为ω∈[0，ωa]。

图3 过渡曲线扫掠的生成过程

图（b）中，由a1（a2）在中心线 o1o2上的垂足为o1o2的中点，即节点，得：

图3（c）中，设σ=∠a2o1a1，∠yo1a2=φ，令

式中 t——0～1间的变量。

由⊿o1a2o2几何关系可得：

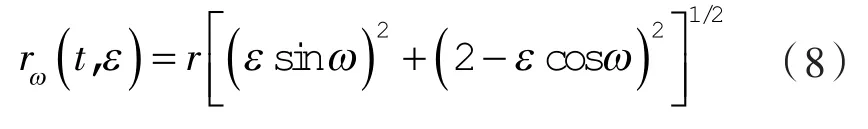
式中 rω——o1a2的长度。

得

式中 （xω，yω）——过渡曲线段在 xo1y中的参数化坐标；

（xa-arc，ya-arc）——顶半圆弧段、谷半圆弧段在xo1y中的参数化坐标；

（xb-arc，yb-arc）——谷半圆弧段在 xo1y 中的参数化坐标。

4 最大形状系数及参数化模型

由图3可以看出叶最薄弱截面应位于σ最大的地方，如图3（a）所示，设对应的最薄弱圆弧（定义为根圆弧）的圆心半角（定义为根圆半角）为β。为此，构建目标函数：β（t）↓；设计变量：t；约束函数：0＜t＜1的优化模型，得对应于β最小化的 t*（ε）和σ（t*，ε）、rω/r（t*，ε）、β（t*，ε，N），如表1所示。其中，β（t*，ε，N）=φ（N）-σ（t*，ε）。

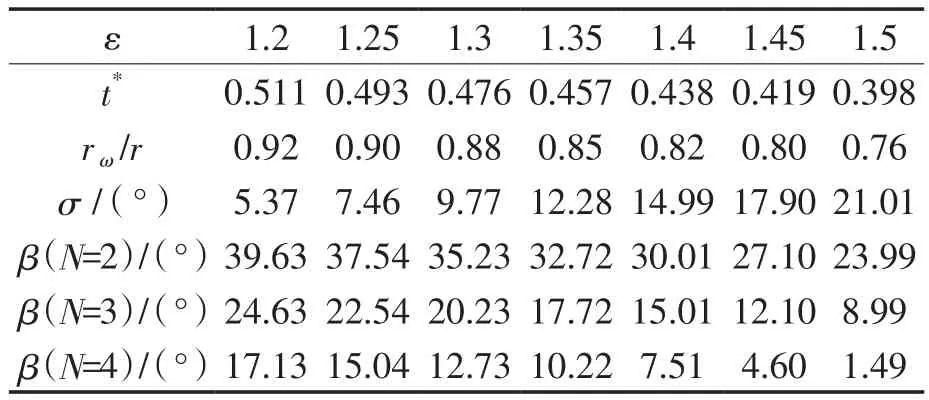
表1 不同叶数、不同形状系数下的最薄弱截面几何

由表1知，ε↑→rω/r（ε）↓，ε↑→φ-σ（ε）↓。前者表示最薄弱截面越接近根部，后者表示最薄弱截面宽度越窄，均减弱了转子叶的抗弯曲能力。N↑→φ-σ（N）↓，表示叶数越多，转子叶的抗弯曲能力越弱。

在保证足够的拟合精度下，β（ε，N）的拟合方程为：

设[β]为β（ε，N）的最小根圆半角，则由

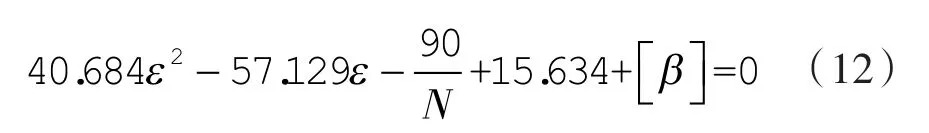
得最大形状系数为：

[β]=0时有 N 为2，3，4时 εmax分别为1.804，1.622，1.516。

[β]=0实际上不存在，这里仅为比较用。

ε=1.4时转子对应的3D参数化模型如图4所示。同样可以看出N↑→β（N）↓→抗弯能力↓。

图4 不同叶数的参数化转子副

5 容积利用系数及拟合方程

由式（10）的叶型线方程构建3D转子模型，通过3D软件的面分析功能，分别测出不同叶数、不同形状系数的转子轴向截面积srotor，并由：

计算得到的容积利用系数λ，如表2所示。其中，ε↑→λ（ε）↑；N↑→λ（N）↑。前者与常规转子一样；但后者却相反。

表2 不同叶数、不同形状系数下的容积利用系数

λ（ε，N）的拟合方程为：

6 闭气现象及简化加工方案

在图3（c）中，由于过渡曲线由顶圆弧的端点a2扫掠而成，自然就形成如图3（c）中剖面线所示的2个分割区域，从而产生类似于齿轮泵“困油现象”的“闭气现象”。为消除该现象和利于过渡曲线的加工，提出了一款简化的结构方案，如图5所示。

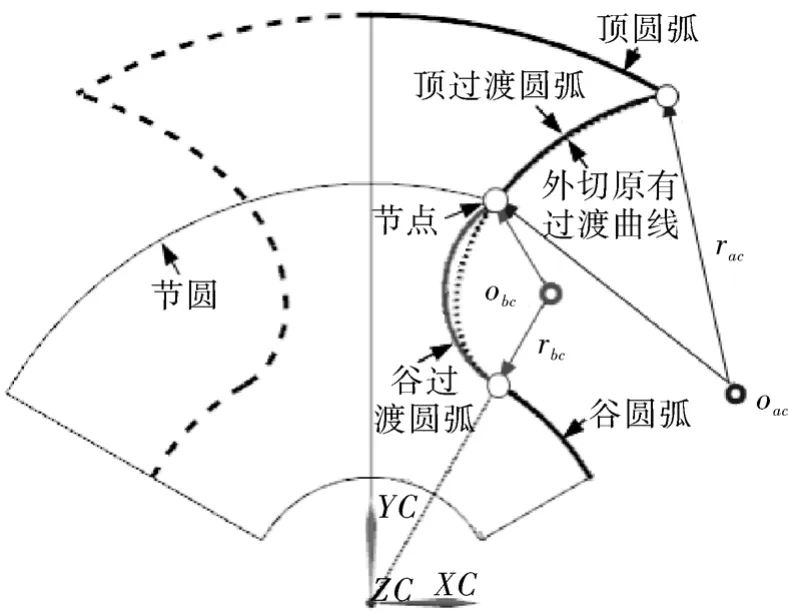
图5 扫掠过渡曲线的圆弧简化

由于过渡曲线不参与转子副的本体工作运动，对其的光滑连续性没有特别要求，所以，可以采用两段圆弧来简化加工及消除“闭气现象”。其中，谷过渡圆弧圆心obc及半径rbc由过谷圆弧端点且外切谷圆弧段，另一端点与原有过渡曲线与节圆的交点（即节点）的三点几何条件唯一确定；顶过渡圆弧圆心oac及半径以rac由过顶圆弧段端点和节点，且外切顶部过渡曲线的三点几何条件唯一确定。由此，该转子的半叶型线有4段圆弧构成，虽然该方案增加了余隙容积，但并不构成对原有可利用容积系数的影响。

7 结论

（1）顶旋转子的过渡曲线段分布在节圆的两近侧，共轭工作型线段位于两圆侧，具有零流量脉动、小径向泄漏优点。

（2）泵轻量化程度取决于转子顶径的最大化，顶径最大化取决于形状系数最大化，所建立的形状系数最大化公式依据叶数及根圆弧强度条件可直接采用。

（3）叶数越多，最大形状系数越小，但容积利用系数却越大，后者与常规转子的容积利用系数越小正好相反。所建立的容积利用系数拟合公式可直接采用。

（4）过渡曲线的2段简化圆弧，利于消除“闭气现象”和简化加工。