高速列车受电弓不同姿态下气动特性分析
2020-06-23刘晓禹王益鹤
赵 萌, 刘晓禹, 贾 彦*, 王益鹤
(1.内蒙古工业大学能源与动力工程学院,呼和浩特,010051;2.北京城建亚泰建设集团有限公司,北京 100013)
高速列车获得动力来源的重要集电原件是安装在列车顶部的受电弓,由于复杂的结构外形,导致其具有强烈的气流扰动[1],同时橫风作用下增强了受电弓纵向扰动,甚至会产生严重的弓网事故[2]。中外专家学者对高速列车受电弓气动特性做了大量的分析研究[3-4]。Navik等[4]采用数值模拟与实验的方法研究受电弓与接触网之间的受力关系;Song等[5]是在强横风作用下,对高速列车组件绕流场进行研究;但其中受电弓、转向架等结构经过简化,不能够精细反映列车的真实气动特性。
受电弓在开口姿态时高速气流首先绕流滑板及其附件,而在闭姿态时上臂杆尾流流场对滑板及支架产生显著影响,因此十分有必要对比分析。但是目前中外学者对于不同姿态下受电弓绕流场的分析较少,尤其是在橫风的作用下[5-7]。故针对受电弓以及弓网系统运行状态,建立模型分析在横风作用下受电弓开口姿态与闭口姿态运行时的气动特性,为进一步提高高速列车的安全行驶提供依据。
1 数值模拟方法
1.1 分离涡(DES)方法
数值模拟采用分离涡(detached-eddy simulation,DES)模拟方法,其主要方法是将大涡模拟方法与雷诺时均方法相结合[8]。选取湍流模型为SSTk-ω模型。SSTk-ω模型的输运方程的表达式[9-10]为
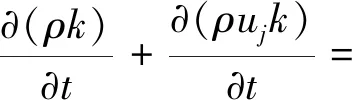
(1)
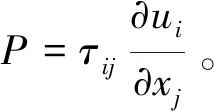

(2)
1.2 计算方法的验证
受电弓由各杆件构成,其中上臂、下臂、拉杆、底座等部件均可近似认为是钝体。

图1 Ahmed几何模型Fig.1 The model of Ahmed
Ahmed钝体绕流现已有较为深入的研究结论[11],为验证数值模拟方法的准确性,采用DES方法来对Ahmed钝体进行数值模拟研究[12-13]。
选用的Ahmed模型如图1所示,其数值模拟的边界条件为:速度入口,压力出口;入口速度为60 m/s,且钝体表面无滑移,计算域和网格的划分如图2、图3所示。

图2 Ahmed钝体的计算域Fig.2 Computing domain of Ahmed bluff body

图3 Ahmed钝体的网格划分Fig.3 Meshing of Ahmed bluff body
Ahmed钝体表面压力分布、尾部涡量分布如图4、图5所示。计算所得阻力系数Cd、摩擦阻力系数Cr分别与文献[14]中实验值进行对比研究。其中实验中阻力系数Cd=0.285,摩擦阻力系数Cr=0.055,本次数值模拟Cd=0.282、Cr=0.054,误差分别为1.05%、1.82%。由此可见,本文结果与文献[14]结果误差在合理的范围内,说明DES方法的适用性与准确性。

图4 表面压力云图Fig.4 Pressure on buff body

图5 尾部涡量线图Fig.5 Vorticity after buff body
2 计算模型和条件
2.1 受电弓模型
受电弓结构复杂,而重点研究的是受电弓主体的绕流场特性,所以对受电弓结构进行适当简化,如图6所示。图7为受电弓不同姿态运行的示意图。
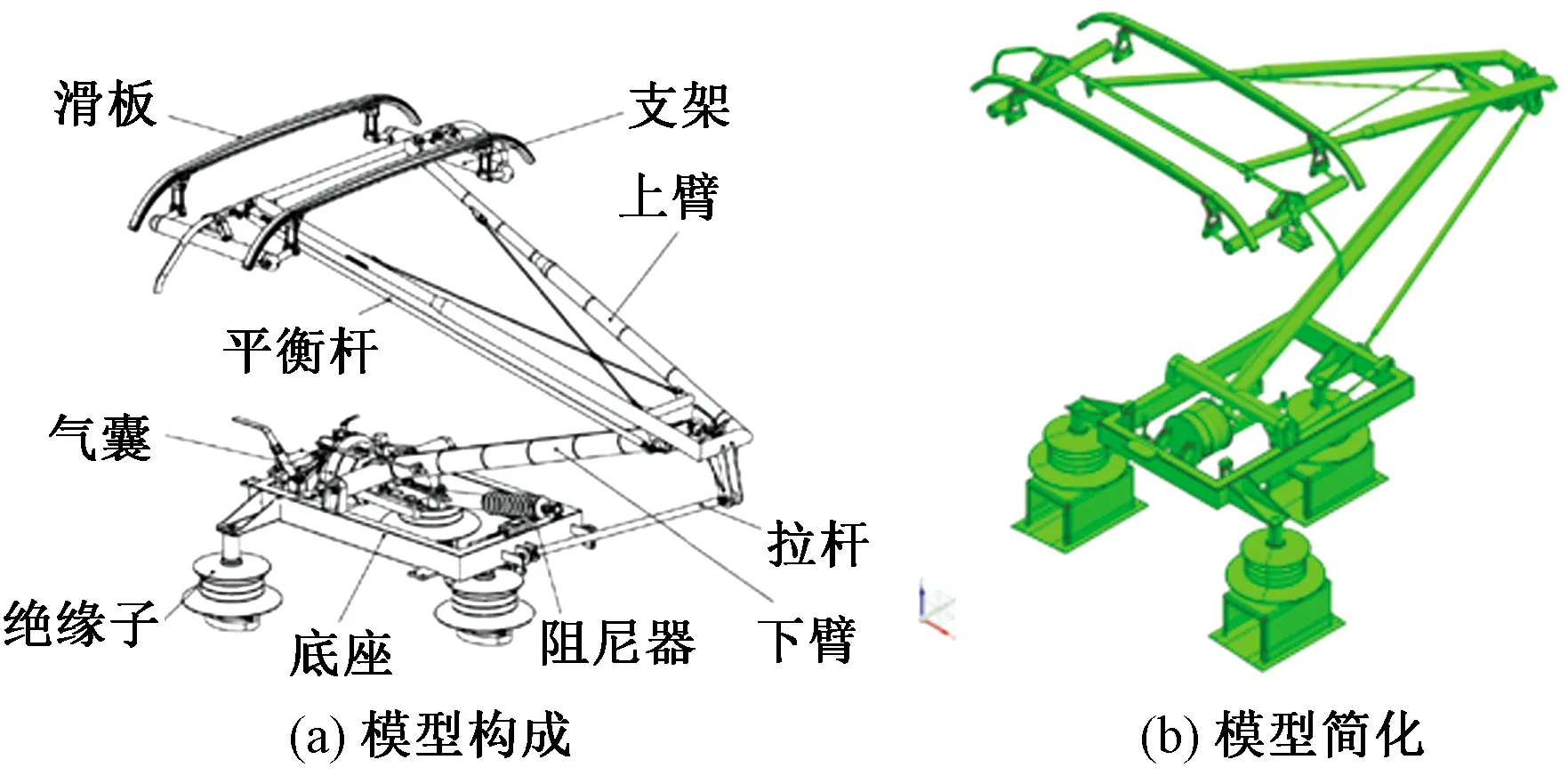
图6 受电弓模型Fig.6 The composition of the pantograph

图7 模型及计算域 Fig.7 Model and calculation domain
2.2 计算域和计算条件
采用1∶1的尺寸建立动车组受电弓-列车-接触网系统模型,接触线距地面6 m。受电弓运行时,由于其流场受到列车与网的干扰,因此采用3节车厢编组的列车模型,其中设定受电弓位于列车的中车,计算域如图8所示。

图8 受电弓不同姿态下运行示意图Fig.8 Diagram of pantograph in open and closed operation
采用六面体网格,模型边界层分为6层,以确保边界与主流区的网格平滑衔接。在重点研究区域(受电弓附近流场)进行网格加密,网格总数为750万,网格划分如图9所示。边界条件为入口速度:受电弓运行速度为350 km/h,橫风风速为15 m/s(风向角90°),出口为压力出口,相对大气压0 Pa。

图9 网格的划分Fig.9 Mesh generation
3 外流场的非定常特性
3.1 速度场与压力场的分布规律
相对于受电弓闭口姿态而言,开口姿态工况中速度矢量偏转集中在弓头区域,尤其是在弓、网相互接触的区域后方。下臂附近流场区域内速度矢量有偏转但无明显回流,其原因是受到拉杆绕流的影响较小,如图10、图11所示。
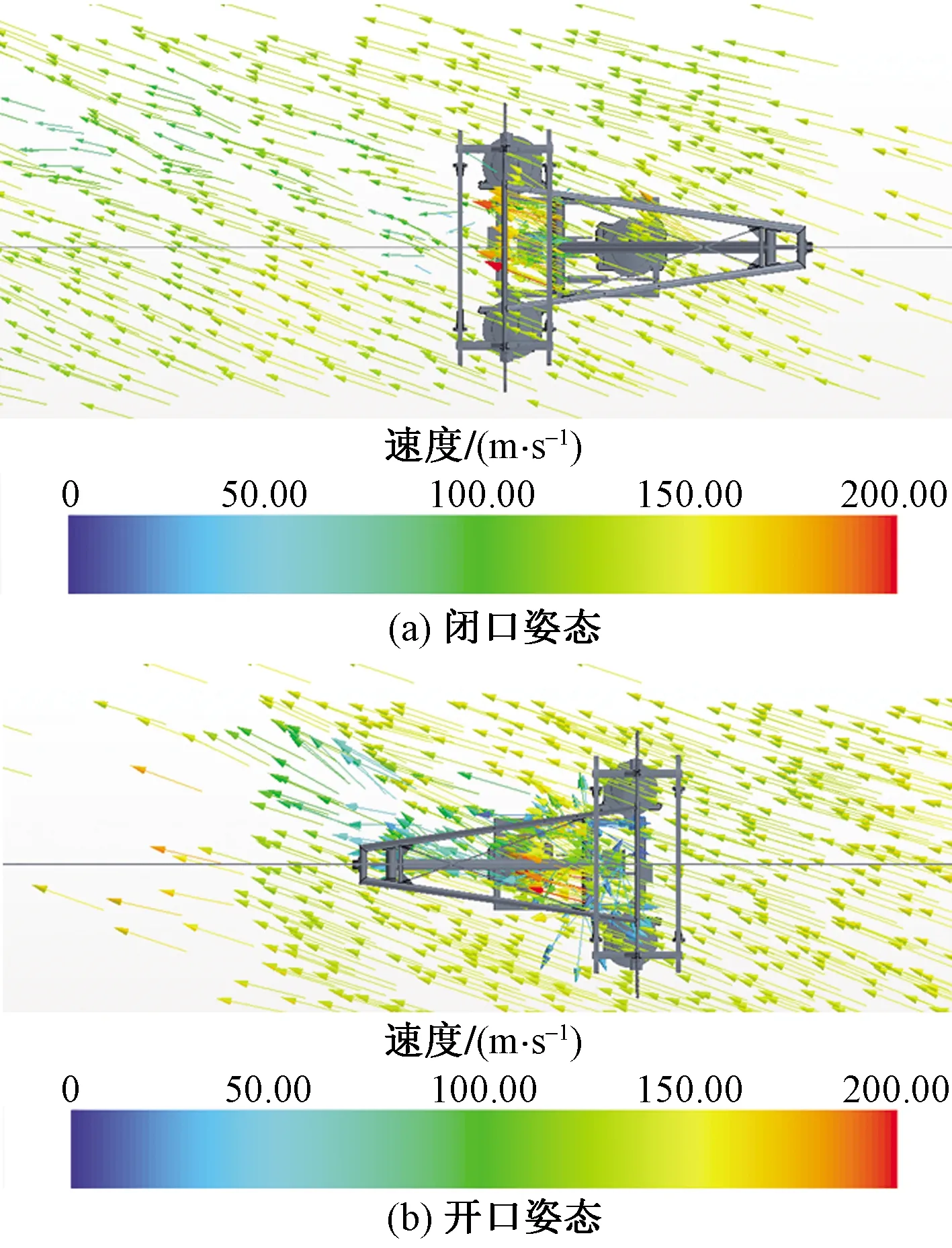
图11 水平面速度矢量图Fig.11 Velocity vector on the horizontal plane
开口姿态下,车厢之间连接处与导流板相比,后者将对绕流场造成更大扰动。根据速度矢量图可得,来流在受电弓底座及下臂底端速度矢量偏转较小,即开口姿态时受电弓底部区域受到影响较小。
开口姿态下,车厢之间连接处与导流板相比,后者将对绕流场造成更大扰动。根据速度矢量图可得,来流在受电弓底座及下臂底端速度矢量偏转较小,即开口姿态时受电弓底部区域受到影响较小。

图12 速度云图Fig.12 Velocity on the symmetry plane
图12所示为受电弓不同运行姿态下的速度云图。在闭口姿态中,导流板尾流区域对受电弓底座的影响更加显著,而开口姿态中的低速尾流主要集中在下臂和拉杆的底端。对比不同姿态下绕流场的流线分布(图13),其中开口姿态对流场扰动较小,大范围的低速尾流区域主要集中在受电弓与网接触区域的后方,这是由于受电弓部件之间与接触网绕流场的叠加效应。由此可得,开口姿态下,滑板与接触网更容易受来流影响。

图13 受电弓表面压力和流线图Fig.13 Pressure on the pantograph surface and streamline around the pantograph
3.2 涡量场分布规律
图14所示为受电弓闭口、开口姿态下的涡量分布。由图14可见,开口姿态下来流对绕流场的扰动较小,主要扰动区域为弓-网和弓-车接触区域,其中弓-车接触区域的扰动主要源自于车厢连接处对来流的影响,拉杆处于下臂的尾流区域内,由图可见,其尾流区域并没有对弓-车接触区域流场产生明显的影响。

图14 受电弓等值面图Fig.14 Iso surface around the pantograph
在开口姿态下,受电弓尾流对导流板附近流场产生显著影响;而闭口姿态下,由于导流板尾流影响以及受电弓各个部件之间的相互影响,将导致弓-网-车绕流场复杂的叠加效应。
4 气动载荷特性分析
不同姿态下受电弓绕流场受到导流板以及列车顶部的强烈扰动,从而对受电弓气动特性产生剧烈影响。因此需要分析受电弓的气动载荷特性,包括阻力系数Cx、升力系数Cy、侧向力系数Cz、倾覆力矩系数Mx、俯仰力矩系数My、侧偏力矩系数Mz。
4.1 气动力特性分析
图15~图17所示为受电弓闭口姿态与开口姿态时的Cx、Cy、Cz的时域变化曲线。

图15 阻力系数CxFig.15 Drag force coefficient

图16 侧向力系数CzFig.16 Lateral force coefficient
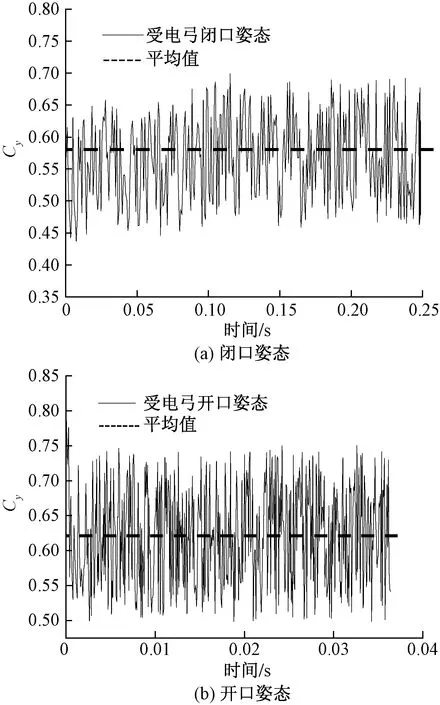
图17 升力系数CyFig.17 Lift force coefficient
当受电弓以闭口姿态运行时,即Cz完成一个周期的时长小于Cx所需时长。由此可知Cy具有较高的峰值,其原因是列车顶部区域的流场涡结构较为复杂,使Cy振荡周期的规律性增强,波动值在145%左右。
开口姿态下,Cx的平均值为0.893,其波动值为44.9%,均大于闭口姿态;Cy与Cx趋势基本相同,但其波动值仅为闭口姿态的30.2%,其峰值相对于闭口姿态增加了43.2%,且完成一个波动所需时间更长。由此可见,高速列车受电弓开口姿态下有更加强烈纵向振动。
4.2 气动力矩系数的时域特性
图18~图20所示为受电弓不同姿态运行时的倾覆力矩系数Mx、俯仰力矩系数My、侧偏力矩系数Mz变化规律。

图18 倾覆力矩系数MxFig.18 Upsetting moment coefficient Mx

图19 俯仰力矩系数MyFig. 19 Pitching moment coefficient My
在闭口姿态运行时,Mx和Mz的波动为42%,My为46.5%,其中Mx完成一个周期变化所需的时程最短。相对于闭口姿态,受电弓在开口姿态下Mx随时间的发展逐渐下降并稳定振荡在平均值附近,其最值和平均值均较大;My与Mx具有同样发展趋势,且周期变化所需时程小于闭口姿态,沿时程变化规律更具周期性且振荡周期明显减小。

图20 侧偏力矩系数MzFig.20 Deflection moment coefficient Mz
受电弓开口姿态运行时Mz的时程变化规律与闭口姿态基本一致,但波动值较小。
4.3 气动荷载的频域特性
表1所示为受电弓不同姿态下气动特性的频域变化规律。由此可得,在频率0~25 Hz的范围内,气动力系数迅速衰减,最终稳定于峰值的2.5%~25%,说明横风效应导致的受电弓非定常气动荷载主值的频率降低。
开口姿态下,在0~15 Hz的频段内,Cx的振幅值减小为峰值的28.4%,Cy减小为44%,Cz减小为29.4%;同理在0~50 Hz的频段内,Cx减小为峰值的1.5%,Cy减小为7.3%,Cz则是12.8%;由于Cz的频段较宽,说明相对于受电弓闭口姿态,横风对开口姿态绕流场特性的作用更加显著。

表1 不同姿态运行时受电弓气动荷载频域特性Table 1 Frequency domain of aerodynamic load of pantograph in open and closed operation

表2 不同姿态运行时受电弓对比Table 2 Comparison of pantograph in different operation
由表1可得,开口姿态运行时,气动力矩系数的频域宽度较大,Mx、Mz的减小速度最快,在0~100 Hz的范围内My减小为最大峰值的43.5%,该频段内Mz振幅峰值则减小为最大峰值的20%。当受电弓以闭口姿态运行时,My的频谱比Mx和Mz的要宽。这说明由于横风的存在,受电弓沿纵向振动,其自身频率耦合的范围更宽,其危险性更大。
4.4 对比分析
表2所示为受电弓不同姿态运行时气动力系数以及力矩系数的各个参数变化。在开口姿态中Cx、Cz的波动值相差3%,Cy的波动值仅为对应闭口姿态的30%,而Cx和Cz的平均值增加了8.3%和10%。由于Cy的平均值较大,结合Cy一个周期对应的时程和振幅对应的频段分析。
在开口姿态下My、Mz的平均值分别增幅为6.7%和2.3%,其波动量也分别增加了13.6%和7.2%;相比较而言,Mx平均值增加了3%,其波动值也大幅增加为相对工况的1.5倍;Mz的波动值相对较小,但振幅对应的频段较宽,高频特性较为明显,频率衰减的速度慢。
5 结论
(1)通过对受电弓不同姿态运行时的绕流场研究,可以得出受电弓的底座和下臂部分流场区域在闭口姿态下有强烈扰动;而在开口姿态时,滑板和上臂部分流场区域受到较强扰动,而车厢连接处至受电弓迎流面的区域涡量较小,底座附近的涡量小于闭口姿态。
(2)在闭口姿态下,Cx、Cz的脉动值为46.4%,Cy的脉动值在145%左右,其原因是列车顶部区域的流场涡结构复杂化使Cy振荡周期的规律性增强;开口姿态下,Cy的波动降低为闭口工况的30.2%,可以得出受电弓在纵向的振动较为强烈,同时气动力系数对应的频率范围明显大于闭口姿态运行的工况,可见横风对开口姿态运行时绕流场特性的作用更加显著。
(3)在闭口姿态运行工况,My的频谱比Mx和Mz的要宽,说明在横风作用与受电弓自身频率耦合的范围更宽,危险性更大。开口姿态运行时Mx最大值和平均值均大于闭口姿态工况,My完成一个周期变化所需时程小于闭口姿态的工况,开口姿态下气动力矩系数的频域宽度大于闭口姿态运行的工况。
