物流基础设施的网络效应促进我国区域经济增长实证研究

邹德明 博士生

（中国人民大学商学院 北京 100872）

引言与文献综述

21世纪至今，我国经济增长明显处在投资驱动阶段，基础设施投资对宏观经济增长起到重要的促进作用，而物流基础设施则是基础设施中最重要的一个组成部分。物流基础设施是指在供应链的整体服务功能上和供应链的某些环节上，满足物流组织与管理需要的、具有综合或单一功能的场所或组织的统称，主要包括公路、铁路、港口、机场流通中心、仓储、运载设施以及网络通信基础等，本文主要考察主要交通运输层面上的物流基础设施。在学术界，基础设施促进经济增长已经得到了大量理论分析和实证检验（谭清美、冯凌云和葛云，2003；周君，2006），但是基础设施通过哪些机制来促进经济增长，各类机制的影响程度又如何，这一问题尚未形成一个统一的分析框架。因此，其内在的作用机制是后续值得进一步研究的课题。

大多数基础设施的一个重要特征是具有空间网络性，而投资决策主体之间的决策协调程度在一定程度上会影响基础设施的空间效应强度，比如在何地建设或何时建设。近年来，有学者开始关注中国物流基础设施的跨区域溢出效应（张学良，2012；刘生龙、郑世林，2013；李涵、唐丽淼，2015）。实证结果表明，基础设施的溢出效应非常显著，若不考虑空间溢出效应，会高估物流基础设施对区域经济增长的作用。除溢出效应外，地区之间通过统筹协调进行的投资决策所产生的网络效应也同样不容忽视。在缺乏区域间统筹协调的情况下，公共基础设施的投资规模很难达到合理的最优投资水平。由于基础设施投资可能会改变区域间经济活动的分布，因此有学者提出的模型中强调了在相邻竞争区域中拥有过多基础设施的风险（Romp& de Haan，2005），不协调的投资决策甚至还可能会对邻近地区产生负面的外部影响。同时，如果目标是要在包含所有区域的宏观层面上最大化总体福利水平，而不是针对某个单个地区时，基础设施的投资决策往往需要进行统筹安排（Schiff & Winters，2002）。然而，由于缺乏可观测数据以及适当的计量模型，聚焦于基础设施网络效应的实证研究始终较少。因此，相比于以往文献，本文研究意义在于丰富物流基础设施的网络效应的实证研究。

理论模型

本文借鉴Giacinto V D，Micucci G & Montanaro P（2012）提出的理论模型对基础设施的网络效应和非网络效应进行区分，并假设当两个地区之间以统筹协调的方式进行基础设施投资决策时，才将网络效应发挥到最大。在进行投资决策前，地区之间探讨了彼此合作的可能性，以便在众多投资方案中选择具有最高共有效用的一个，比如在道路基础设施投资中，可以以促进两个地区之间的物流整合性为目标共同扩张各自的区域网络。在此情况下，两个地区现在都可以获得更高的总体收益，包括自行投资所获得的收益之和W，加上溢出效应X，再加上额外收益P，即网络效应（统筹协调后的额外净收益）。

由于统筹协调投资代表着所有区域参与者的共同行动，因此可以将各个地区资本支出之间的相关性视为存在某种协调机制的依据。需要注意的是，尽管统筹协调行为确实是各个区域投资规模同步变化的可能原因之一，但其它因素也可以同样用来解释这种情况。

首先，考虑可观测的区域基础设施投资额的一种构成形式：

其中，i和t下标分别为区域和时期标识，Kt代表物流基础设施资本存量，则△Kti，t代表当期的物流基础设施资本增量，CCi，t和ICi，t变量分别代表区域间共有投资成分和区域个体特有投资成分，且不同区域间的CC具有相关性、各个区域间的IC不相关且与同一区域的CC正交。

接下来，区域间共有投资成分CC可以进一步分解为内生成分CCend和外生成分CCexog。CCend代表了某个区域基础设施投资水平对国家或者全球层面宏观经济发展的反应，而CCexog则代表不受宏观层面影响的区域基础设施投资水平，是受宏观经济以外因素影响但在区域间具有高度相关性的基础设施投资支出。

作为可能在区域之间引起同步决策反应的常见因素，可以考虑汇率波动、利率或商品价格变化的情况。在这些因素发生变化时，所有地区的GDP和税收水平都将同步受到影响，但是严格外生的共同政策行为之间的联动也可能是由统筹协调之外的因素引起的。为了考虑到此问题，我们引入了进一步的分解：

CCcoordi，t代表经过统筹协调决策的资本支出，它是外源性区域资本支出，t的一部分，则代表可能存在的伪联动因素，它与正交。伪联动的一个重要可能性是来自于政治经济周期效应（Nordhaus，1975）。

在计量分析过程中，可以通过以下两个简单方程式总结以上分析方法：

上述第一个等式为政策反应函数，将公共资本支出的内生响应与向量ζ中包含的随机变量的滞后值相关联，并假定该向量包含影响i地区的所有常见宏观经济扰动相关信息。为了便于分析，假定使用线性函数形式。一旦识别了CCend和CCspur，CC中的统筹协调决策成分CCcoord便也可被识别出来。

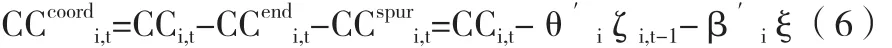
上述公式表明，对CCcoord进行分析的前提，是首先需要对共有效应CC进行样本估计。

计量模型

计量过程中将结合使用共有相关效应面板模型和结构VAR模型，对物流基础设施投资网络效应的经济影响进行实证分析。首先是利用共有相关效应面板模型将资本存量中的共有相关成分提取出来，接下来将提取出的成分引入VAR模型进行脉冲响应和方差分解分析。

本文采用Pesaran（2006）提出的CCE估计方法（Common Correlated Effects Estimate）对不可观测的共有相关成分进行估计，CCE估计的核心在于使用解释变量和被解释变量截面均值代表变量之间的不可观测因素。

图1 各省份1997-2017年物流基础设施资本存量

图2 物流基础设施资本存量的共有相关效应成分

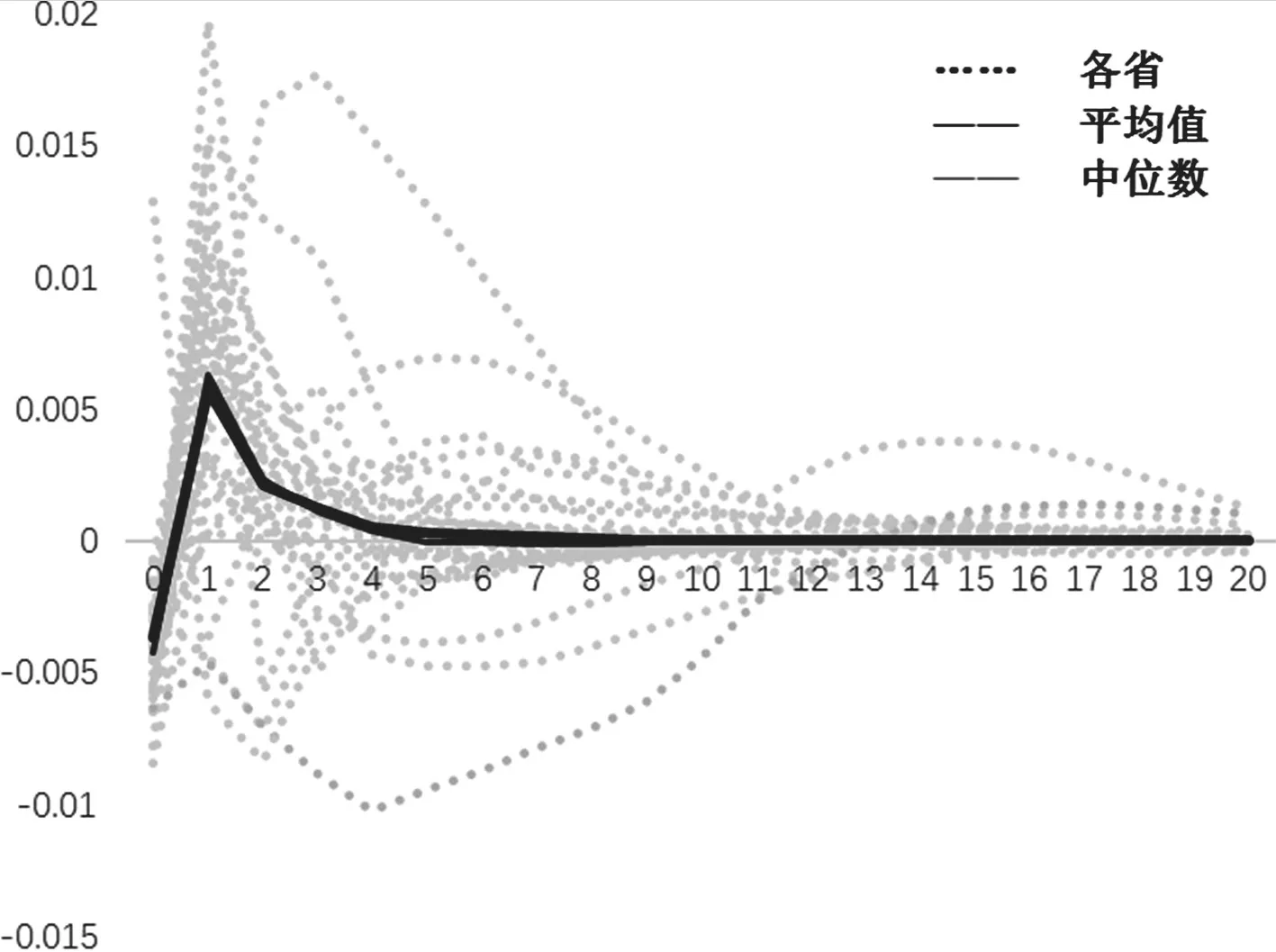
图3 脉冲响应函数（物流基础设施资本增长率-统筹协调的网络效应成分）

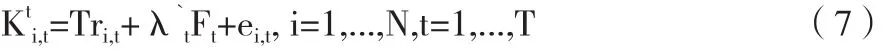
其中：Tri，t是给定区域特有的决定性趋势项；Ft是r×1的共有相关因子向量（r＜N）；λi是因子负荷向量；ei，t是残差项，在各个区域之间可能存在弱相关；假定共有相关效应因子之间正交，Ft与ei，t之间正交。用估计项序列的共有相关成分，并假定其解释了不同区域之间的共同运动。它的序列差分就等于前文中的共有效应投资CC。

一旦获取了对地区公共资本存量的共有相关成分的一致估计，基于前文理论模型的计量实践将采用结构VAR方法，以评估基础设施资本支出的宏观经济影响（Pereira，2000；Kamps，2005）。通常VAR系统会涉及三个内生变量即GDP（Y）、资本存量（K）和人力资本存量（L），同时这些变量之间允许存在协整关系。假定滞后阶数为ρ＞0，i地区的VAR模型中的三个等式可以表示为：

其 中，Xi，t=[Ki，t，Li，t，Yi，t] ′，εi，t是 协 方 差 矩 阵E(εi，tε′

i，t)=Ωi的白噪声过程，Di，t则为一系列决定性变量，可能包括常数项和趋势项。由于各个时间序列变量不平稳，因此对其均取对数后做差分处理，上式变为：

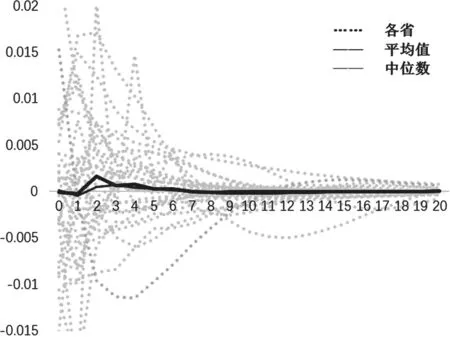
图4 脉冲响应函数（物流基础设施资本增长率-个体特有的非网络效应成分）

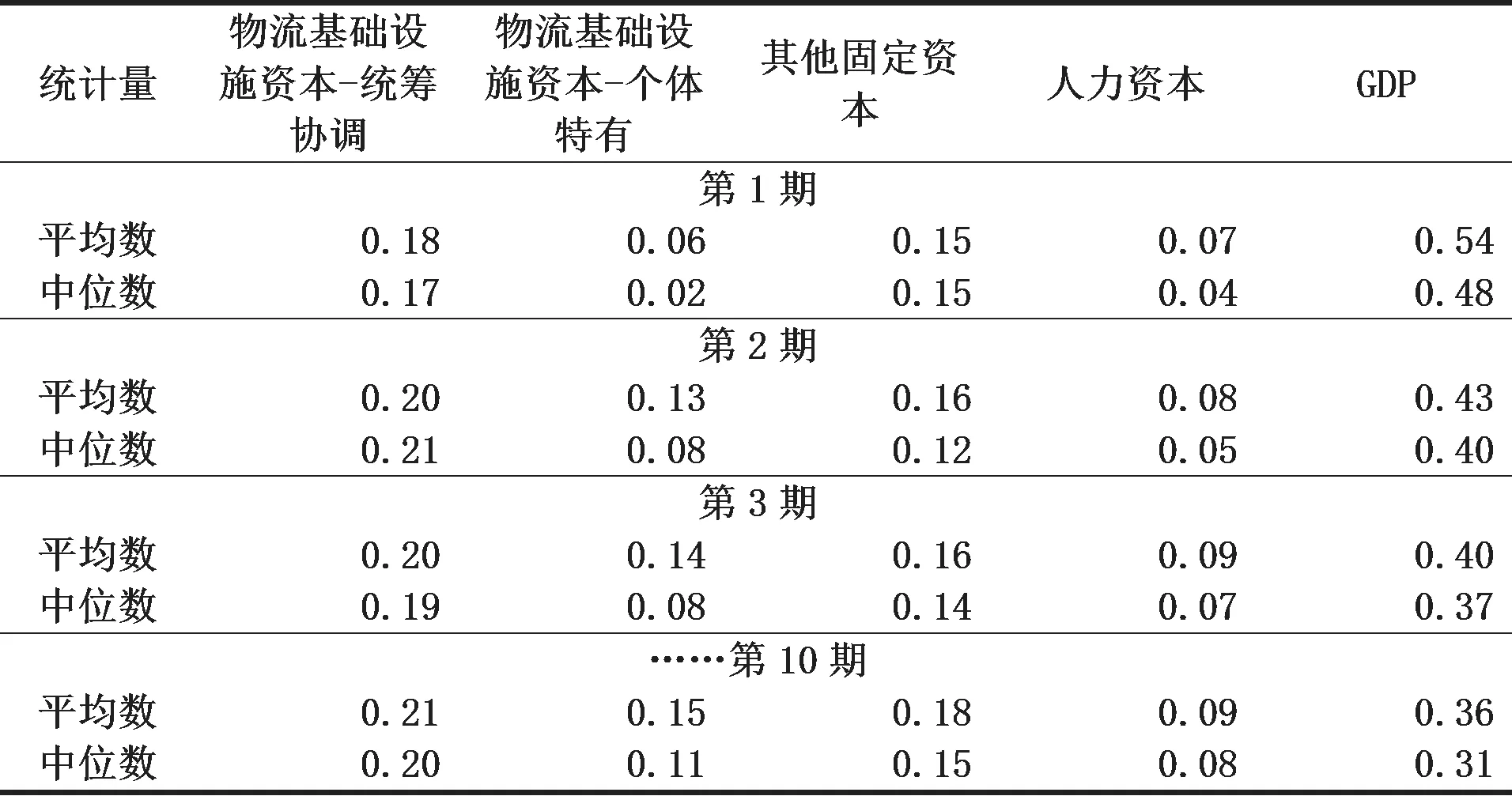
表1 方差分解

由于取对数且做差分处理，变量的计量经济含义由存量变为增长率。为了分别估计统筹协调效应冲击和个体特有效应冲击，继续将上述计量模型变为：

由于误差协方差Σi不是对角线矩阵，因此无法对该模型中的随机冲击进行任何结构性解释。在VAR模型的相关文献中，通常采用的方法是利用Choleski分解来确定结构性冲击顺序，并假设Kt变量的排序优先级最高（Pereira，2001；Kamps，2005）。同时，Choleski分解也使得我们可以分别对物流基础设施资本的统筹协调效应冲击影响和个体特有效应冲击影响进行估计。在递归假设下，将结构扰动与误差协方差矩阵联系起来的解析关系集，可以由以下线性方程的下三角矩阵系统给出：

第一个结构性扰动项eΔlnK～ti，t代表物流基础设施资本中共有相关效应成分的不可观测残差；与此同时，通过上述构造，它与系统中内生变量的滞后值集合相正交。因此，结构冲击 eΔlnK～ti，t可以看作是基于结构VAR模型对统筹协调效应CCcoord冲击的有效估计。

数据来源

计量模型采用了1997-2017年中国31个省份的面板数据进行分析，数据来源主要于《中国统计年鉴》和《中国劳动统计年鉴》。

GDP数据来源于《中国统计年鉴》。以1996年为基期，使用GDP指数对名义GDP进行调整，得到各省各年实际GDP。

劳动力投入数据来源于《中国劳动力年鉴》。用人力资本存量来反映各省的劳动力投入情况，常用的人力资本存量计算方式包括成本法、收益法和教育水平法。考虑到数据可得性，本文借鉴徐曌（2017）的做法，使用教育水平法测算各省人力资本存量。

资本存量数据则参照过往文献，使用永续存盘法来测算各省固定资本存量。这一测算方式涉及到基期资本存量的计算、固定资产投资价格指数的设定、资产经济折旧率等具体问题。本文按照张军（2004）采用的方法，对各省份不同时期的资本存量进行估计。

至此，可以得到1997-2017年期间我国31个省份的平衡面板数据，N=31，T=21。在所有的变量中，我们首先关心的是物流基础设施资本存量，图 1展示了1997-2017年期间31个省份的物流基础设施资本存量情况。

实证分析

按照前文所述，实证分析将分为两阶段进行。第一阶段是利用共有相关效应模型，将面板数据中的共有相关成分提取出来；第二阶段是利用提取出的共有相关成分作为输入，建立结构VAR模型对统筹协调成分的经济影响进行分析。

为了实施共有相关效应面板模型方法，首先要对模型结构进行设定。考虑到物流基础设施存量序列在样本期内显示出明显的上升趋势，因此设定一个既包含常数又包含趋势的因子模型，提取出的共有相关效应成分如图2所示。

通过第一步得到共有相关效应成分的估计值后，开始进入实证的第二阶段，即结构VAR模型估计。除了两个物流基础设施资本序列（总体水平及其共同相关效应组成部分）外，还包括以下变量：按不变价格计算的地区GDP水平、除物流基础设施外的固定资本存量以及人力资本投入。所有变量都以对数形式引入，但即便以对数形式引入，Dickey-Fuller单位根检验结果显示面板数据中大多数仍是非平稳序列。按照常规分析思路，接下来应当查看序列间是否存在协整关系，但是由于无法保证31个截面均同时存在协整或者不存在协整，进而无法保证估计方法的一致性，因此本文统一对所有序列进一步做差分处理，对应的经济含义变为增长率。差分后，所有省份VAR模型均通过了稳定性检验，可以进行脉冲响应和方差分解分析。

此外，根据标准信息标准提供的参考来选择模型的最优滞后期。除少数例外，多数截面滞后期为1。最后，为了控制常见的政治经济周期影响，在结构VAR模型中加入一组外生虚拟变量，代表是否处在重要换届选举时期。虽然脉冲响应结果在各个区域之间显示出相当大的异质性，但整体趋势却非常明显。如图 3、图 4所示，当我们考虑各个省份脉冲响应的平均值或中位数时，除当期外，物流基础设施资本对区域GDP长期响应是正向的。

考虑到模型中变量的经济含义已转换为增长率，因此物流基础设施资本存量增长率的冲击并不会对GDP增长率产生较为长远的影响。脉冲响应结果表明，不论统筹协调成分冲击还是个体特有成分冲击，到第10期都已经接近消退。不同的是，正如经济学理论所强调的网络外部性的重要性，预计统筹协调形成的网络效应的冲击影响要更大。以各省份脉冲响应的平均数进行评估，在采取统筹协调决策进行物流基础设施投资的情况下，GDP增长率对其一个标准差冲击的响应在第一期达到峰值，约等于0.57%（P+W+X），而对个体决策投资冲击的响应则在第二期达到峰值，约等于0.16%（W），前者几乎是后者的4倍。从0-20期累计影响看，前者是0.75%，后者则为0.21%。

在评估了脉冲响应系数的符号方向和相对幅度之后，方差分解结果进一步提供了有关短期和长期内统筹协调成分和个体特有成分冲击分别对区域GDP动态贡献的更多信息，如表1所示。再次观察31个省份方差分解结果的平均数，物流基础设施统筹协调成分的冲击对GDP增长率的贡献是巨大的，长期来看，GDP增长率变化的约五分之一可归因于统筹协调成分的结构性干扰。

研究结论

在探讨关于物流基础设施对我国区域经济影响的过往文献中，虽然很多都强调了物流基础设施的网络效应，但是很少有文献对网络效应的经济影响程度进行分析，而这正是本文研究的侧重点。本文首先构建起一套理论模型，强调通过区域间统筹协调决策的投资行为，可以有效增强公共基础设施投资的正向网络效应，而不协调的决策则可能在包含所有区域在内的整体层面上产生较低的福利收益，甚至可能导致负面的溢出效应。

从这一背景出发，在探讨物流基础设施投资对外部区域的影响时，本文并未采用区分地区内部和外部资本积累的常规做法，而是对统筹协调和个体特有投资决策进行区分，进而评估与宏观经济演进无关的物流基础设施投资决策对区域GDP的影响。由于缺乏数据支持，我们无法直接观测到投资决策是属于统筹协调还是个体特有类型，因此本文尝试利用共有相关效应面板模型，从可观察到的区域物流基础设施资本存量中，间接识别出区域间共有相关的资本存量成分，这一部分存量中包含了统筹协调投资决策的影响。接下来，将识别出的共有相关成分作为一个新的变量引入到结构VAR模型中，评估统筹协调投资决策形成的物流基础设施资本增长对区域经济增长的影响。

实证结论主要包括：一是物流基础设施确实对宏观经济产生了较大的正向影响；二是这一正向影响主要归因于统筹协调投资决策所产生的网络效应和溢出效应，经过统筹协调的物流基础设施投资对区域GDP的影响程度平均是个体特有投资决策的3-4倍；三是在1997-2017年期间，我国各省份之间统筹协调进行物流基础设施投资的决策机制在逐渐强化，这可能暗示着我国中央政府在大型基础设施投资过程中起到的协调作用和集中决策作用正在变得越发重要。