基于EMD-Hilbert的行星齿轮箱在线故障诊断

崔慧娟

(咸阳职业技术学院机电(技师)学院，陕西 咸阳 712000)

随着风电技术的快速发展，行星齿轮在大型风力发电机组中发挥着越来越大的作用。而风电设备经常处在恶劣环境中，常年经受较大的风向载荷，导致其内部行星齿轮传动系统受到严重磨损，这样会造成整个风电机组严重损伤，甚至会导致风力发电系统直接瘫痪[1-4]。因此，对风电机组行星齿轮箱磨损状态进行故障诊断检测具有重要的意义。

近些年，国内外很多专家和学者对行星齿轮箱故障诊断做了大量研究，主要是针对行星齿轮在传动过程中的磨损状态进行故障诊断，从而为风电机组行星齿轮箱故障提供预警。其中：安学利等[5]采用ITD(intrinsic time-scale decomposition,固有时间尺度分解)和LS-SVM(least squares support vector machines，最小二乘支持向量机)方法对风电机组齿轮磨损信号进行分解和识别，能够有效识别故障; 赵洪山等[6]通过统计过程控制的方法对齿轮箱磨损出现的故障进行监测，并根据样本所出现的概率判断齿轮磨损故障程度；陈法法等[7]利用局部切空间排列与MSVM(multivariate support vector machine)对齿轮磨损故障状态进行了诊断，实验结果证明该方法是可行的。由于行星齿轮箱传动系统是一个高速、非线性运动系统，采集的齿轮箱磨损信号在分解后容易产生虚假信号，常规的SVM(support vector machine)识别算法容易误判齿轮磨损状态，因此针对这种传动不平稳的信号，借用Hilbert调制技术来解决。

本文为了解决上述问题，提出了一种基于经验模态分解(EMD)和Hilbert解调技术(HT)的风电机组行星齿轮箱齿轮磨损在线故障诊断方法。鉴于Hilbert技术对信号进行变换之前，需要将信号分解成一系列不同尺度波动或趋势的本征模态函数(IMF)，本文结合经验模态分解算法，可将非平稳信号分解为模态函数分量(IMF)和残余量并去除无用的残余量，从而满足Hilbert变换的条件；然后对分解得到的IMF分量求取峭度和峰值并进行归一化处理，对这些包含故障信息的IMF分量进行信号重组和谱分析，选取重组信号中带宽为实际故障信号特征频率的1～3倍的故障特征频率，对该信号进行带通滤波并运用Hilbert解调方法，根据解调出来的频率成分来实现故障诊断，最终达到风电机组行星齿轮在线故障诊断的目的。

1 模态分解理论

经验模态分解(empirical mode decomposition，EMD)算法由美国学者Huang博士在1998年首次提出，是为解决Hilbert变换的条件限制而提出的一种方法[8-9]。该方法是将非平稳信号分解为模态函数分量(IMF)和残余量并去除无用的残余量，使其满足Hilbert的两个基本条件，然后利用EMD方法将信号分解成一系列具有不同尺度波动或趋势的本征模态函数(IMF)，进一步进行Hilbert变换，从而获得信号的时频谱[10-11]。

信号序列x(t)的EMD算法分解具体流程如下[12]：

1)寻找信号序列x(t)中的极大值点与极小值点，然后采用三次样条曲线进行上下包络拟合，记录上下包络线为a(t)和b(t)，并求解其均值序列μ(t)。

μ(t)=(a(t)+b(t))/2

(1)

2)从采集的原始齿轮信号序列x(t)减去上下包络均值μ(t)，得到余值曲线H(t)。

H(t)=x(t)-μ(t)

(2)

3)对步骤2)获取的余值H(t)进行相关判别，如果满足Hilbert变换的IMF和残余量两个条件，将余值H(t)作为x(t)信号的一阶本征模式分量c(t)；若不满足，将余值H(t)信号作为新的分量，反复执行步骤1)、2)，直到满足Hilbert变换的IMF和残余量两个条件。

4)将c(t)从原始信号x(t)中分离出来，得到残余项p(t)，判断残余项能否继续分解，若能则将p(t)作为新的信号重复以上步骤，若不能则循环结束。

最终，信号x(t)被EMD分解后得到信号x(t)的若干个IMF分量ci(t)和残余量pi(t)：

(3)

2 Hilbert变换理论

Hilbert变换理论对于本文风电机组行星齿轮磨损故障在线诊断具有重要意义，是信号分析的有利工具。Hilbert变换理论是由德国科学家Hilbert提出来的，其简单定义为：

(4)

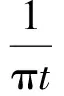
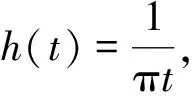
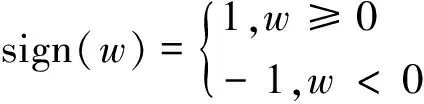
(5)

因此，由分析可知Hilbert变换[14-15]相当于幅频特性等于1的全通滤波器，其特性如图1所示。

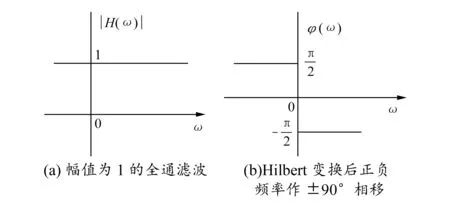
图1 Hilbert变换(全通滤波器)特性

Hilbert包络解调就是对含有调制信息的原始信号x(t)求希尔伯特变换，从而得到x(t)的虚部g(t)，然后由原始信号x(t)及虚部g(t)组成解析信号，并得到x(t)的包络信号，随后对其求频谱[16-17]，进而获得x(t)的包络解调谱。

假设齿轮啮合振动的载波信号X(t)为：

X(t)=Bsin(2πfzt+θ)

(6)

式中：fz为啮合频率；θ为初相位；B为载波信号幅值。

故障齿轮调制信号xg为：

xg(t)=1+mcos(2πfgt)

(7)

式中：fg为故障特征频率；m为调制后信号幅值；t为时间。

设齿轮的载波信号为：

x(t)=Bm[1+mcos(2πfgt)]sin(2πfzt+θ)

(8)

式中：Bm为振动信号幅值。

Hilbert变换就是为了能够把幅值调制信号Bm[1+mcos(2πfgt)]分离出来。因此，x(t)的Hilbert变换h(t)为：

h(t)=Bm[1+mcos(2πfgt)]cos(2πfzt+θ)

(9)

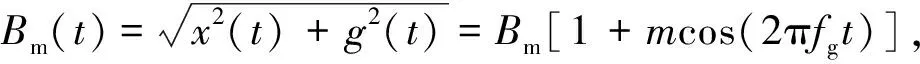
定义x(t)的解析信号J(t)为：

J(t)=x(t)+jh(t)

(10)

3 行星齿轮磨损在线故障诊断模型构建

3.1 在线故障诊断流程分析

风电机组行星齿轮箱齿轮磨损信号在线故障诊断流程如下：

1)利用信号传感器对不同磨损状态下的风电机组齿轮进行信号采集，在将信号进行阈值降噪预处理后使用EMD方法进行分解,并计算IMF模态分量函数；

2)以峭度和峰值作为衡量指标，计算并求解IMF函数中两个指标的信号值，对信号进行相关性重组，求解出重组后信号的幅值谱；

3)对实际故障齿轮信号进行带通滤波，计算故障特征频率，选取风电机组齿轮箱故障特征频率参数；

4)选取采样信号中带宽为实际故障信号特征频率1～3倍的信号作为故障特征信号，对该信号进行带通滤波并根据运用Hilbert解调方法解调出来的频率成分实现故障诊断。在线故障诊断流程如图2所示。

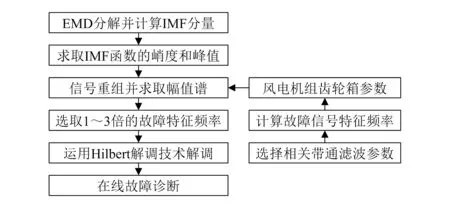
图2 行星齿轮箱齿轮磨损在线故障诊断流程图

3.2 行星齿轮箱试验平台及实验分析

1)信号采集及降噪预处理。

如图3所示，本文采用常规行星齿轮箱齿轮传动系统代替风电机组行星齿轮箱来进行故障信号测试。实验采集信号的频率为10 358 Hz，采样时间为20 s，齿轮箱主轴转速为20 r/min。根据各级齿轮相关参数(表1)，计算20 r/min转速下每一级的啮合频率和转频，进而计算得到20 r/min转速下每一级的行星轮齿轮的分布式故障特征频率为326.3 Hz。

图3 行星齿轮故障诊断实验平台图

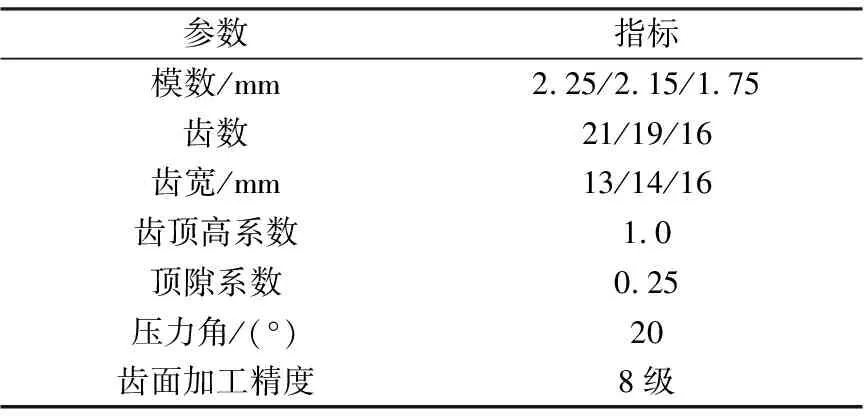
表1 行星齿轮箱相关参数

为了提前对行星齿轮箱齿轮磨损故障发出警告，实验采集齿轮初步开始磨损的故障信号，目的是为了检测齿轮开始出现磨损故障的状态。降噪处理后的行星齿轮箱传动时/频域信号如图4所示。

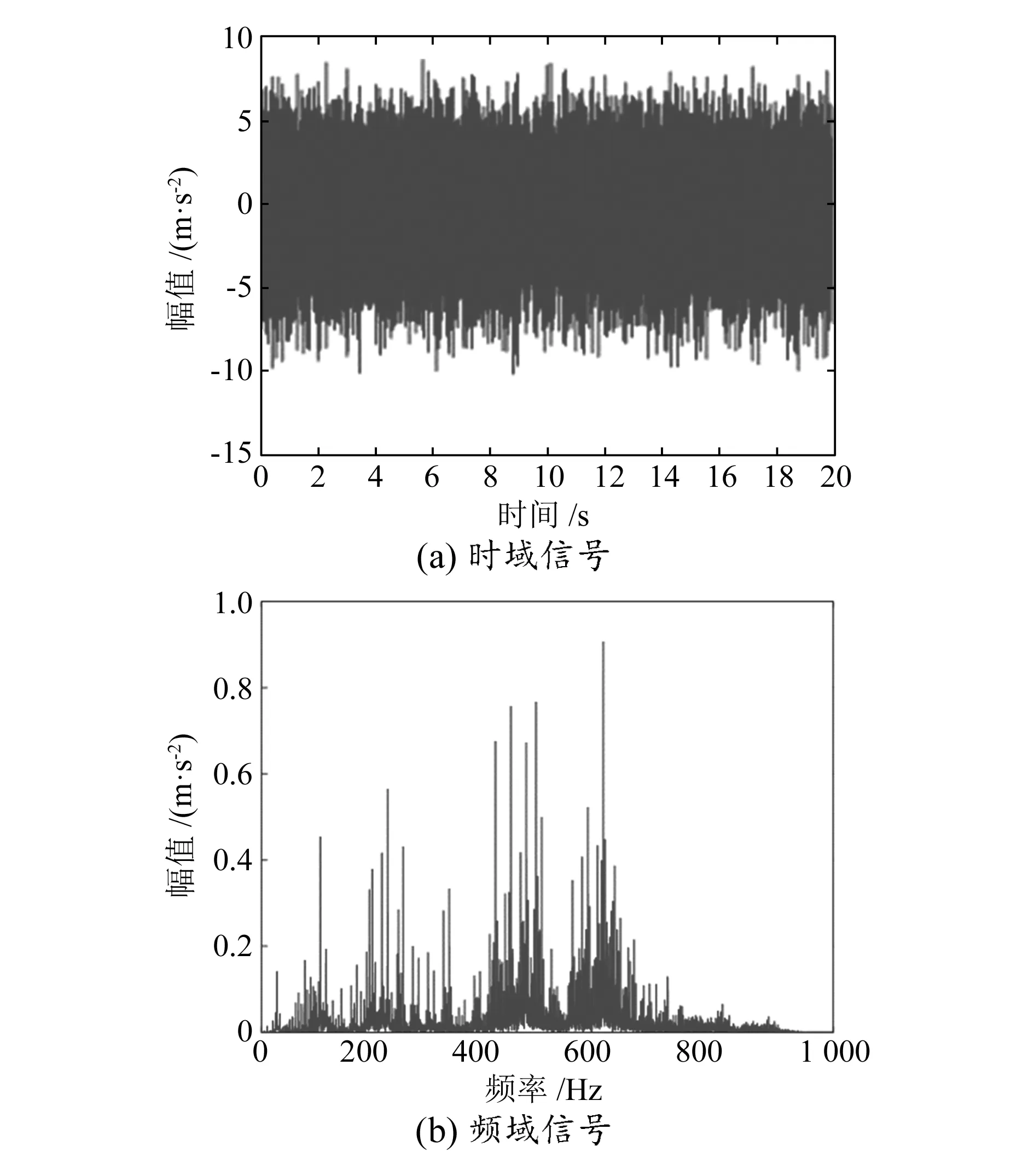
图4 行星齿轮箱齿轮磨损故障降噪后时/频域信号

2)EMD分解。

对图4预处理后的信号进行EMD分解，计算分解后信号的相关系数并且获取IMF1～IMF10分量图。信号EMD分解后的各阶IMF分量如图5所示。

图5 行星齿轮磨损信号EMD分解的IMF1～IMF10时域图

图中IMF1～IMF10为前十阶模态函数，U为残余分量。对各个IMF分量进行峰值和峭度分析，并以所有分量中每个指标的最大值来对相应的指标进行归一化处理，其值越接近1，表明其在各个分量中的值也越大，如图6所示。

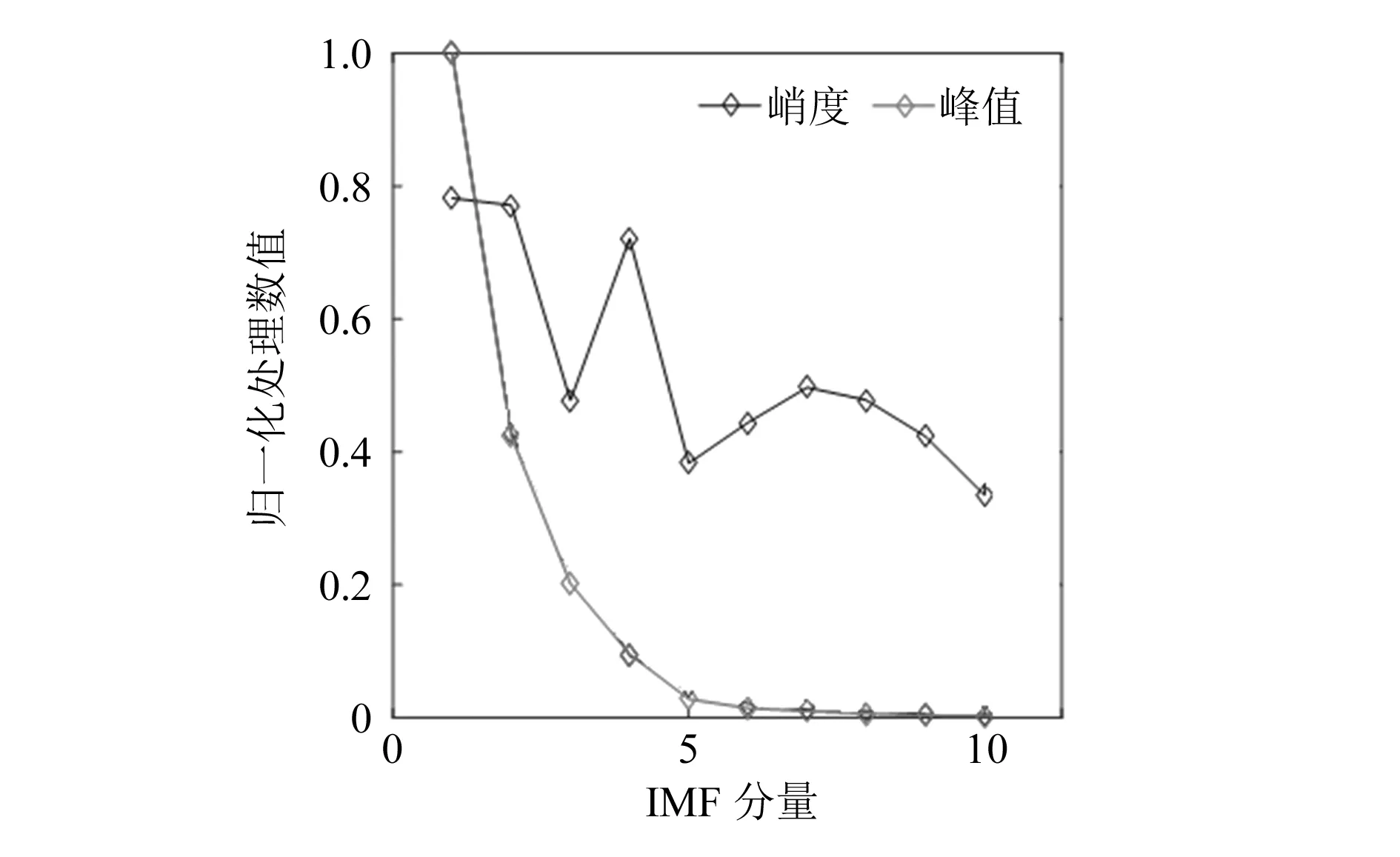
图6 行星齿轮磨损信号分解各IMF分量指标图

3)Hilbert变换技术。

由图6得知，IMF1～IMF4分量函数的峭度和峰值都比较大，其他分量函数变化波动较小，可以舍弃。综合分析后将IMF1、IMF2、IMF3和IMF4进行重组，并对重组后的齿轮故障信号求幅值谱，如图7(b)所示。行星齿轮正常状态下重组后的信号幅值谱如图7(a)所示。

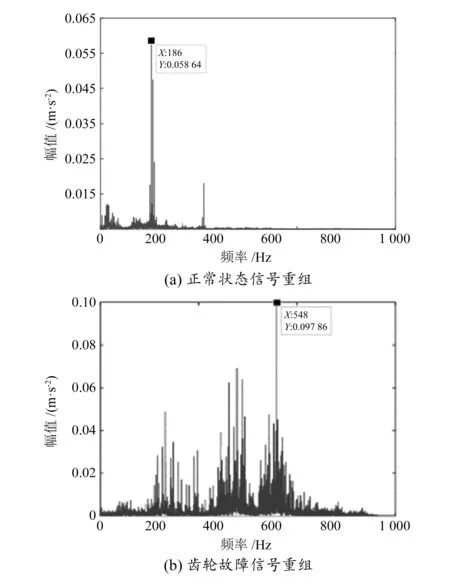
图7 行星齿轮正常/磨损重组信号幅值谱对比

4)信号的包络解调处理。

由于行星齿轮磨损故障的特征频率为326.3 Hz，因此以中心频率为186 Hz对正常状态下重组信号(图7(a))，以中心频率为548 Hz对行星齿轮故障状态下重组信号(图7(b))，分别进行带宽为800 Hz的带通滤波，然后进行Hilbert解调，获得的解调谱如图8所示。

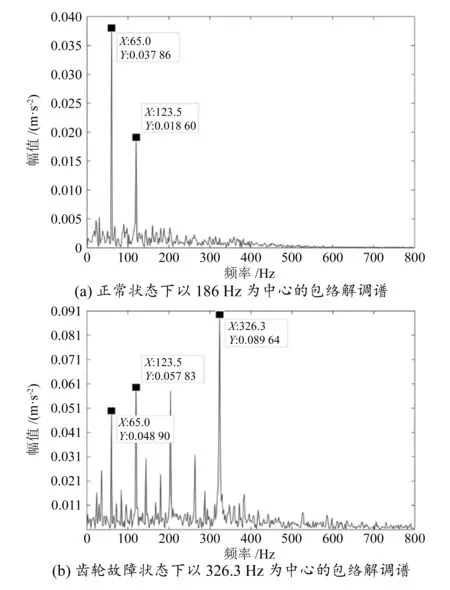
图8 行星齿轮各状态下重组信号包络解调谱

由图8(a)可以看到，由正常状态下以186 Hz为中心的信号被转频调制；由图8(b)能够看到，在频率为65 Hz时，齿轮幅值为0.048 90 m/s2，与正常状态下的幅值0.037 86相差较小，说明齿轮还处于正常状态下；在频率为123.5 Hz时，齿轮幅值为0.057 83 m/s2，相比正常状态，幅值开始增大，说明齿轮已处于磨损状态下；当频率为326.3 Hz时，幅值为0.089 64 m/s2，相比正常状态，幅值较大，且幅值所对应的频率正好与行星齿轮完全故障特征频率相等，说明行星齿轮完全处于故障状态。

由此可知，本文理论分析计算结果和实验结果数据基本保持一致，验证了本文提出的一种基于经验模态分解(EMD)、Hilbert解调技术(HT)的风电机组行星齿轮箱齿轮磨损在线故障诊断方法的可靠性。

4 结束语

本文提出的基于EMD分解和Hilbert解调技术的齿轮故障诊断方法，以EMD分解为信号分解方法，获取非平稳信号模态函数分量(IMF)和残余量，实现了故障信号分解；然后采用Hilbert解调技术对正常状态、齿轮故障信号获取包络解调谱。将两种方法相结合，并运用在实际试验中，结果表明，将EMD分解和Hilbert解调技术应用在状态识别和故障诊断中是可行的。