新型投球滑套式可变径球座的研究与设计

杜永军，胡 卫，宋树林，王印发，王 薇

(1.东北石油大学机械科学与工程学院，黑龙江 大庆 163318) (2.吉林油田扶余采油厂，吉林 松原 131200) (3.大庆钻探钻井四公司，黑龙江 大庆 163318) (4.宝鸡石油机械有限责任公司，陕西 宝鸡 721000)

压裂就是利用水力作业使油气层形成裂缝的一种方法，其中采用投球滑套作业方式的多层压裂技术以其独特优势在国内各大油田被广泛使用，但其一趟管柱的可压裂层数因受压裂球尺寸的限制而受到严重制约，导致可压裂层数极其有限。在多种情况下，一趟管柱不能解决更多级压裂的情况，且会增加压裂施工成本。同时传统的投球滑套作业方式中投球尺寸必须从小到大投放，否则会出现漏层现象，导致压裂事故，造成严重经济损失[1]。

为了解决这个问题，笔者采用可变径球座替代原有的固定球座，设计了一种新型的投球滑套式压裂工具，达到了采用同一尺寸小球完成多层压裂的目的，在理论上解决了如何提高投球滑套式压裂作业一趟管柱的最大压裂层数和投球顺序严苛的问题。针对这种替代方式，笔者根据其工作原理，建立了相应的简化物理模型以及力学模型，并通过ANSYS软件对这一结构模型进行了建模和受力分析，研究变径过程中应力的变化情况。

1 可变径球座的工作原理

传统的投球滑套作业方式是利用油管柱将压裂工具下放到预定的压裂部位，然后加压完成坐封，随后继续加压，并通过投球准确地控制地层开始压裂的位置，但压裂球必须按从小到大的顺序依次投放到压裂管柱中[2]。当采用可变径球座代替原有的固定球座后，压裂球可选用同一直径的小球，如要控制某一层进行压裂时，只需要控制这一层的可变径球座的直径变小(球座截面形状最开始为C型，直径减小后变为O型,且可变径球座变为O型后的径向尺寸<压裂小球的直径尺寸<可变径球座为C型时的径向尺寸)，再通过投入压裂球打开相应的压裂滑套，即可完成相应地层的压裂工作，可变径球座工作原理如图1所示。

2 可变径球座的计算模型

为了确保球座在变径过程中的安全性与可靠性，根据其工作原理以及设计出来的球座尺寸建立计算模型，并求解得到应力云图，以便对球座进行强度校验。

2.1 物理模型

取在套管外径为139.7 mm的油井中工作的压裂工具为研究背景，为了简化计算，建立模型时只选取可变径球座和压裂滑套底部作为研究对象，并根据各个部分的功能特点，将压裂滑套底部简化成一个含有内锥面的圆柱体，最终得到此物理模型的二维简图(如图2所示)以及尺寸(见表1)。

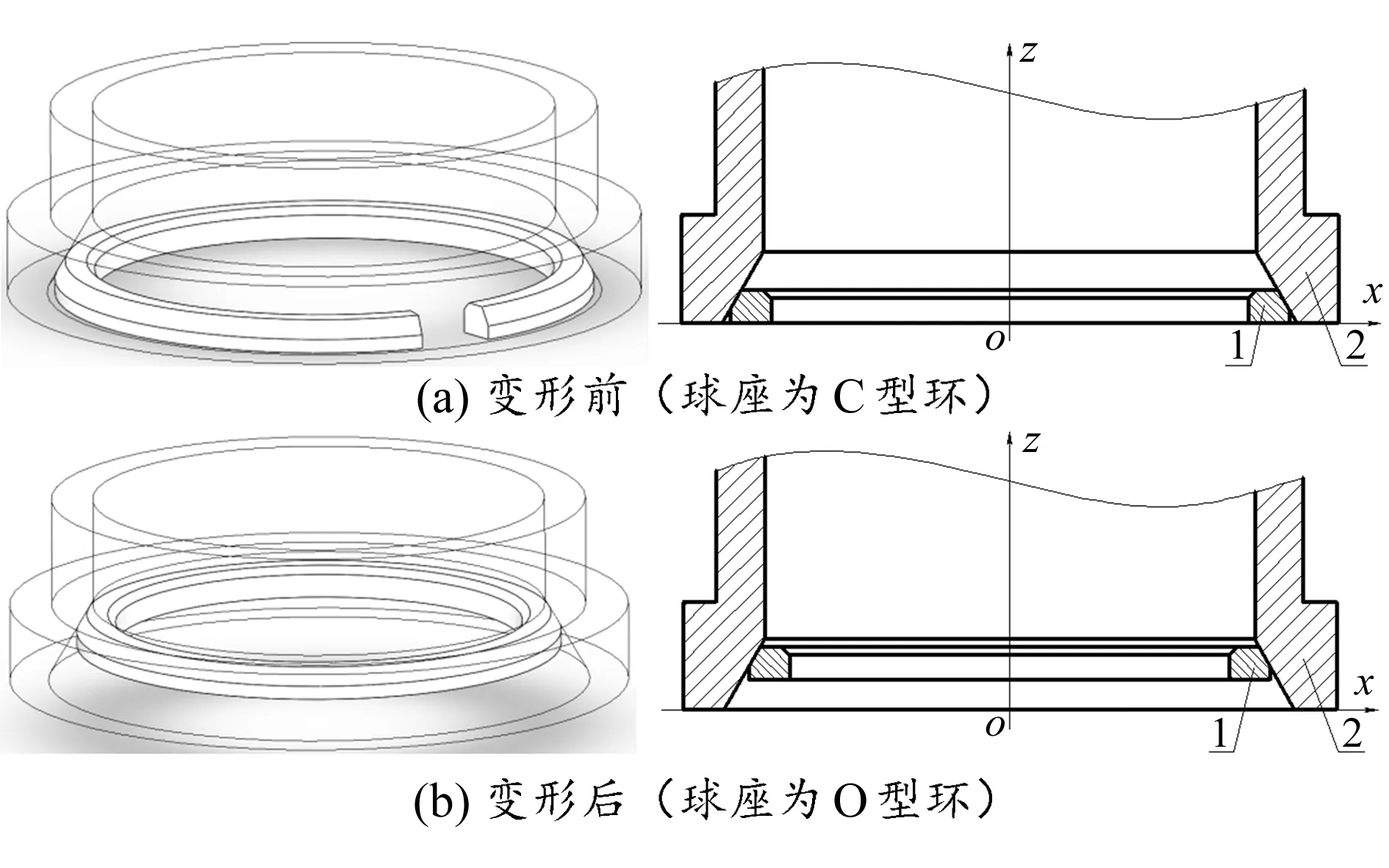
1—可变径球座;2—压裂滑套

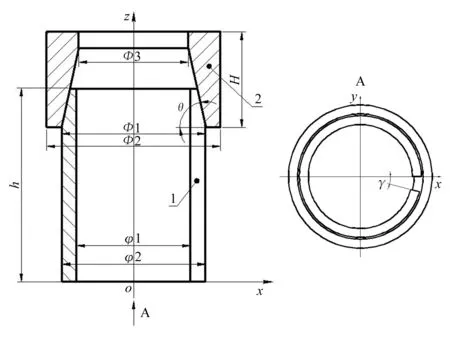
1—可变径球座;2—压裂滑套尾部

表1 模型尺寸参数表

注：1)图中所示的压裂滑套底端并非其实际结构形状，模型为了方便计算将压裂滑套底端进行了简化处理，并只截取了其对可变径球座产生影响的部分来分析；2)表中可变径球座尺寸值的设计是按照当其发生轴向(z向)位移10.0 mm时，在压裂滑套底部内锥面的作用下,可变径球座刚好闭合成O型，且变形后内圈直径φ1为28.0 mm来确定的。

2.2 力学模型

通过观察分析可以发现，此可变径球座属于反射对称模型，因此为了更好地建立力学模型，这里采用柱面坐标系[3]。规定柱面坐标系中的z轴与图2中物理模型的z轴重合，柱面坐标系中的r,θ所在平面与图2中物理模型的x,y所在平面重合，且θ环向起点与x轴正方向重合。在可变径球座工作过程中，其形状的改变可以看作是由其位移所引起的，因此在建立力学模型时，主要采用位移分量来表示，得到如下几何方程：

式中：εr,εθ,εz与γrθ,γrz,γzθ分别为可变径球座正应变与剪切应变分量；ur,uθ,w分别为可变径球座径向、环向以及轴向位移。

依据广义胡克定律,同时结合上述方程可得：

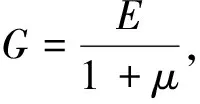
取可变径球座一微小单元(如图3所示)，根据∑Fr=0、∑Fθ=0、∑Fz=0可以建立相应的平衡微分方程。

如果采用位移分量来表示，则得出的平衡微分方程表达式太长，因此这里采用保留应力边界条件的形式，得到如下方程式：

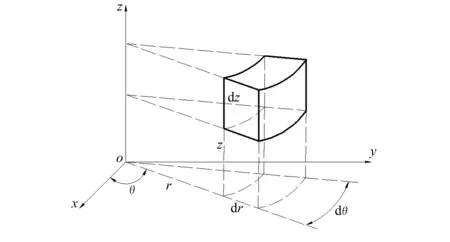
图3 微型单元图

式中：Kr,Z分别为可变径球座径向体力和轴向体力分量。

2.3 边界条件

由于可变径球座为一反射对称模型，因此其在工作过程中对称面上点的环向位移应为零，也即图2模型中与X轴正向夹角为(180°-γ/2)且在Y轴正半轴区域平面上的点的环向位移uθ|θ=180°-γ/2=0；可变径球座开口处两对应面上的点的环向位移uθ=γ/2；可变径球座所受的轴向体力分量Z=13.37 kN，径向体力Kr=0；在不考虑拉伸变形的情况下，可变径球座上点的最大理论轴向位移wmax=10 mm。同时，通过分析模型可以发现，模型中可变径球座的3个位移分量ur=f1(r,θ,z),uθ=f2(r,θ,z),w=f3(z)，且它们之间存在着一定的对应关系，只要其中一个位移分量确定，其他2个位移分量也会随之确定。

3 模型的求解及结果分析

上述力学模型方程式涉及的变量较多，人工求解不方便。这里笔者利用ANSYS软件的计算功能来对上述模型进行求解。通过计算，最终得到如图4所示的环向变形云图(求解得到可变径球座的最大轴向位移为10.26 mm)。

从图4中可以发现，可变径球座在变形的过程中遵循反射对称原则，最大变形出现在可变径球座开口两端处，最小变形出现在可变径球座对称面上，且其位移量关于对称面反射对称，这与上述边界条件完全符合。

图4 可变径球座环向变形云图

对于可变径球座变径的过程，在分析计算得到各个应力值之后，需要通过屈服准则来对模型进行检验校核，而在计算过程中屈服准则一般会选用von Mises准则，也即采用范式等效应力进行校核。通过分析计算，可以得到如图5所示的von Mises应力云图。

从图5可以发现，可变径球座在变形的过程中，其应力也一直呈现出反射对称的现象，这种现象是由其结构形状所决定的。通过对比可变径球座的5个应力云图可以发现，可变径球座上端(带锥角的一端)容易出现应力较大的现象，且都是首先出现在内圈上，并且应力随着可变径球座轴向位移的增加而增大，这是由于当可变径球座发生轴向位移时，因锥角的存在会导致可变径球座内圈出现压缩变形，外圈产生拉伸变形，而且变形量会随着轴向位移的增大而不断增大(球座变为O型之前)，各点的应力值也就会随之不断增大。对于处于可变径球座上端内圈处的结点而言，由于内圈上的曲率半径值相对最小、应力最集中，所以最容易在此处的结点上首先出现应力最大的现象，并且通过软件提取的应力值可知此处最大的应力值为850 MPa，在其制作材料(42CrMo)允许的应力范围内。同时，通过观察可以发现,当可变径球座上受到轴向力之后，可变径球座可以正确地发生变形(由原先的C型变为O型，且最终在球座上几乎没有留下缝隙)，但由于球座在工作的过程中存在一定的拉伸与压缩变形，导致可变径球座变为O型时的轴向位移与设计时的预设值(10 mm)之间存在一定的误差，但由于其误差值相对较小(0.26 mm)，在工程上是可以接受的，因此可以认为按照此轴向位移值来设计是可行的。

图5 可变径球座von Mises应力云图

在模型分析过程中，由于工程上一般只关心其危险截面、危险点的变化情况,因此为了进一步对模型进行研究，在分析过程中选取球座上容易出现较大von Mises应力的5个样点(即在可变径球座上端内圈处选取5个样点，由于应力也存在反射对称的现象，因此选取的样点位于对称面的同一侧，如图6中A～E点)为研究对象，可以得到结点von Mises应力与其z向位移w的关系图(如图7所示)和最大轴向位移时各点的应力与其发生的实际位移情况图(如图8所示)。

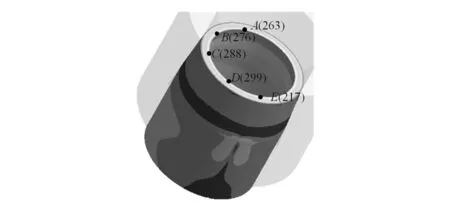
图6 A～E结点位置

从图8可以看出，这5个结点应力值处于同一数量级，相差不大，且随着位移值的增大而不断增大。通过对比5个结点在轴向上的最大位移值以及最大von Mises应力(如图8)可知，E点因处于可变径球座开口处，所以当可变径球座变为O型时，开口处两顶点间存在挤压现象，故E点处的应力值比其他4点处的大，又由于样点较少，样点间距离较大，且开口处的挤压现象对可变径球座影响的区域较小，因此导致图中5点间的应力存在突变现象。从图8中还可以发现，从A点到E点的最大轴向位移依次减小，这与可变径球座为C型结构有关，但因E点处位移值较其他4点处小，可能导致球与球座之间密封不严，高压液体对可变径球座的轴向力与其轴心不平行，存在一定的夹角，导致可变径球座整体受力不均，甚至在之后的压裂施工中因压力值的过大导致可变径球座出现异常变形，致使压裂失败。为避免上述现象，在可变径球座加工倒角时其倒角会有所偏斜(即倒角形成的锥面的轴心与可变径球座的轴心不重合,如图9中右图所示)，以保障球与球座之间形成正常密封，同时为了减小可变径球座开口处两顶点在闭合时的挤压应力，需进行磨边修角处理，最终得到可变径球座倒角情况如图9所示。

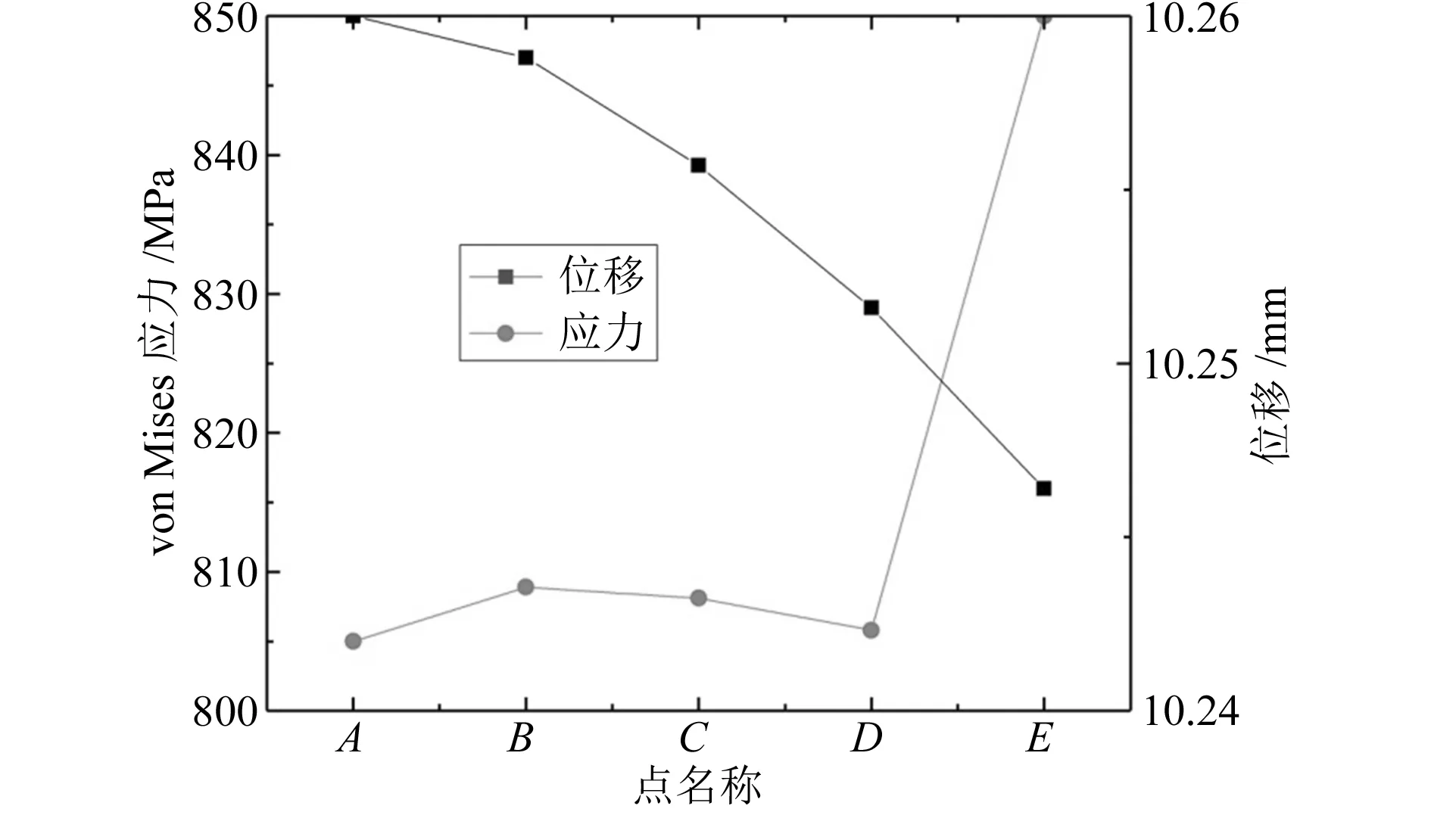
图8 最大位移时5点的位移及应力

图9 可变径球座实物图

4 结论

1)可变径球座在直径不断减小的过程中，其弯曲程度逐渐加大，各处的等效应力也会随之而不断增大，但最终达到的最大等效应力值在材料允许的范围内，满足材料的安全性与可靠性要求，能够确保球座的正确变形。

2)利用可变径球座代替原有的固定球座可以作为解决现有的投球滑套式压裂工具中存在的最大压裂层数受限和投球顺序严苛的问题的一种有效方法。