6-UPS并联机构运动学标定

张学祥，王若冰，刘艳梨,2，杨小龙，吴洪涛

(1.南京航空航天大学机电学院，江苏 南京 210016) (2.江苏安全技术职业学院机械工程系, 江苏 徐州 221011)

与传统的串联式工业机器人的开环结构不同，Stewart并联机构是由并联支链构成的闭环运动系统[1]。相比于串联机构，它具有刚度高、输出力/质量比大、无位置误差累积、重复性好等优势，在运动模拟、隔振技术、并联机床、大型天文望远镜等领域有着广泛的应用[2]。 然而，由于被动铰链数量较多，使得其运动学精度较难保证[3]。并联机构控制器采用机构内部运动学参数来控制机构运动，研究表明，机构铰链及驱动杆的制造和装配误差使得机构内部运动学参数不准确，是导致并联机构的实际位姿与期望位姿产生偏差的主要原因[4]。依靠提高并联机构零部件加工制造精度的方法来提高并联机构位姿精度，会大大提高加工制造成本。相比而言，对装配好的并联机构运动学参数进行标定，是更加经济高效的方法。

标定一般包括运动学参数误差建模、位姿测量、参数辨识和误差补偿等步骤[5]。根据位姿信息的获取方式，可将并联机构的标定方法分为自标定[6]和外部标定[7]。因为自标定需要在被动铰链处安装位移传感器[8]，而本文所标定的并联机构在被动铰链安装传感器比较困难，因而选用外部标定法。

Gao等[9]提出一种利用激光跟踪仪和线性最小二乘法对Stewart机构进行标定的方法，由于并联机构运动学具有非线性，所以该方法辨识得到的个别参数会出现明显的不合理偏差。张文昌等[10]提出一种利用步进迭代法进行运动学误差参数识别的方法，对Delta并联机构运动学误差进行了标定。杨小磊等[11]分别用最小二乘法和Levenberg- Marquardt(LM)算法对6自由度机械臂进行运动学标定仿真，发现LM的辨识效果更好。樊锐等[12]建立了包括虎克铰铰点位置、球铰铰点位置、初始支腿长以及导轨偏转角度在内的54个运动学参数的6-PUS并联机构参数误差模型。Shi等[13]用随机LM对Planar-Delta机构进行了标定，实验结果表明，该算法与传统算法相比具有效率高、精度高、易于实现的优点。

为了提高6-UPS并联机构运动学精度，本文基于前人研究成果，用微分法推导了6-UPS并联机构的运动学参数误差模型，然后分别运用Gauss- Newton(GN)算法和LM进行6-UPS并联机构运动学标定仿真，比较其在有测量误差时的辨识效果。最后用激光跟踪仪和 LM对6-UPS并联机构进行了运动学参数标定实验。

1 误差建模

1.1 6-UPS并联机构的运动学参数

6-UPS并联机构如图1所示，由动平台、基座以及6条支腿构成。支腿采用电动缸驱动，每条支腿上下两端分别通过球铰和虎克铰与动平台和基座相连，可以看作是由6组“万向节副(U)-移动副(P)-球面副(S)”支链并联构成的闭环运动系统。如图1所示，分别采用坐标系O′-x′y′z′和O-xyz表示动平台的体坐标系{A}和基坐标系{B}。上下铰点分别用Ai,Bi表示，i=1，2，…，6。任取6-UPS并联机构的第i个封闭支链O-Bi-Ai-O′满足：

lisi=p+Rai-bii=1,2,…,6

(1)

式中：si为第i条支腿的单位向量；p为{A}到{B}的位置矢量；R为{A}到{B}的姿态矩阵；ai为上铰点Ai在{A}下的位置矢量,ai=[axiayiazi]T；bi为下铰点Bi在{B}下的位置矢量,bi=[bxibyibzi]T；li=Li+Δli，为第i条支腿的长度，Li和Δli分别为第i条支腿的初始长度和驱动增量。

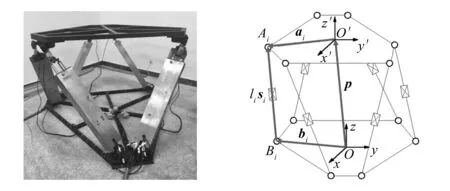
图1 6-UPS并联机构实物图及结构简图

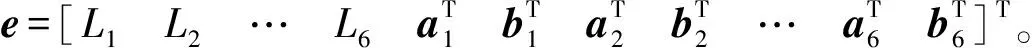
1.2 6-UPS并联机构运动学参数误差模型

6-UPS并联机构的误差建模即为推导机构运动学参数误差与执行端位姿误差的关系式。

(2)

式中：dp=[dxdydz]T，为机构的位置误差；dθ=[dαdβdγ]T,为机构的姿态角误差；dai，dbi分别为上下铰点的位置误差。

联立6条支链的运动学微分方程，提取位姿参数及运动学参数，可将式(2)整理为矩阵形式：

Jxδx=Jdδe

(3)

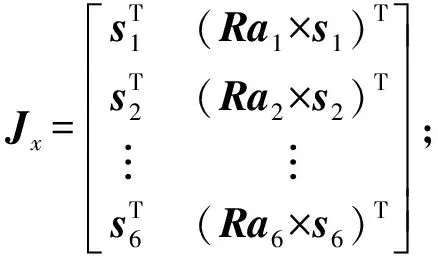
δe为运动学参数误差；δx=[dpTdθT]T，为动平台位姿误差。一般并联机构的雅可比矩阵Jx可逆，则式(3)可整理为:

δx=Jδe

(4)

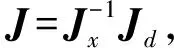
2 辨识算法

6-UPS并联机构正向运动学模型可用支腿驱动位移Δl与对应理论位姿xt之间的映射关系表示为[14]：

xt=f(Δl,e)

(5)

式中：Δl=[Δl1Δl2… Δl6]T。

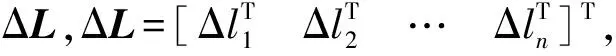
δxj=xrj-xtj=xrj-f(Δlj,e)

j=1,2,…,n

(6)

根据并联机构实测位姿与理论位姿的残差平方和来构造代价函数S(e)[15]：

(7)

运动学参数标定的核心内容即通过最小化代价函数S(e)来估计机构实际运动学参数。这是一个典型的非线性最小二乘优化问题[16]。求解非线性最小二乘问题，最常用的方法是GN，但是该方法当迭代点处的负梯度方向与其迭代方向正交或接近正交时，可能会出现假收敛。LM是对GN的改进，比GN更加稳健，且在迭代初值与真实值差距较大的情况下也能很好地收敛[17]。

对含有运动学参数误差δe的正向运动学模型f(Δl,e+ δe)进行一阶泰勒展开，可得：

f(Δl,e+δe)≈f(Δl,e)+Jδe

(8)

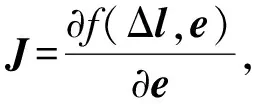
S(e+δe)≈[δX-Hδe]T[δX-Hδe]

(9)

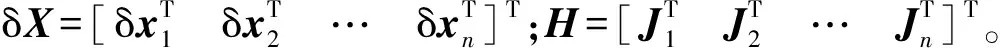
代价函数最小化的必要条件为其导数为零[16]。因此对式(9)求导，忽略二阶偏导项，令结果为零矩阵，可得：

HTHδe=HTδX

(10)

方程左侧的HTH即为忽略二阶偏导项的近似Hessian矩阵。由式(10)可得GN迭代步长δe：

δe=(HTH)-1HTδX

(11)

为保证近似Hessian矩阵的正定性，从而确保δe代表S(e)的下降方向，在HTH添加阻尼项λI(λ>0)，可得LM迭代步长：

δe=(HTH+λI)-1HTδX

(12)

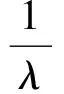
采用LM对6-UPS并联机构运动学参数进行辨识的步骤如下：

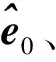
3)计算雅可比矩阵Hk。

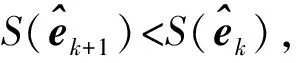
辨识算法流程图如图 2所示。

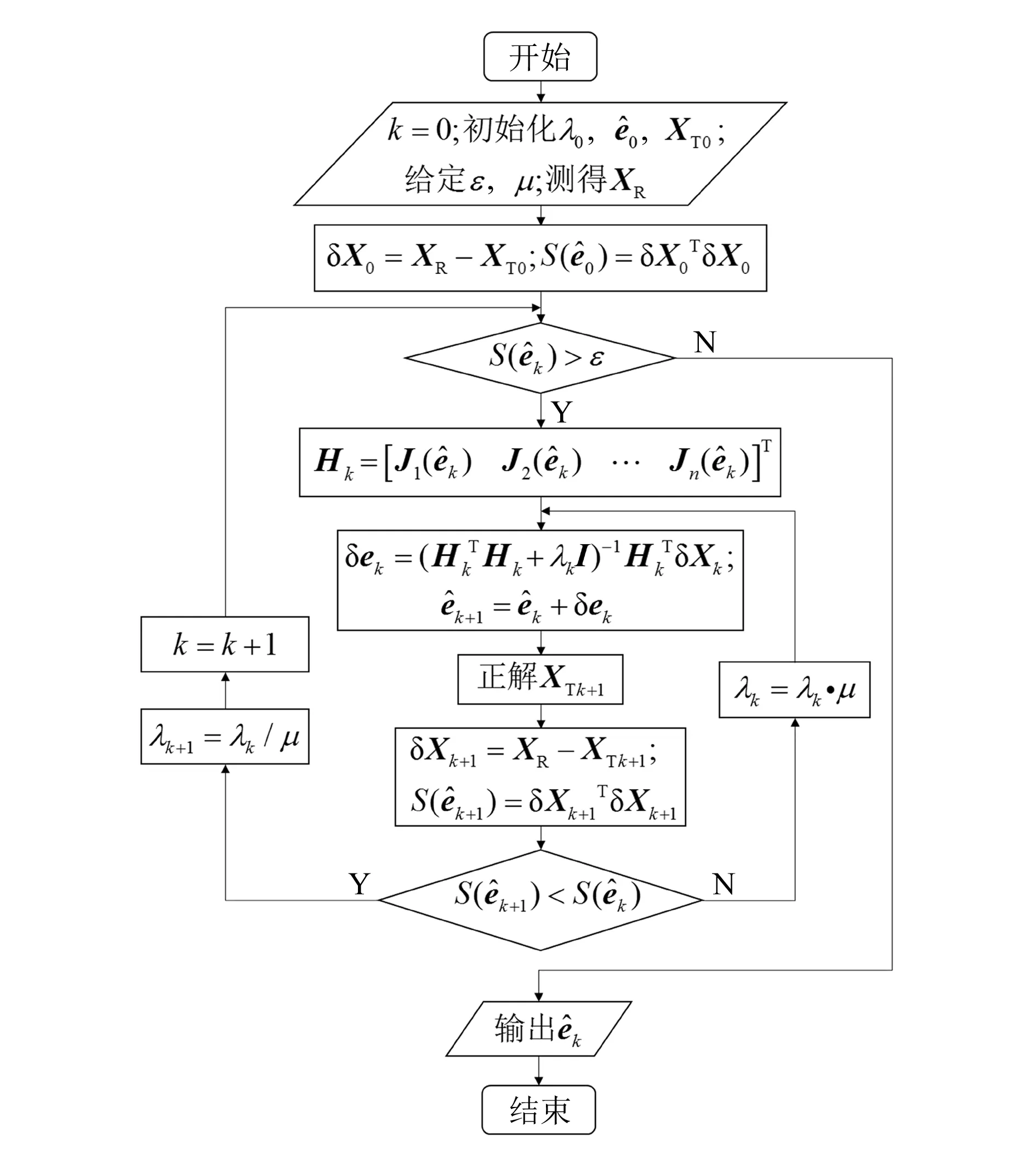
图2 辨识算法流程图

3 仿真实验

Gao等[9]研究表明，标定过程中所测位姿越多、涵盖工作空间范围越广，则误差雅可比矩阵的条件数越小，辨识得到的运动学参数越准确。同时为保证近似Hessian矩阵HTH的可逆性，实验测量组数n需满足m≤6n，m为待辨识的运动学参数数目[12]，即最小实验位姿数目为7。综合考虑实验工作量及所测位姿的涵盖范围，本文在6-UPS并联机构工作空间中选取了64组理论位姿XT0进行实验。

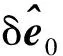
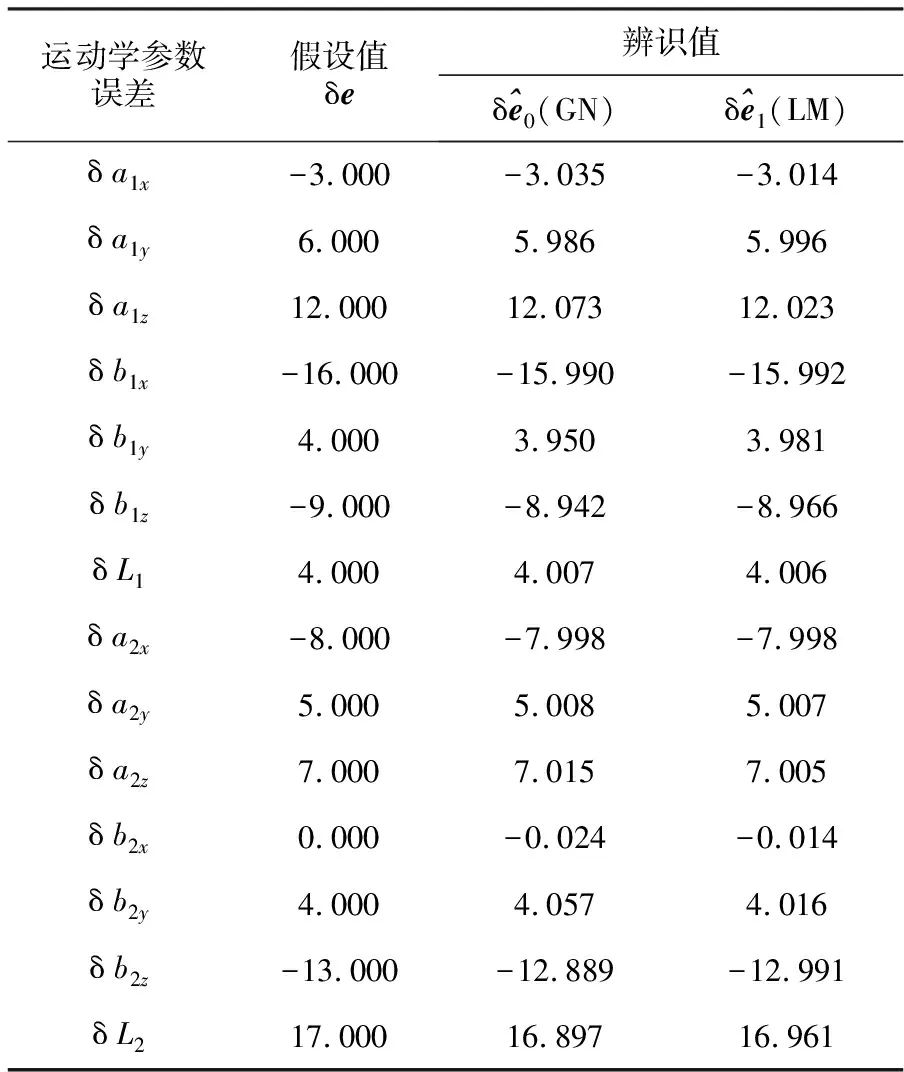
表1 支链1和2运动学参数误差辨识仿真结果 mm

4 标定实验

4.1 实验方案

本文采用faro激光跟踪仪进行位姿测量，其测量精度为16 μm+0.8 μm/m。实验设备如图4所示。在下平台5个参考点上固定靶球基座。用激光跟踪仪测量5个点的坐标，以2点作为基坐标系{B}的原点O，用1，2，3点构造直线作为x轴，用5个点坐标构造xOy平面，以平面法向为z轴，在激光跟踪仪自带测量软件CAM2 Measure中建立基坐标系{B}。用同样的方法可以建立固结在动平台上的动坐标系{A}。

在CAM2 Measure中，可以方便地读取{A}到{B}位置矢量p，姿态角θ则要通过测量两坐标系坐标轴之间的夹角计算求得。记rxy为{A}的x轴与{B}的y轴之间夹角的余弦值，其他符号以此类推，姿态角θ(α,β,γ)的计算公式如下[18]：

图4 实验设备

(13)

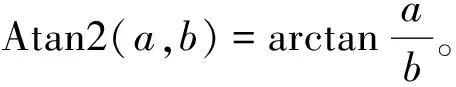
在6-UPS并联机构工作空间中选取64组初始理论位姿XT0，根据机构的理论运动学参数，驱动支腿运动到指定位置。待机构稳定后，利用上述方法可在CAM2 Measure中得到图5所示的64组实测位姿XR。构造残差方程δX0=XR-XT0，用第2节所述算法对机构实际运动学参数进行辨识。

图5 实测位姿

4.2 实验结果

辨识得到的6-UPS并联机构的实际运动学参数见表2。辨识结束后，将并联机构控制器内的理论参数替换为辨识到的实际参数，以达到误差补偿的目的。

为了观察标定对机构定位精度的提升效果，随机选取25组位姿进行验证，针对每组位姿，分别根据机构的理论参数和辨识参数驱动支腿运动到指定位置，用激光跟踪仪分别测量实际位姿。比较测得的实际位姿与理论位姿的误差，位置误差Position_error和姿态误差Orientation_error计算公式定义如下[15]：

(14)

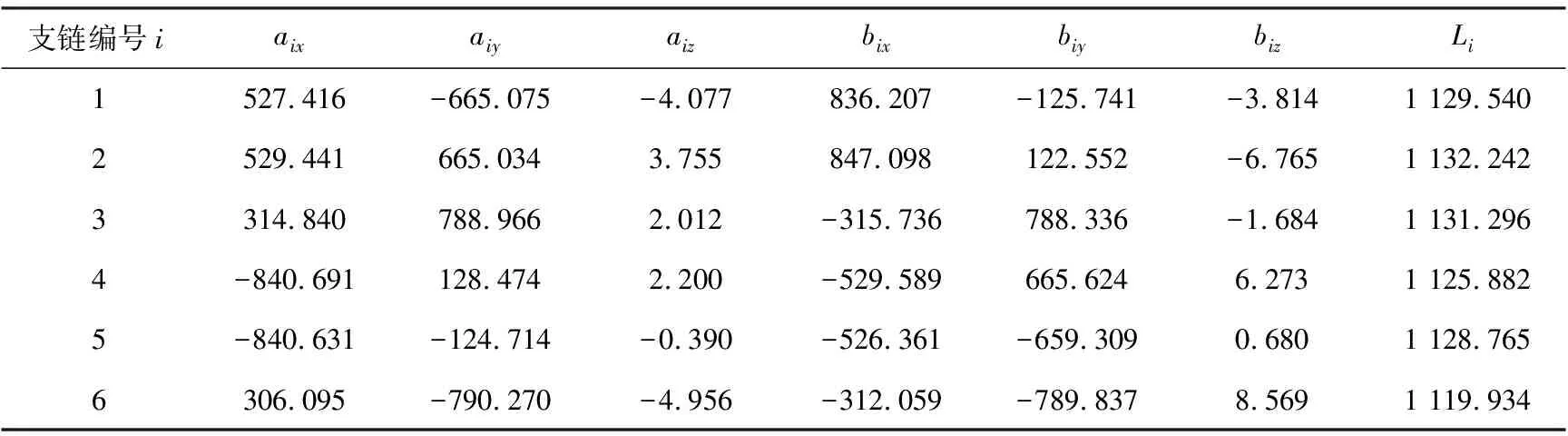
表2 6-UPS并联机构运动学参数 mm

式中：xt和θt为随机选取的理论位置和姿态；xr和θr为实际测得的位置和姿态。

图6和图7分别展示了标定前后的各组位姿的位置误差和姿态误差。从图中可以看出，标定后位置误差的范围由7～10 mm降低到0～0.3 mm，姿态误差的范围由0.20°～0.45°降低到0～0.025°；位置均方根误差由8.512 mm降低到0.178 mm，姿态角均方根误差由0.330°降低到0.012°。由此可见，标定后机构的运动学精度提高了一个数量级以上。

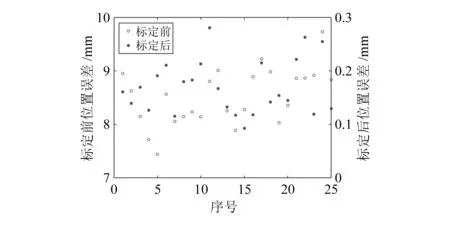
图6 标定前后的位置误差

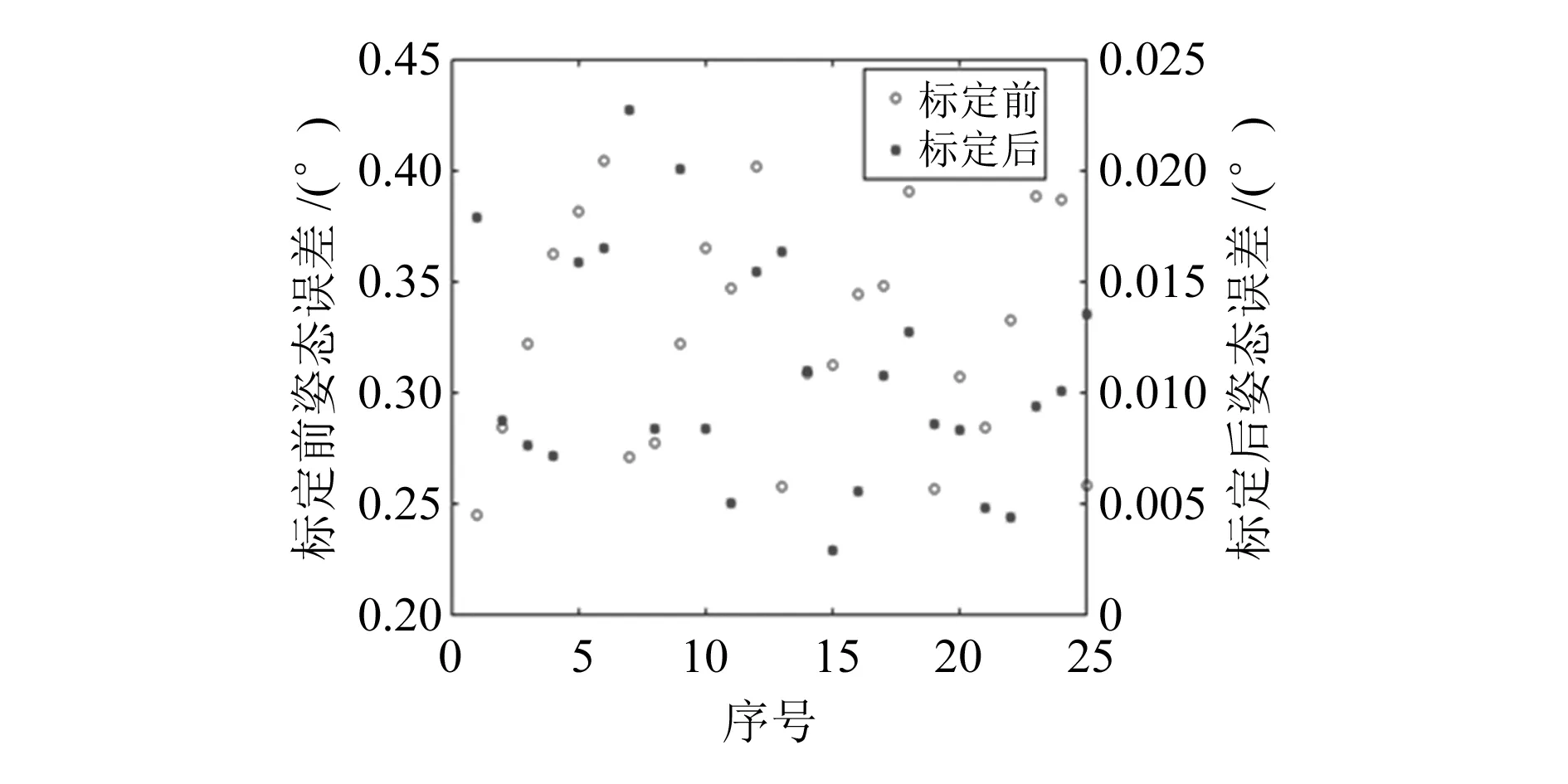
图7 标定前后的姿态误差

5 结论

本文针对6-UPS并联机构进行了外部标定，得到如下结论：

1) 本文所用的对支链约束方程取微分推导运动学参数误差模型的方法具有通用性，可用于其他构型并联机构的运动学参数误差模型的推导。

2)用 LM能够准确辨识出并联机构运动学参数，且辨识效果优于GN。用辨识得到的运动学参数对并联机构进行误差补偿，使得机构的位置精度和姿态精度都提高了一个数量级。