模糊故障树在船舶柴油机滑油系统故障诊断中的应用

青岛远洋船员职业学院 贾广付

故障树分析法是针对复杂设备进行故障寻查的一种技术，这种分析法得到了世界上的广泛认可。故障树分析法最初是由贝尔实验室首先应用的，故障树分析法通过建立树状的逻辑图，把故障从上至下进行梳理，通过逐条顺序的进行查找，以迅速确定故障的原因，进而提升故障确认、检测和修复的速度，从而增加船舶的安全性，推进智能船舶柴油机的发展。传统的故障树理论是把故障理想的划分为发生或不发生两种情况，但是在实际的使用过程中，由于人为因素对故障的发生起着重要作用，同时对于一些较为复杂的故障事件，无法简单的用故障和正常来进行划分。于是在故障树研究时，把模糊数学的理论引入进来，因而形成了模糊故障树理论。模糊故障树拓展了传统故障树的内涵，使适用范围大大拓展，同时计算的精度也得到了提高。对于船舶柴油机来讲，人为因素占所有故障树的比例高达52%，因此模糊故障树分析法应用到柴油机故障分析中，有助于给柴油机维修保养提供更适用的意见。

模糊故障树的核心思想就是故障发生的概率不是精确值、固定值，而是模糊值。通过底事件故障概率模糊化，门的模糊化以及主观事件的模糊化，运算的法则运用模糊数学的拓展原理来进行定性定量分析。

1 模糊故障树的方法类别

1.1 底事件故障概率模糊化

故障树定量分析的依据就是底事件发生的概率，底事件概率的获取有三种方式。但是每一种方法都有一定的不完整性，不能获取准确无误的故障发生的概率数据。因此在模糊故障树中，为了更有效的获取故障发生的概率，并降低获取的难度，采取了模糊数来表示故障发生率。并且在应用中可以依托使用者的经验，适用性更强。

1.2 门的模糊化

在实际故障分析中，每个事故原因相互之间的关系并不是都能清晰的表示出来。各个事件原因相互关系比较模糊，存在着不确定因素。因此，很多时候我们就很难就传统的门来进行构建故障树。在模糊故障树中，就依据模糊逻辑构建了模糊门算子。这样在进行构建模糊故障树时就用模糊门算子来表示各事件之间的关系。

1.3 主观事件模糊化

根据以往柴油机故障性质的统计分析可以看出人为因素在柴油机故障中所占的比例非常高，因此在分析柴油机故障时必须要考虑到人为因素。底事件根据故障的性质划分为主观事件与客观事件。客观故障事件的概率可以由已发生的故障统计数据获取，主观故障事件的概率则用模糊数来表示，两者都融入到故障树分析中去。

2 模糊集和隶属函数

2.1.模糊集

当研究的事物本身就难以准确界定其概念，事物本身所就有的不确定性就称之为模糊性。模糊数学就是来研究这种不确定的模糊现象的。把经典集合加以拓广，把经典集合中的特征函数μA（u），的取值从值域{0,1}拓展到[0,1]，相应的我们把集合A拓展到模糊集A，特征函数μA（u）就相应的拓展为μA（u），即特征函数拓展为隶属度函数（简称隶属函数）。

模糊子集：给一定义域U，U 在闭区间[0,1]的所有映射μA

μA的数值体现了u 对于模糊子集的从属程度。μA的数值与1 越是相近，u 对模糊子集的从属程度越高。反之，μA的数值与0 越是相近，u 对模糊子集的从属程度越低。

模糊集合A 内有任意的两个点x，y∈A，同时λ∈[0,1]连接x，y 两点线段上一点Z，其中，z=λx+（1-λ）y，满足下面的不等式：

即点z 居于x，y之间，并且这条直线与集合A 的交点有两个。

符合上面条件关系的集合A 称之为凸模糊集合。如何存在点x0使μA（x0）=1，那么集合A 为正规模糊集。

如果A 为实数域中的正规模糊集，并且所有闭区间λ∈[0,1]都有A=[aλ，bλ]，A 被称为模糊数。

2.2 三角模糊数

工程机械中的模糊故障树使用种类一般为正态、梯形以及三角模糊数。其中三角模糊数计算比较简单，计算结果的精度也能符合要求，所以，本文重点讲解三角模糊数。

三角模糊数的表示

假定论域U 为实数域，p 代表三角模糊数，μp（x）为隶属函数，用公式表达：

三角模糊数P 就能够通过三个参数（a，m，b）进行表示，表示为P=（a，m，b）。

三角模糊的运算

把实数集R 通过二元运算“*”变换成R 的模糊集合，于是：

通常在实际运算中会使用一下运算法则：

模糊数“+”运算

（p1+p2）（z）=（a1,m1,b1）+（a2,m2,b2）=（a1+a2）+（m1+m2）+（b1+b2）

模糊数“一”运算

1-p（z）=1-（a,m,b）=（1-b,1-m,1-a）

（p1-p2）（z）=（a1,m1,b1）-（a2,m2,b2）=（a1+b2）+（m1+m2）+（b1+a2）

模糊数“×”运算

（p1×p2）（z）=（a1,m1,b1）×（a2,m2,b2）=（a1×a2,m1×m2,（b1×b2）

3 模糊故障树中的门算子与重要度

以传统故障树的各种门算子为基础，应用模糊理论得出模糊门算子。

3.1 模糊与门

传统故障树把所有故障发生的概率都进行精准确认，故障i发生的概率是精确值，与门算子定义：

事件i 的概率不是精确值pi，而是模糊数pi时，并且pi=（ai,mi,bi），模糊数与门则是：

3.2 模糊或门

或门在传统故障树中的定义为：

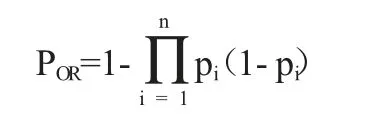
同样当事件i 的概率不再精确，而是模糊数pi时，模糊或门的算子为：

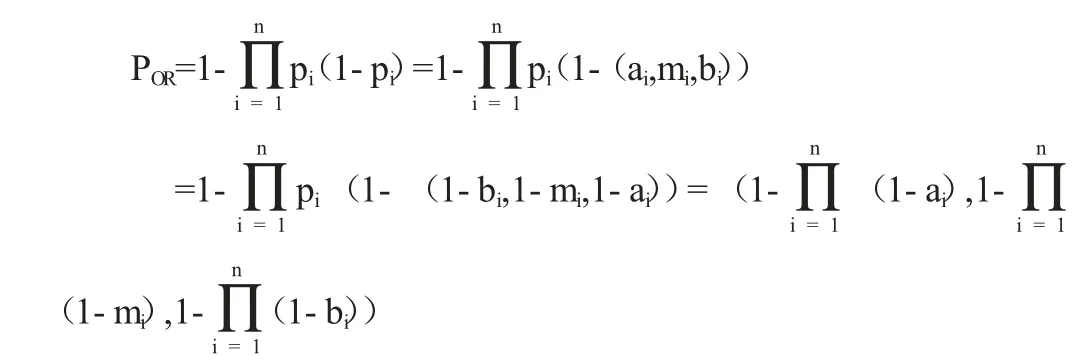
3.3 模糊非门

PNFG=1-p=（1-b,1-m,1-a）

3.4 模糊重要度

在实际工作生产中，很多时候是无法得到足够多的数据，相当一部分的可靠性指标是不精准的，是模糊的，因此很难应用以往的重要度分析方法。通过把模糊均值的概念应用到重要度的计算中来。也就是使用模糊均值来计算模糊概率的重要度。模糊均值的定义不是统一的，而是有比较多种方法。本文介绍中值法的定义。

假定A 为有界模糊数，并且A 在区间[a,b]之间满足：

4 模糊故障树模型建立规则

应用概率论的有关知识将故障树中的各个事件求出来，一旦确定了底事件出现的几率和结果函数，顶事件概率也就确定了。如果得出的底事件概率结果为模糊概率，则出现的第一个异常现象的几率也应该在相应的范围内取值。对故障树中各个故障事件的概率进行计算时，计算越简单误差便会越小，因此为了保障计算结果的准确性，保证质量安全，以下给出了几个模糊数模型优先选择的条件

4.1 在计算底事件的模糊概率时，应该尽可能的同真实情况想接近。

4.2 尽量的简化计算过程，计算量不能太大。

4.3 利用四则运算计算出的模糊概率的数学结构同前面的相比不能更复杂。

4.4 经过多次基本数学运算得到底事件的模糊概率，这个概率出现的误差必须在诊断要求之内，通常情况下我们说的复杂主要指的是运算转移的复杂。

将计算得到的误差累加，也就是上一级同下一级的误差相加，这样一级一级的叠加之后同实际结果之间会出现较大的偏差，计算也就失去了原来的意义。实际使用中最常用的计算方式是三角形模糊数，经过四则云端之后保证其数学表达式不会发生任何变化，误差也要在允许的范围之内。

5 滑油系统模糊故障树模型建立

柴油机所有的相互运动部件都需要滑油的润滑，如果滑油系统出现故障，将会对柴油机造成损坏。滑油系统的故障根据第三章所列的有压力过低、消耗过快、油温过高、油质较差、气缸润滑故障等几个方面。

滑油压力过低的原因：X1 滑油泵故障、X2 油底壳油位过低、X3 滤器脏堵、X4 冷却器脏堵、X5 大风浪天气吸入空气、X6 轴承间隙过大等。

引起滑油消耗过快的原因：X7 活塞环磨损过大、X8 滑油系统泄漏等。

引起油温过高的原因有：X9 滤器脏堵、X10 冷却器脏堵、X11 调温三通阀故障、X12 油底壳油位过低等。

引起油质较差的原因：X13 分油机故障、X14 燃烧质量不好、X15 活塞填料函故障、X16 活塞环故障、X17 滑油冷却器故障等。

引起气缸润滑故障的原因：X18 气缸注油器故障、X19 流量传感去故障、X20 气缸油箱油量过少、X21 马达故障。

6 滑油系统模糊故障树分析

下表列出了某轮柴油机连续工作了1000 小时后的滑油系统基本事件模糊数。其中，基本事件模糊数与工作时间有着紧密的关系。因为随着柴油机工作时间的增加，各个部件的性能或逐渐下降，使得整个系统的性能也下降。某轮滑油系统基本事件模糊概率Px，（a,m,b） 分 别 为：X1 (0.004,0.006,0.01)；X2 (0.001,0.013,0.014)；X3(0.036,0.040,0.50)；X4 （0.01,0.012,0.016）；X5 （0.004,0.007,0.009）；X6（0.003,0.005,0.008）；X7 （0.015,0.018,0.020）；X8（0.01,0.013,0.015）；X9（0.016,0.018,0.020）；X10（0.012,0.015,0.018）；X11；（0.016,0.018,0.020）；X12（0.015,0.016,0.018）；X13（0.01,0.012,0.015）；X14（0.005,0.006,0.008）；X15（0.004,0.006,0.007）；X16（0.008,0.010,0.012）；X17（0.009,0.012,0.015）；X18（0.01,0.013,0.015）；X19（0.006，0.007,0.009）；X20（0.005,0.006,0.008）；X21（0.01,0.012,0.014）。

顶事件滑油系统在柴油机连续工作1000 小时后故障发生的概率（0.209,0.265,0.321）。这表明滑油系统在柴油机连续工作1000 小时后，发生故障的概率介于0.209 与0.321 之间，并且0.265 的概率值最大。

底事件的模糊均值分别为0.007；0.012；0.042；0.013；0.007；0.010；0.0177；0.0127；0.018；0.015；0.018；0.0163；0.0123；0.0063；0.0057；0.010；0.012；0.0127；0.0073；0.0063；0.012。通过故障树模糊重要度排序，在查找滑油系统故障时更有针对性。