双螺杆啮合元件与反螺纹元件对流场影响的仿真
2020-06-20韩海川刘谨李开国孙亮姚爱英陈占春
韩海川 ,刘谨 ,李开国 ,孙亮 ,姚爱英 ,陈占春
(1.太原理工大学机械与运载工程学院,太原 030024; 2.太原理工大学煤矿综采装备山西省重点实验室,太原 030024)
聚合物材料由于其成本低、易改性等特点,在汽车、家电等领域都有广泛的应用。为满足人们生产生活所需,聚合物通常需要多种材料共混改性,从而制备出符合韧性、硬度等要求的材料。啮合同向双螺杆挤出机是最常见的聚合物共混加工设备[1],其中的螺杆结构由螺纹元件、捏合盘元件和反螺纹元件等单个元件通过花键组合连接而成,而不同的组合结构会对熔体流场产生不同的混合效果。
王飞等[2]从力化学反应器的新型螺杆与料筒的配合结构入手,在料筒内壁与螺杆外表面开设内齿与螺棱隔断,通过数值模拟对物料的剪切速率、运动速度和压力等的分析,发现开设内齿的新型料筒螺杆结构比普通强剪切挤出机剪切效率提高了67%;张帅等[3]利用Polyflow 软件对螺杆与料筒不同的断面形状组合进行了模拟研究,研究发现了螺杆与料筒螺槽断面形状都为梯形时剪切效果更好;张鹏等[4]对螺棱梯形底角和凹槽半径进行了数值模拟,发现螺杆界面梯形底角为60°且凹槽半径为1.5 mm 时,螺杆的剪切效果最好;I. Manas-Zloczower 等[5]得出,错列角和长度一定时,捏合盘厚度增加,它的分散混合能力变强而分布混合减小;J. I. Orisaleye 等[6]开发了设计螺杆挤出机的分析模型,推导出了螺杆最佳通道深度和螺旋角的表达式,可以有效预测螺杆挤出机的性能;胡东东等[7]系统分析了捏合盘厚度、错列角等参数对流场的影响,并分析出各项参数下的混合规律。沈晓斌[8]等人设计了圆弧齿廓代替渐开线齿廓的双螺杆磨浆机,增大了设备的传动功率,提高了效率。
国内外学者们对啮合同向双螺杆进行了许多较为深入的研究[9-11],多集中在对捏合盘不同结构的分析中,还不足以全面分析螺杆中的混合情况。笔者针对螺杆中对流场影响显著的元件捏合盘和反螺纹,利用粒子示踪方法,研究粒子在不同元件组合的螺杆中的混合情况,通过统计分析,比较其分散混合与分布混合的规律。
1 理论模型
1.1 有限元模型
根据搭建同向双螺杆的几何学原理[12],建立常规双螺杆Ⅰ、带有反螺纹的双螺杆Ⅱ、带有捏合盘的双螺杆Ⅲ(下文以Ⅰ、Ⅱ、Ⅲ表示)的三维模型,如图1 所示。
螺杆外径为16.6 mm,内径为13 mm,每个元件导程为30 mm,每个捏合盘厚度为5 mm,错列角为72°,螺杆中间挖空便于网格划分和数值计算。

图1 双螺杆的有限元模型
1.2 数学模型
(1) 模拟假设。
在模拟过程中,根据聚合物的性质和熔体在混合段的输送情况,可以做以下的假设:
①壁面无滑移;②流体为不可压缩的非牛顿流体;③相较于流体的粘滞力可以忽略惯性力和重力的作用。
(2)模拟方程。
根据以上的假设条件,描述流体的方程如下:
连续性方程:▽v=0
流体本构方程:

式中,v为速度矢量,m/s;P为静压力,Pa;τ为剪切应力张量;η为表观黏度,Pa·s;η∞为无限剪切速率下的黏度;η0为零剪切黏度,Pa·s;λ为松弛时间,s;γ为剪切速率,s–1;n为非牛顿指数。
为了便于粒子示踪的观察和分析,模拟中采用质量比为50 ∶50 的线型低密度聚乙烯(PE-LLD)与苯乙烯–丁二烯–苯乙烯共聚物(SBS)混合流变值[13],见表 1。

表1 Bird-Carreau 粘度模型参数
2 数值模拟
2.1 建立有限元模型
将三维模型导入到Gambit 中进行有限元网格的划分,螺杆采用非规则型(TGrid)四面体单元(Tet/Hybrid)划分网格。流体流动的区域流体域采用六面体(Hex)类型单元和规则性网格划分方法(Map),如图2 所示。其中啮合区域是混合发生的地方,网格需要细划以增加计算结果的可靠性。

图2 流体域网格模型
2.2 模拟参数设定
在瞬态任务中,螺杆转动过程会带来网格重复划分从而增加计算量的问题。而在Polyflow 中具有网格重叠技术(MST),可以自动将螺杆与流体域的网格进行组合生成,方便计算。
设定螺杆转速为100 r/min,每隔0.05 s (一个时间切片)螺杆转动30°取一个结果值储存,共储存6 个结果也就是螺杆转动180°回到初始位置时刻。流体域入口压力为0,出口压力为1 MPa。用Picard 插值进行黏度迭代计算。
3 结果分析
混合过程是将聚合物的非均匀性趋于均匀的一种物理混合方式,各组分并没有改变其本质。而混合指标是衡量螺杆工作效果的重要参数,其中主要包括:分散混合,通过外力减小粒子尺度并使其分布均匀;分布混合,在不改变粒子尺度的情况下使其在空间中均匀分布。
在流体域的入口处放置1 000 个粒子进行混合任务的计算,将模拟结果在Polystat 中读入,通过函数计算统计并观察粒子的混合及分布情况。
3.1 分散混合
(1)剪切应力分布。
剪切应力能很好反映粒子在混合过程中所经历的受力情况。计算粒子可能经历的所有剪切应力值,并统计所经历某一剪切应力值及以下的粒子个数占所有粒子的百分比,记此剪切应力值为最大剪切应力值[14]。统计结果如图3 所示。

图3 剪切应力分布图
从图3 可看出,三种螺杆中最大剪切应力分布的趋势大致相同,常规螺杆最小的剪切应力大约为0.07 MPa,带反螺纹的螺杆为0.125 MPa,带捏合盘的为0.075 MPa。在相同的粒子百分数情况下,带有反螺纹的Ⅱ中粒子经历的最大剪切应力最大,带有捏合盘的Ⅲ中次之,常规螺杆Ⅰ中最小。而在分布曲线的末端,Ⅰ中所有粒子经历的最大剪切应力值在0.4 MPa 处已经结束;Ⅲ中还有少量粒子经历的最大剪切应力值仍在增加,大约可以接近到0.5 MPa;而Ⅱ中仍有相当一部分粒子经历着更高的最大剪切应力,大约为0.9 MPa。
根据统计曲线分布情况,具有反螺纹和捏合盘的组合螺杆结构剪切效果更好,具有反螺纹结构的螺杆在正向螺纹与反向螺纹交汇处,反螺纹可以阻挡粒子的正常输送,并且在螺杆转动过程中给粒子一个反向的剪切应力,在正向螺纹与反向螺纹的共同剪切下形成了更大的剪切应力,比常规螺杆的剪切应力提高了近78%。
由于粒子所经历的最大剪切速率与最大剪切应力分布曲线趋势相同,因此不再赘述。
3.2 分布混合
(1)分布指数。
将粒子随机的分布在流体域三维空间中,记此时的随机分布为粒子的最优分布,然后将每个计算结果的粒子分布情况与最优分布作比较,差异越小则证明粒子混合状态越好。分布指数统计如图4 所示。

图4 分布指数统计图
图4 中每个时间切片为0.05 s,共200 个切片。加有反螺纹的螺杆Ⅱ在起始阶段粒子混合与最优解有一段差异减小的过程,大约在第四个时间切片的时候,随着螺杆工作时间的增加,Ⅱ中的粒子分布指数出现剧烈的波动且大幅增加。反螺纹结构使粒子产生了回流阻碍了粒子继续沿轴向的分布,与随机分布在整个流体域空间的最优解粒子差异增大。带捏合盘螺杆Ⅲ与常规螺杆Ⅰ中粒子在第50 个时间切片处就已经在整个流体域空间中分布均匀,而带有反螺纹的螺杆Ⅱ中在第150 个时间切片处曲线才趋于最小,其粒子在整个空间的分布才相对均匀。
因此,带有反螺纹的螺杆在空间分布时间上相对滞后,增加了粒子在挤出机内的停留时间宽度,这种特性适用于反应挤出实验中。
(2)分离尺度。
建立粒子的浓度场,设置入口处左半边的粒子浓度为1,右半边粒子浓度为0,分别代表不同的粒子[15],粒子经过螺杆的剪切混合之后在出口处的分布状态,如图5 所示。

图5 粒子入口(左)、出口(右)
示踪粒子在向前输送时,不断被螺杆掺混,分离尺度也由最初入口两侧不断减小,统计图如图6所示。
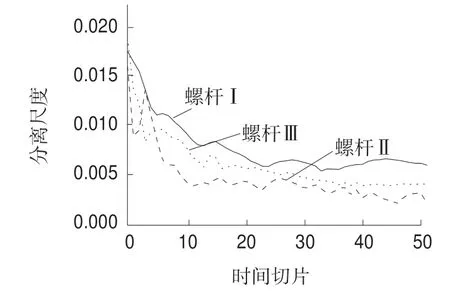
图6 分离尺度统计图
时间切片后半段分离尺度的变化趋势不大,因此只取前50 个时间切片用来分析。
通过分离尺度可以得到径向平面粒子间的混合情况。可以看到常规螺杆中分离尺度下降趋势相对较缓,当曲线平稳时,两种组合螺杆的分离尺度要比其小,证明其径向平面的粒子间经过螺杆的剪切混合,两种粒子的间距减小。带有反螺纹的螺杆Ⅱ的分离尺度达到最小,能够达到常规螺杆中粒子分离尺度的1/2。在回流与多次剪切下,带有反螺纹结构的螺杆使得径向平面的粒子掺混均匀,其优异的径向混合效果是常规螺杆的2 倍。
4 结论
通过建立不同元件在啮合同向双螺杆中的三维组合模型,使用Polyflow 对PE-LLD 和SBS 混合熔体在三维模型中进行转动剪切模拟,最后利用粒子示踪统计方法,分析不同模型的分散、分布混合规律,得出结论:
(1)两种组合结构的螺杆剪切效果优于常规螺杆,并且在组合螺杆中,带有反螺纹的螺杆剪切力最大,比常规螺杆提高了约78%,其所具备的分散混合能力更强;
(2)在空间分布混合中,反螺纹的回流现象阻碍了粒子在空间中的分布混合,这种反流的特性增加了粒子的停留时间,可以应用于反应挤出中。而常规螺杆与带有捏合盘的螺杆中粒子的空间分布混合较快,并且二者的分布指数趋势大致相同,在工程实验中的表现不会有太大差异;
(3)径向平面中粒子的分离尺度,两种组合螺杆的混合情况要比常规螺杆好。带有反螺纹的螺杆在回流与强剪切的作用下,使得径向平面中不同粒子均匀的掺混,大大提高了粒子间的混合效果,其粒子径向混合效果是常规螺杆的2 倍。
综上所述,在实际生产中双螺杆中的每一种元件对挤出流场的影响不同,进而影响整个螺杆的挤出分散效果。通过计算机模拟PE-LLD/SBS 材料在不同螺杆结构中的混合分散效果及规律,可以有效指导啮合同向双螺杆挤出机的螺杆元件搭配设计以及聚合物的生产加工。
