机器人导航路径的动态分级蚁群算法规划策略

王槐彬，彭 雪，周诗源，夏小云

（1.广东交通职业技术学院，广东 广州 510650；2.广东技术师范大学，广东 广州 510665；3.嘉兴学院，浙江 嘉兴 314001）

1 引言

随着人工智能技术的迅猛发展，以移动机器人为代表的智能生产和智能服务正加速形成。而机器人应用环境的多样性、复杂性对机器人路径规划方法提出了更高要求[1]，因此研究机器人路径规划方法具有指导意义和实用价值。

机器人路径规划的早期成果主要为静态环境下全局路径规划，常见的方法有栅格法、可视图法、A*算法等，此类算法原理简单、规划效率低，之后的研究主要是对这几类方法的改进或方法的结合；当静态环境下全局路径规划无法满足机器人实际应用时，出现了各类仿生算法应用于机器人路径规划，一直延续至今仍是机器人路径规划研究的主要方向和热点。文献[2]提出了改进人工势场算法，解决了目标不可达、局部极值问题，同时降低了算法计算量并提高了路径平滑度；文献[3]提出了变参数萤火虫算法，并应用于Maklink路径的二次优化，在一定程度上减少了路径长度；文献[4]提出了多目标遗传算法，并将其应用于对双焊接机器人协调路径求解，得到了双焊接机器人最佳路径。以上研究成果对机器人导航技术都起到了一定的促进作用，随着算法性能的提高和硬件的发展，机器人路径规划技术仍有较大的研究空间。

研究了静态环境下全局路径规划问题，建立了工作环境的蜂巢栅格模型，相比于方形栅格的转弯角度和避障路径比有所减小；提出了动态分级蚁群算法并应用于路径规划中，达到了提高路径质量和减少算法运行时间的目的。

2 蜂巢栅格模型

2.1 蜂巢环境模型

蜂巢栅格是参考传统方形栅格的思想加以改进而提出的，如图1所示。使用边长为的蜂巢栅格将机器人工作环境进行分割。对蜂巢栅格内的障碍物叠加上机器人半径，从而可以将机器人视为一个质点。使用传统方形栅格的膨化处理方法，未满一个栅格的障碍物将其膨化到整个蜂巢栅格内。障碍物栅格赋属性值为“1”，不含有障碍物的栅格赋属性值为“0”。

图1 蜂巢栅格模型Fig.1 Honeycomb Grid Model

2.2 蜂巢模型与栅格模型对比

从转向角和避障路径比两个方面对方形栅格和蜂巢栅格模型进行比较。

（1）转向角。机器人遇到障碍物时，传统方形栅格转向时的转向角为90°，而蜂巢栅格的转向角为30°，说明使用蜂巢栅格的避障转向角较小，路径更加平滑，可以提高机器人运动的安全性，如图2所示。

图2 两种栅格比较Fig.2 Comparation of the Two Kind of Grids

（2）避障路径比。将避障路径比定义为：机器人避开单位长度的障碍物需要绕行的距离。红色实线为直线行驶时的碰撞路线，黑色实线为避障路线，如图2所示。则对于方形栅格来讲，避障路径比为，蜂巢栅格的避障路径比为由此可以看出，传统方形栅格避开单位长度的障碍物需绕行1.414单位距离，而蜂巢栅格避开单位长度的障碍物只需绕行1.155单位距离，因此从避障路径比的角度讲，蜂巢栅格优于方形栅格。

（3）使用 ACS蚁群算法[5]分别在（30×30）的方形栅格地图和蜂巢栅格地图上进行路径规划，ACS蚁群算法原理在下节中给出，规划出的路径和路径长度随迭代次数的变化过程，如图3所示。

图3 两种栅格的路径比较Fig.3 Path Comparation of the Two Kind of Grids

对比图3中的3幅图，可以看出，在蜂巢栅格环境下规划出的路径明显比方形栅格环境下更加平滑。由图3（c）可以看出，蜂巢栅格环境下的路径短于方形栅格环境下的路径，且收敛时的迭代次数略少于方形栅格环境，因此从路径长度和平滑性角度讲，蜂巢栅格模型优于方形栅格模型。

3 ACS蚁群算法

3.1 路径选择概率

在ACS蚁群算法中，蚂蚁由城市i到城市j的选择方法使用伪随机概率进行构造，即：

式中：S—蚂蚁最终选择的城市；allowedi—城市i的可选城市；τij—城市ij间的信息素浓度；α—信息素因子；ηij—城市ij间的启发信息，在旅行商问题中设置为城市ij间距离的倒数，在这里设置为城市j与目标点距离；β—启发信息因子；q0—（0，1）间的一个常数；q—（0，1）间的随机数；当 q≤q0时使用式（1）中的伪随机比例公式选择下一城市j，当q>q0时使用轮盘赌[6]选择下一城市j，即：

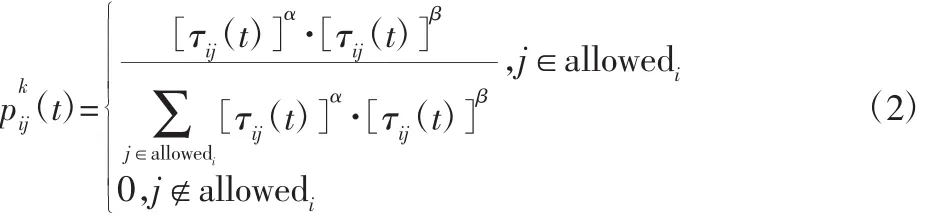
3.2 局部与全局信息素更新

信息素更新方法分为局部信息素更新和全局信息素更新两种。局部信息素更新是蚂蚁每完成一次城市选择就对相应的路径信息素进行更新，这种对所有蚂蚁走过路径均进行信息素更新的方法可以减小路径之间的信息素差异，增强算法的多样性，提高算法全局搜索能力。局部信息素更新方法[7]为：

式中：ρ—信息素挥发率；τ0—信息素初始值。

全局信息素更新是所有蚂蚁完成一次迭代后只对最优路径上的信息素进行更新，这种信息素更新方式会逐渐拉大较优路径与较差路径上的信息素浓度差距，促进算法收敛，但是却容易陷入局部最优。全局信息素更新方法[8]为：

式中：Δτij—路径ij上信息素增量；Lop—最优路径长度。

4 动态分级蚁群算法

4.1 动态分级策略

在人工蜂群算法中，根据蜜蜂的适应度将蜂群划分为引领蜂、跟随蜂和侦查蜂三个等级[9-10]，参考这种分级思想，将蚁群分为寻优蚁和侦查蚁两个等级，其中适应度靠前的蚂蚁定义为寻优蚁，使用较大的信息素因子α，突出较优路径上信息素对蚂蚁的引导作用，促进算法收敛；适应度靠后的蚂蚁定义为侦查蚁，使用较大的启发信息因子β，突出启发信息对蚂蚁的牵引作用，负责开发较优路径之外的路径，寻找更多优质解而提高解的质量。动态分级算子设置为：

式中：Lop—最优路径长度；Lk—蚂蚁k的路径长度；f（Lk）—蚂蚁k的适应度函数。

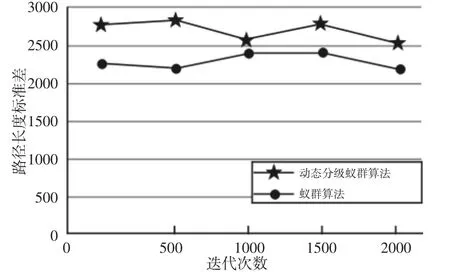
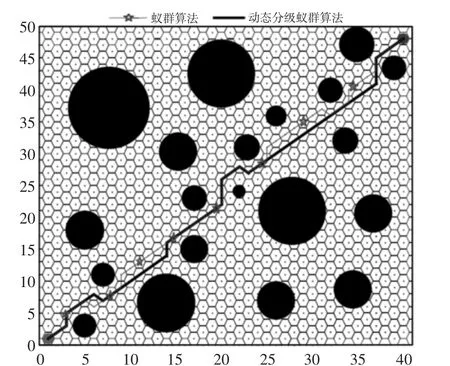
设置一个侦察蚁与寻优蚁的分级阈值M∈（0，1），当0

4.2 信息素动态加权更新

前文中已经分析，局部信息素更新能够较小路径间信息素差异，增强算法多样性，但是收敛性不足；全局信息素更新能够增大不同路径间信息素差异，提高算法收敛性，但是易收敛于局部最优。为了同时兼顾局部信息素更新和全局信息素更新的优势，提出了信息素动态加权更新策略，使寻优蚁和侦察蚁执行不同权重的信息素更新策略，为：

式中：Δτij—路径 ij上的信息素增量；—蚂蚁k经过路径ij时产生的信息素增量；N—蚂蚁规模；λ1>λ2>0—加权系数。

当蚂蚁为寻优蚁时，使用式（6）中的第二式更新，也即使用较大的权重λ1更新信息素，同时路径越优则适应度函数f（Lk）也就越大，通过加权和适应度函数的构造方式，使越优路径上的信息素越浓。当蚂蚁为侦察蚁时，使用式（6）中的第三式更新，通过小权重和小适应度值使较差路径上信息素浓度较低。由以上分析可知，这种信息素更新方式，即使用了局部信息素更新中的全部蚂蚁更新，减小了路径间信息素的差异，同时也参考了全局信息素更新中的有差异更新思想，保证了较优路径上具有更浓的信息素。加权系数λ1、λ2不可相差太大，否则会失去分级加权的意义。经过大量实验验证，当λ1=4、λ2=2时算法搜索性能最佳。

4.3 蚁群混合与重新分级

在算法的第一次迭代过程中，蚁群按照传统的ACS算法进行。之后每完成一次迭代就将所有蚂蚁混合，按照搜索的路径适应度进行重新分级，这样能够保证“表现进步”的侦查蚁升级为寻优蚁，而“表现后退”的寻优蚁降级为侦查蚁。通过这种方式确保较优路径全部在寻优蚁群中，充分发挥较优蚂蚁信息素对其他蚂蚁的引导作用。

另外，表现较好的侦查蚁将较优位置带入到了寻优蚁群中，是对寻优蚁群的一种扰动，在寻优蚁陷入局部极值的情况下有助于其逃离局部最优。

4.4 算法流程

将提出的动态分级策略、信息素动态加权更新方法、混合重新分级方法代入到蚁群算法中，制定动态分级蚁群算法流程为：

（1）初始化算法参数，包括蚁群规模N、位置维度D、算法最大迭代次数tmax等；

（2）将N只蚂蚁全部放置在起始点；

（3）蚂蚁按照式（1）和式（2）选择下一节点；

（4）当所有蚂蚁到达目标点，将蚂蚁按照适应度值进行分级，迭代次数加1；

（5）侦查蚁和寻优蚁按照各自的选择公式进行路径规划，当完成一次迭代后，按照各自的信息素更新方式进行信息素更新；

（6）将所有蚂蚁混合，按照规划路径的适应度值重新进行分级，迭代次数加1；

（7）判断是否达到最大迭代次数，若是输出最优蚂蚁，算法结束；若否则转至（5）直至算法结束。

5 仿真分析

在前文中从转弯角、避障路径比、路径质量等三个角度对比了蜂巢栅格与方形栅格，证明了蜂巢栅格优于方形栅格，所以本节不再对蜂巢栅格进行验证，而对动态分级蚁群算法从两个方面进行验证：一是迭代过程中蚂蚁的多样性，二是动态分级蚁群算法在蜂巢环境中路径规划性能。

5.1 动态分级蚁群算法多样性验证

为了对比分析动态分级蚁群算法与蚁群算法在迭代过程中的算法多样性，以标准TSPILP库中的KroA100测试集为例进行仿真验证。算法最大迭代次数设置为2000，通过设置程序执行断点，当算法执行至200、500、1000、1500和2000次时统计蚂蚁路径长度的标准差，标准差越大表示蚁群多样性越好，标准差越小表示蚁群越集中，则蚁群多样性越差。路径多样性随迭代次数变化过程，如图4所示。

图4 路径多样性分析Fig.4 Analysis of Path Diversity

从图4中可以看出，在（500～1000）代之间，动态分级蚁群算法的多样性逐渐下降，这是因为经过前期的迭代算法进入以寻优蚁为主导的收敛阶段，使得蚁群向较优路径靠拢，导致蚁群多样性下降。而在（1000～1500）代，动态分级蚁群算法的蚁群多样性逐渐增大，是以侦查蚁为主导的蚁群不断探索开发新路径，导致蚁群多样性提高。从整体上来讲，在整个迭代过程中，动态分级蚁群算法的蚁群多样性优于蚁群算法，说明在蚁群中设置侦查蚁来探索新路径，提高路径多样性是可行而有效的。

5.2 路径规划性能验证

在（40×50）的蜂巢栅格环境中分别使用动态分级蚁群算法和蚁群算法进行路径规划，设置算法最大迭代次数为200，两种算法各独立运行10次进行路径规划，10次规划中最优路径长度随迭代过程的变化曲线，如图5所示。

图5 路径长度迭代过程Fig.5 Path Length Iteration Process

从图5中可以看出，动态分级蚁群算法规划的最优路径长度明显短于蚁群算法，且收敛时的迭代次数也少于蚁群算法。蚁群算法与动态分级蚁群算法规划的最优路径，如图6所示。工作环境中所有障碍物膨胀为圆形，一种栅格为起始栅格，另一种栅格为目标栅格。

图6 最优路径Fig.6 Optimal Path

统计两种算法10次独立寻优的最优值、方差值、平均运行时间和平均收敛次数，如表1所示。

表1 路径规划统计结果Tab.1 Path Planning Statistics Result

从图6和表1可以看出，蚁群算法和动态分级蚁群算法各自独立运行10次，蚁群算法搜索的最优路径长度为59.21，动态分级算法最优路径长度为46.11，路径长度减少了22.12%；且从10次搜索最优路径长度的标准差看，动态分级蚁群算法的搜索稳定性远远优于蚁群算法。从算法的平均运行时间看，动态分级蚁群算法比蚁群算法减少了32.33%，平均迭代次数减少了20.87%。这是因为动态分级蚁群算法根据适应度排序，自适应的将蚂蚁分为寻优蚁和侦察蚁两类，寻优蚁更加注重较优路径的牵引作用，使算法快速搜索；而侦察蚁注重启发信息的引导作用，使算法探索新路径。在信息素更新时，根据不同蚁态和适应度构造信息素更新方法，使信息素兼顾了差异性和普更性，在算法的收敛速度和寻优精度间取得了平衡。

6 结论

研究了机器人在静态环境下的全局路径规划问题，从环境建模和寻优算法两个方面进行了改进。经过验证可以得到以下结论：（1）蜂巢栅格环境下的机器人转弯角、避障路径比和路径质量优于传统的方形栅格；（2）动态分级蚁群算法在迭代过程中的蚁群多样性优于蚁群算法；（3）动态蚁群算法应用于路径规划时，路径规划长度和算法运行时间优于蚁群算法。