大规模柔性作业车间组批调度及求解方法研究

尹 慢，王 爽，张 剑，邹益胜

（西南交通大学先进设计与制造技术研究所，四川 成都 610031）

1 引言

不超过20×50（机床×工件）的车间调度问题为中小规模调度问题[1]，大规模车间调度问题则有以下几种情况[2]：（1）工件数J>50，机器数 M>20 时；（2）当 J≤50，M>20，J×M>1000 时；（3）当 J>50，M≤20，J×M>1000时。不少学者针对作业车间调度问题提出很多求解效果较好的优化方法[3]，但是求解规模通常都是中小规模[4]。大多数优化算法因其求解效率和质量问题，不能直接用于求解大规模调度问题。目前解决大规模调度的方法有：智能优化算法、拉格朗日松弛分解法、基于问题分解法[4]。

各种分解法和智能优化算法首先被应用于规模不断增大的车间调度问题。文献[5]采用拉格朗日分解法，将调度问题的数学模型分解成若干个独立的调度子问题，分别求出各个子问题的解，然后将其解构成原问题的解。文献[6]通过将机器分解为不同的加工单元，降低了求解的难度。文献[7-8]都采用了移动瓶颈机分解的方法，在满足瓶颈工序调度的前提下，非瓶颈工序进行快速调度，从而降低大规模作业车间调度问题的复杂度。文献[9-10]将调度的总时间划分成若干个时间区间，从而将调度问题分解成若干个子问题，每个子问题与一个时间区间对应。这些方法的优点是能较好的表征动态调度问题，对动态大规模调度问题有较好的适应性，但会出现死锁现象。

随着工件数、机器数的增加，JSP问题的求解空间变得复杂，传统的求解算法在解的质量和求解时间上不能满足要求。因此提出基于工件组批调度，将小批量多种类的零件按照其特性进行相似性聚类后再调度。采用基于OBX的自适应遗传算法对每个批次的批量大小进行优化，从而降低调度规模及其复杂性，以获取最优调度结果。经实例验证该方法可以有效地缩减工件完工时间、减少订单拖延期和寻优时间。

2 基于工件特性相似组批方法

该方法首先将加工工艺类似、管径尺寸在同一范围内，且毛坯材质相同的零件进行聚类组批，每个工件都有各自的交付期，组批之后按照本批当中最早交付期进行调度。例如有10件工件，其主要特性，如表1所示。管径有两个尺寸范围（6～12）mm和（14～38）mm，工件的主要工艺采用 A、B、C、D、E、F、G代替，其中E和F可以使用同种机器加工，在工序顺序相同的条件下，同种工序或不同工序均可采用同类型机器的情况都可认为是工艺类似，按照以上组批方法可得组批结果为：第一组（1、5、9），其交付期为2017/07/1；第二组（2、10），其交付期为 2017/07/1；第三组（3、4、6、7、8），其交付期为 2017/07/2。

表1 工件特性表Tab.1 Workpiece Characteristic Table

3 问题描述

所讨论的柔性作业车间调度问题可以详细描述为，在m台设备（上加工 n 件工件（J=｛JlJ1，J2…Jn，l=1，2…n｝），每个工件包含 N 个事先确定加工顺序的工序，每个工序可以在多台设备上加工。组批之后形成r类工件R=第 i类工件的第 j道工序在设备 k 上加工时间为Tijk，Tpi表示第i类工件的第p批次最后一道工序的完工时间，Ds表示工件s的交付期，Dpi表示第i类工件的第p批次的交付期。调度目标是使最大完工时间最小及总拖延期最小。

式（3）表示第i类工件第p批次的第j道工序加工时间等于本批次所有工件加工时间之和。

式（4）同一批次同一个工件的后一道工序的开工时间大于前道工序的完工时间：

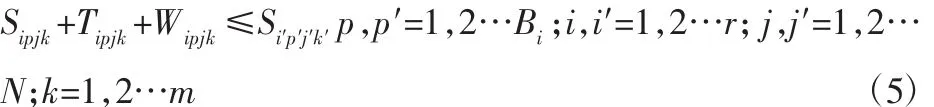
式（5）占用同一台机器，后一个批次工件的开工时间大于前一个批次工件的完工时间。

每类工件所有批次工件数量总和等于所有工件数总和，如式（6）所示。

第i类工件的第p批次的交付期等于本批中最早交付期，如式（7）所示。

具体符号含义，如表2所示。

表2 符号含义Tab.2 Symbolic Meaning

4 基于OBX交叉方式的自适应遗传算法

4.1 编码

为适应大规模柔性作业调度问题而采用三层编码方式。假设有两类工件，每个工件有两道工序，如图1所示。第一层表示工件组批后形成的批次数量，采用整数编码Chrom（1，1）表示第1类工件组成2批。由于基于工序编码的简单并能保证可行解的产生[11]，故第二层采用基于工序的编码方式，表示工件工序的加工顺序，其中101表示第1类工件的第一个批次，102表示第1类工件的第二个批次，101第一次出现在工序基因内表示其第一道工序，依次类推，工序基因表示的加工顺序为101→201→102→101→201→102。第三层采用整数编码，表示工件工序加工所选择的机器，Chrom（1，9）表示工件101的第一道工序在可选机器集Mij内选择第一台机器2。

图1 染色体编码图Fig.1 Chromosome Coding Diagram

4.2 选择

选择算子采用轮盘赌注的方法，因该方法便于操作，故被广泛地运用于选择操作。在此方法中个体被选择的概率和其自身的适应度值相关，适应度值越大被保留下来的概率就越大。

4.3 交叉方式

种群经交叉洗牌后，随机选择两个个体，并截取其工序基因交叉，如图 2（a）所示。采用基于 Order-Based Crossover（OBX）的改进交叉算子，其交叉步骤见图，如图2（a）所示。首先在父代P1中随机选择待交叉基因，形成交叉基因池Pos（201，101，102）。基因Chrom2的第一类工件批次数为1，由于在Chrom2的工序基因中没有 102，故从 Pos（201，101，102）中删除 102，最终用于交叉的基因有Pos（201，101）。然后在父代P2随机选择一个201和101，如图2（b）所示。并删除P2中被选中的基因。最后用P1被选中的基因顺次填补P2中空缺的基因形成子代C2，如图2（c）所示。P1 去除未被选中的基因，剩余 Pos1（102，201，101，102），用P2 中剩余的基因 Pos2（101，202，201，202）并去除 P1 中没有的个体202，依次填补P1中的空缺形成子代C1，如图2（c）所示。

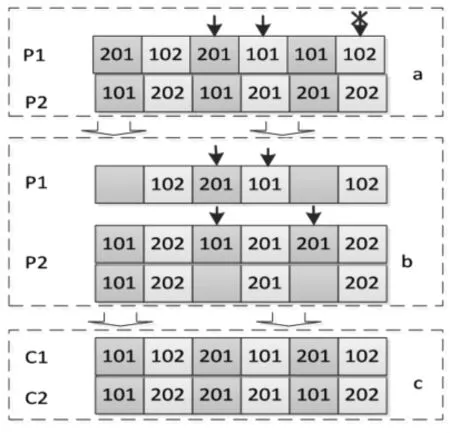
图2 基于OBX的工序交叉流程图Fig.2 Process Cross Flow Chart Based on OBX

染色体交叉长度会影响算法性能，这里研究染色体交叉长度与算法求解精度及运算速度之间的关系。选择染色体长度的10%到100%进行交叉，并各运算10次求其平均值，然后求加权值，得出交叉长度在占染色体长度为10%时最优。为了找出更优的目标值，又选择染色体长度的10%到20%进行交叉进行仿真运算得出选择染色体长度12%进行交叉可以获得更精确的解和提高运算速度，故选择交叉长度为12%。

4.4 变异

变异分为批次变异和机器变异，其中批次变异，如图3（a）所示。每次批次变异后工序基因和机器基因都需要重新解码形成新的染色体，以保证染色体的合法性，如第一类工件批次减少1则工序基因相应的减少一个工件102，而第二类工件的批次增加1则工序基因则增加工件202，两者的机器基因均根据工序基因选择相应的机器。机器变异，如图3（b）所示。如Parent（1，9）变异为2，表示选择M11（2，3）中的3号机器。

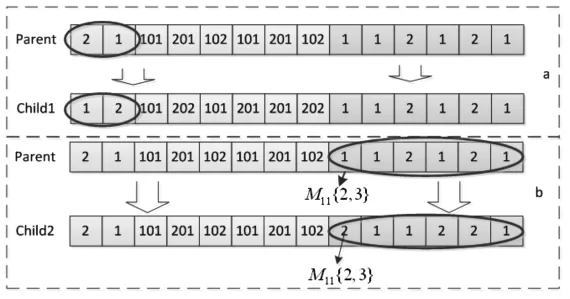
图3 变异流程图Fig.3 Variation Flow Chart

4.5 交叉率及变异率正弦自适应

正弦自适应是交叉率及比变异率根据个体平均适应度值以及最大适应度值按照线性函数曲线变化的一种自适应方法[12]。在优化过程的初始阶段选取较大的交叉率和变异率可以获得较快的收敛速度且保持种群的多样性，经多次迭代后，为避免最优解被破坏，此时选取较小的交叉率和变异率进行细致搜索，经实验验证，正弦自适应遗传算法可以提高算法的收敛速度及收敛精度，并且利用此方法可以保证算法搜索的全局性和精确性。

5 实例验证

某工厂生产导管类零件，抽取其中的典型零件进行实验，每个工件有4道工序且有各自的交付期，每个工件的加工时间及加工准备时间由厂方提供（单位：分钟），初始参数设置：交叉率0.1，变异率0.04，种群规模40，迭代终止条件300代。

实验设计为四种规模，分别为 230×18、460×18、690×18 及1150×18（工件数量×机器数量），按照上述组批方法，将零件随机组成不同的批次，然后采用基于OBX交叉方式的自适应遗传算法优化。设计4组实验进行对比，在相同的运行环境下每组实验各运行10次，并取其平均值进行对比。运行结果，如表3所示。

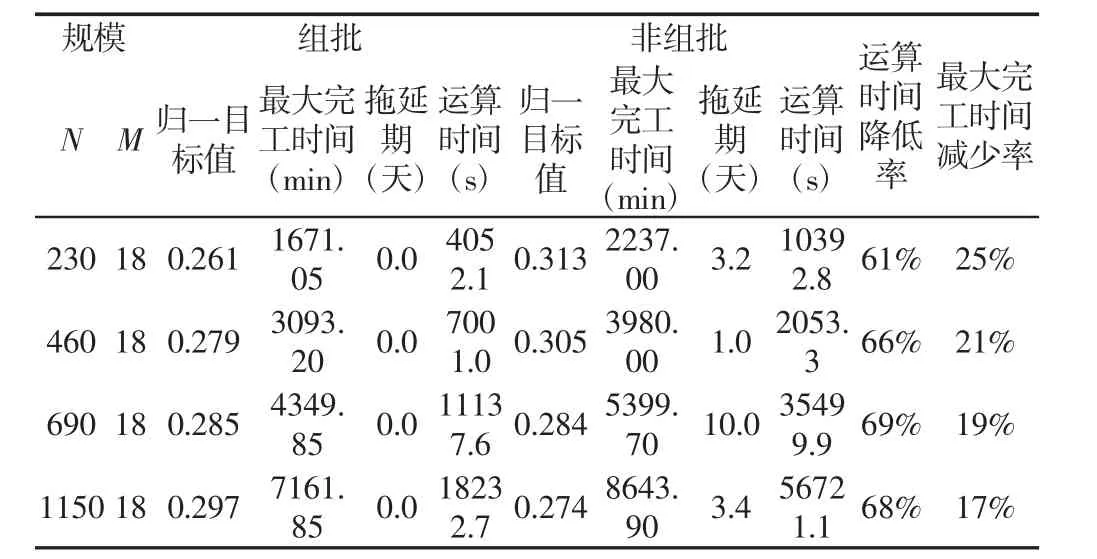
表3 实验结果数据表Tab.3 Data Table of Experimental Results

由表3可知，四种不同大规模的JSP问题经过组批调度之后拖延期均为0，而非组批调度方法均有不同程度的拖延；最大完工时间至少缩减17%，最多缩减25%；运算效率至少提高61%，最大提高69%。

6 结论

大规模柔性作业车间问题随着工件数、机器数的增加，求解空间变得复杂，传统的求解算法在解的质量和求解时间上不能满足要求。针对此问题提出基于工件组批调度，采用基于OBX的自适应遗传算法对每个批次的批量大小及加工顺序进行优化，从而降低调度规模及其复杂性，减小完工时间，无拖延期，大幅度提高了优化求解效率。