助力下肢外骨骼直立行走过程研究

许鸿谦，刘 放，南婧雯，朱 粤

（西南交通大学机械工程学院，四川 成都 610031）

1 引言

助力下肢外骨骼是一种与人体下肢相似的机械装置，它将人体下肢包裹或与人体下肢并联。通过复杂的控制系统控制处于各关节角处的各执行机构，使其从动于人体运动，增加人体的负重能力及单兵作战能力[1]。不同于传统意义上的机器人，机器人在复杂状况下的处理能力尚不能达到需求，而下肢外骨骼可以将人本身的优势与其结合，“以人为主，机器为辅”能达到更好的性能[2]。

国外对助力下肢外骨骼研究较早，可分成如下阶段：（1）文献[3]为解决通用的负载运输平台进行研究，建立了BLEEX系统，实验状态下能在跑步机上以1.3m/s的速度动作。文献[4]采用基于关联矩阵的边缘图，对下肢外骨骼的关节速度进行分析研究。（2）文献[5]应用重量支持的理念对减轻下肢外骨骼膝关节压缩负荷进行研究，建立了knee-joint模型，分析了顺从耦合和体重支持。文献[6]采用摆动模式的动态识别系统对下肢外骨骼的行走过程进行分析研究，建立动力学模型。（3）文献[7]采用了四项核心技术为实现BLEEX在负重34kg以1.3m/s行走进行研究，分析了测量系统的鲁棒性。文献[8]采用除噪点的EMG-Based神经模糊控制方法对下肢外骨骼的控制问题进行研究，通过比对EMG信号和关节力矩的关系印证了该方法的有效性。

国内学者也对助力下肢外骨骼进行了相关研究。文献[9]研究可穿戴式下肢助力机器人的运动学，建立运动模型并仿真验证可行性。文献[10]研究下肢外骨骼特殊步行工况下的动力学问题，对行走模型进行优化。文献[11]研究人体踝关节运动力学，设计并建模仿真了主、被动结合的低功耗假肢。

助力下肢外骨骼在行走过程中不同的工况下的动力学模型各不相同。为动力驱动方式、动力系统以及控制系统提供理论研究基础，以西南交通大学研发的第二代助力下肢外骨骼样机为研究对象，以人体直立行走运动规律为基础，建立在所选工况下的行走过程的运动学模型，基于MATLAB平台进行仿真计算，根据结果分析助力下肢外骨骼各关节角的运动学特性，并计算驱动液压缸的线速度及线加速度，为液压缸选型作参考。

2 人体行走动作运动学分析

2.1 实验背景

人体是一个复杂的系统，从整体来看，人体结构可分为头部、颈部、躯干、四肢（上肢、下肢）等部分。其中，下肢包括脚、小腿和大腿；上肢包括手、前臂和上臂。本次实验对行走过程进行研究，主要研究下肢及躯干对系统的影响。

实验选取年轻成年男性作为实验对象，在不同速度（3km/h、4km/h、6km/h）不同负重（0kg、10kg、30kg）的条件下进行人体行走过程实验数据的采集。通过光学捕捉系统和高速摄像机获取头、肩、胸、髋、膝及踝等测试点的三维坐标值，其采样频率为200Hz。

2.2 人体行走模型简化及特征分析

实验研究发现，人体行走主要是在矢状面内的运动轨迹，在额状面和水平面的运动较小，简化模型忽略其影响。为方便研究，将下肢外骨骼机器人简化成球棍图模型，如图1所示。H、S、P、K、A、HE、T分别为头、肩、髋、膝、踝、脚后跟、脚趾。初始状态是人体呈站立状，左脚向前跨步（以左脚先跨步为例），同时人体重心前移，左脚落地后作为支撑脚，右脚再向前跨步，依次循环，基于运动生物学步态划分RLA法，将人体行走动作划分为支撑周期和摆动周期，如图2所示。

图1 人体行走简化模型Fig.1 Human Walking Motion Simplified Model

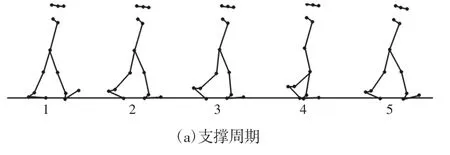
图2 人体行走动作棍图Fig.1 Human Walking Motion Stick Diagram

其中：1-2初始着地期；2-3支撑反应期；3-4中点支撑期；4-5支撑后期；5-6摆动前期（推离期）；6-7摆动早期；7-8摆动中期；8-1′摆动后期

2.3 人体行走动作特征建模

特征角分别为躯干与左右大腿的夹角α1、α2，左大腿与左小腿夹角θ1，右大腿与右小腿夹角θ2，左小腿与左脚尖夹角β1，右小腿与右脚尖夹角β2，如图1所示。人体行走在单一周期内的左右腿极为相似，只需选取单侧进行研究，以左侧为例。

以计算髋关节α1为例，在ΔS1P1K1中：

利用余弦定理可得 α1，同理可得 θ1、β1：

获得各关节角之后需要对其进行曲线拟合，通过对人体行走动作时关节角的分析可知，在人体行走动作时，特征角都呈非线性变化。其变化规律有较强的规律性，对数据分析后采用非线性数据拟合法对离散数据进行曲线拟合。采用高斯拟合函数进行曲线拟合。经过对比和分析，各关节角采用8阶高斯函数作为基函数进行曲线拟合，如式（4）所示。

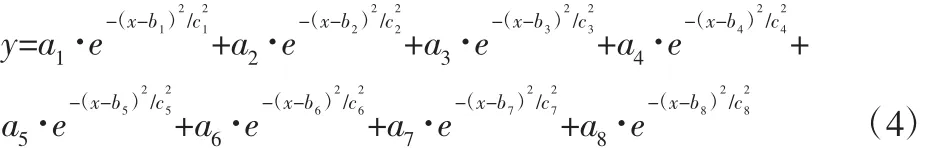
3 下肢在不同工况下的对比分析

3.1 负重相同，行走速度不同

人体负重0kg，分别以3、4、6km/h的速度直立行走时，髋关节、膝关节、踝关节的左右腿的关节角，如图3所示。其中1为左腿，2为右腿。通过光学捕捉系统，测试者在直立行走过程中，每个特征点获得约400组有效数据，频率为200Hz。各行走速度的耗时不同，最大不超过2.5s。直立行走动作是一种周期性的动作，各关节角的角度变化呈现周期性，如图3所示。由图可知，在负重0kg时，随行走速度增快，左右髋、膝、踝关节的动作周期越短；左右髋关节角基本不变，速度对关节角的影响较小；左右膝关节角减小，幅度减小；左踝关节角先基本不变后增大，右踝关节角先基本不变后减小，幅度增大。

图3 负重0kg行走动作特征角Fig.3 0kg Weight Walking Motion Joints Angle

3.2 速度相同，负重不同

人体以 3km/h，负重 0、10、30kg，髋、膝、踝关节的左右腿的关节角，如图4所示。其中1为左腿，2为右腿。

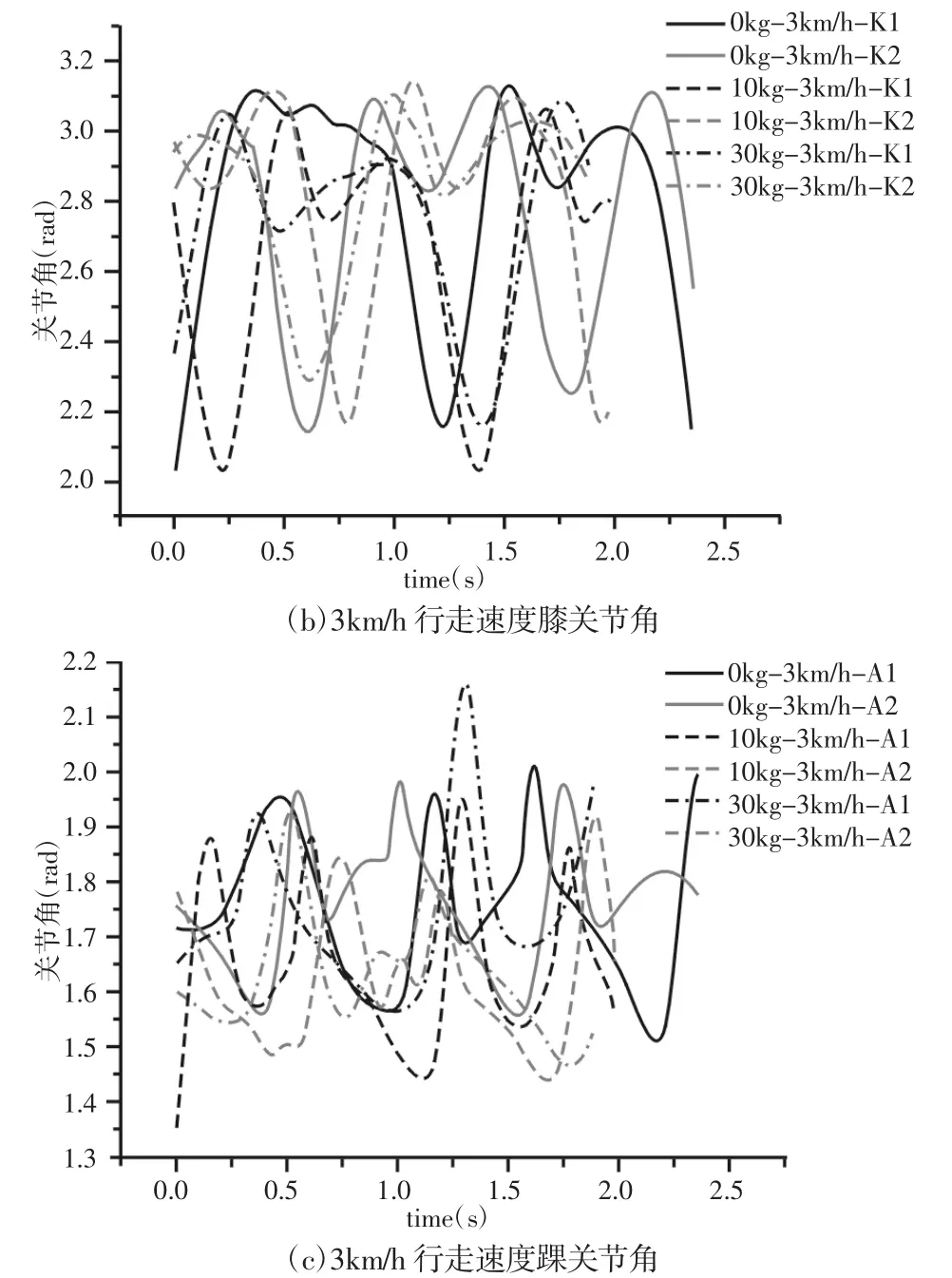
图4 速度3km/h行走动作特征角Fig.4 Speed 3km/h Walking Motion Joints Angle

在测试过程中，实验人员以3km/h的速度直立行走，不同负重下特征点的有效数据点数量不同。由图可知，在以3km/h速度行走时，随负重的增加，左右髋、膝、踝关节的时间差基本不变，约6s；左右髋、膝、踝关节的周期变长，行走动作变慢；左髋关节角变小，右髋关节角先增大然后减小，但总的髋关节角变小，人体背部呈现不均匀前倾；左右膝关节角先减小后增大；左右膝的幅度呈现减小趋势；左右踝关节角呈现减小趋势；左踝的幅度增大，右踝幅度先增大后减小。

4 外骨骼行走过程液压缸动力学分析

外骨骼样机是由左右腿液压缸提供动力的，将其简化成棍图，如图5所示。

图5 下肢外骨骼液压缸Fig.5 Lower Extremity Exoskeleton Hydraulic Cylinder

其中，膝关节角θ1为式（4）。经测量 L1=85mm，L2=360mm。采用余弦定理可得液压缸长度L3，进行一、二阶求导可得液压缸线速度v及线加速度a，如式（5）、式（6）所示。

下肢助力外骨骼负重0kg分别以3、4、6km/h速度行走，液压缸的线速度、线加速度曲线，如图6、图7所示。

通过对上述工况分析，下肢外骨骼负重相同时，随行走速度的增大，液压缸的线速度增大，变化幅度增大；左右液压缸的线速度在低速时相差不大，在高速时左腿更快，幅度更大；线加速度增大，周期变短；左液压缸比右液压缸线加速度更大。外骨骼以6km/h行走时液压缸最大有效线速度为414mm/s，最大有效线加速度为8190mm/s2。

图6 液压缸线速度曲线Fig.6 Linear Velocity of Hydraulic Cylinder

图7 液压缸线加速度曲线Fig.7 Linear Accelerated Velocity of Hydraulic Cylinder

5 结论

以西南交通大学第二代助力下肢外骨骼样机作为实验研究对象，对人体在不同速度、不同负重的各种工况特征数据分析，拟合获得人体各关节角方程。以MATLAB为平台对负重0kg时不同行走速度、行走速度3km/h时不同负重进行数值计算及分析，并以负重0kg为例计算下肢外骨骼膝关节处液压缸的线速度及线加速度，得出以下结论：

（1）在负重0kg时，人体行走速度越快，髋、膝、踝关节的运动周期越短；随行走速度的增加，左右髋关节角基本不变，速度对髋关节角的影响较小；左右膝关节角减小，幅度减小；左踝关节角先基本不变后增大，右踝关节角先基本不变后减小，幅度增大。

（2）人体行走速度为3km/h时，随负重增加，踝、髋、膝关节角动作周期变长，人体行走动作变慢；左髋关节角减小，右髋关节角先增大然后减小，但总的髋关节角变小，人体背部呈现不均匀前倾；膝关节角幅度减小，踝关节角减小。

（3）下肢外骨骼。随行走速度的增大，液压缸的线速度增大，变化幅度增大；左右液压缸的线速度在低速时相差不大，在高速时左腿更快，幅度更大。