基于非均匀消除-扩散概率分布的情绪化细菌觅食算法

董 海，齐新娜

（1.沈阳大学应用技术学院，沈阳 110044；2.沈阳大学机械工程学院，沈阳 110044）

（∗通信作者电子邮箱1205344726@qq.com）

0 引言

自20 世纪40 年代以来，针对工程存在的具有高维度、多峰值、非线性且不可微分等特征的实际问题，许多仿生优化演进算法被广泛用于优化多式联运、单一方式、多变量、多层面、多目标工程问题的基准功能［1］。初始阶段应用较广泛的搜索最优解的优化技术是Mirjalili［2］提出的遗传算法（Genetic Algorithm，GA），GA 是通过模拟自然进化过程搜索最优解的方法，该算法被广泛应用于解决许多复杂的最优解和满意解等现实问题。Eberhart 等［3］开发了粒子群优化（Particle Swarm Optimization，PSO）算法，该算法拥有更好的收敛性和更精确的优化效果，但网络权重编码的选择较麻烦，计算成本高。刘晓阳等［4］提出了蚁群优化（Ant Colony Optimization，ACO）算法，该算法是用来在图中寻找优化路径的几率型算法，适用于图上路径搜索问题。李晓磊等［5］提出鱼群优化（Fish Swarm Optimization，FSA）多用于精度要求不高的情况，可快速得到一个可行解，具有局限性。继Müller 等［6］提出的基于单个细菌运动行为的细菌趋药性（Bacterial Chemotaxis，BC）算法之后，Passion［7］在2002 年提出细菌觅食优化算法（Bacterial Foraging Optimization Algorithm，BFOA），研究表明：尽管BFOA的搜索性能优于GA，但不及GA成熟。

为了提高BFOA 的性能，一些学者从算法融合和算法参数上进行了研究。在算法融合方面：刘小龙等［1］将分布估计算法的思想引入BFOA 的繁殖过程，提出了基于高斯分布估计的细菌觅食算法；刘小龙等［8］将免疫算法与BFOA 进行融合，提出了基于免疫算法的细菌觅食优化算法；王振东等［9］将混沌优化算法融入BFOA，提出了混沌优化细菌觅食算法；徐玉韬等［10］将差分进化算法中的交叉与变异操作引入BFOA，提出了一种混合型全局优化算法。在算法参数调整方面：易军等［11］提出了基于变邻域趋化操作的BFOA，利用邻域搜索提高局部最优解的精确度；章国勇等［12］提出了一种具有量子行为的细菌觅食算法，以细菌群体信息为依据建立量子化的势能阱模型；谢平平等［13］提出了基于社会学习自适应BFOA，将社会学习机制及自适应步长策略引入到标准BFOA 中进行算法改进；蔡昌春等［14］提出了基于神经网络改进的细菌觅食算法；王新刚等［15］对趋化操作的运动步长以及翻转方向进行了改进，提出了一种改进型细菌觅食算法。

综上所述，上述研究提出的改进型BFOA，其自适应趋化步长存在不适用于多模情况等局限性，且忽略了消除-扩散过程中概率的非均匀性［16］。针对上述问题，本文将基于情绪智能的突变引入标准的BFOA，并结合符合非均匀概率分布的消除-扩散操作，提出了一种基于非均匀消除-扩散概率分布的情绪化细菌觅食算法，通过仿真及算法对比，验证了算法具有良好的优化性能。

1 算法设计

标准的细菌觅食优化算法（BFOA）通过趋化、群集、繁殖和消除-扩散四个步骤进行优化。在BFOA 中，通过游动和翻转进行优化。在游动的过程中，如果细菌获取到最佳状态，会朝最佳状态食物功能评估，并改变其在最大食物方向上的位置。

首先，在任何优化技术中，最优解的精度和收敛性都取决于步长。由于BFOA的步长尺寸固定［17］，存在以下缺点：

1）如果步长尺寸较小，可能无法获取到全局最优值；

2）如果步长尺寸较大，有可能在局部极小处捕获细菌，虽可快速获得最优解，但最优解的精度不高；

3）如果步长固定，细菌在接近最佳值时振荡，无法收敛于最佳值。

针对上述步长存在的不确定性，本文利用自适应或动态的步长来修正BFOA，以获得低计算成本的最优解；与此同时，为了减少计算时间，提高经典BFOA 中最优解的精度，本文拟从以下三个方面对BFOA 进行改进。首先，对其位置进行更新，在趋化步骤中提出古斯分布搜索机制；其次，对其步长大小进行改进，在初始阶段，固定的步长用于局部搜索，当生成的数量增加时，利用自适应或动态步长进行全局搜索，并利用情绪智能的突变来实现自适应步长；第三，标准的BFOA在消除-扩散过程中，所有细菌个体都服从恒定的消除-扩散概率，这项操作会使即将接近最优位置的细菌替换为远离最优解的细菌，从而影响其收敛速度，本文利用线性和非线性概率分布代替传统的常数分布来实现非均匀分布。具体算法设计如下。

1.1 改进的趋化操作

传统的BFOA 由于趋化操作，其搜索性能较差，发现每一种细菌都通过随机翻滚来调整自己的游动和翻转方向，使每一种细菌都能在特定的环境中生存。在整个生命周期内，以随机方式在每个维度上游动或翻转，从而使细菌具有较差的搜索能力，如果整个搜索空间很大，则容易陷入局部最优。此外，每个细菌的运动都是孤立的，在趋化操作中缺乏信息交换能力。为了解决细菌运动的基本趋向步骤，本文提出了基于古斯分布的搜索机制，对趋化性细菌的运动规律进行调整［17］。假设细菌i的位置由θi(j，k，l)表示，其中：j为趋化步骤，k为繁殖步骤，l为消除-扩散步骤。C（i）表示每次游动或翻转的趋化步长大小，那么对于每次趋化步骤，细菌i的运动可表示为：

否则：

其中：

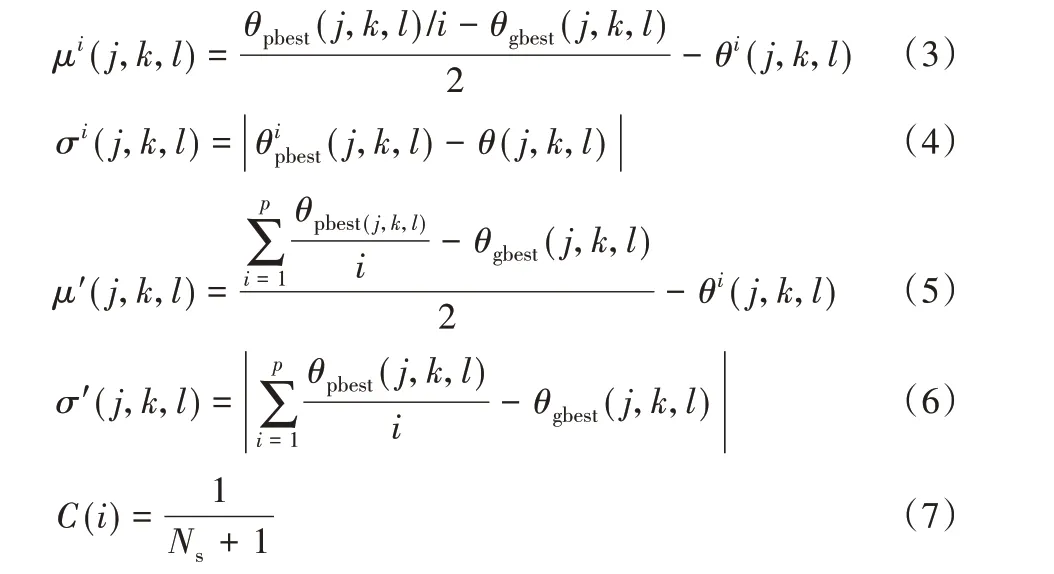
式中：N表示游动或翻转的次数；p表示局部细菌个体总数。

1.2 群集操作

接近最优路径的细菌个体可跟随其他较低梯度的细菌个体进行觅食，以便更快地收敛。菌群的群集行为使细菌个体形成群体，并以同心圆为轨迹进行运动，菌群密度高，则食物梯度高。该群集机制可建模型，如式（8）表示。

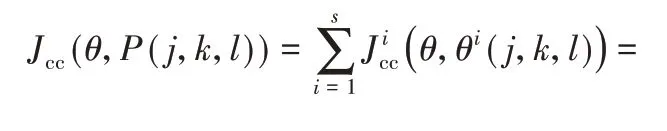
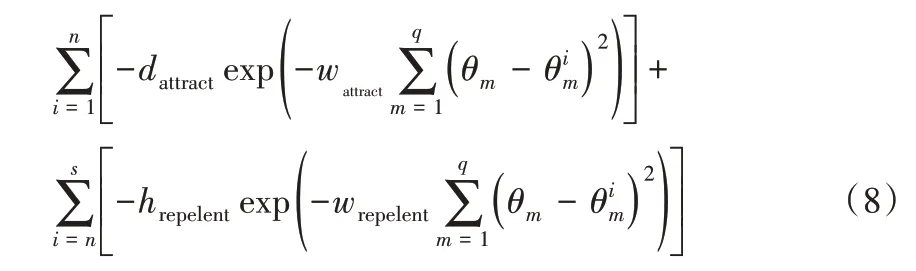
其中：Jcc(θ，P(j，k，l))表示细菌个体之间的吸引和排斥作用值；θ∈{θ1，θ2，…，θq}表示q维搜索域中的一个点；s表示细菌的总数；q表示优化变量的个数；n表示维度内某节点；dattract、wattract分别表示细菌的引诱因子深度和宽度的度量系数；hrepelent、wrepelent分别表示细菌驱避高度和宽度系数。

1.3 情绪化突变

基于情绪智能突变使细菌的位置发生动态变化，在基于非均匀消除-扩散概率分布的情绪化细菌觅食算法中，突变发生在繁殖步骤之前。在突变中，采用自适应步长可避免过早收敛，此过程假设细菌有心理，每种细菌都有两种情绪：快乐和悲伤，每种细菌都会根据自己的感受对当前的位置作出反应，不同的位置被用来刺激下一代的细菌。利用著名的韦伯-费克纳定律计算情绪感知因子。由韦伯-费克纳定律描述的刺激强度P大小之间的关系［16］，如式（9）所示：

其中：k为常数因子；S0为刺激阈值；S为刺激函数。刺激和感知之间使用对数关系。如果一个刺激依据几何表达式变化，并且相应的知觉在对数关系的数学表达式中改变。细菌的全局感知rg和历史感知rh分别通过方程式（10）～（11）来描述：

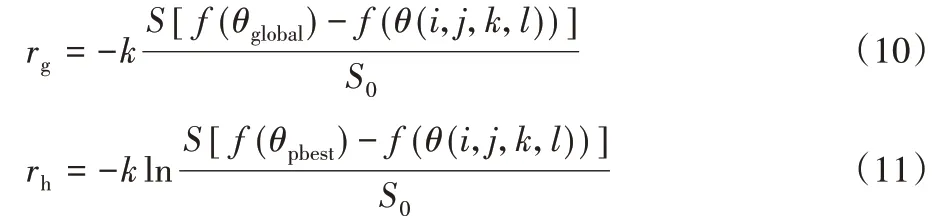
其中，f(θ(i，j，k，l))表示如果细菌远离全局最佳位置，将对刺激产生强烈的反应，这些刺激将与其所经历的历史相比较。细菌的快乐和悲伤两种情绪会动态地改变细菌的位置，使其步幅变小或变大，细菌的情绪表现如方程式（12）～（13）所示。

快乐的细菌个体为：

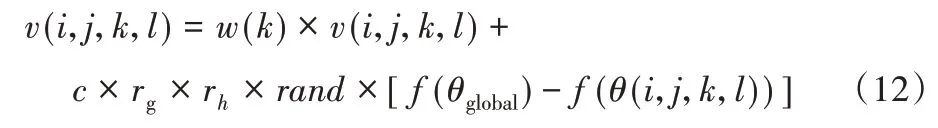
悲伤的细菌个体为：

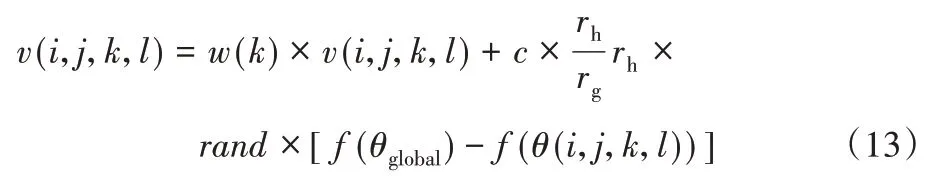
其中：θglobal表示全局最佳位置；f（θglobal）表示全局最佳位置适应度；f（θ（i，j，k，l））表示实时的适应度；v（i，j，k，l）表示细菌速度；w（k）表示线性减小惯性重量；c表示加速度系数；rand表示随机函数。

根据情绪感知因子更新细菌速度：如果随机函数rand小于情绪感知因子es，依据式（12）更新细菌速度；否则，依据等式（13）更新细菌速度。

根据式（14）可推断出全局最佳位置υ(i，j+1，k，l)，以更新每种细菌的当前位置：

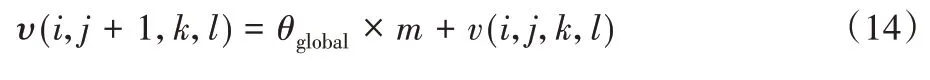
其中，m表示动力因子。

为了防止细菌在游泳或翻转后离开脱水区域，使用动量因子。动量因子限制了未定义的搜索空间中的细菌，因此不必在每一代之后检查细菌的位置，从而节省计算成本。动量因子的选择为随机值而不是常量值，因为所有细菌每次都会被拉入具有不同限制的搜索空间，从而导致无法逃离全局最优值。在整个搜索空间，搜索实验的初始阶段步长非常大，当细菌接近全局最优值时，步长会动态地缩减，因此，自适应步长f（θ（i，j，k，l））将更接近f（θglobal）。

1.4 繁殖操作

在基于非均匀消除-扩散概率的分布的细菌觅食算法中，细菌的繁殖类似于经典的BFOA，随着营养素的不断吸收，细菌逐渐生长。在适当的条件下，每个健康的个体会分裂成两个子细菌，但是，对于营养不良的个体这些细菌会被清除。为了保留细菌趋化过程中的良好经验，加快算法的收敛速度，本文将细菌适应度在历次趋化过程中的历史最优值作为健康适应度函数Jhealth［13］，再现操作排序如式（15）所示：

其中，Nc为趋向步骤次数。

1.5 非均匀概率分布的消除-扩散操作

为了避免在局部最优条件下存储细菌的可能性，提高细菌的搜索能力，一些细菌被消除，而一些则根据概率分散在搜索空间中内，即在该过程中，具有最佳适应度值和最差适应度值的细菌均以相同概率被消除。因此，会将接近最优位置的细菌个体替换为远离最优位置的细菌个体，从而影响算法的性能［16］。据此，本文提出依据非均匀概率分布消除细菌，该方法是通过将细菌重新定位到环境中的随机位置来实现该过程的。线性消除概率定义为：

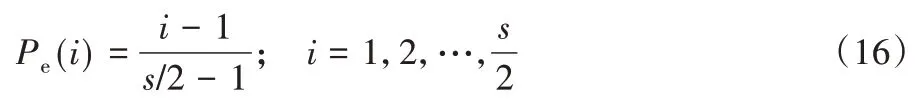
根据式（16）可知，种群内的消除-扩散概率与种群内的细菌指数成线性正比，其概率步长增加为s/2，在该情况下，获得最佳适应度的细菌被消灭的可能性最低，适应度最差的个体因被分配了等同的概率而被淘汰。另一种非均匀分布概率可用于定义非线性行为，如式（17）所示。

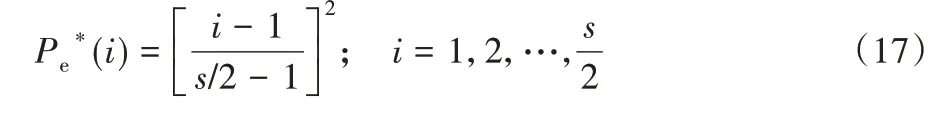
在该概率分布中，最优细菌个体将具有最低的概率，而最差的细菌个体将完全被淘汰，在这种情况下概率与细菌指数成线性正比。

消除-扩散概率（Pe）决定了搜索过程中的探索和开发的量：Pe值越大，消除作用越强，对细菌的迁移作用越好，可避免陷入局部极小值，并且探索过程越容易实现；Pe值越小，越可保证最佳细菌的发展，并可加强对局部区域的研究，然而这种细菌将有更少的机会被从局部区域释放，可能会造成局部极小值。因此，控制Pe值至关重要。在研究初期本文采取探索整个搜索空间，相反，在搜索结束时进行开发（增强），该操作可通过分配小的Pe值来实现。对于线性分布及非线性分布可推广为包含消除-扩散指数，分别定义如式（18）、（19）所示：

线性为：

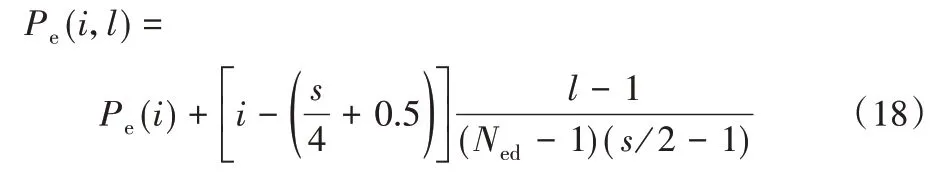
非线性为：

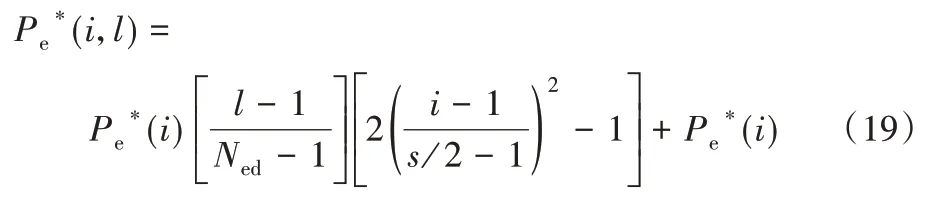
1.6 算法设计

本文提出的基于非均匀消除-扩散概率的情绪化细菌觅食算法流程如图1所示。

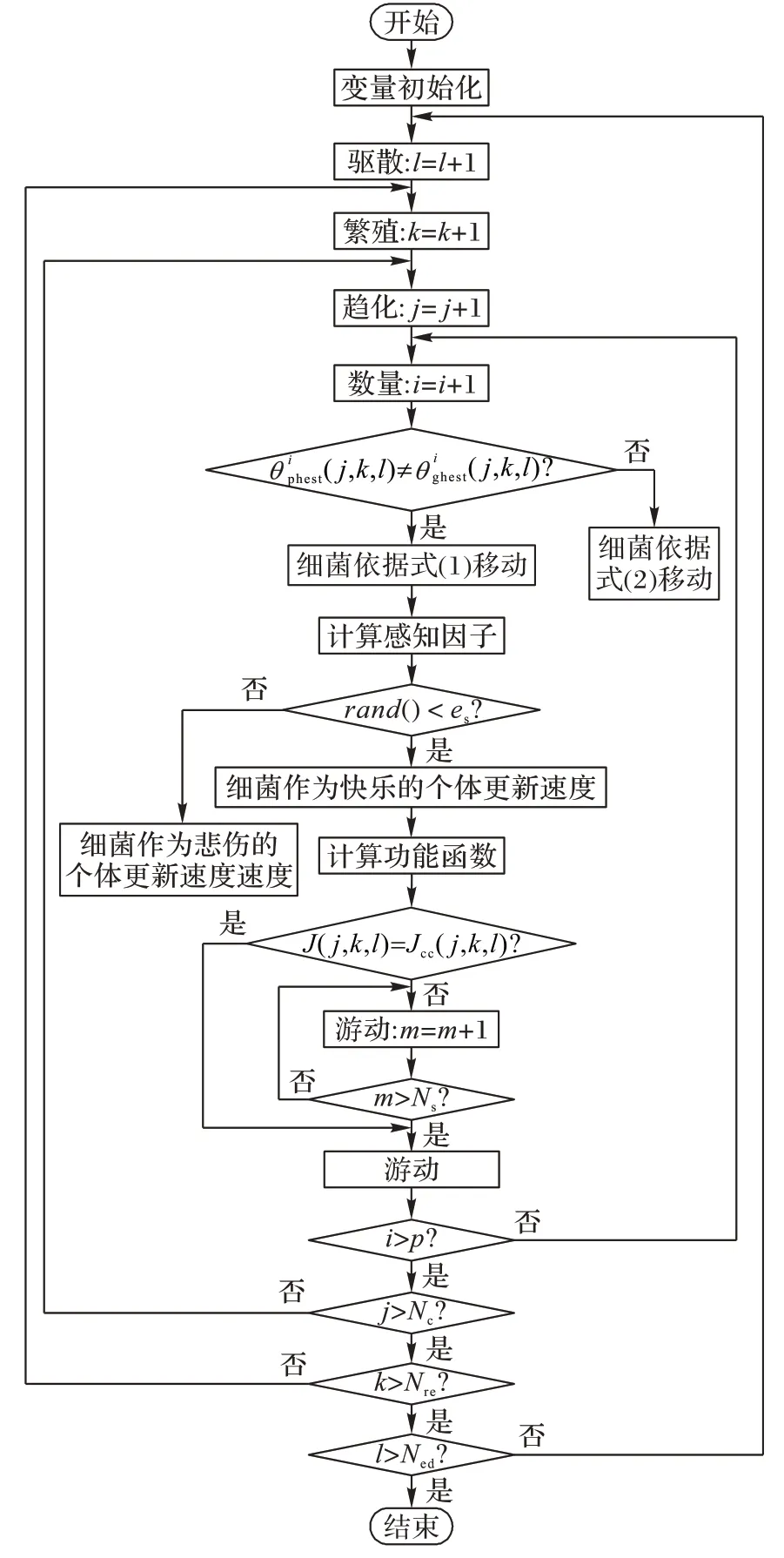
图1 本文算法流程Fig.1 Flowchart of proposed algorithm

2 仿真实验与结果分析

2.1 仿真设计

表1 给出Rosenbrock、Sphere、Griewank、Schaffer’s、Shekel’s Foxholes、Rastrigin六个基准函数，测试本文提出的基于非均匀消除-扩散概率分布的情绪化细菌觅食算法，并验证算法的性能。其中：f1（x）与f2（x）为单峰函数，解的空间有非常多狭窄的局部极小通道；f3（x）、f4（x）、f5（x）与f6（x）为多峰函数，算法很容易陷入通向全局最优点的局部最优上。表2为全局最优搜索范围及初始化范围的参数，表中d表示无限大。表3为算法参数设置。

表1 模拟基准函数Tab.1 Simulated benchmark functions

表2 搜索范围及初始化范围Tab.2 Search range and initialization range

2.2 算法对比分析

为测试新算法的性能，本文对具有量子行为的细菌觅食算法（Bacterial Foraging Algorithm with Quantum Behavior，BFAQB）、差分进化改善的细菌觅食算法（Improved Bacterial Foraging Algorithm Based on Differential Evolution，IBFABDE）、基于高斯分布的细菌觅食算法（Bacterial Foraging Algorithm Based on Gaussian Distribution，BFABGD）及本文提出的基于非均匀消除-扩散概率分布的情绪化细菌觅食算法（Nonuniform Probability Emotional Bacteria Foraging Algorithm，NPEBFA）在上述六个基准函数进行测试，实验对比结果如表4所示。

表4 中，NPEBFA 的性能优于BFAQB 和IBFABDE，但对Rosenbrock 函数的性能不如BFABGD。与NPEBFA 相比，BFABGD 获得的Rosenbrock 函数的平均迭代效率优于NPEBFA。

Sphere 函数的模拟结果显示，NPEBFA 和比较算法执行于球体函数上，标准差分析结果表明，球面函数拟合度的参数值彼此接近。

表3 算法参数设置Tab.3 Algorithm parameter setting

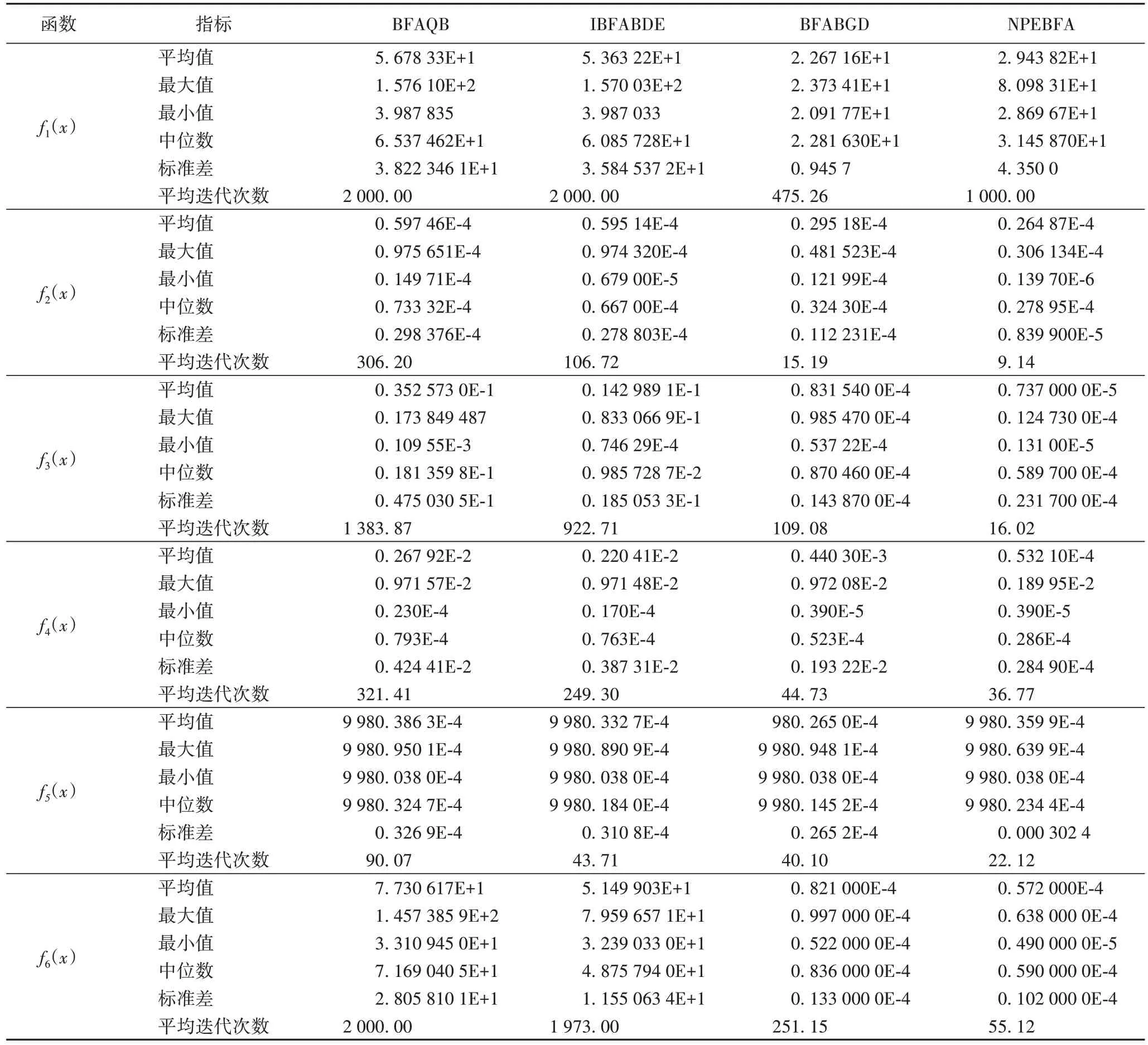
表4 不同算法函数仿真结果对比Tab.3 Comparison of functional simulation results of different algorithms

Griewank 函数的模拟结果显示，该方法可以提高算法的精度和收敛性，通过分析NPEBFA 计算结果，证明其能够以较低的计算成本获得精确的最优解。

Schaffer’s 函数的模拟结果显示，NPEBFA 以较低的计算成本提供了较好的优化质量。

Shekel’s Foxholes函数的模拟结果显示，其全局最小值不是零。对于这种函数，NPEBFA 技术在节省计算成本方面的性能也很好，同时与其他方法相比，拟合参数彼此接近。

Rastrigin函数的模拟结果显示，NPEBFA以最小的计算成本获得精确的最优值。与BFAQB、IBFABDE 和BFABGD 相比，NPEBFA对Rastrigin函数的代数要求较少。

对单个最优函数和多个局部最优函数的实验结果表明，该算法除针对Rosenbrock 函数外，在计算成本较低的情况下，具有较好的优化质量，且对于求解多模态函数等复杂问题更为有效，优化精度高。

不同算法收敛性的比较如图2 所示，仿真结果表明本文提出的NPEBFA 在最优均值范围不同的情况下均具有较好的收敛性，即该算法较BFABGD、IBFABDE、BFAQB 更适用于不同的搜索空间范围，该优势可确保算法优化过程中种群的多样性，并避免范围内待优化因子的丢失。

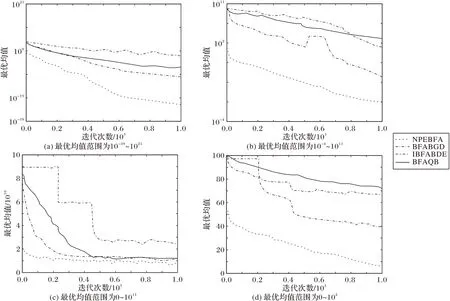
图2 不同算法收敛性比较Fig.2 Convergence comparison of different algorithms

3 结语

本文通过赋予细菌个体情绪感知因子的概念来改变细菌的趋化步长，并将古斯分布搜索机制嵌入趋化步骤中，同时在个体消除-扩散过程中，利用线性和非线性概率分布代替传统的常数分布来实现非均匀分布，进而提出了一种改进的细菌觅食优化算法，算法中的待优化变量的搜索空间在开发能力和探索能力上取得提升。仿真实验结果表明，本文提出的NPEBFA 的性能及收敛性优于传统的BFO 算法，并且避免了其他改进细菌觅食算法存在的部分缺陷，适用于解决高维度工程优化问题。