基于线特征及迭代最近点算法的地基建筑物点云自动配准方法

徐景中，王佳荣

（武汉大学遥感信息工程学院，武汉 430079）

（∗通信作者电子邮箱jz_xu@whu.edu.cn）

0 引言

由于扫描视角的限制，利用地基激光扫描设备进行地物目标三维点云采集时，通常需要设置多个测站才能获取到完整的目标点云。由于不同视角采集到的点云并不在同一个坐标系下，通常需要将点云旋转、平移到统一的坐标系，才能得到完整的地物数据，因此需要进行点云配准处理。

点云配准方法目前主要包括：人工配准方法和自动配准方法。虽然人工方法通过人为选取同名特征进行匹配，能可靠地得到配准结果，但精度有限，且耗时耗力；因此，近年来越来越多的学者开始研究自动配准方法。考虑到点云与点云之间缺乏严格意义的同名点，点云自动配准方法又可以分为基于迭代最近点（Iterative Closest Point，ICP）算法的点云配准方法［1］以及基于特征的点云配准方法［2-3］。前者是利用数学方法迭代寻找两组点集之间的最小距离作为最佳位置，点对的匹配度高，但其存在对初始点云的位置条件要求苛刻、易陷入局部最优等不足。对此，部分学者从配准效率入手进行ICP 算法的改进，如：杨帆等［4］在ICP 算法中引入kd-tree 来提高最近点的搜索速度，而周春艳等［5］采用主成分分析（Principal Component Analysis，PCA）变换，Du 等［6］采用仿射法等方法，这些研究也只是解决了部分问题，仍存在配准完成度低的问题。而基于特征的点云配准方法则是从点云中提取点特征、线特征或面特征，然后通过特征匹配完成点云配准。如：沈长江等［7］、赵明富等［8］直接从点云中提取快速点特征直方图（Fast Point Feature Histogram，FPFH），然后基于FPFH 特征相对关系进行点云配准；但此类基于点特征的配准通常存在受噪声影响较大、时间复杂度较高等问题，因此，部分学者通过构建点的域拓扑信息来提取几何特征，然后基于域特征优化点云配准过程［9］，在一定程度上改善了对噪声的敏感性，但仍存在鲁棒性低的问题。Aiger 等［10］基于共面四点对的仿射不变性，实现了四点全等集合（4-Points Congruent Sets，4PCS）点云配准方法，该方法不需要计算复杂的几何特征，效率较高；但对于点云重叠率较低的情况，算法耗时长且配准容易失败。相较于点特征，线特征几何拓扑稳定性更高，配准结果也更加可靠。Jaw 等［11］提出了一种基于三维直线特征的地面激光雷达点云配准方法，该方法包括三个主要步骤：基于平面拟合相交的三维直线特征提取、基于直线夹角的相似性匹配和基于四元数的多站激光点云配准。王永波等［12］通过平面相交得到线特征并将其作为激光点云配准的基元，利用线特征约束的四元数法构建参数解算模型。此类方法可以快速实现点云配准，但由于提取的线特征的完整性和精确性是有限的，配准结果精度仍需提高。由于面特征包含的信息多于点、线特征，面特征配准方法受噪声影响较小，部分学者使用最小二乘法、随机样本一致性算法［13］和主成分分析方法［14］等曲面拟合方法进行特征面提取，以提高配准精度；但此类方法，要求两组数据重叠区域必须包含许多面特征，否则很难保证配准的准确性。

基于上述分析，本文提出了一种基于线特征及ICP 算法的建筑物点云自动配准方法，该方法包括基于线特征的点云粗匹配以及基于ICP 的点云精匹配过程。该方法利用线对作为配准基元，以线对夹角和距离作为相似性测度，可以提高配准结果的可靠性；此外，采用由粗到精的配准策略，不仅能改善ICP 算法易陷入局部最优的不足，同时可以保证点云配准的精度。

1 本文方法

1.1 点云特征线提取1.1.1 点云平面分割

点云平面分割，主要是基于点云局部特征的一致性进行区域增长，将建筑物墙面、屋顶区域分割成多个同质区域。考虑到待分割目标为平面上的点，为了快速得到建筑物点云的平面区域，本文首先利用建筑物点云构建kd-tree［15］，在此基础上通过PCA 变换分析方法估算点云的法向信息［16］，然后从任一种子点开始，以法向一致性进行邻域点的判断，实现平面区域增长。区域增长条件可表示为：

其中：pi为种子点；pj为邻域点；Npi与Npj分别为两点处的法向量；thdvv为顶点距离阈值；thθ为法向夹角阈值。

由于区域增长过程中种子点的选择具有一定的随机性，上述区域增长结果中，通常会存在同一个平面被分割成多块的现象，因此，需要进行区域合并处理。合并过程如下：对于平面Ri中的每个点pi，遍历其邻域中所有点，如果其邻域点所属的平面号和当前点pi不同，则认为该邻域点所属的平面为当前点所在平面的相邻平面，若二者法向夹角小于夹角阈值thθ，则进行合并处理。

1.1.2 特征线提取及优化

虽然建筑物点云不仅包含屋顶区域，还包括墙面、窗户等区域，经过平面分割处理，各部分基本得到有效分割，为了提取不同区域点簇的特征线，本文直接采用Alpha-shape 算法［17］进行区域轮廓线的提取，在此基础上通过拆分处理得到平面区域特征线。Alpha-shape轮廓线提取过程如下：

1）对于平面点簇S，设定半径阈值α。

2）选取S中任意两点pi、pj，若其连线的长度小于2*α，则根据几何关系可计算过pi、pj圆周的圆心。

3）若点簇S中存在与圆心的距离小于α的点，则表明pi、pj非轮廓点；否则标记pi、pj为轮廓点，其连线即为轮廓线段。

4）继续按步骤2）～3）搜索判断其他点，直到所有点均被处理时停止。

为了便于后续特征线匹配，本文对轮廓线提取结果进行分段和拟合处理得到特征线段。分裂时，利用轮廓线上距离首尾端点所连直线的最大偏差点，将轮廓线拆分成多个子线段；然后，采用最小二乘法拟合方法［18］对轮廓点进一步拟合得到特征线段。

考虑到激光扫描的随机性以及点簇噪声的影响，上述特征线提取结果中，通常会存在因点云分布不均匀或小平面导致的冗余特征线，需要进一步进行优化处理。

1）短线剔除处理。若线段长度小于阈值Th_L，或相邻线段之间角度小于阈值Th_θ，则剔除短线。

2）冗余线段合并。如图1 所示，若线段Li与线段Lj满足如下条件，则进行合并处理。

其中：dLi和dLj分别是从原点到Li和Lj所在直线的距离；L是投影区域长度；ε为比例系数；max{dprj}为Lj的两个端点与线段Li的垂直距离最大值；davg为该组点云的平均点间距。

合并处理时，将Lj端点投影在线段Li上，并取4 个端点中距离最远的两个点更新Li的端点：若Li距离较远的端点包含线段Lj投影端点，则将Lj的投影端点作为Li新的端点，图中L*线段为线段合并后得到的新线段。

图1 冗余线段合并示意图Fig.1 Schematic diagram of redundant line segment merging

1.2 点云配准

1.2.1 配准基元和相似性测度

三维空间中，若要解算两组点云的有效变换矩阵，至少需要两对非平行直线。为了保证匹配的可靠性，本文针对上述优化处理的结果，进一步筛选有效的特征线对作为配准基元。若相邻线段满足以下条件，则该配准基元有效。

如图2所示，d为相邻线段最邻近端点的距离，θ表示两条相邻线段的夹角。

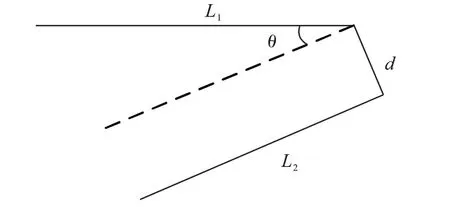
图2 配准基元示意图Fig.2 Schematic diagram of registration primitive

而同名特征的判断，以线对夹角和线段长度作为相似性测度。对于两组点云p和q，L1表示线对中长线段的长度，L2表示线对中短线段的长度，dp和dq分别为两组点云的平均点间距。如果两组点云中的线对满足式（4），则将其视为同名线对。

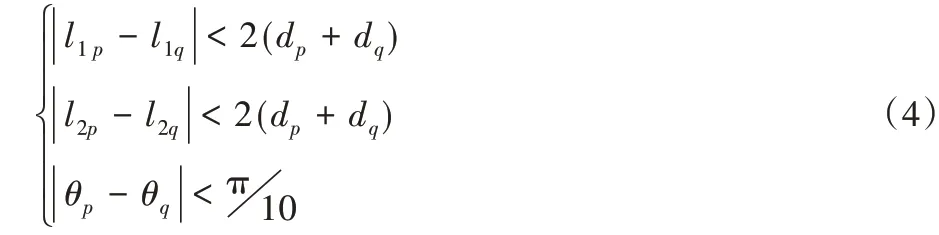
1.2.2 点云粗配准

根据相似性测度，在两个待配准点集中寻找同名线对，并以线对的端点作为同名点，解算最终变换模型。为得到最优变换关系，本文采用如下方法迭代遍历两组点集中的线对，得到最佳的匹配结果：

1）基于两组点集中的配准基元，利用相似性测度在两组点集中查找匹配同名线对，并以线对端点坐标，采用四元数法［19］解算初始变换矩阵。

2）利用初始变换矩阵处理待配准点集中的线特征，将待配准点集转换至目标点集中。

3）统计变换后的待配准点集与目标点集中同名线段的个数。

4）重复步骤1）～3），逐个遍历点集中的配准基元，得到变换后的待配准点集与目标点集中同名线对的个数，取同名线对数目最多时的变换矩阵作为最优匹配结果。

5）为了使刚性变换矩阵解算结果更加准确，利用所有同名线段的端点坐标解算变换矩阵，并以此作为点云粗配准结果。

1.2.3 点云精配准

考虑到基于点云的特征线的提取会存在一定的误差，因此本文在基于特征线匹配的基础上，进一步采用ICP 算法进行两组点集的迭代配准，以提高配准结果的精度，步骤如下：

1）对于粗配准点集P和Q，在点集P中寻找与Q对应的点，生成对应点对。2）通过四元数法计算旋转平移的6个参数及变换矩阵R。3）对点集P使用上述变换矩阵R进行旋转和平移，得到新的点集P'。

根据点集P'和Q中的对应点的平均距离来确定是否继续迭代。因此，求解最佳变换矩阵的问题，可以转化为计算使f(R，T)的值最小时的旋转矩阵R和平移矩阵T；

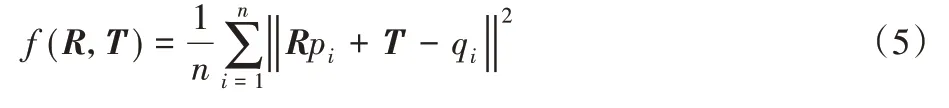
4）若继续迭代，更新待配准点云的位置，继续步骤1）；否则结束迭代，得到最终的配准结果。

2 实验与结果分析

为了验证本文算法的有效性，采用了两组具有不同重叠度的建筑物点云数据进行实验。两组数据均是利用地面激光雷达设备从不同角度采集的建筑物点云，为部分重叠点云，其中点集Ⅱ的重叠区域较小，受遮挡严重，点云渲染结果如图3所示。两组点云的统计信息如表1 所示，由表1 可以看出：点集Ⅰ的最大平均间距为0.053 m，点云密度较为稀疏，而点集Ⅱ的最大平均点间距为0.019 m，点云相对稠密。

图3 实验区域点云渲染效果图Fig.3 Rendering effect diagrams of point clouds in experimental regions

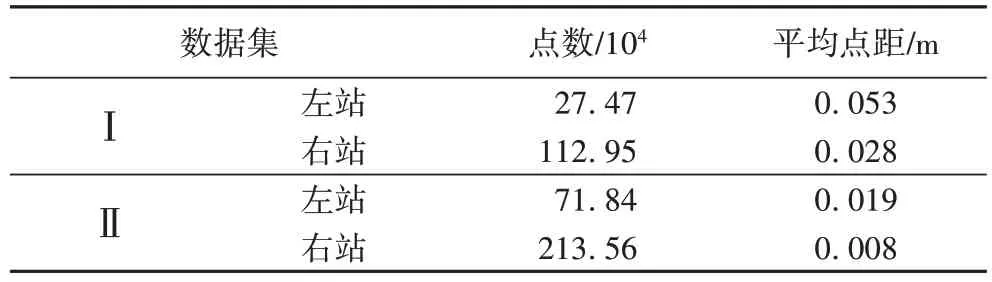
表1 点云信息统计Tab.1 Statistical information of point clouds

图4 是两组点云的平面分割结果，为了便于说明，此处只针对每个数据集的左站点云处理结果进行展示分析。图4中，图（a）、（c）是直接基于点云法向一致性进行区域增长的结果，从图中可以看出，很多共面区域被分成了多个小面片，由于该方法的区域增长范围被限制在该平面初始种子点的周围，因此提取得到的小平面呈现出以初始种子点为圆心的圆形区域，对此需要进行区域合并处理；图（b）、（d）为基于平面法向的平面区域合并结果，可以看出，位于同一平面上的多个小平面已经被正确合并，形成较为完整的墙面，墙面结构更加清晰。

图5 是两组点集的直线段提取结果，其中：图（a）、（c）是直接基于投影点集提取的直线段，图（b）、（d）为优化后的直线段结果（Th_L=0.5，Th_θ=10，ε=0.05）。从图5（a）、（c）中可以看出，两组点云中均提取了丰富的结构信息，提取的结果能基本反映出建筑物表面的细节信息，但由于平面分割等因素，特征线中存在冗余线段；从图5（b）、（d）优化结果可以看出，优化后冗余线段被有效合并，短线被正确剔除，特征线更加简洁，能清晰表达建筑物屋顶及墙面特征。

基于特征线提取结果进行同名线段的匹配，匹配结果如表2 所示。从表2 中可以看出，数据集I 中大部分特征线得到有效匹配，而数据集Ⅱ由于重叠区域较少，虽然左右测站具有丰富的线特征，但寻找到的同名线段数目较少，只有23 对正确匹配的同名线段。

图4 点云平面分割结果Fig.4 Plane segmentation results of cloud points

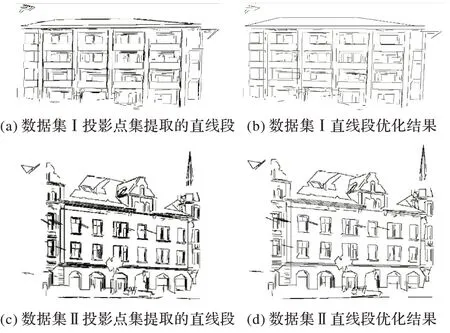
图5 特征线段提取结果Fig.5 Extraction results of feature line segments

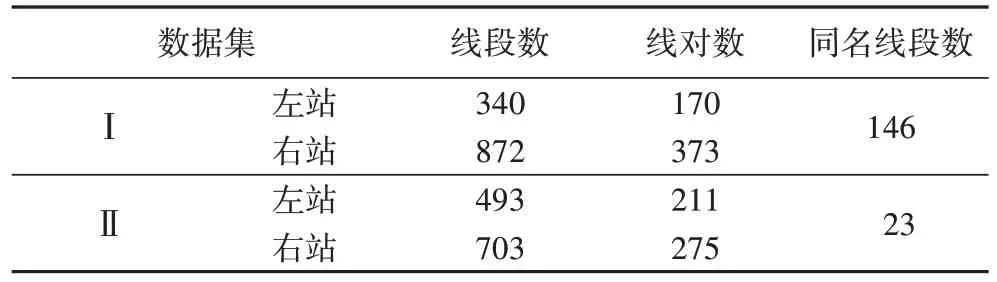
表2 线段提取及匹配结果统计Tab.2 Statistics of extraction and matching results of feature line segments

图6 为建筑物点云配准结果图，图（a）为数据集Ⅰ的配准结果，图（b）为数据集Ⅱ的配准结果。从图6 中可以看出，两组数据集重叠区域均正确地重叠在一起。

图6 点云配准结果Fig.6 Registration results of point clouds

图7 为配准结果局部剖面图，从图7 中可以更清楚地看出，不同测站的墙面点云较好地吻合在一起，表明实验区域点云得到较好的配准。

图7 配准结果局部剖面图Fig.7 Part sectional drawings of registration results

为了进一步验证方法的性能，将本文方法配准结果与经典ICP 算法结果进行对比分析。由于两组数据集均为部分重叠，经典ICP 算法不能收敛到正确位置。本文以手动给定位置初值的ICP配准结果作为参照，分析经典ICP算法以及本文方法的配准结果，并统计配准结果对应点之间的最大距离误差、平均距离误差以及均方根误差（Root Mean Square Error，RMSE）。RMSE计算式如下：

其中：g是点集数量；di是本文方法与手动配准结果的对应点的距离。

点云配准误差统计分析结果如表3 所示。从表3 中可以看出，经典ICP 算法配准结果与手工初值的配准结果具有较大误差，特别对于数据集Ⅱ，RMSE 达到0.245 m，表明对于部分重叠的建筑物点云，经典ICP 算法难以收敛到正确的位置；而本文方法结果与经典ICP 算法结果相比，配准精度有了明显提高，两组数据集的平均误差分别为0.042 m 和0.044 m，表明基于特征的粗配准方法与手工给定初值的配准方法得到的结果精度相当，基于特征的粗配准能为ICP 配准提供有效的初值位置，提高ICP算法的稳定性。

表3 点云配准误差统计分析 单位：mTab.3 Statistics and analysis of registration errors of point clouds unit：m

此外，对比点云信息统计表1以及点云重叠情况（见图4）可以发现，在平均点间距方面，数据集Ⅰ大于数据集Ⅱ，但二者的RMSE 相当，分别为0.051 m 和0.053 m，分别为其点云最大平均点间距的0.96倍和2.79倍，表明点云配准精度不仅与点云密度相关，还受到点集重叠区域大小影响，点云密度越高，重叠度越大，配准结果的可靠性越高。

3 结语

地基建筑物点云配准对于获取完整的建筑物信息、构建建筑物三维模型具有重要意义。本文在分析点云配准现状的基础上，根据优势互补的思想，提出了一种基于线特征及ICP算法的地基建筑物点云配准方法。该方法在建筑物点云平面分割的基础上，通过轮廓线检测以及分裂拟合处理，得到建筑物丰富的特征线；然后，以特征线对作为配准基元，根据线段夹角及距离等相似性测度实现点云的粗匹配，在此基础上利用ICP 算法完成建筑物点云精确配准。通过两组实地数据进行实验验证，实验结果表明，基于线特征的由粗到精的点云配准方法能改善ICP 算法对点云初值的依赖，特别是可以克服ICP 算法针对部分重叠区域点云易陷入局部最优的不足，提高了配准方法的稳定性。下一步研究将集中在地物其他特征的提取及匹配方面，以降低方法对线特征的依赖，提高其通用性。