基于视频排队长度管理的小步增减绿信比优化方法
2020-06-20吴益源连培昆郭建钢赖元文康雅玲
吴益源,连培昆*,郭建钢,赖元文,康雅玲
(1.福建农林大学交通与土木工程学院,福州 350002;2.福州大学土木工程学院,福州 350116)
(∗通信作者电子邮箱peikun_lian@163.com)
0 引言
交通信号配时优化可提高城市路网的交通运行效率,可有效地缓解交通拥堵。相较于离线的信号配时优化,实时在线的信号配时优化可提高交通信号控制系统的自适应能力,可适应复杂的交通流变化。随着我国机动车保有量的快速增加[1],城市路网的交通负荷不断加大,交叉口排队溢出状况不断加剧,传统的自适应控制技术已经无法满足现有的交通管理控制要求,急需对传统的自适应控制技术进行改进。
悉尼自适应交通控制系统(Sydney Coordinated Adaptive Traffic System,SCATS)[2-5]采用小步增减绿信比(Incremental Split Selection,ISS)优化方法,ISS 通过每个周期对设置相位进行小量调整来降低最忙相位的饱和度,使得各个相位的饱和度处于均衡状态,可提供无限量的绿信比方案,提高了系统的自适应能力[6-7]。但该研究方法依赖于检测数据的准确性,一旦检测线圈损坏将产生不合理的绿信比方案,严重影响交叉口的车辆运行效率;且当到达的车辆数多于相位绿灯时间所能通行的最大车辆数时,检测数据难以反映排队长度的空间分布,使得该优化方法在长队列状态下效果欠佳[8]。
随着4G、5G 通信技术及计算机图像视频技术的发展,交通管理部门可通过实时视频查看或实时视频图像识别,获取交叉口各进口道的排队状况,并结合自身经验或模型算法进行信号配时优化[9]。在此背景下,通过实时在线视频,基于排队长度的小步增减绿信比优化方法无需考虑检测线圈的运维问题,且能直观地获取路段的排队长度状况,利于绿信比方案的准确制定。
区别于传统的排队长度指标,先前研究并未将每个相位红灯刚结束时的排队长度和绿灯刚结束时的排队长度进行统一考虑[10-15]:前者与路段排队溢出有关,可作为相位优先控制的依据指标[16];后者与相位绿灯时间有关,可作为判断当前相位绿灯时间是否匹配车辆到达数的依据,可为绿信比小步增减量的确定提供依据[17]。基于以上分析,本文将对上述两个排队长度指标进行组合建模,提出基于视频排队长度管理的小步增减绿信比优化方法,该优化方法将充分考虑多相位排队平衡、排队溢出、相位优先设定、周期长度固定与否、单位优化时间等条件。
1 小步增减绿信比优化模型
如图1 所示,在红灯结束时刻,相较于西进口道,南进口道的排队长度较短,但分配到南进口道的绿灯时间又相对较长,由此将导致该相位绿灯时间的浪费。相较于南进口道,西进口道的排队长度较长,但分配到西进口道的绿灯时间又相对较短,该相位的通行需求将得不到保证,有可能导致排队溢出现象的发生。鉴于此,本文提出了小步增减绿信比优化模型,该模型通过对相位绿灯时间进行实时动态调整,从而实现各相位绿灯时间与各进口道排队长度的动态平衡,以提高交叉口的通行效率。

图1 小步增减绿信比优化模型示意图Fig.1 Schematic diagram of incremental split selection optimization model
对于基于排队长度指标的小步增减绿信比优化模型,各相位绿灯时间增减量的确定主要包含三个阶段。第一阶段:通过实时视频查看或实时视频图像识别获取各相位红灯结束时的排队长度,从而计算各相位绿灯结束时的排队长度,并据此计算当前信号周期各相位的绿灯时间增减量,达到均衡各进口道排队长度的目的;依据周期长度固定与否,对绿灯时间增减量进行第一阶段周期平衡调整。第二阶段:依据防排队溢出设定及相位优先设定,判断红灯结束时的排队长度是否大于最大排队长度阈值,从而调整当前信号周期各相位的绿灯时间增减量;依据周期长度固定与否,对绿灯时间增减量进行第二阶段周期平衡调整。第三阶段:依据最小绿灯时间设定,判断相位绿灯时间是否小于最小绿灯时间阈值,从而调整当前信号周期各相位的绿灯时间增减量;依据周期长度固定与否,对绿灯时间增减量进行第三阶段周期平衡调整。具体计算模型如下:
1)依据绿灯结束时的排队长度,计算各相位的绿灯时间增减量:

式中:Qri,j为第i个交叉口第j个相位红灯结束时的排队长度(m);Qri,j,p为第i个交叉口第j个相位第p个进口道方向红灯结束时的排队长度(m),该指标可通过实时视频查看或实时视频图像识别获得。
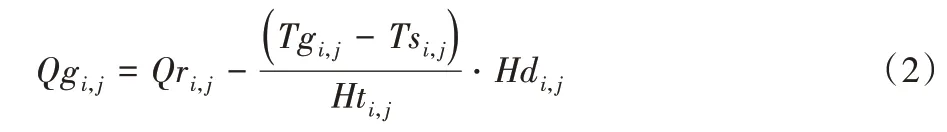
式中:Qgi,j为第i个交叉口第j个相位绿灯结束时的排队长度(m),该排队长度大于零时表示当前相位的绿灯时间无法清空红灯结束时的最大排队长度,反之则表示当前相位的绿灯时间有剩余;Tgi,j为第i个交叉口第j个相位的绿灯时长(s);Tsi,j为第i个交叉口第j个相位的启动损失时间(s),该参数为式(1)中Qri,j,p为最大值时所对应的Tsi,j,p;Hti,j为第i个交叉口第j个相位的饱和车头时距(s),该参数为式(1)中Qri,j,p为最大值时所对应的Hti,j,p;Hdi,j为第i个交叉口第j个相位的饱和车头间距,该参数为式(1)中Qri,j,p为最大值时所对应的Hdi,j,p。

式中:为Qgi,j按从小到大排序后的绿灯结束时排队长度(m);函数Sort_Id()记录排序前后相位编号的映射关系。

式中:Lui为第i个交叉口的单位排队长度(m);Li,j,p为第i个交叉口第j个相位第p个方向的进口道长度(m);αi为第i个交叉口最短进口道长度的分段数量。
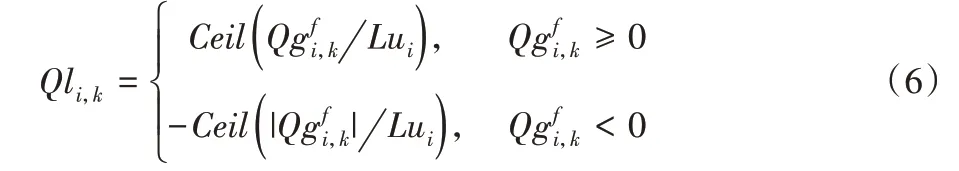
式中:Qli,k为第i个交叉口第Sort_Id(k)个相位的排队长度等级;Ceil为向上取整函数。
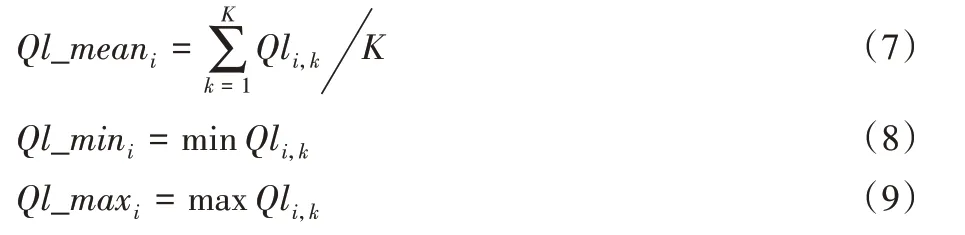
式中:Ql_meani为第i个交叉口的平均排队长度等级;K为第i个交叉口的相位总数;Ql_mini为第i个交叉口的最小排队长度等级;Ql_maxi为第i个交叉口的最大排队长度等级。
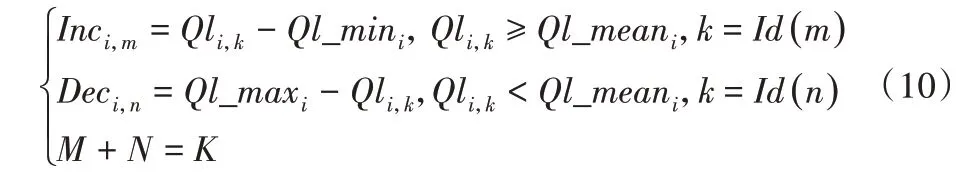
式中:Inci,m为第i个交叉口第Sort_Id(Id(m))个相位的绿灯时间增量(s);函数k=Id(n)为增量相位编号与相位编号的映射关系,函数参见式(3),函数Sort_Id()参见式(4),M为增量相位的个数;Deci,n为第i个交叉口第Sort_Id(Id(n))个相位的相位绿灯时间减量(s),N为减量相位的个数;增量相位与减量相位的个数总和等于第i个交叉口的相位总数K。
式中:为第i个交叉口第Sort_Id(Id(m))个相位第一阶段的绿灯时间增量(s);为第i个交叉口第Sort_Id(Id(n))个相位第一阶段的绿灯时间减量(s)。若无需进行周期平衡调整,该绿灯时间增量或减量将直接代入下一阶段的运算。
2)依据周期长度固定与否,对绿灯时间增减量进行第一阶段周期平衡调整。

式中:Timesi为第i个交叉口绿灯时间总增量与总减量(或总减量与总增量)的倍数;Floor为向下取整函数;Rei为第i个交叉口绿灯时间总增量与总减量(或总减量与总增量)的余数;Mod为求余数函数。

直至Rei(n+1)=0,循环结束。
该周期平衡调整优先把需要平衡的量Rei分配给减量较大的相位或增量较大的相位,从而扩大各相位绿灯时间增减量的差值。
3)判断红灯结束时的排队长度是否大于最大排队长度阈值:

式中:Pre_id(x)为增量相位或减量相位编号与Qgi,j相位编号的映射关系;函数Sort_Id()参见式(4);函数Id()参见式(10)。
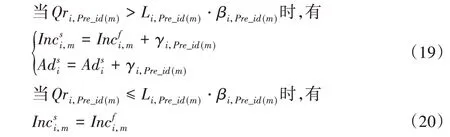
式中:为第i个交叉口第Pre_id(m)个相位第二阶段的绿灯时间增量(s),函数Pre_id()参见式(18);γi,Pre_id(m)为第i个交叉口第Pre_id(m)个相位超过最大排队长度后的绿灯时间增量(s),该参数为式(1)中Qri,Pre_id(m),p为最大值时所对应的γi,Pre_id(m),p;Li,Pre_id(m)为第i个交叉口第Pre_id(m)个相位所对应的进口道长度(m),该参数为式(1)中Qri,Pre_id(m),p为最大值时所对应的Li,Pre_id(m),p;βi,pre_id(m)为第i个交叉口第Pre_id(m)个相位所对应的最大排队长度系数阈值,该参数为式(1)中Qri,Pre_id(m),p为最大值时所对应的βi,pre_id(m),p;Adsi为第i个交叉口第二阶段的绿灯时间调整量(s)。
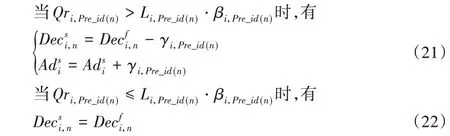
式中:为第i 个交叉口第Pre_id(n)个相位第二阶段的绿灯时间增量(s),其余参数的解释参见式(19)~(20)。
4)依据周期长度固定与否,对绿灯时间增减量进行第二阶段周期平衡调整。

该周期平衡调整把需要平衡的量按减量相位到增量相位的顺序平衡分配给未超过最大排队长队阈值的相位。
5)判断相位绿灯时间是否小于最小绿灯时间阈值。
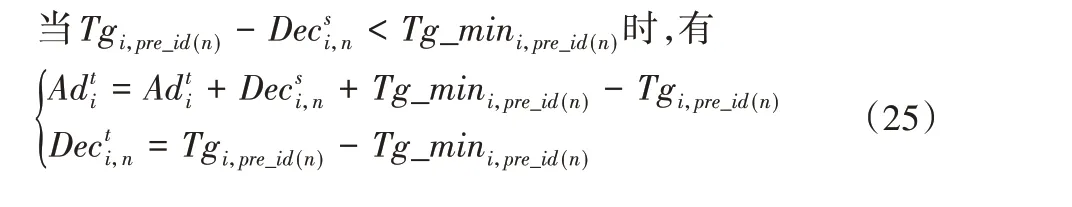
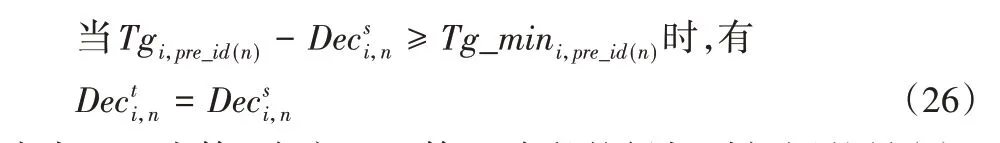
式中:为第i个交叉口第三阶段的绿灯时间调整量(s);Tg_mini,pre_id(n)为第i个交叉口第Pre_id(n)个相位的最小绿灯时间(s),Tgi,pre_id(n)为第i个交叉口第Pre_id(n)个相位的绿灯时间(s),具体参见式(2);为第i个交叉口第Pre_id(n)个相位第三阶段的绿灯时间增量(s)。

式中:为第i个交叉口第Pre_id(m)个相位第三阶段的绿灯时间减量(s)。
6)依据周期长度固定与否,对绿灯时间增减量进行第三阶段周期平衡调整。
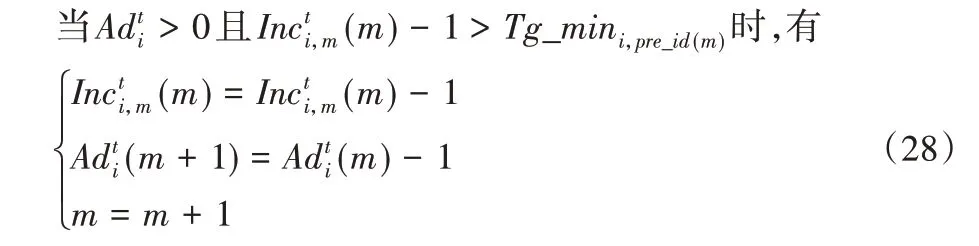
直至(m+1)=0,循环结束。
该周期平衡调整把需要平衡的量分配给数值减去1 s后仍然超过最小绿灯时间阈值的增量相位。

式中:Ami,j为第i个交叉口第j个相位的最终绿灯时间调整量(s);Pre_id-1()为式(18)的反函数;Ωm为式(10)中增量相位的编号集合;Ωn为式(10)中减量相位的编号集合;式(30)中计算得出的Tgi,j为第i个交叉口第j个相位更新后的绿灯时间。
上述公式中,参数αi(式(5))的数值越大,绿灯时间的调整幅度也越大;反之,则相反。βi,j(式(19))的数值越低,则绿灯时间获得增加的可能性越大,则该进口道方向的优先性越高,排队溢出的可能性越低;反之,则相反。当红灯结束时的排队长度超过最大排队长度阈值时,γi,j(式(19))的数值越高,绿灯时间的增量也越大。Tg_mini,j(式(25))的数值设置需考虑行人过街的最小绿灯时间和流量。对于固定周期优化,需要执行式(1)~(30)的运算;对于变周期优化,式(12)~(17)、(23)、(24)及(28)的运算无需执行。
2 模型验证
为了验证模型的优化效果,利用VISSIM(Verkehr In Städten-SIMulationsmodell)仿真软件构建路网交通流环境[18],并利用Visio Studio C# 进行VISSIM 的组件对象模型(Component Object Model,COM)编程[19],以此控制交通仿真的运行和优化配时模型的计算与更新,具体的方法与步骤如下。
步骤1 在VISSIM 仿真软件上构建仿真路网、出入交通量及初始信号配时方案。
步骤2 在数据库输入各交叉口编号i、各交叉口相位编号j、各交叉口各相位各进口道方向的绿灯启动损失时间Tsi,j,p、饱和车头时距Hti,j,p、饱和车头间距Hdi,j,p、路段长度Li,j,p、最大排队长度系数阈值βi,j,p及超过最大排队长度后的绿灯时间增量γi,j,p、各交叉口最短进口道长度的分段数量αi、各交叉口各相位的最小绿灯时间Tg_mini,j、各交叉口各相位各进口道的所有路段编号与对应长度、连接段编号与对应长度、搭接相位的编组数据等信息。
步骤3 编写好自定义信号控制逻辑及仿真运行控制程序。
步骤4 设置好仿真运行控制参数,启动仿真运行。
步骤5 分析仿真导出数据,得出实验结论。
图2 中,ElapsedTime为仿真已运行时间,Cycle_ElapsedTimei为第i个交叉口当前周期已运行时间,Cycle_Timei为第i个交叉口当前周期的周期时长,Red_ElapsedTimei,j为第i个交叉口第j个相位当前红灯状态已运行时间,Red_Timei,j为第i个交叉口第j个相位当前的红灯时长。对于图2,红灯结束时的排队长度由该相位所对应的进口道内所有VISSIM 路段和连接段内所有车辆的速度进行判断所得;对于搭接相位,依据最大排队长度及排队溢出状况,对搭接相位进行分级处理[20],每一级均按小步增减绿信比优化模型进行绿灯时间增减量计算和配时更新。

图2 小步增减绿信比优化方法流程Fig.2 Flowchart of incremental split selection optimization method
3 算例分析
选取福州市的三个交叉口为研究对象,进行算例分析。其中,交叉口1 为五四路—东大路交叉口,交叉口2 为湖东路—井大路交叉口,交叉口3 为乌龙江大道—浦上大道交叉口。所选择的三个交叉口在高峰期间常发生排队溢出现象,引发上下游交叉口的交通拥堵。各交叉口的现状情况见表1~2和图3,其中pcu(passenger car unit)表示标准车当量数。
为了验证小步增减绿信比方法的优化效果,该算例分别进行了参数组合分析、适用条件分析和反应速度分析。

表1 各交叉口交通量单位:pcu·h-1Tab.1 Traffic volume at each intersectionunit:pcu·h-1

表2 各交叉口高峰时段和平峰时段的信号配时方案单位:sTab.2 Signal timing schemes at peak hours and ordinary hours for each intersectionunit:s
图3 各交叉口基本状况Fig.3 Basic situation of each intersection
3.1 实验计划
3.1.1 参数组合实验
按照先分段数量αi,后最大排队长度系数阈值βi,j,p和绿灯时间增量γi,j,p的顺序进行优化。其中:βi,j,p和γi,j,p为对应的组合参数,βi,j,p选取交叉口1 北进口方向、交叉口2 南进口方向以及交叉口3 西进口方向;为满足行人安全过街的需求,最小绿灯时间Tg_mini,j取15 s。评价指标为:排队长度方差。具体实验见表3实验组编号①、②。
3.1.2 适用条件实验
根据3.1.1 节中的实验结果选取最优参数组合,在高峰时段流量的条件下,分别采用现状交叉口高峰时段的配时和平峰时段的配时进行优化仿真。评价指标为:排队长度方差、车均延误和通行能力。具体实验见表3实验组编号③、④。
3.1.3 反应速度实验
为了验证当绿信比与饱和度不匹配时的反应能力,设置交叉口1 南进口左转车道、交叉口2 南进口道和交叉口3 西进口道的流量为零,分析交叉口1 南进口左转相位绿灯时间、交叉口2 南进口相位绿灯时间以及交叉口3 西进口相位绿灯时间的变化情况。评价指标为:绿灯时间变化率。具体实验见表3实验组编号⑤。

表3 实验计划Tab.3 Experimental programs
3.2 结果分析
3.2.1 参数组合分析
如图4~6 所示的实验结果表明,在固定周期和变周期的策略下,αi分别取5~6 和4~6 时是最理想的变化范围;βi,j,p分别取0.6~0.8 和0.6~0.8 时的优化效果更佳;γi,j,p分别取4~6和2~5时的改善效果更好。
其中,对于交叉口1,αi、βi,j,p、γi,j,p分别取5、0.6、6 和6、0.8、2 时是最佳的参数组合;对于交叉口2,αi、βi,j,p、γi,j,p分别取5、0.8、4 和6、0.6、5 时是最佳的参数组合;对于交叉口3,αi、βi,j,p、γi,j,p分别取6、0.7、6 和4、0.7、4 时是最佳的参数组合。不同的交叉口对应不同的信号配时和流量等交通流信息,因此在优化前需重新进行参数组合实验。
3.2.2 适用条件分析
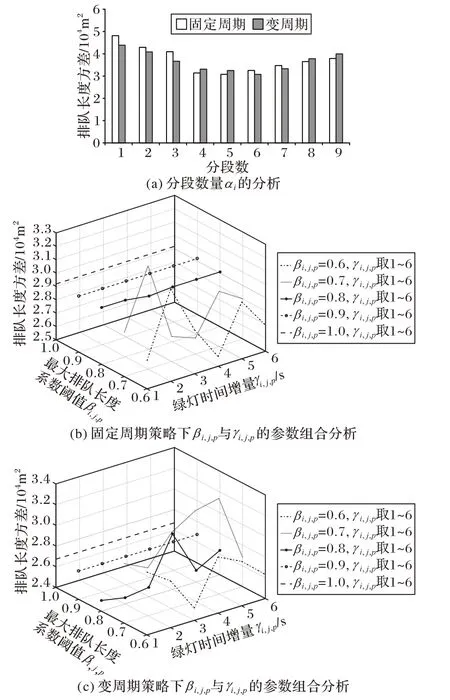
图4 交叉口1参数组合分析Fig.4 Parameter combination analysis of intersection 1
分析各交叉口在高峰时段和平峰时段两种不同配时方案下的优化效果,见表4。表4中,以排队长度方差、车均延误和通行能力为评价指标。
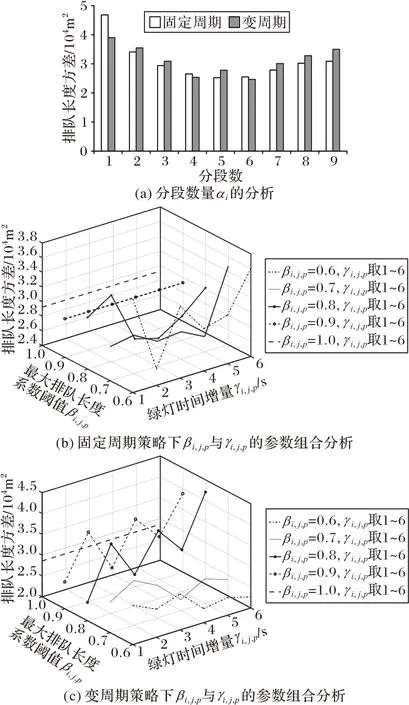
图5 交叉口2参数组合分析Fig.5 Parameter combination analysis of intersection 2
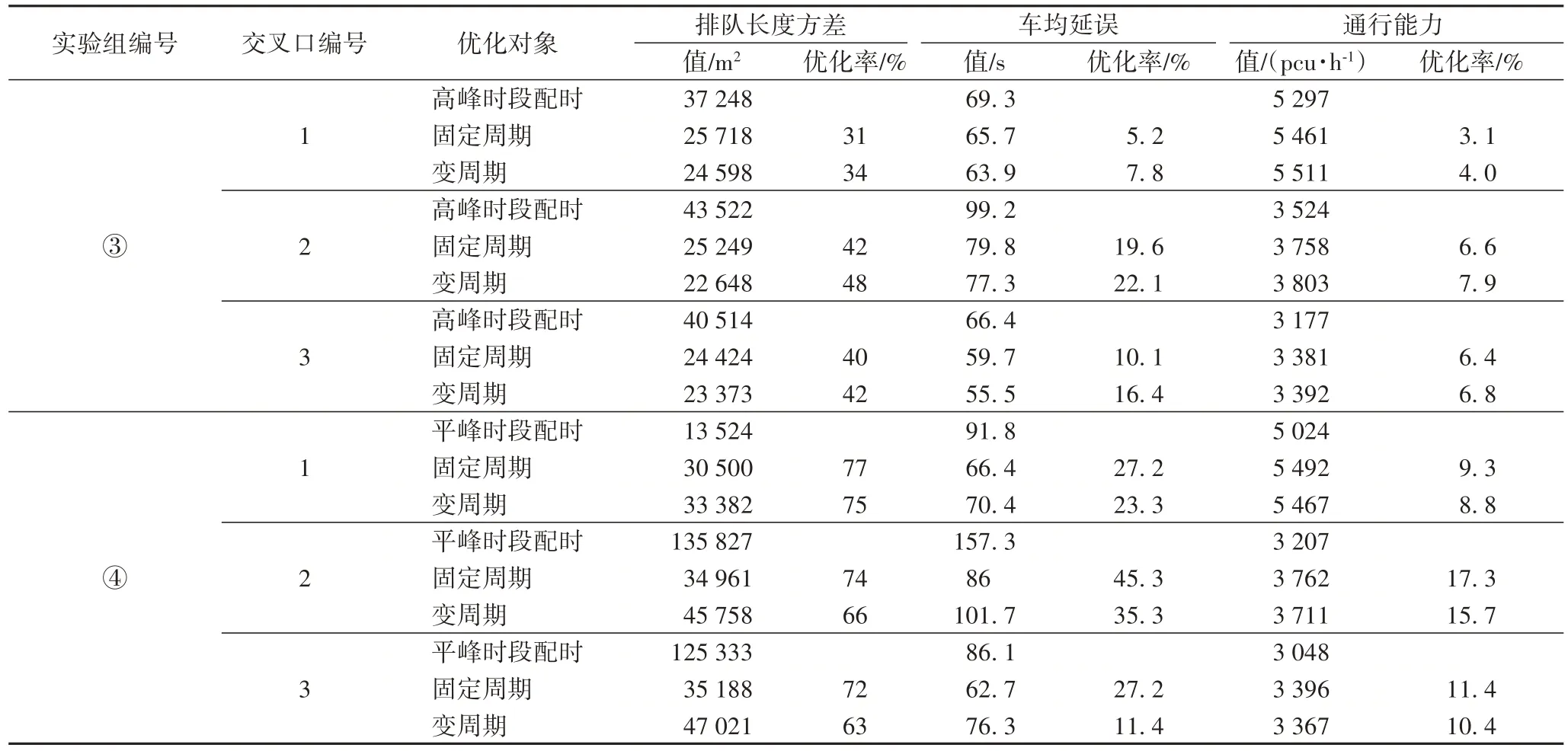
表4 各交叉口优化前后各评价指标对比Tab.4 Comparison of evaluation indexes of each intersection before and after optimization
图6 交叉口3参数组合分析Fig.6 Parameter combination analysis of intersection 3
当绿信比与饱和度相匹配时,变周期策略下的优化效果更佳。对于交叉口1,排队长度方差和车均延误分别下降了34%和7.8%;对于交叉口2,排队长度方差和车均延误分别下降了48%和22.1%;对于交叉口3,排队长度方差和车均延误分别下降了42%和16.4%。当二者不匹配时,固定周期策略下的优化效果更佳。对于交叉口1,排队长度方差和车均延误分别下降了77%和27.2%;对于交叉口2,排队长度方差和车均延误分别下降了74%和45.3%;对于交叉口3,排队长度方差和车均延误分别下降了72%和27.2%。由此可知,本文提出的小步增减绿信比优化方法能够有效均衡各进口道的排队长度,降低车均延误,但对通行能力的提高效果较为有限。
由上述分析可知,当交叉口各进口道出现排队不均衡或溢出的现象时:若交叉口的绿信比与饱和度相匹配,则采用变周期策略下按每周期进行优化的方式效果更好;若二者不匹配,则采用固定周期策略下按每周期进行优化的方式效果更佳。
3.2.3 反应速度分析
由图7 可知,设置交叉口1 南进口左转车道、交叉口2 南进口道和交叉口3 西进口道的流量为零时,在固定周期策略下,交叉口1南进口道左转相位的绿灯时间能在2个周期内迅速从40 s 压缩至26 s,交叉口2 南进口道能在3 个周期内迅速从55 s 压缩至28 s,交叉口3 西进口道能在3 个周期内迅速从58 s 压缩至32 s。此后基于各个进口道排队长度均衡的条件下逐步降至最小绿灯时间Tg_mini,j。这说明当绿信比与饱和度极端不匹配的情况下,小步增减绿信比方法能够在起始阶段快速反应,迅速调节各相位绿灯时间,以此均衡各进口道的排队长度;在变周期策略下,由于变周期不需要进行信号周期的平衡,绿灯时间的增减量调整幅度相对较小,因此变化速度较为缓和。
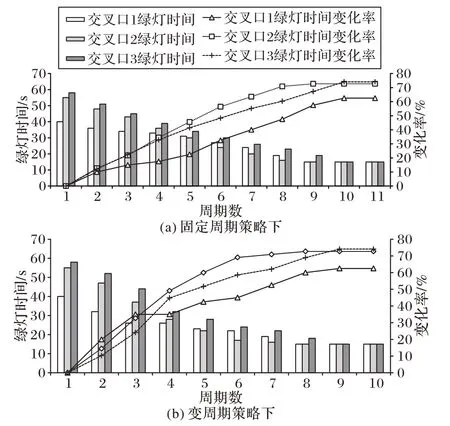
图7 各交叉口绿灯时间变化趋势图Fig.7 Trend of green time at each intersection
4 结语
针对高峰期间交叉口内各进口道排队不均衡或溢出的现象,提出了一种基于视频排队长度管理的小步增减绿信比方法。该方法根据红灯结束时的排队状态及绿灯结束时的排队长度等级,进行各个相位的绿灯时间增减量计算,从而实现各相位绿灯时间与各进口道排队长度的动态平衡。通过参数组合分析、适用条件分析与反应速度分析表明:
1)不同的交叉口对应不同的交通量、信号配时等交通流信息,因此在运用小步增减绿信比方法对交叉口优化前,应重新设定最佳的参数组合。
2)若交叉口的绿信比与饱和度相匹配时,则采用变周期策略下按每周期进行优化的方式效果更好;若二者不匹配,则采用固定周期策略下按每周期进行优化的方式效果更佳。
3)若某一相位的绿灯时间内通过的流量为零时,小步增减绿信比方法可以在短周期内快速调节绿信比,以适应实时的交通流变化。
下一步的研究工作可以尝试在不同的相位组合方面进行改进,并将其运用至线控或面控上。
