基于风速融合和NARX神经网络的短期风电功率预测

徐遵义 王俊雪

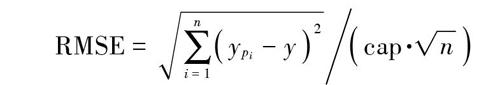
摘  要： 高精度的短期风电功率预测是保证电网日常调度及运行安全的关键因素。目前，国内短期风电功率预测精度普遍低于国外水平。为了提高风机短期功率预测精度，提出一种基于风速融合和NARX神经网络的预测模型。该方法对同一地点不同数据源提供的预报风速进行融合，采用NARX神经网络进行短期风电功率预测。仿真实验结果表明，所提出的短期风电功率预测方法是可行的，预测精度可提高至87.8%，与其他风电功率预测模型相比，具有更高的预测精度和更好的适应性。

关键词：  短期风电功率预测; 预测模型; NARX神经网络; 风速融合; 数据融合; 数据处理

中图分类号： TN99?34; TP391                      文献标识码： A                    文章编号： 1004?373X（2020）09?0166?04

Short?term wind power prediction based on wind speed fusion

and NARX neural network

XU Zunyi， WANG Junxue

（Shandong Architecture University， Jinan 250101， China）

Abstract： High accuracy short?term wind power prediction is the key factor to ensure the daily dispatch and operation safety of power grid. At present， the accuracy of short?term wind power prediction in China is generally lower than that in foreign countries. In order to improve the short?term power prediction accuracy of fan， a prediction model based on wind speed fusion and NARX neural network is proposed in this paper. In the method， fusion of the forecasted wind speed is provided for different data sources at the same location， and NARX neural network is used for short?term wind power prediction. The simulation experiment results show that the short?term wind power prediction method proposed in this paper is feasible， and its prediction accuracy can be increased to 87.8%. In comparison with other wind power forecasting models， it has higher prediction accuracy and better adaptability.

Keywords： short?term wind power prediction; prediction model; NARX neural network; wind speed fusion; data fusion; data processing

0  引  言

随着环境污染、能源紧缺以及电能需求量大等问题的日益突出，风能作为一种具有清洁、储量丰富以及可再生等特点的新能源具有重要的发展前景[1]。由于风的不可控性、间歇性以及随机性等特点，以及国内短期风电功率预测精度普遍较低的现状[2]，研究更高精确度的短期风电功率预测算法对保证风电场的日常调度、电网的平稳运行和提高国内风电利用率具有重要现实意义。短期风电功率预测方法主要有统计方法和物理方法，其中，统计方法中以建立数理统计模型的方法更为普遍。主要的统计方法有：时间序列、支持向量机、灰色关联分析、小波分析和人工神经网络等模型[3?7]，预测精度一般在82%～84%，国外研究机构预测精度已达到85%以上[8]。

风电功率预测的主要依据为气象预报风速，同时，风速与风电功率存在高度非线性关系[9]。因此，本文提出一种基于气象融合的动态神经网络模型对风电功率进行预测，该方法采用基于可信度的加权方法对不同来源的天气预报数据进行融合，采用带外部输入变量的非线性自回归（Nonlinear Auto Regressive with Exogenous inputs，NARX）神经网络对风电功率进行预测。

1  数据融合算法

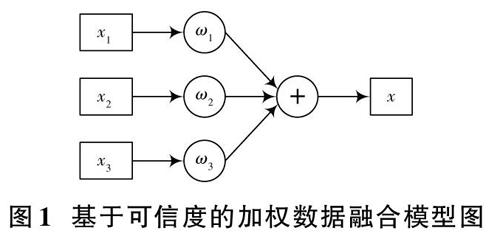
数据融合算法是对多个信息源所提供的关于同一个地点特征信息的多个不准确信息综合后形成的一组相对准确的数据[10]。常用的数据融合模型主要有平均算法数据融合、基于可信度数据融合、D?S数据融合和Kalman滤波数据融合等。由于基于可信度的数据融合算法充分容纳分析了历史预报数据，能够以各个预报数据源的历史气象预报准确性为依据。所以本文中数据融合算法采用基于可信度的数据融合[11?12]。其中，基于可信度的数据融合模型如图1所示。

图1中，[x1，x2，x3]代表不同数据源的测量值;[ω1，ω2，ω3]分别为每个数据源的权值。通过加权数据融合之后的数据值记为[x]：

[x=i=13xiωi] （1）

式中[ωi]为第[i]个数据源的可信度权重因子，且满足[i=13ωi=1]。

本文中可信度权重因子根据各数据源测量值与真实值的相似程度来确定[13]。相关系数[r]为：

[ri=Exi-μxix-μxDxiDx]  （2）

式中：[xi]为第[i]个数据源数值;[μxi]为第[i]个数据源数值均值;[Dxi]为第[i]个数据源测量值方差。

令[ti=r2i]，则第[i]个信息源的可信度权重可表示为：

[ωi=ti?i=13ti-1] （3）

2  NARX神经网络模型

NARX神经网络是一种具有外部输入的非线性自回归动态神经网络，网络的输出不仅仅取决于当前的输入，而且还与过去时刻的输出有关，能够容纳充足的历史数据和数据之间的变化特性，因此，NARX网络模型能够更好地逼近非线性动力学模型[14?15]。

NARX神经网络算法实质是一种时间序列的自回归算法。由于时间序列是线性算法，只能适用于整个序列是平稳序列的条件下[16]。对于非平稳的序列，针对某一段平稳序列可以采用时间序列的自回归算法，对于波动大的时间段时采用logistics函数将其无限接近平稳序列。最终此模型是多个离散的自回归算法加上调节函数的组合，该模型的核心函数如下：

[yt=?0+β1Gx1γT1+εt]    （4）

式中：[?0]为待估计截距项;[β1]为待估计系数;[Gz=11+e-z]，为logistics方程;[x1=1，yt-1，yt-2，…，yt-p];[γT1=γ0，1，γ1，1，γ2，1，…，γp，1T]，为回归模型参数。

整个模型曲线函数为：

[yt=?0+j=1nβjGxtγTj+εt]  （5）

NARX神经网络模型结构图如图2所示。

图2中：[m]为NARX神经网络模型输入时延阶数;[n]为反馈输入时延阶数;[w]为权值向量;[b]为偏置;[d]为隐含层神经元个数;神经网络隐含层激活函数[f1]为双曲正切[S]型传递函数，即tansig函数，其表达式为[fx=21+exp-2x-1] ;神经网络的输出层激活函数为纯线性传递函数，即purelin函数，其表达式为[fx=x]。

NARX神经网络的模型可以定义为：

[yt=fxt-1，xt-2，…，xt-nx，yt-1，yt-2，…，yt-ny] （6）

式中：[f（）]为非线性函数;[yt]为网络模型输出变量;[xt]为网络模型外部输入变量;[xt-1，][xt-2，…，xt-nx，yt-1，yt-2，…yt-ny]为网络模型时延后的输入变量和反馈时延变量。

3  仿真实验

在风电场风电功率预测中，根据风电机组的发电手册，任意时刻的输出功率与对应时刻风速的计算关系如下：

[PVt=0，    vt≤v切入Cvt，    v切入≤vt≤vnormPnorm，    vnorm≤vt≤v切出0，    vt≥v切出] （7）

式中：[vt]表示[t]时刻的风速;[Pvt]表示在[t]時刻的功率;[v切入]表示产生风电功率的最小风速;[Cvt]为[t]时刻风速和功率的函数关系;[vnorm]表示额定风速即满足函数的最大风速;[Pnorm]表示额定功率，即当风速超过额定风速时的功率是定值;[v切出]表示可以发电的最大风速。

3.1  数据集及数据处理

实验数据采用中国华能集团山东某风电场（38.136 127 78 N，117.841 930 56 E）2017年6月实测数据。数据包括风电场风机实测风速及功率数据，风电场服务商从西班牙、美国和欧洲专业气象服务购买的该风电场气象预报数据（国内暂无专业气象服务商提供该项服务）。西班牙气象服务公司每6 h发布一次气象预报数据，美国和欧洲气象服务公司每8 h发布一次气象预报数据，采用克里金法插值获得时间分辨率为15 min的气象预报数据[17]。实验数据选取数据中风机实测风速、实测发电功率以及西班牙、美国、欧洲的预报数据作为原始样本数据，根据式（7）对数据异常值和缺失值进行处理。经过数据预处理后选取6月1日—15日的1 440条数据作为训练集，6月16日—30日数据作为测试数据，预测未来24 h风机功率。训练数据集中各气象服务公司提供的风速预报值与风电场实测风速如图3所示，其中，西班牙气象服务公司提供的风速预报精度较高。

3.2  数据融合

为定量分析各气象服务公司预报风速与实测风速之间的关系，本文选取1天、3天、4天、5天以及7天预报风速与实测风速值，计算其相关系数如表1所示。由表1可知：西班牙气象服务公司提供的预报风速与风机实测风速相关系数最大，4天及更长时间的相关系数急剧减少，相关性降低，因此，本文选用最近3天数据计算其相关系数。

基于可信度加权融合算法对不同数据源预报风速进行融合，融合前后的对比如图4，图5所示，融合后的预报风速与实测风速相关系数为0.901 5。

3.3  NARX神经网络模型预测

3.3.1  预测模型评价标准

NARX预测模型采用平均绝对误差MAE、均方根误差RMSE和相关系数[r]进行评价[18]。平均绝对误差和均方根误差用来衡量预测功率与实际功率之间的差值，其值越小，则表示模型的预测精度越高;相关系数用来衡量预测功率与实际功率的拟合程度，相关系数越大，则拟合程度越好。

平均绝对误差[MAE]公式如下：

[MAE=i=1nypi-ycap?n] （8）

均方根误差[RMSE]公式如下：

[RMSE=i=1nypi-y2cap·n] （9）

相关系数[r]的计算公式如下：

[r=i=1nypi-y·y-yi=1ny-y2·i=1nypi-y2] （10）

式中：[yp]为预测功率;[y]为实际功率;[cap]为当前风电场开机容量;[n]为预测时间点个数。

3.3.2  仿真实验结果

采用数据融合后的预报风速作为NARX神经网络的输入向量，风电场发电功率作为NARX神经网络的输出向量。采用单一预报风速与融合风速风电功率预测比较图如图6所示。

为了对本文提出算法与已有算法对风电功率预测精度进行对比，本文对BP神经网络预测模型、NARX神经网络预测模型、基于数据融合的BP神经网络预测模型与基于数据融合的NARX神经网络预测模型进行仿真，结果如表2和图7所示。各个预测模型的预测值曲线和风机的实测功率值曲线的拟合度验证了基于气象融合和NARX神经网络预测模型结果相比于其他三种预测模型，精度可以达到87.9%，预测结果与真实值具有更高的拟合度，更加接近真实值。

4  结  论

针对短期风电功率预测，本文提出一种基于风速融合和NARX神经网络的预测模型。此预测模型可利用多个预报数据源的不同精度，基于可信度为各个预报数据源分配不同的权重进行数据融合;将融合后的风速值作为NARX神经网络预测模型的输入，构建NARX神经网络模型预测风电功率。仿真实验结果表明：NARX神经网络以其良好的非线性映射能力，用于短期风电功率预测是行之有效的，通过与多种现有预测模型进行对比，基于数据融合和NARX神经网络模型预测风电功率具有更高的精度和更好的适应能力。

参考文献

[1] 钱政，裴岩，曹利宵，等.风电功率预测方法综述[J].高电压技术，2016，42（4）：1047?1060.

[2] 薛禹胜.关于短期及超短期风电功率预测的评述[J].电力系统自动化，2015，39（6）：141?151.

[3] 李军，李大超.基于优化核极限学习机的风电功率时间序列预测[J].物理学报，2016，65（13）：33?42.

[4] ZENG Jianwu， QIAO Wei. Short?term wind power prediction using a wavelet support vector machine [C]// 2013 IEEE Power & Energy Society General Meeting. Vancouver， Canada： IEEE， 2013： 1.

[5] 李俊芳，张步涵，谢光龙，等.基于灰色模型的风速：风电功率预测研究[J].电力系统保护与控制，2010，38（19）：151?159.

[6] CATAL?O J P S， POUSINHO H M I， MENDES V M F. Hybrid wavelet?PSO?ANFIS approach for short?term wind power forecasting in Portugal [J]. IEEE transactions on sustainable energy， 2011， 2（1）： 50?59.

[7] LIN Yujie， KRUGER U， ZHANG Junping， et al. Seasonal analysis and prediction of wind energy using random forests and ARX model structures [J]. IEEE transactions on control systems technology， 2015， 23（5）： 1994?2002.

[8] 中国电力科学院.国外风电功率预测发展现状[EB/OL]. [2014?1?1]. http：//www.doc88.com/p?5939751153777.html.

[9] 王勃，冯双磊，刘纯.考虑预报风速与功率曲线因素的风电功率预测不确定性估计[J].电网技术，2014，38（2）：463?468.

[10] YU Zheng. Methodologies for cross?domain data fusion： an overview [J]. IEEE transactions on big data， 2015， 1（1）： 16?34.

[11] ANAND A， RAMADURAI G， VANAJAKSHI L. Data fusion?based traffic density estimation and prediction [J]. Journal of intelligent transportation systems， 2014， 18（4）： 367?378.

[12] 杨红果，申德荣，寇月，等.基于可信度的投票列表合并算法[J].东北大学学报（自然科学版），2016，37（2）：165?168.

[13] 闫鹏飞，孙权.基于可信度加权融合方法在维修性评价的应用[J].计算机仿真，2010，27（6）：31?35.

[14] JAWAD M， ALI S M， BILAL Khan， et al. Genetic algorithm?based non?linear auto?regressive with exogenous inputs neural network short?term and medium?term uncertainty modelling and prediction for electrical load and wind speed [J]. Journal of engineering， 2018， 2018（8）： 721?729.

[15] 付青，单英浩，朱昌亚.基于NARX神经网络的光伏发电功率预测研究[J].电气传动，2016，46（4）：42?45.

[16] JANACEK G. Non?linear time series models in empirical finance [J]. Journal of the royal statistical society， 2010， 52（4）： 696?696.

[17] 中华人民共和国国家能源局.DL/T1711?2017中华人民共和国电力行业标准[S].北京：中国标准出版社，2017.

[18] 徐曼，乔颖，鲁宗相.短期风电功率预测误差综合评价方法[J].电力系统自动化，2011，35（12）：20?26.