基于小波降噪的雷达时频信号互相关测速算法
2020-06-19李佳曹林王东峰付冲
李佳 曹林 王东峰 付冲


摘 要: 为提高基于FMCW体制的双波束车流量雷达的测速精度,对其信号特征进行分析,结合Burg和广义互相关理论,提出基于小波降噪的时频信号互相关测速算法(CC?BWT)。首先,利用最大熵功率谱估计的Burg方法得到雷达回波的频谱信息,通过CFAR检测出目标车辆后提取车辆的时频信号;然后,对时频信号进行小波分解,以改进的阈值函数作为降噪依据进行信号重构,之后两路信号做互相关,估计出时延,从而测得车辆速度。结合仿真和实测数据,并与相位法和双谱法进行对比,验证了该算法的测速准确度达到96%以上且算法鲁棒性好。
关键词: 互相关测速; 时频信号提取; 小波降噪; 最大熵谱估计; 信号重构; 车辆测速
中图分类号: TN957.51?34 文献标识码: A 文章编号: 1004?373X(2020)09?0014?07
Wavelet denoising based cross?correlation velocity detection algorithm
of radar time?frequency signal
LI Jia1, CAO Lin1, WANG Dongfeng2, FU Chong3
(1. Department of Communication Engineering, Beijing Information Science & Technology University, Beijing 100101, China;
2. Beijing TransMicrowave Science and Technology Co., Ltd., Beijing 100018, China;
3. School of Computer Science and Engineering, Northeastern University, Shenyang 110004, China)
Abstract: The signal features of FMCW (frequency modulated continuous wave) are analyzed to improve the accuracy of FMCW system based speed detection of dual?beam vehicle flowrate radar. In combination with the Burg and generalized cross?correlation theory, a time?frequency signal cross?correlation algorithm based on Burg and wavelet transform (CC?BWT) is proposed. Firstly, the frequency spectrum information of radar echo is obtained with the Burg method based on the maximum entropy power spectrum estimation and the time?frequency signal of the vehicle is extracted after the target vehicle is detected with CFAR. And then, the time?frequency signal is subjected to wavelet decomposition to reconstruct the signal by taking the improved threshold function as the denoising basis, then the two signals are correlated for the estimation of the delay and the vehicle speed is obtained finally. It is compared with the phase method and the bispectrum method in combination with the simulation and measured data. The comparison results verify that the speed detection accuracy of the algorithm is above 96% and its robustness is good.
Keywords: cross?correlation velocity detection; time?frequency signal extraction; wavelet denoising; MESE; signal reconstruction; vehicle velocity detection
0 引 言
双波束雷达[1]测速原理如图1所示,利用车辆经过两个波束的时间差[τ]和两个波束的间距[d]计算车辆的速度[v],公式可以简化理解为:
[v=dτ] (1)
目前,应用到车流量雷达测速的方法有以下几种:利用雷达处理机内部定时器记录车辆驶离雷达照射区域时间,利用距离变化率测速,相位法、双谱法和广义互相关法[2]等。这些方法的共同点是通过车辆经过两个雷达照射区域的时间差来间接计算车速。近年来提出了很多关于时延估计的改进算法,如基于马尔科夫链蒙特卡洛的时延估计方法[3]、基于最小均方误差的自适应时延估计方法[2]、基于匹配追踪的稀疏重构时延估计算法[4]、奇异值分解的HB加权广义互相关时延估计[5]、基于中国余数定理的跳频信号时延估计方法[6]、基于双通道DFRFT互谱法的Chirp信号时延估计[7]、基于频率加权的时延估计算法[8]等。这些方法有效地改进了时延估计的精度,但是不能用于信噪比低或非平稳信号的环境,有时甚至需要知道信号和噪声的先验知识,这些往往不易获得。在实际应用的场景中,路面的杂波干扰以及运动目标强度的不断变化,使得实际接收到的雷达信号是非平稳的,且和噪声相关。
本文提出一种基于Burg和小波变换的时频信号互相关算法(Cross Correlation Algorithm Based on Burg and Wavelet Transform,CC?BWT),利用Burg算法及CFAR检测出目标车辆,提取出目标车辆时频信号后进行小波降噪,对降噪后的I,Q两路目标车辆的时频信号做互相关,求出时延并测速。该方法提高了信噪比,增加了信号互相关的估计精度,能有效提高测速准确率。
1 CC?BWT算法
本文测速算法流程图如图2所示,分为车辆时频信号提取和时延估计两部分。
2 获取目标车辆时频信号特征
获取目标车辆的时频信号特征是进行车速测量的必要准备。本文的实验载体是北京川速微波科技有限公司的双波束车流量交通雷达,主要应用于城市交通道路,用于车流量统计和车速检测。
2.1 雷达初始数据
双波束车流量雷达采用调频连续波(Frequency Modulated Continuous Wave,FMCW)体制[9?10],发射波为频率随时间变化的锯齿波,其测距公式如下:
[R=cTΔf2B] (2)
式中:[R]为雷达到目标的距离;[c]为光速;[T]为发射信号周期;[Δf]为发射信号和接收信号的差频;[B]为信号带宽。
雷达侧向安装于道路一侧,其照射区域可以覆盖多个车道,如图3所示。
双波束雷达采集的回波数据每[N]个数据为一帧,一共[M]帧,经处理后的数据样本集合为[x(n)={x(1),x(2),…,x(M);x(i)∈RN}]。其中,[x(i)]代表第[i]帧的[N]个数据。
2.2 基于AR模型的Burg算法
AR模型参数求解以线性预测理论[11]为基础,发展了很多的算法,主要有Yule?Walker法、协方差法、Burg法和改进的协方差法,Burg算法以其良好的分辨率和稳定性获得广泛应用。
Burg算法主要是先根据前向和后向预测误差功率的平均值最小准则估计出反射系数,定义前向和后向误差分别为[ef(n)]和[eb(n)],令前向和后向预测误差平均功率之和为最小,得到:
[efm(n)=efm-1(n)+kmebm(n)ebm(n)=ebm-1(n-1)+k*mefm-1(n)ef0(n)=x(n)] (3)
式中:[km]为反射系数,[k*m]为[km]的共轭;[efm(n)]为[m]阶前向预测误差;[ebm(n)]为[m]阶后向预测误差。
可求出反射系数如下:
[km=-2n=mN-1efm-1(n)eb*m-1(n-1)n=mN-1efm-1(n)2+n=mN-1ebm-1(n-1)2] (4)
式中:[m=1,2,…,p],[p]为模型的阶数。
用Levinson递推算法,由反射系数求出AR模型参数,计算功率谱密度为:
[P(ω)=σ211+k=1pake-iωk2] (5)
式中:[p]为模型的阶数;[ak]为AR模型参数。
2.3 CFAR检测及目标车辆判断
恒虚警检测(Constant False Alarm Rate,CFAR)算法根据信号的特征得到一个自适应动态门限,使雷达的虚警率保持不变,从而使雷达具有良好的检测性能[12]。
将雷达每帧信号的频谱能量信息作为恒虚警检测方法的输入信号[f],通过[fi]左右各[L]单元[{fi-L,…,][fi-1,fi,fi+1,…,fi+L}] ,计算此时杂波背景的均值估计[μ]:
[μ=1(2L+1)n=-LLxi+n] (6)
式中[μ]为通过恒虚警得到的基本阈值。
因此,可以把检测门限定义为:
[U0=Cμ] (7)
式中[C]为检测门限的乘性因子,用于调节虚警率。
当连续多帧被检测为目标时,认为此时有目标车辆经过雷达照射区域,将一辆车行驶过程的时频信息记为如下表达式:
[X(j)=(f(j)1,f(j)2,…,f(j)M)] (8)
式中:[f(j)i]表示第[i]帧信号在[j]频点的频谱幅度值;[X(j)]表示每帧信号在[j]频点的频谱幅度集合。此处频点[j]代表目标车辆距离雷达的距离信息,不同频点代表车辆所在的车道不同;帧号代表时间信息。因此,[X(j)]表示在第[j]频点所对应的车道上,车辆经过雷达照射区域时的时间?频率信号特征。
2.4 提取时频信号的算法流程
获取目标车辆时频信号特征的流程图如图4所示。
获取目标车辆时频信号特征的主要步骤如下:
1) 雷达数据初始化预处理,通道分离成[I,Q]两路,之后去除噪声、直流、畸变点,并加窗。
2) 对预处理后的数据利用Burg算法处理,得到回波信号的频谱能量信息[f]。
3) 对频谱信号进行CFAR目标检测,及多帧目标匹配,以确定目标车辆[k]。
4) 对于确定为目标的车辆,提取车辆的时频信号特征[X(j)I],[X(j)Q]。
利用Burg方法处理雷达回波数据后得到的频谱三维图如图5所示。图中两个能量较高的包络是行驶的车辆信号,坐标点:(12,1 600+:1 800-),(27,1 200+:1 500-)表示在12频点对应的车道,车辆在1 600帧处驶入雷达照射区域,在1 800帧处驶离雷达照射区域。在27频点对应的车道,车辆在1 200帧处驶入雷达照射区域,在1 500帧处驶离雷达照射区域。
分析时频信号[X(27)I],[X(27)Q],如图6所示。[I],[Q]兩路信号之间时频特性基本一致,只是在时间上略有延迟。
3 时延估计
本节主要介绍CC?BWT算法的第二步,即对提取的车辆时频信号进行时延估计。 首先分析传统广义互相关算法的不足,然后通过小波降噪并改进阈值函数的方式改进原有算法,并给出实现流程。
3.1 广义互相关算法的不足
广义互相关算法是一种简单、高效的时延估计方法,被广泛应用于各种工业场景中。
广义互相关时延估计算法是以空间上互相独立的两个接收信号[x1(t)],[x2(t)]为基础,利用互相关系数大小来衡量两个时间序列在不同时刻的相似程度。假设接收信号如下:
[x1(t)=s(t)+n1] (9)
[x2(t)=s(t-D)+n2] (10)
两个接收信号的互相关函数为:
[Rx1x2=E{x1(t)x2(t+τ)}=Rss(τ-D)] (11)
式中:[s(t)]为源信号;[n]为噪声;[D]为延迟时间。
在[τ=D]处可以检测出一个峰值,利用此峰值可以计算出延迟时间。
在本文的应用场景中,直接采用广义互相关算法来进行时延估计是不合适的。该方法采用的是两个传感器采集的时域信号直接进行互相关处理,只有当信号是平稳的且信号和噪声是相互独立的情况下才能较精确地估计出延迟时间。
在雷达实际应用场景中,地面干扰、周围建筑物干扰、邻车道干扰等,使得接收到的雷达回波信号非平稳且和噪声相关。因此,本文利用小波降噪和广义互相关的理论,以目标车辆时频信号为基础进行时延估计。
3.2 基于小波降噪的时频信号互相关算法流程
通过上节的分析可知,目标车辆的时频信息代表在某车道上一段时间内目标车辆的频谱能量集合。在这个频谱能量集合中包含有目标车辆的频谱能量、噪声带来的频谱能量及频谱泄露的影响。为降低噪声频谱能量及频谱泄露的影响,提出基于小波降噪的时频信号互相关算法,进行一层小波分解的步骤如下:
1) 利用上一节中提到的获取目标车辆时频信号特征的方法提取[XI],[XQ]。
2) 利用选定的小波函数对夹杂有目标车辆和噪声的时频信号进行[N]([N=1,2,…])层分解,分解成低频部分[cai]和高频部分[cdi](通过对实际信号的分析,车辆目标的时频特征对应低频部分,噪声的时频特征对应高频部分),之后逐层对低频(目标车辆信息)进行分解。分解层数的确定依据重构信号是否接近于车辆信号的时频信息。
3) 时频信号的离散小波变换定义为:
[ψm,n(t)=a-12ψm,n(a-m0t-nb0)] (12)
[wI=DWT(am0,nb0am0)=(XI,ψm,n(t))] (13)
[wQ=DWT(am0,nb0am0)=(XQ,ψm,n(t))] (14)
式中:[a]为尺度因子;[b]为平移因子;[ψm,n(t)]为离散小波基。
4) 对高频部分进行阈值处理,得到降噪后的高频系数[cd′i]。
根据雷达时频信号小波变换后的特点,对其阈值函数做了改进,阈值函数的降噪程度依赖于信号的分解层数,阈值函数[CDi,]定义如下:
[λ=σ2log N] (15)
[CDi=sgn(cdi)cdi-λ/i, cdi≥λi0, cdi≥λi] (16)
式中:[N]为信号长度;[σ]为信号噪声强度;[i]为当前信号的分解层数。
信号在不同分解层数下的阈值函数对比如图7所示,分解层数越高,降噪越不明显。
5) 将低频车辆时频信号部分和阈值处理后的高频噪声部分进行逐层重构,直到恢复降噪后的信号[w′I] 和[w′Q]。
6) 对小波降噪后的时频信号求互相关性,记为:
[R(k)=1Mm=0M-1w′I(m)w′Q(m+k)] (17)
相关结果如图8所示,[R(k)]最大峰值处所对应的横坐标记为[kmax]。
7) 计算车速,如下所示:
[v=dt=dτ×ε=d(kmax-M)×ε] (18)
式中:[M]为总帧数;[ε]为两帧之间的中断时间;[d]为两天线之间的距离。
I,Q两路车辆时频信息进行小波降噪过程如图9所示。
4 路测数据验证结果
将本文算法写入车流量雷达DSP模块中,以进行实际路测。观察车流量雷达系统工作的性能情况,连接相机,统计分析车辆有效识别率和车速测量准确率。同时,采集数据进行Matlab仿真,与实测情况相互对比,验证算法的可行性。
测试场景为城市道路,一共六车道,中间存在一个隔离带,将车流量雷达系统安装到道路一侧。
4.1 车辆目标信号提取效果验证
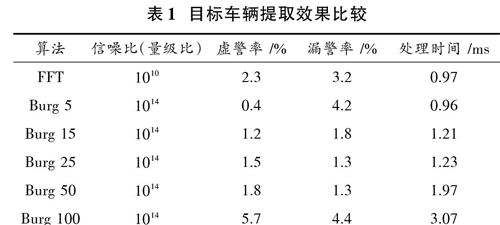
对实测数据进行车辆目标信号提取,在获取车辆信号频谱时分别采用FFT方法和Burg方法,Burg方法又分别采用了不同的阶数,分别为[p=5],[p=15],[p=25],[p=50],[p=100],对比结果如表1所示。由表1可知:Burg算法的信噪比明显高于FFT方法,较高的信噪比对于信号检测非常有利。随着Burg算法模型阶数的提高,信号的分辨率也逐渐提高,但是当阶数过低([p=5])时分辨率较低,造成漏警率较高;阶数过高([p=100])时容易出现谱峰分裂,出现大量虚假谱峰,无法正确判断车辆,造成虚警率和漏警率都很高。频谱特征如图10所示,在12和27频点存在两辆车。综合考虑信噪比、虚警率、漏警率和处理时间,采用[p=25]阶的Burg模型算法获取车辆时频信息。
[漏警率=CFAR漏检车辆数实际车辆数] (19)
[虚警率=CFAR多检车辆数实际车辆数] (20)
4.2 基于小波降噪的时频信号互相关算法验证
由于不同的分解层次对信号降噪效果有着直接的影响,当噪声较大时,目标车辆的时频信号信噪比较低,利用本文提出的基于信号分解层次的阈值函数降噪时,能准确地重构信号,如图11所示。
定义测速准确率为:
[δ=1-v-vv×100%] (21)
式中:[v]是车辆的真实速度;[v]是计算出的速度。
在不同小波基的作用下,测速结果表现不一样。基于coif小波降噪的时频信号互相关性具有很好的估计精度,测速准确率达到96%以上,如图12所示。
为验证基于小波降噪的时频信号互相关算法的准确率,利用实测数据对比时域信号互相关算法和未经过小波降噪的时频信号互相关算法,如表2所示。通过对比可以发现,在实测信号中由于地面杂波干扰较大,时域信号互相关算法并不能估计出实际车速,而时频信号互相关算法能估计出实际车速。未经过小波降噪的时频信号互相关算法估计出的车速平均准确率为90.0%,均方误差为12.3。基于小波降噪的时频信号互相关算法的测速平均准确率为96.7%,均方误差为7.96。可见,基于小波降噪的时频信号互相关算法的测速准确率较高,且鲁棒性较好。
4.3 算法整体验证
考虑到国内该类产品仍处于研发阶段并涉及商业机密,关于FMCW体制的双波束车流量雷达精准测速的实际工程结果较少,因此将本文提出的CC?BWT和另外两种具有代表性的相位法和双谱法做对比。针对车速快、慢的不同场景,分别进行了10组数据的仿真,每组数据有50个车辆信息,求每组数据的测速准确率平均值,其结果如图13所示。
双谱法和相位法的估计精度低,本文算法有较好的稳定性,无论是车辆快速行驶还是慢速行驶,都能保证较高的测速准确率,均高于96%。
4.4 实际路测
测试设备:PC、雷达、相机、传输线等;测试地点:某城市道路。
测试步骤如下:
1) 将雷达安装于道路一侧,调整安装角度,使雷达照射区域与车道方向垂直,并连接相机和PC。
2) 通过上位机设置雷达参数。上位机界面如图14所示,分别为参数设置区、通信数据区、车道模拟区。
3) 将雷达调整为工作模式,对行驶的车辆进行抓拍和测速,并保存原始数据,抓拍照片和视频用于后续统计分析和校正。
4) 对不同车速情况下重复上述三个步骤。
表3中分为三组采集数据,可以看出不管是在车速较慢还是在车速较快的情况下,都能保证95%以上的正确统计率和96%以上的测速精度。
5 结 语
本文通过对车流量雷达信号特点的分析,提出基于小波降噪的时频信号互相关测速算法,改善了双波束车流量雷达车辆检测率低和测速精度不高的问题。通过系统仿真和实际道路测试,本车流量雷达对于不同速度场景下的测速准确率均能达到96%以上,算法鲁棒性好。这对于车流量交通雷达的推广应用具有很大的现实意义,能够更充分地帮助交通管理部门检测道路交通情况,推进我国智能交通系统的建设。
参考文献
[1] 陈红江,张浩,汤灏,等.双天线雷达测速仪的研发[J].中国测试,2017,43(6):75?78.
[2] 刘玉佩.基于自适应时延估计的管道漏水定位方法研究[D].呼和浩特:内蒙古大学,2018.
[3] 李晶,赵拥军,李东海.基于马尔科夫链蒙特卡罗的时延估计算法[J].物理学报,2014,63(13):67?73.
[4] 崔维嘉,张鹏,巴斌.基于循环匹配追踪的稀疏重构时延估计算法[J].电子与信息学报,2018,41:1?7.
[5] 齐小刚,袁列萍,刘丽芳.奇异值分解的HB加权广义互相关时延估计[J].信号处理,2018,34(10):1160?1168.
[6] 赵培焱,欧阳鑫信,鹏华峰.基于中国余数定理的跳频信号相时延估计方法[J].电子与信息学报,2018,40(3):656?662.
[7] 李昕.基于双通道DFRFT互谱法的Chirp信号时延估计[J].电子学报,2014,42(6):1068?1073.
[8] 郑恩明,陈新华,孙长瑜.基于频率方差加权的时延差估计方法[J].系统工程与电子技术,2014,36(2):224?229.
[9] 王元恺,肖泽龙,许建中,等.一种改进的FMCW雷达线性调频序列波形[J].电子学报,2017,45(6):1288?1293.
[10] 邢自然,朱冬晨,金星.一种多目标FMCW雷达的高效距离速度测量[J].电子学报,2016,44(9):2148?2157.
[11] 王栋梁,刘英.Burg最大熵及其在切削颤振研究中的应用[J].制造与机床,2017,5(19):103?106.
[12] 赵兴岗,郑岱堃,王守勇,等.一种基于AR模型的矩阵CFAR检测器[J].电子学报,2017,45(12):3019?3024.
[13] 严天峰,张宇,魏楠,等.基于小波降噪的稀疏傅里叶变换时延估计[J].测控技术,2018,37(7):101?105.
[14] 李衡,赵毅强,杨瑞霞,等.基于小波降噪数据预处理的硬件木马检测优化[J].计算机工程与应用,2017,53(1):49?53.
[15] 李遂意.基于双波束雷达传感器的车速检测技术[D].南京:南京理工大学,2013.
